动车组重联网络控制系统时延预测及补偿
2018-12-18刘洋李常贤陈龙
刘洋,李常贤,陈龙
动车组重联网络控制系统时延预测及补偿
刘洋1,李常贤2,陈龙3
(1. 大连交通大学 现代轨道交通研究院,辽宁 大连 116028; 2. 大连交通大学 动车运用与维护工程学院,辽宁 大连 116028; 3. 中车大连机车车辆有限公司,辽宁 大连 116022)
重联动车组之间利用UIC网关的过程数据编组传输监控数据,数据在重联通信网络上的传输时延影响重联控制的性能。针对这一问题,构建动车组重联网络控制系统简化模型,采用网络时延的自回归AR模型,通过Yule-walker参数自辨识算法根据历史数据对网络时延进行在线预测,同时利用快速隐式广义预测控制IGPC对预测的时延进行补偿。仿真实验结果表明,该方法具有较高的时延预测精度,且对网络时延有较好的补偿效果,可保证良好的控制效果。
动车组;重联网络控制;UIC网关;时延预测;隐式广义预测控制
目前,我国动车组重联控制网络主要有ARCNET和TCN 2种,其中TCN网络应用较广泛。UIC网关以TCN为基础,且符合UIC556标准,是实现动车组之间互通、互联和互操作的关键设备[1],有助于实现不同型号动车组间重联控制,重联控制网络的引入会产生网络传输时延,导致控制指令不能及时送达重联列车的受控设备,且受控设备的状态无法及时反馈,进而影响列车的控制性能,甚至引起控制系统的不稳定[2−3]。针对网络控制系统(Networked Control Systems,NCS)数据传输时延,王义等[4]采用Lyapunov分析法得出CAN总线网络控制系统工作的稳定域。刘玉卿[5]给出一种用马尔可夫链分析其竞争冲突概率的方法,得出一种面向MAC的Lonworks总线时延模型。Lee等[6]分析Profibus-DP总线协议及网络诱导时延的产生的原因,并以步进电机为研究对象设计模糊逻辑控制器。FENG等[7]分析Ethernet,ControlNet和DeviceNet网络的网络诱导时延的大小和特性,为采用控制策略解决时延问题奠定了基础。BU等[8−9]分析无线通信模式下,CBTC中延时、丢包对列控系统性能的影响。步兵等[10]在文献[8]和文献[9]基础上提出了消除传输时延对列控系统影响的改进措施。上述研究均未涉及动车组重联控制网络的领域,本文以基于UIC网关的重联动车组过程数据传输网络时延为研究对象,采用文献[2]中的AR模型,利用历史数据对NCS前向通道的时延进行在线预测,并设计快速隐式广义预测控制器补偿网络时延的影响。
1 重联网络控制系统模型
为了突出研究方法,利用2个UIC网关和2个MVB设备,构建动车组重联网络控制系统简化模型,如图1所示,并作如下假设[11]:


图1 动车组重联网络控制系统简化模型
2 时延预估器设计



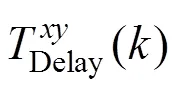
2.1 模型的定阶
利用Akaike信息准则(AIC)[12]来确定最佳阶次,以使系统的性能达到最佳。AIC准则函数为

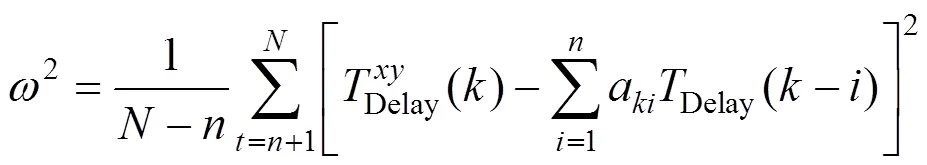
式中:时间序列样本数量为=1,…,,2为白噪声方差。
2.2 模型的参数估计
采用Yule-Walker方程法[13]根据新的时延值动态地调整加权系数a,在最小均方误差(MMSE)准则下,要使预测值最佳地逼近Delay(),参数a的选择应使

根据Yule-Walker方程
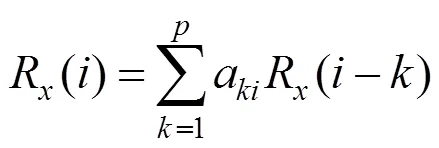
式中:R()为自回归时间序列的自相关系数。


3 时延补偿控制器设计
基于CARIMA模型[14],对象的离散差分方 程为:


选取如下性能指标函数进行滚动优化:


式中:为数学期望;0为最小预测长度,一般取0=;1为最大预测长度;N为控制长度;为加权系数;ref为参考轨迹;Δ为控制增量。
引入文献[15]中的Diophantine方程,得系统输出为:

式中:

欲使性能指标函数最小,需令:

则得使最小的控制律为:
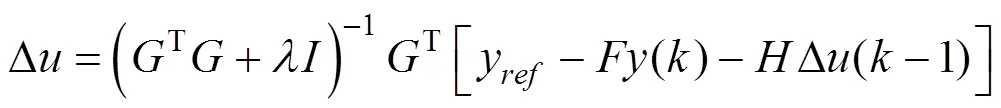
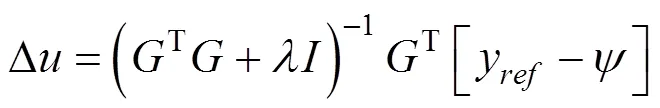
3.1 G的辨识
由式(10)和式(12)可得最后一个预测方程为



()可通过以下递推最小二乘公式估计为:


通过辨识出()的估计值*(),可求出矩阵中的各个元素。
3.2 ψ的辨识
根据GPC与DMC控制规律的等价性[16],可得预测输出为


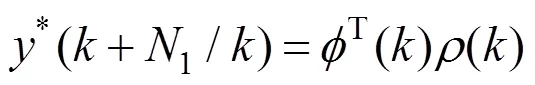
这样(+)就可通过式(17)计算
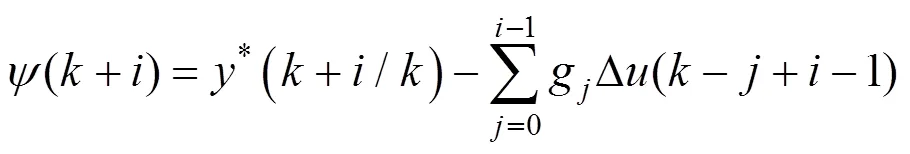

求得和,之后利用式(13)可计算控制量。则系统的广义预测控制律为

4 仿真实验与结果

根据图2,()准则曲线在阶数=7和=31附近取得2个较小值。理论上讲,当=31时,()取值最小,模型的适用度更高,但需要辨识的参数也越多,预测时间长。根据的不同取值,分别随机抽取2组样本进行预测,由图3和图4可以看出,预测时延和样本时延基本重合。故兼顾模型适用度和预测实时性,选取AR阶次为=7。
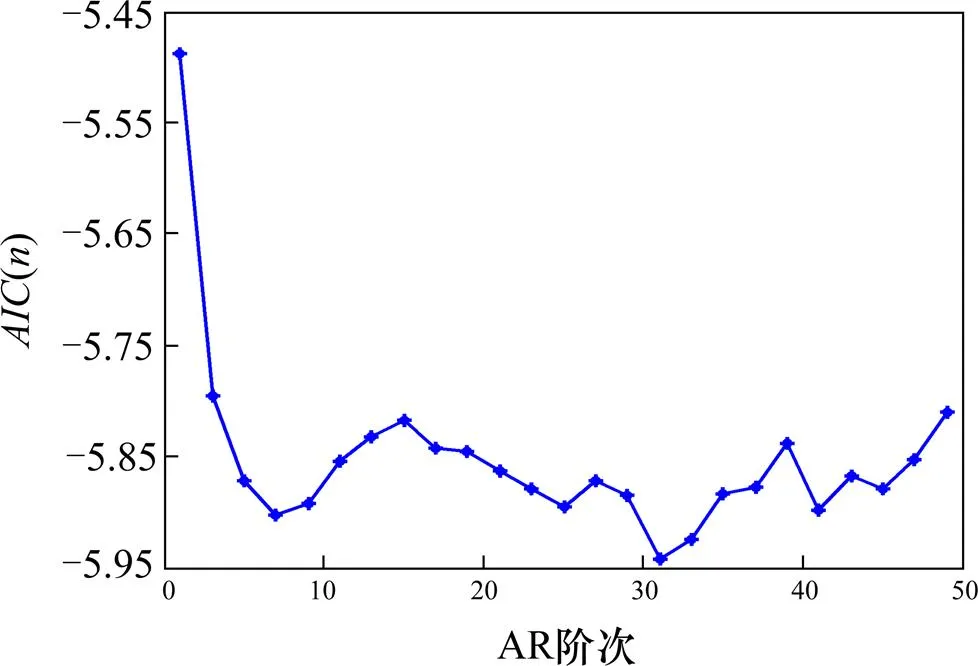
图2 AIC(n)准则曲线

(a) 第1组随机样本;(b) 第2组随机样本

(a) 第1组随机样本;(b) 第2组随机样本

图5 半实物仿真平台
为了验证时延补偿算法的有效性,针对动车组控制中常用的恒定值控制,取二阶系统()− 0.49(−1)=0.5(−2)+()/进行实验仿真。参数取T=0.1,1=6,=0.8,=1;系统初始值取g−1=1,(+)=1,0=105,其余初始值均为0。
从图6可以看出,在不存在网络时延的情况下,PID与IGPC二者的控制效果相当,甚至PID控制在超调量方面还略好于IGPC控制。但在存在网络时延的情况下,IGPC控制通过滚动优化和不断地在线辨识,有效地克服了模型失配造成的不利影响,使系统输出能够很好地跟踪控制输入参考轨迹,且系统响应时间短,超调量小,鲁棒性好。

(a);(b);(c);(d)
5 结论
1) 通过搭建半实物测试平台,采用往返时延RTT法对动车组重联控制网络中过程数据传输时延进行测量,测量结果表明:该网络时延在一定范围内随机分布。
2) 针对动车组重联网络控制系统中存在的网络时延,采用基于自回归AR模型的预测方法,利用历史时延预测当前时刻时延,具有较高的预测精度。
3) 针对动车组控制中常用的恒定值控制,采用快速广义预测控制算法对预测的网络时延进行补偿,系统输出很好地跟踪输入参考设定值,控制效果良好。本方法可为动车组网络控制时延研究提供理论支持。
[1] 李常贤, 刘洋, 张彤, 等. 用于动车组间互联、互通和互操作的UIC网关研究[J]. 中国铁道科学, 2013, 34(6): 110−116. LI Changxian, LIU Yang, ZHANG Tong, et al. Research on UIC gateway used for interconnection, intercommunication and interoperability between EMUs [J]. China Railway Science, 2013, 34(6): 110−116.
[2] 时维国, 邵诚, 孙正阳. 基于AR模型时延预测的改进GPC网络控制算法[J].控制与决策, 2012, 27(3): 477−480. SHI Weiguo, SHAO Cheng, SUN Zhengyang. Improved GPC network-control algorithm based on AR model time-delay prediction[J]. Control and Decision, 2012, 27(3): 477−480.
[3] 王军, 夏利民. 基于观测器的列车网络控制[J]. 铁道科学与工程学报, 2015, 12(5): 1205−1211. WANG Jun, XIA Limin. Train networked control based on observer[J]. Journal of Railway Science and Engineering, 2015, 12(5): 1205−1211.
[4] 王义, 何立仁. CAN总线时延网络控制系统稳定性研究[J]. 中北大学学报(自然科学版), 2014, 35(2): 132− 172. WANG Yi, HE Liren. Research of stability for CAN bus delay NCS[J]. Journal of North University of China (Natural Science Edition), 2014, 35(2): 132−172.
[5] 刘玉卿. 基于Lon总线的时延分析与实验平台研究[D].南京: 南京理工大学, 2009. LIU Yuqing. Time-delay analysis and study on experimental platform based on LON bus[D]. Nanjing: Nanjing University of Science & Technology, 2009.
[6] Lee K C, Lee S, Lee M H. Remote fuzzy logic control of networked control system via profibus-DP[J]. IEEE Transactions on Industrial Electronics, 2003, 50(4): 784−792.
[7] FENG L L, James R M, Dawm M T. Performance evaluation of control networks: Ethernet, controlnet, and devicenet[J]. IEEE Control Systems Magazine, 2001, 2(1): 66−83.
[8] BU Bing, YU F Richard, TANG Tao, et al. Performance improvements of communication-based train control (CBTC) systems with unreliable wireless networks[J]. Wireless Networks, 2014, 20(1): 53−71.
[9] BU Bing, YU F Richard, TANG Tao. Performance improved method for communication-based train control systems with random packet drops[J]. IEEE Transaction on Intelligent Transportation Systems, 2014, 15(3): 1179−1192.
[10] 步兵, 唐涛. 传输时延对CBCT影响的分析及消除[J].铁道学报, 2014, 36(6): 41−46. BU Bing, TANG Tao. Analysis and elimination of the impact of transmission delays on CBTC[J]. Journal of the China Railway Society, 2014, 36(6): 41−46.
[11] LIAN F L, Moyue J R, Tibury D M. Network design consideration for distributed control systems[J]. IEEE Trans on Contr Syst Tech, 2002, 10(2): 297−307.
[12] 杨绿溪. 现代数字信号处理[M]. 北京: 科学出版社, 2007: 212−220. YANG Lüxi. Modern digital signal processing[M]. Beijing: Science Press, 2007: 212−220.
[13] 常学将,刘维奇. AR模型识别及其参数的高阶Yule- Walker估计[J]. 应用数学学报, 1989, 12(2): 218−227. CHANG Xuejiang, LIU Weiqi. AR model identification and the high order Yule-Walker estimation of Autoregressive parameters[J]. ACTA Mathematicae Applicaitae Sinica, 1989, 12(2): 218−227.
[14] 吴密密, 戴文战. 基于改进粒子群算法的约束隐式广义预测控制[J]. 浙江理工大学学报(自然科学版), 2014, 31(3): 301−305. WU Mimi, DAI Wenzhan. A kind of constrained implicit generalized predictive control based on improved particle swarm optimization[J]. Journal of Zhejiang Sci-Tech University (Natural Sciences), 2015, 31(3): 301−305.
[15] 吴凡, 陈在平.广义预测算法在网络控制系统中的应用[J]. 天津理工大学学报, 2010, 26(1): 32−34. WU Fan, CHEN Zaiping. The application of generalized predictive control theory in networked control system[J]. Journal of Tianjin University of Technology, 2010, 26(1): 32−34.
[16] WANG Wei. A direct adaptive generalized predictive control algorithm with guaranteed stability[J]. Adaptive Control and Signal Processing, 1994, 8(3): 211−227.
(编辑 阳丽霞)
Time-delay prediction and compensation of EMU coupling network control system
LIU Yang1, LI Changxian2, CHEN Long3
(1. Mordern Railway Transportation Research Institute, Dalian Jiaotong University, Dalian 116028, China; 2. School of EMU Application and Maintenance Engineering, Dalian Jiaotong University, Dalian 116028, China; 3. CRRC Dalian Co., Ltd, Dalian 116022, China)
UIC gateway uses its function of process data marshalling to transmit control and monitoring data between coupling EMUs. There will be time-delay in the process of monitoring data transmission on the train coupling communication network. The network time-delay can deteriorate the coupling control performance. In order to solve this problem, simplified model of networked control system was established with respect to coupling EMU. The time-delay auto regressive (AR) model was established, and Yule-walker parameter self-identification algorithm was used for time-delay online prediction according to historical data. At the same time, fast implicit generalized prediction control was used for compensating predictive time-delay. Simulation results show that this method has high prediction accuracy, a good effect on time-delay compensation and can ensure the good control effect.
EMU; coupling network control; UIC gateway; time-delay prediction; implicit generalized predictive control
10.19713/j.cnki.43−1423/u.2018.12.004
U258.4;TP273
A
1672 − 7029(2018)12 − 3044 − 06
2017−11−23
中国铁路总公司科技研究开发计划项目(2015J007-D)
刘洋(1982−),男,吉林长春人,讲师,博士,从事轨道列车网络控制系统研究;E−mail:liuyang_82@163.com
