基于虚拟稳态同步阻抗的VSG输出阻抗与小信号建模分析

李 明 ，张 兴 ，张 行 ，张海峥 ，管玮琦 ，赵 为

（1.合肥工业大学电气与自动化工程学院，合肥230009；2.阳光电源股份有限公司，合肥 230088）

随着分布式新能源发电系统的迅速发展和渗透率的不断提高，传统电网呈现出电压和频率支撑能力变弱、惯性和阻尼特性缺失等特征。而虚拟同步发电机VSG（virtual synchronous generator）技术是一种将并网逆变器模拟出同步发电机特性的控制策略，目前已成为新能源发电领域的研究热点[1-5]。

通常而言，VSG是通过下垂控制来实现对输出频率和电压的调节，存在有功功率和无功功率易发生耦合振荡等问题[6]。一般VSG能有效运行的基本要求是传输线路接近纯感性，并且需满足小功角近似条件，但VSG技术通常都存在有功功率和无功功率耦合振荡的问题[7-8]。实际应用中，低压输电线路通常呈现阻感特性，VSG的有功功率和无功功率之间就会存在严重耦合，并且通常表现为欠阻尼振荡，使得功率动态调节过程有较大的超调量与调节时间，甚至使VSG无法控制并导致功率振荡发散[9]。针对该问题，通常的解决思路是对VSG的有功功率和无功功率进行解耦控制，大量文献对此进行了相关的分析。文献[10]提出虚拟功率控制策略，通过引入与线路阻抗相关的变换矩阵，实现了虚拟功率的解耦控制，但是逆变器实际输出的有功功率和无功功率仍然存在耦合现象；基于文献[10]，文献[11]进一步通过引入变换矩阵的方式，采用虚拟频率与虚拟电压，以实现实际输出功率的解耦。不同于上述文献，有功和无功功率解耦控制的另一类方法是虚拟阻抗技术[12-14]，通过虚拟电感、虚拟电阻、虚拟负阻抗等方式改变VSG的输出阻抗，以实现功率解耦。值得一提的是，虚拟稳态同步阻抗方案[15-16]是一种可通过调整逆变器输出阻抗特性，从而抑制功率振荡的典型虚拟阻抗技术方案。文献[15]提出了松弛小功角约束条件的VSG功率解耦方法，实现了更加精确的功率解耦，并对虚拟稳态同步阻抗方案的输出阻抗进行了分析，然而并未涉及虚拟稳态同步阻抗如何影响系统稳定性和阻尼特性的问题；文献[16]则通过虚拟稳态同步阻抗方案解决了逆变器输出电压不平衡问题，但是并没有给出该方案能够灵活设置输出阻抗特性的原因及其稳定性分析。本文在文献[15-16]的研究基础上，系统分析介绍了虚拟稳态同步阻抗方案影响VSG输出阻抗，并通过小信号模型阐述了虚拟稳态同步阻抗如何影响VSG系统稳定性和阻尼特性。

首先，本文介绍了基于虚拟稳态同步阻抗的VSG控制策略基本原理，分析了该方案的VSG输出阻抗特性，指出该方案下的输出阻抗可由设定的虚拟阻抗决定，与逆变器自身的滤波器和闭环控制器等参数无关。然后，通过建立逆变器小信号模型，得出了虚拟稳态同步阻抗可以增加系统低频域特征根阻尼比，有效抑制VSG输出功率耦合振荡的结论。最后，本文结合Matlab/Simulink仿真和实验，进一步验证了基于虚拟稳态同步阻抗的VSG控制策略理论分析的正确性。

1 基于虚拟稳态同步阻抗的VSG控制策略

基于VSG控制策略的并网逆变器示意如图1所示。

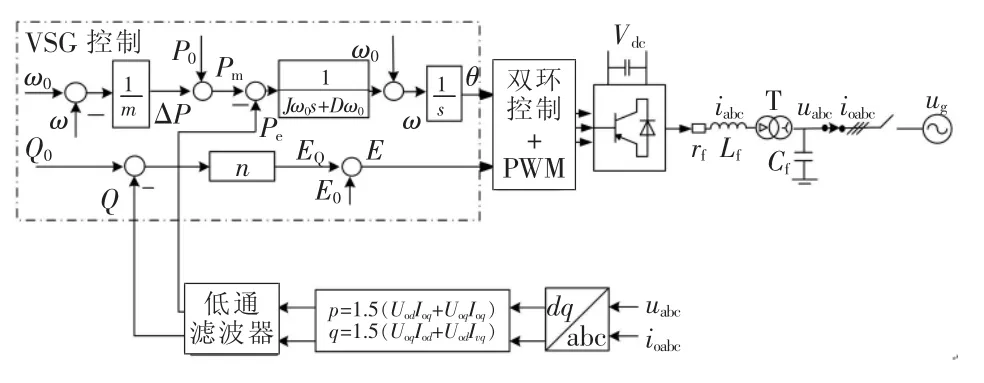
图1 基于VSG控制策略的并网逆变器示意Fig.1 Schematic of grid-connected inverter based on VSG control strategy

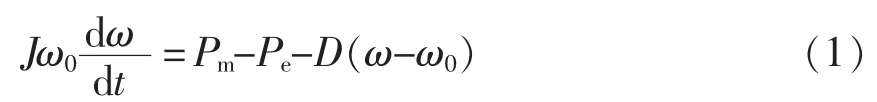
式中：J为VSG的虚拟转动惯量；Pm和Pe分别为VSG的机械功率和电磁功率；D为VSG的虚拟阻尼系数；ω0为同步角速度。

VSG的电磁方程表达式为

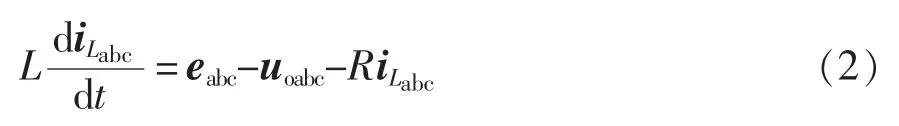
VSG的机械方程表达式为

式中：L为VSG的同步电抗；iLabc为VSG的电感电流；eabc为VSG的内电势；uoabc为VSG的输出电压；R为VSG的电枢电阻。

根据图1，VSG输出瞬时电磁功率pe为

式中：Uod、Uoq分别为VSG输出电压的d、q轴分量；Iod、Ioq分别为VSG输出电流的d、q轴分量。

通过一阶低通滤波器LPF（low pass filter）得到VSG的输出电磁功率Pe为

式中，τ为LPF的时间常数。

根据图1，VSG的输出机械功率Pm由两部分组成，即

式中：P0为VSG的有功给定值；m为有功功率调节系数。

VSG内电势的幅值E表达式为

式中：E0为VSG的空载电势；Q0为VSG的无功给定；n为无功功率调节系数；Q为VSG输出的平均无功功率，类似于VSG输出电磁功率，经过一个LPF输出平均无功功率，其表达式为

综合式（1）～式（7），构成了如图1所示的 VSG控制策略基本框图。

基于虚拟稳态同步阻抗的方案是一种有效的虚拟阻抗方案，能够改变并网逆变器的输出阻抗特性，以消除VSG的输出有功功率和无功功率的耦合。图2所示为采用基于虚拟稳态同步阻抗矩阵后的VSG控制策略具体框图。

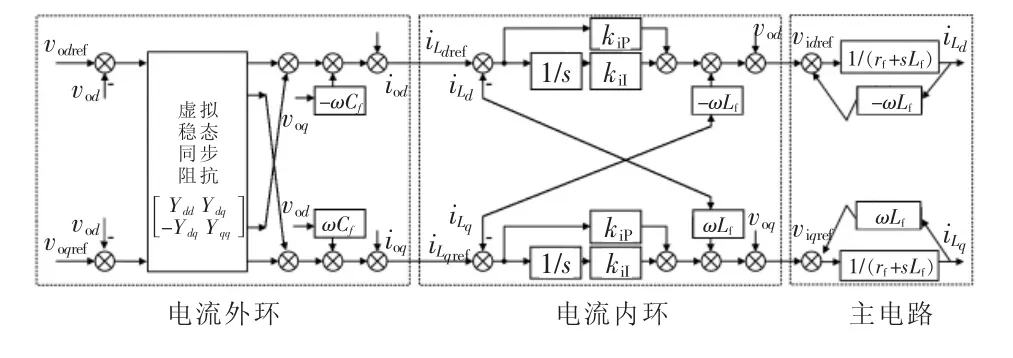
图2 虚拟稳态同步阻抗方案控制框图Fig.2 Control block diagram of virtual steady-state synchronous impedance scheme

2 基于虚拟稳态同步阻抗方案的VSG输出阻抗分析

由图2可见，虚拟稳态同步阻抗方案是：在两相旋转坐标系下，将经过坐标变换后的d轴和q轴分量vodref、voqref，以及实际采样的VSG输出电压d轴和q轴分量vd、vq，与虚拟稳态同步阻抗矩阵相乘之后得到电流内环指令值iLdref、iLqref。因此，虚拟稳态同步阻抗矩阵的表达式为

式中：Rv为虚拟稳态同步阻抗的阻性分量；Lv为虚拟稳态同步阻抗的感性分量。

根据图2，VSG的虚拟稳态同步阻抗矩阵构成的电压外环方程为

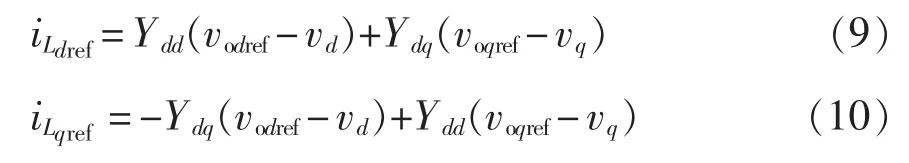
VSG的电流内环与主电路部分方程分别为

式中，kiP和kiI分别为电流内环PI调节器的比例系数与积分系数。

综合式（9）～式（12），得到 VSG 输出阻抗矩阵为

根据式（13），输出阻抗 Zout（s）在 s=0（即直流频率）时，仅与设置的虚拟稳态同步阻抗矩阵有关，而与VSG主电路滤波器和控制器等参数均无关。

另外，由于上述推导是在两相旋转坐标系下进行，通过坐标逆变换，直流频率对应于三相静止坐标系下的50 Hz频率。由此，VSG的工频50 Hz输出阻抗也是由设置的虚拟稳态同步阻抗矩阵决定，与VSG主电路滤波器和控制器等参数均无关，从而简化了VSG输出阻抗的设计。

进一步地，根据式（13），可得采用虚拟稳态同步阻抗控制时的逆变器等效输出阻抗Zdd（s）为

由式（14）可得采用虚拟稳态同步阻抗控制时的逆变器等效输出阻抗和实际物理阻抗特性的Zdd（s）的Bode图，如图3所示。

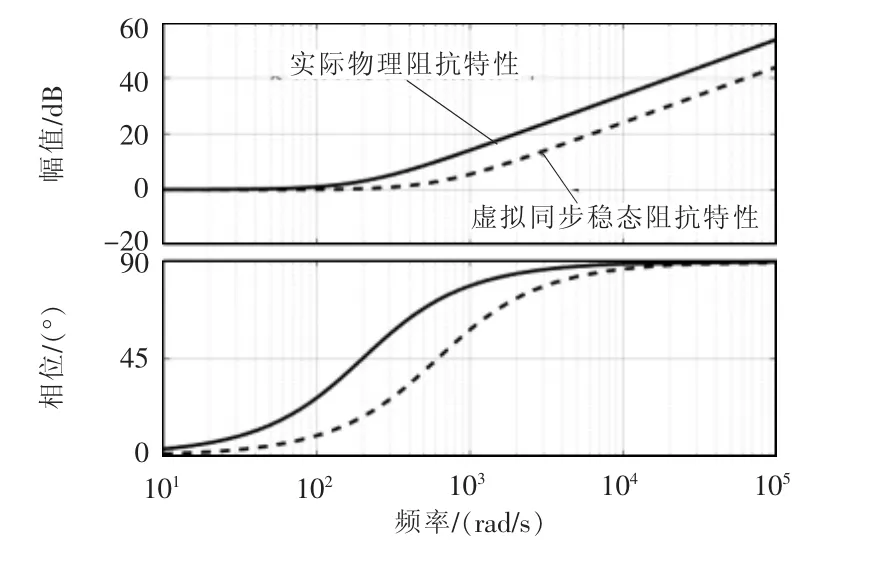
图3 采用虚拟稳态同步阻抗控制时的逆变器等效输出阻抗和实际物理阻抗特性的Zdd（s）的Bode图Fig.3 Bode diagram of Zdd（s）with equivalent output impedance and actual physical impedance characteristics of inverter under virtual steady-state synchronous impedance control

实际物理阻抗的电阻设置为1 Ω，电感设置为5 mH，虚拟稳态同步阻抗设置与实际物理阻抗大小一致。根据图3，低频附近的虚拟稳态同步阻抗和实际物理阻抗差异不大，因此VSG的工频50 Hz输出阻抗可由设置的虚拟稳态同步阻抗矩阵灵活设置决定；而在中高频附近，虚拟稳态同步阻抗幅值小于实际物理阻抗，但是相位保持了一致。因此虚拟稳态同步阻抗下的VSG抗高频扰动能力得到了一定的提升。

3 基于虚拟稳态同步阻抗的VSG小信号模型

本文第2节分析了采用虚拟稳态同步阻抗可灵活设置VSG的输出阻抗特性，因此只要如果VSG的输出阻抗呈现出感性特性，VSG的稳态特性就呈现出有功-频率（P-ω）和无功-电压（Q-E）的下垂控制特性，如式（5）式（6）所示。

在小信号扰动下，结合式（3）和式（5），可得

式中，kP为考虑VSG的虚拟阻尼系数时的等效P-ω下垂系数。而当VSG并网运行时，根据式（1）～式（7）可得

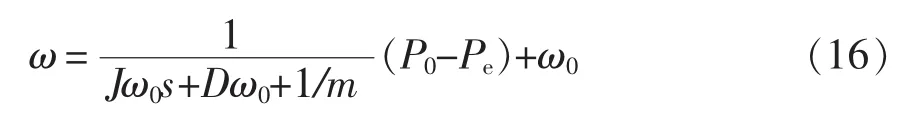
小信号扰动下，VSG的功率输出特性可为

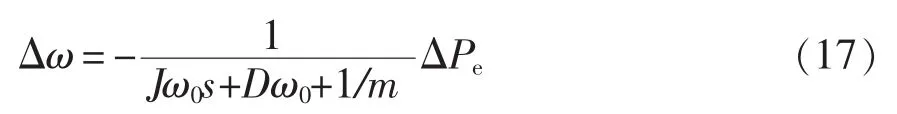
对比式（15）和式（17）可见，小信号扰动下的VSG与下垂控制的表达式形式类似。如果VSG的参数满足

则VSG与下垂控制具有相同的控制特性。基于上述分析，VSG是一种特定参数下的下垂控制[17]。因此，基于该结论，对采用虚拟稳态同步阻抗的VSG采用下垂控制进行等效建模分析。

图4所示为逆变器并网运行时的等效电路。图4中：Xv和Rv分别为通过虚拟稳态同步阻抗矩阵设置的输出电抗与电阻，Xv=sLv；δ为VSG的输出功角。

图4 逆变器并网时的等效电路Fig.4 Equivalent circuit of inverter in grid-connected mode

根据图4可得并网电流为

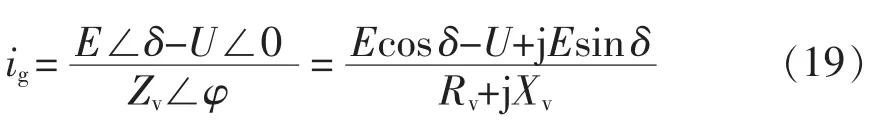
式中：U为电网电压幅值；ig为并网电流；Zv和φ分别为虚拟输出阻抗的幅值和相位。

为了应用VSG，设置虚拟稳态同步阻抗中的Rv=0时，仅保留感性阻抗分量。此时输出有功功率和无功功率为

将式（20）进行线性化处理，并结合式（15）得

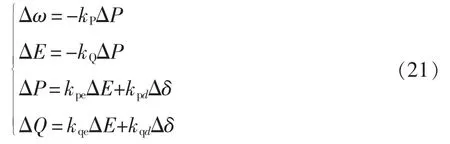
式中：kQ为考虑BSG的虚拟阻尼系数时等效Q-E下垂系数。式中其他系数可分别表示为

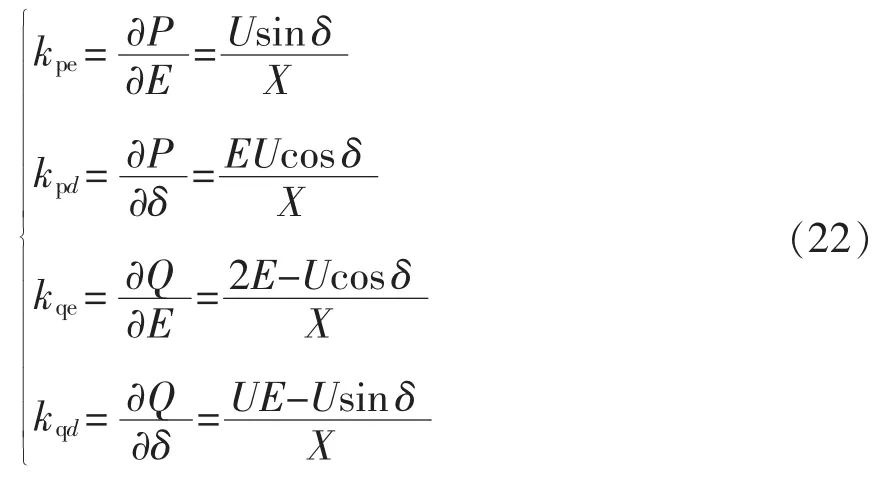
综合式（21）～式（23），得

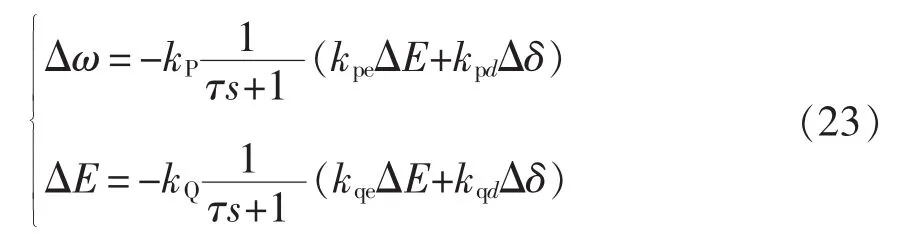
由于 Δω=sΔδ，因此由式（24）得到下垂控制的小信号闭环传递函数特征方程为

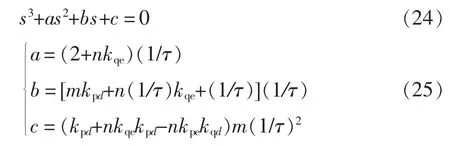
将式（18）代入式（25），则可得到 VSG 并网运行时小信号闭环传递函数特征方程的系数分别为

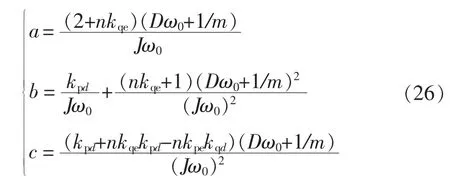
本文采用的参数为：ω0=314 rad/s，U=220 V，E=220 V，δ=0.01 rad。根据式（24）和式（26）可得当虚拟稳态同步电抗Xv从0.1 Ω变化至10 Ω时式（26）所示的闭环传递函数的根轨迹变化情况，如图5所示。

图5中，箭头方向为系统的闭环极点随虚拟稳态同步电抗Xv增大的变化趋势。可以看出，Xv增加，系统极点虚部减小，向实轴靠近，系统阻尼增加，超调减小，稳定性得到了一定程度地增强；但随着Xv的进一步增加，极点会逐渐向虚轴方向移动，从而稳定性会有所降低。因此，可以通过增加虚拟稳态同步电抗的方式来增大系统阻尼，但是不能过大。

图5 闭环传递函数的根轨迹变化情况Fig.5 Change in the root locus of closed-loop transfer function

4 仿真和实验

4.1 仿真验证

为了验证上述理论分析的正确性，利用Matlab/Simulink搭建了三相LCL型并网逆变器的仿真平台。当虚拟稳态电抗Xv=0.1 Ω时，首先1台100 kW并网逆变器以VSG模式带100 kW负载运行（记为1#VSG），在t0时刻切入另外1台以VSG模式的100 kW并网逆变器 （记为2#VSG），2台VSG的输出有功功率波形如图6所示。由图可见，当虚拟稳态阻抗较小时，2台VSG在功率均分过程中功率振荡过程明显，超调量较大。

工况与图6相同，图7给出了当虚拟稳态电抗Xv=10 Ω时的仿真波形。由图7可见，2台VSG在功率均分过程中，功率振荡过程得到了明显的抑制，没有超调量，呈现出较高的阻尼特性。该结论和图5相一致。

图6 Xv=0.1 Ω时2台VSG的输出功率均分过程仿真波形Fig.6 Simulation waveforms of output power equalization process of two VSGs with Xv=0.1 Ω

图7 Xv=10 Ω时2台VSG的输出功率均分过程仿真波形Fig.7 Simulation waveforms of output power equalization process of two VSGs with Xv=10 Ω

4.2 实验验证

为了验证本文对现有控制方案分析的正确性，搭建了如图8所示的实验平台。图中，1#和2#并网逆变器容量为100 kW，以VSG模式运行；直流源通过1台250 kW整流器实现。VSG和整流器均以DSP TMS28335进行控制。

设置实验工况与仿真工况完全一致。图9给出了虚拟稳态电抗Xv=0.1 Ω和10 Ω时2台VSG的输出功率均分过程实验波形。对比图6和图7可见，实验波形和仿真波形符合很好。

图8 实验平台照片Fig.8 Photo of experimental platform

图9 Xv=0.1 Ω和Xv=10 Ω时2台VSG的输出功率均分过程实验波形Fig.9 Experimental waveforms of output power equalization process of two VSGs with Xv=0.1 Ω and Xv=10 Ω

5 结论

本文介绍了基于虚拟稳态同步阻抗的VSG控制策略基本原理，并结合Matlab/Simulink仿真和实验，验证了基于虚拟稳态同步阻抗的VSG控制策略性能分析的正确性。结论如下：

（1）分析了该方案下的VSG输出阻抗特性，发现该方案下的输出阻抗可由设定的虚拟阻抗决定，与逆变器自身的滤波器和闭环控制器等参数无关。

（2）本文通过建立逆变器小信号模型，得出了虚拟稳态同步阻抗可以增加VSG系统低频域特征根阻尼比，有效抑制功率耦合振荡。