基于扩大搜索邻域A＊算法的平滑路径规划

2018-12-17张敬寒陶兆胜彭澎王丽华

长春理工大学学报（自然科学版） 2018年6期

张敬寒，陶兆胜，彭澎，王丽华

（安徽工业大学机械工程学院，马鞍山 243032）

路径规划[1]作为机器人的研究方向之一，一直是学者研究的热点。栅格法[2]将机器人运行环境特征信息转换为具有二值信息的单元网格存储，因其简便、易处理的特点在环境建模中具有显著优势。为此，学者基于栅格法研究了如 A*[3]、D*[4]和D*Lite[5]等算法，其中启发式搜索[6]A*算法因其简单高效、可操作性强和准确性高的特点而被广泛应用于解决静态全局路径规划问题。但A*算法受节点搜索策略影响，存在规划路径不是理论上的最优路径、路径拐点过多[7，8]，且当环境信息过于复杂时算法搜索效率降低的缺陷。

本文提出一种基于改进A*算法的平滑路径规划方法。首先，针对A*算法规划路径长度不是最优和路径拐点较多的不足，提出一种扩大算法搜索邻域的改进方法，消除了节点移动方向0.25π整数倍和8邻域搜索的限制；其次为提高算法寻路效率，利用最小二叉堆优化A*算法OPEN列表数据存储结构；最后采用三次均匀B样条曲线平滑处理，综合改进A*算法规划路径，以满足机器人运动时对速度和加速度连续性的实时要求。

1 A*算法基本理论

A*算法通过启发信息引导算法搜索下一待扩展节点，其估价函数为：

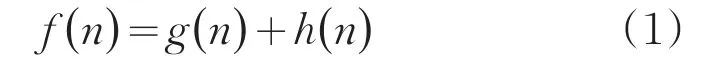
式中，g(n)为当前节点n与起始节点之间的移动代价；h(n)为当前节点n与目标节点之间的移动代价，即启发函数。

设机器人运行环境的目标节点为G，坐标为，则启发函数h(n)：

2 扩大搜索邻域A*算法

标准A*算法搜索下一待扩展节点采用8领域算法，如图1所示。每个搜索方向之间夹角均为0.25π，节点转折角为0.25π的整数倍，为此标准A*算法的规划路径距离不是最短，且规划路径上因转折点较多不够平滑。

图1 8邻域搜索示意图

为消除8邻域搜索缺陷，本文提出扩大A*算法当前节点搜索邻域范围的改进算法。以图1中7×7无障碍物栅格地图为例，中心节点为当前节点n，其周围第一层8个节点为标准A*算法待扩展节点。本文算法除了采用8领域搜索算法外，还将当前节点n周围第二层16个节点（如图2所示）纳入算法下一步待扩展节点，此时算法待搜索邻域节点数为24个，节点移动方向为16个方向。以此类推，A*算法的可扩展搜索邻域节点和可移动方向个数随着搜索层数的扩展一直增加，如图3所示。

设R表示由当前节点n搜索下一节点时待扩展的节点层数，NR表示待搜索邻域节点个数，SR表示随节点可移动方向个数，则：

式中，R≥1,R∈Z。

图2 24邻域搜索示意图

图3 48邻域搜索邻域示意图

由此得到与R取值对应的不同NR和SR值，如表1所示。

表1 搜索层数与待搜索邻域个数和可移动方向的对应关系

3 最小二叉堆优化A*算法OPEN列表

本文提出的扩大搜索邻域算法导致OPEN列表中待搜索节点数量增多，数据存储标记更加复杂，严重影响算法效率。为此利用最小二叉堆优化OPEN列表节点存储方式。图4所示为典型的最小二叉堆：键值最小点在堆的顶端，并存储在一维数组的首位，其子节点的键值均高于该节点，分别存储在数组的2和3位置，以此类推。

图4 最小二叉堆及其数据存储

最小二叉堆的堆序特性保证OPEN列表节点排列的稳定性，算法搜索OPEN列表中估价函数f(n)值最小节点的时间复杂度为O(1)[9-10]。

4 A*改进算法的路径规划

4.1 环境建模

本文采用直角坐标法标记栅格环境信息，以每个栅格的中心点坐标表示整个栅格信息。设置栅格粒度值为1，坐标系原点坐标（0.5，0.5），即所有栅格中心点横、纵坐标均为整数。图5所示的30×30大小仿真实验地图以课题组实验室环境为模型建立。

图5 实验室环境建模地图

4.2 仿真实验

本文算法的代码编写和仿真均在Windows8 64位系统Matlab2013b软件中实现。

（1）标准A*算法、24邻域A*算法和48邻域A*算法对图5环境的路径规划仿真实验结果分别如图6、图7和图8所示，每组重复仿真10次，记录每次路径规划的时间ti和规划路径包括的节点个数及其坐标，并计算路径长度。

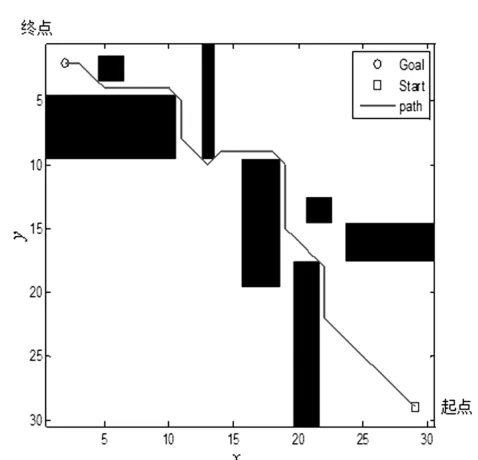
图6 标准A＊算法

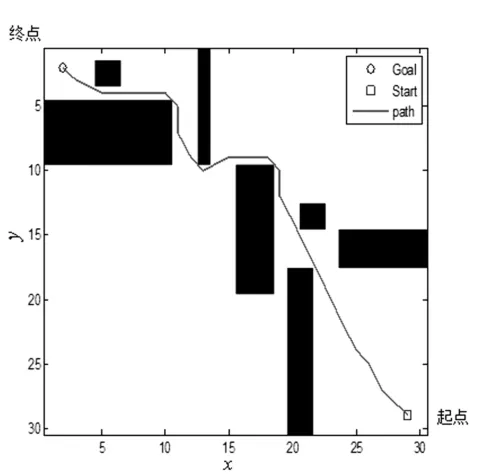
图7 24邻域

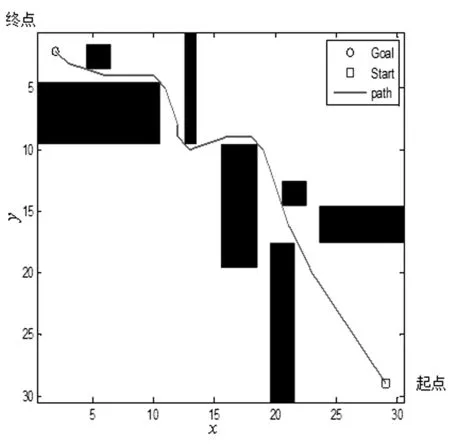
图8 48邻域

（2）最小二叉堆优化OPEN列表后的8邻域、24邻域和48邻域A*算法对图5环境的路径规划仿真实验结果分别如图9、图10和图11所示，每组重复仿真10次，记录每次路径规划的时间ti和规划路径包括的节点个数及其坐标，并计算路径长度。

本文提出的算法规划路径节点个数、长度和时间代价如表2所示。

图9 二叉堆标准A＊算法

图10 二叉堆24邻域

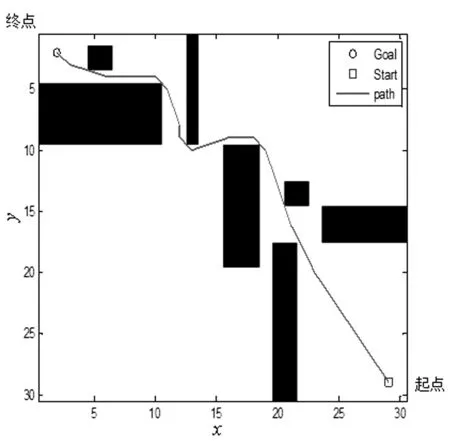
图11 二叉堆48邻域

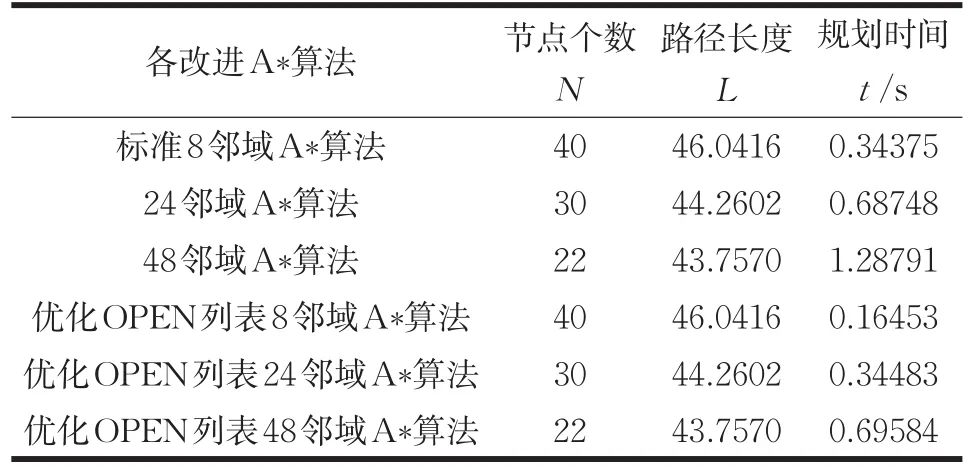
表2 算法性能对比

通过表2和图6、图7、图8可知24邻域和48邻域的改进A*算法相对于标准A*算法：（1）规划路径上节点个数依次降低，分别为40、30和22；规划路径距离即移动代价逐渐减小，路径渐为平滑；（2）路径规划效率不断降低，时间代价依次增加了0.34373s和0.94416s，算法效率降低。

通过表2和图6与图9、图7与图10、图8与图11可知：（1）最小二叉堆不影响A*算法的节点选择策略，优化OPEN列表前后算法规划路径完全一致；（2）最小二叉堆优化OPEN列表使得8邻域、24邻域和48邻域A*算法路径规划并的平均时间分别降低了47.86%、49.84%和45.97%，有效改善因搜索邻域扩大导致算法路径规划时间增加的不足，算法效率显著提高，提高了路径规划实时性。

5 三次均匀B样条曲线平滑路径

本文提出的扩大搜索邻域A*算法虽然在一定程度上平滑了路径，但依然存在部分路径区域转折角度过大，路径尖峰。机器人实际移动时突然转向加减速会损害伺服电机和齿轮，并不易追踪规划路径[11]。而具有分段多项式形式的B样条曲线因其参数及表达式简单、凸包性及局部修改性等优点而广泛应用于路径平滑处理[12]。其中三次B样条曲线在节点矢量处二阶连续[13-14]满足对于机器人速度和加速度连续性的要求，故本文采用三次均匀B样条曲线平滑综合改进上述本文算法已规划的路径。

5.1 三次均匀B样条曲线方程

设n+1个顶点Pi(i=0,1,…,n)构成的特征多边形，则k次（k+1阶）的B样条曲线表达式[15]：

令Ni,k(u)称为基函数，则：

式中，0≤u≤1,i=0,1,…,k-1

由公式（4）可知当k=3时，三次均匀B样条曲线的数学表达式为：

三次均匀B样条曲线的基函数数学表达式为：

将公式（8）上式带回公式（4）得三次均匀B样条曲线：

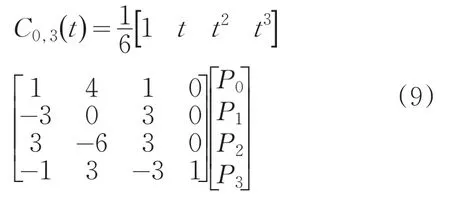
5.2 仿真实验

三次均匀B样条曲线平滑综合改进24邻域A*算法规划路径（图7）的仿真结果如图12所示，放大节点（19，10）和（18，9）处区域如图12所示，因篇幅关系其余区域放大图并未贴出，通过对比可知三次均匀B样条曲线消除了原规划路径上节点（19，10）、（18，9）、（13，10）、（12，9）、（11，7）、（11，5）、（11，4）处的路径尖峰点，平滑后的路径由平滑连续的曲线组成，有利于机器人移动时保持速度与加速度的连续性。