高考函数审题易错点总结
2018-12-17耿海艳
耿海艳
(武功县普集高级中学 陕西咸阳 712200)
一、易错点:用错恒成立的条件
例1.已知函数f(x)=x2+ax+3-a若x∈[-2,2]时,f(x)≥0恒成立,求a的取值范围.
错解一:∵f(x)≥0恒成立,∴△=a2-4(3-a)≤0恒成立解得a的取值范围为-6≤a≤2;
错解二:∵f(x)=x2+ax+3-a若x∈[-2,2]时,f(x)≥0恒成立,
错因:对二次函数f(x)=ax2+bx+c当x∈R上f(x)≥0恒成立时,△≤0”片面理解为“ax2+bx+c≥0,x∈[-2,2]恒成立时,△≤0”;
二、易错点:函数单调性考虑不周致误
错解:(-∞,1)∪(1,+∞)
错因分析:忽视了函数在定义域分界点上函数值的大小.
易错突破:分段函数的单调性不仅要使函数在各个段上具有单调性,还要考虑分界点上函数值大小.
三、易错点:混淆“过点”与“切点”致误
例3.求过曲线y=x3-2x上的点(1,-1)的切线方程.
错解:∵y'=3x3-2,∴k=y'|x=1=3×12-2=1,
∴切线方程为:y+1=x-1,即x-y-2=0.
错因分析:混淆“过某一点”的切线和“在某一点处”的切线,错把(1,-1)当做切点.
正解:设P(x0,y0)为切点,则切线的斜率为
解得x0=1,或x0=,故所求切线方程为y-(1-2)=(3-2)(x-1)。
易错突破:过曲线上的点(1,-1)的切线与曲线的切点可能是(1,-1),也可能不是(1,-1).本题错误的根本原因就是把(1,-1)当成了切点.解决这类题目时,一定要注意区分“过点A的切线方程”与“在点A处的切线方程”的不同.虽只有一字之差,意义完全不同,“在”说明这点就是切点,“过”只说明切线过这个点,这个点不一定是切点.
四、易错点:函数极值点概念不清致误
例4.已知f(x)=x3+ax2+bx+a2在x=1处有极值为10,则a+b=______.
错解:-7或0。
错因分析:忽视了条件的等价性,“f'(1)=0”是“x=1为f(x)的极值点”的必要不充分条件。
正解:f'(x)=3x2+2ax+b,由x=1时,函数取得极值10,
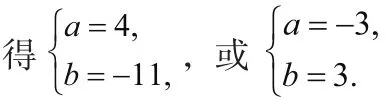
当a=4,b=-11时,f'(x)=3x2+8x-11=(3x+11)(x-1)在x=1两 侧 的 符号相反,符合题意。
当a=-3,b=3时,f'(x)=3(x-1)2在x=1两侧的符号相同,所以a=-3,b=3不符合题意,舍去。
综上可知a=4,b=-11,∴a+b=-7。
易错突破 :对于可导函数f(x):x0是极值点的充要条件是在x0点两侧导数异号,即f'(x)在方程f'(x)=0的根x0的左右的符号:“左正右负”⇔f(x)在x0处取极大值;“左负右正”⇔f(x)在x0处取极小值,而不仅是f'(x0)=0.f'(x0)=0是x0为极值点的必要而不充分条件.对于给出函数极大(小)值的条件,一定要既考虑f'(x0)=0,又考虑检验“左正右负”或“左负右正”,防止产生增根.
总之,不要急于攻难度大的“综合题、探究题”,不要盲目地自己找题。精做题,审好题,才能做好题。要在解题的过程中,适时进行探究式、开放式题目的方法总结。明确自己在解题过程中运用到的知识点和整个解题思路。并加以自觉的应用。这样每做一题在解题方式和思路上,都获得积累。复习要真正地回到重视基础的轨道上来,搞清基本原理、基本方法,体验知识形成过程以及对知识本质意义的理解与感悟,同时,对基础知识进行全面回顾,并形成自己的知识体系。
