正弦型函数图像的变换及其应用
2018-12-15
(华中科技大学附属中学高三(4)班 湖北武汉 430000)
一、函数y=Asin(ωx+φ)图像的变换
函数y=Asin(ωx+φ)(其中A,ω,φ都是常数,且A>0,ω>0)是一种重要的三角函数模型,由正弦函数y=Asin(ωx+φ)(A>0,ω>0)的图像,由两种变换途径:“先平移后伸缩”与“先伸缩后平移”,其变换规律是:
1.先平移后伸缩
(1)相位变换(平移变换)。将函数y=sinx的图像沿x轴向左平移φ(φ>0)个单位,或向右平移丨φ丨(φ>0)个单位,得到函数y=sin(x+φ)的图像。
(2)周期变换。将函数y=sin(ωx+φ)图像的纵坐标不变,横坐标变为原来得到y=sin(ωx+φ)的图像。
(3)振幅变换。将函数y=sin(ωx+φ)图像的横坐标不变,纵坐标变为原来的A倍,得到y=Asin(ωx+φ)的图像。
2.先伸缩后平移
(1)周期变换。将函数y=sinx的图像纵坐标不变,横坐标变为原来的得到y=sinωx的图像。
(2)相位变换(平移变换)。将函数y=sinωx的图像向左(φ>0)或向右(φ<0)平移丨丨个单位,得到y=sin(ωx+φ)的图像。
(3)周期变换。将函数y=sin(ωx+φ)图像的横坐标不变,纵坐标变为原来的A倍,得到y=sin(ωx+φ)的图像。
二、应用
1.由图像写出与之对应的函数y=Asin(ωx+φ)(A>0,ω>0)的解析式,其中关键的确定A,ω和φ的值。A通常由最大值和最小值确定,即最大值减最小值除以2;ω由周期确定:而(这里的x0是指用“五点法”作图时的起点横坐标),或者是将图像上的点的坐标代入,借助待定系数法求解。
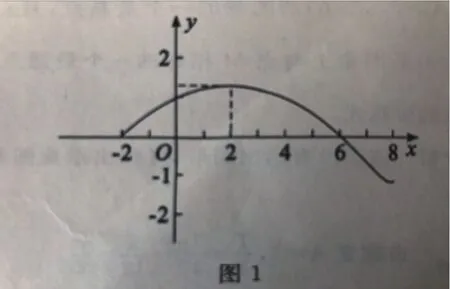
分析 虽然是部分图形,但也能反应出函数的特征。
点评 (1)由函数y=Asin(ωx+φ)(A>0,ω>0)的一段图像,求此函数的表达式,其表达式往往不唯一,要根据具体问题具体分析,这类问题中,A比较容易求,困难的是求ω和φ。一般地,由图像定周期,由周期求出ω;确定φ时,通常从图像上看清五个关键点在什么地方,应该是五点作图法中的第几点,通过ωx+φ即可求出φ。如上例中,注意(—2,0)是五点作图时的第一个点,所以ωx+φ=0,其中x=—2,可知再如,是五点作图法的第二个点,所以ωx+其中x=2,可知若对A,ω或φ范围有要求,可用诱导公式变换,使其符合要求。
(2)、如果题目不给出图形,可以根据条件画出示意图,再用待定系数法求解。
分析 该题目没有给出图形,可画出示意图帮助理解。