应用Copula函数的潘家口水库设计洪水线推求

喀迪尔·麦麦提

（新疆英吉沙县水利局，新疆 英吉沙 844500）

0 引言

洪水过程线随机模拟是水利工程防洪设计的关键内容，也是水利安全、洪水灾害控制的依据[1]。此前防洪设计中以传统单变量倍比放大或同频率设计方案为主，虽然其操作流程简易、各特征量重现周期易于满足防洪标准，但仍需要指出的是存在明显局限性：①单纯考虑洪水特征量，忽视了期间非线性、相关性关系[2]；②将防洪安全标准与设计洪水过程线的特征量的频率等同考虑，避开了洪水过程联动性等水文规律[3]。随着计算科学的发展，国内外学者提出了自回归[4]、多元统计[5]、典型解集模型[6]、神经网络[7]等模型应用于洪水过程随机模拟，然而未能有效识别变量间共线性、依存关系，且难以实现多维变量联合分布分析。Copula函数能够联立多变量间复杂关系，其边缘分布灵活多样，在水文研究中取得良好应用。高超等[8]运用用三维Copula函数以构建洪水特征量联合分布模型，并探究了洪水过程线形状和三维对称型Archimedean Copula函数公式对模拟精度的影响；刘和昌等[9]构建了基于Copula函数的洪峰、洪量之间的函数关系，由此计算了峰量的边缘分布频率；李天元等[10]以隔延河水库为例，对比分析了单变量同频与多变量同频洪水过程线设计的差异，结果表明，基于Copula函数构造的联合分布模型由于传统同倍比方法。鉴于此，本文以二维Copula函数为基础理论建立潘家口水库峰量的联合分布，并推求设计洪水，以期为水库安全管理提供基础信息。

1 原理与方法

1.1 Copula函数原理

Copula函数是基于多元分布理论而将联合分布函数与边缘分布函数连接构建的一种相依性测度方法，对于传统共线性问题不能准确识别变量间相依信息，Copula能够排除这些高度相关影响，以构造二维离散分布模型进行随机模拟。Nelsen[11]将N元Copula函数定义域设定为[0～1]；其在洪水过程线模拟的应用通常以1、2、3维度为主，本研究采样双变量同频率设计方案，故针对二维Copula函数表达如下[12]：

式中：C 为 Copula 函数，U1(x1)，U2(x2)，…，Un(xn)在区间是连续分布的；则其相应的联合概率密度函数表示如下：

式中：u=FX(x),v=FY(x)分别代表分别为随机变量X、Y的边缘分布函数。洪水过程是洪峰、时段等特征量的函数，具有多元、非线性特征，因而二维变量联合分布模拟多以Archimedean Copula函数函数簇应用较多，且适应性强，其能够纠正共线性情形，辨识上尾相关性，其公式如下：

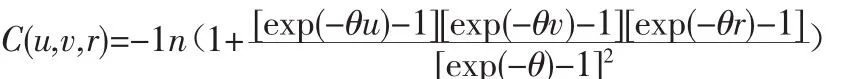
式中：u、v、r均为边际分布函数，θ为Copula函数的参数。其密度函数为：

函数参数θ与Kendall秩相关系数τ关系表示如下：

1.2 边缘分布频率

洪峰、洪量是洪水过程的矢量之一，其随时间变化符合PIII分布。已知洪峰Q、洪量W的分布函数为[13]：

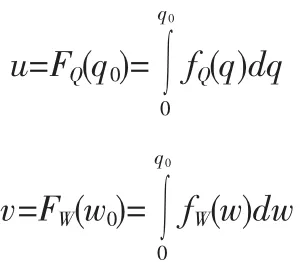
式中：q0、w0分别表示洪峰、时段洪量给定值；a、β、a0依次为形状、尺度、位置参数，其用于度量洪水特征。根据边缘分布概率定理；则其二维离散型频率计算公式如下：

式中：T为伽马函数。

1.3 推求设计洪水过程线

以洪峰、洪量、洪水历时等特征量构建Copula联合分布函数进行联合模拟，以描述洪水过程。基于Copula函数，在指定洪水历时条件下，其分布如下[14]：

上式可转化为：

假设Copula函数具有三变量重现期u、v、r，则在区间上存在无数个连续的u、v、r组合，然而实际洪水过程具有一定历时，因此其组合个数的有限、可知的。遵循同频倍比法，当洪峰与时段洪量同频时，即可满足u=v=r条件，则洪水过程线联合重现期可通过频率组合C(u，v，r)来描述。基于此，可先运用边缘分布P-III函数推求洪峰与时段洪量的联合设计值组合，在此基础上进行同倍比方法洪水过程，从而得到多遍了联合分布模拟结果。

2 实例分析

2.1 潘家口水库库区概况

潘家口水库位于滦河上游、唐山市燕山南麓，控制径流面积8540 km2，是华北地区重要水利工程之一。库区位于燕山迎风坡降水中心地带，年平均降水量介于400 mm～700 mm；区域水系发育充分、年内分配不均，特别是7月～8月降水占全年降水的60%，为洪水多发季节。据多年暴雨资料测算显示，区域洪水过程达3 d～4 d，洪峰历时约30 h，落水在40 h～50 h之间，洪量占全年径流量的20%～40%，洪水年际差异大。监测期内(1929年～2015年)最大洪峰流量出现在1962年，洪峰流量达18800 m3/s，最大六日洪量18.53亿m3；1958年7月洪峰流量达9570 m3/s，最大六日洪量为16.52亿m3；最近的一次洪水发生在2012年，洪峰流量达4280m3/s，相应水位为226.69 m

2.2 潘家口水库设计洪水参数选定

潘家口水库兼具防洪、灌溉、饮水、养殖等多元功能，然而其设计初衷在于防患水患。其依据滦县站、栾南站的1929年～1970年间42年序列监测数据，并参考了1938年、1949年、1958年、1959年、1962年、1964年等年份的洪水资料。鉴于该项目的二期工程实施，本文将实测系列延伸至2015年；以3d、6d为基准时段，运用最大取样法计算其设计流量，并以《潘家口水库调度方式研究报告》为依据进行复核，其设计结果见表1。计算了各项参数设计值与复核值之间的绝对误差，结果表明其误差介于0.8%～3.2%之间，说明设计洪水参数稳定、可靠；另外各参数均值大部分略有偏小，只有极个别偏大，表明原设计成果相对保守、安全，基于多年来汛情特征和设计经验，故仍以最初设计值为选定标准。

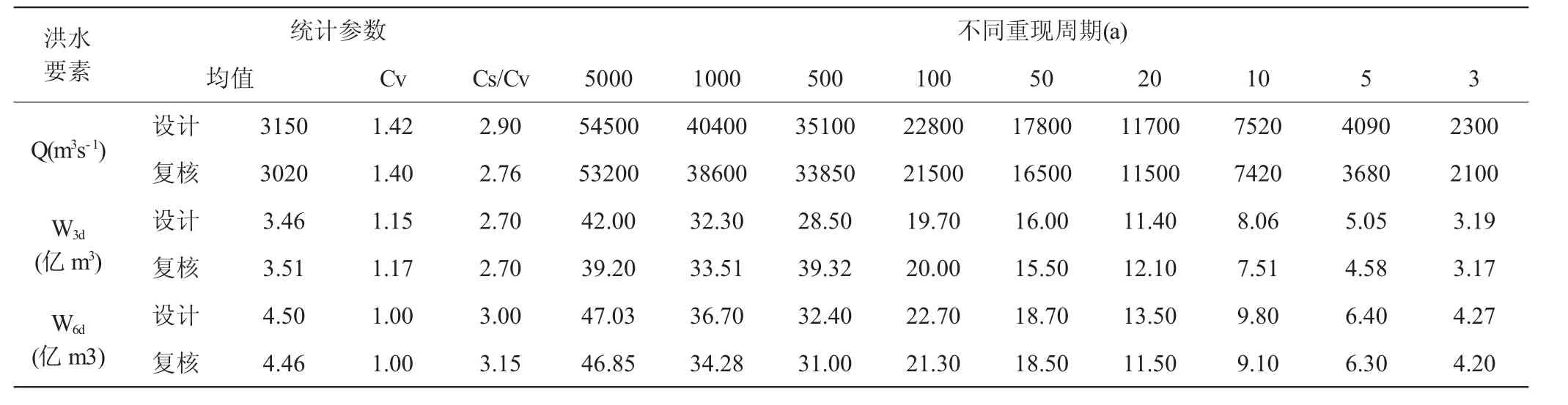
表1 潘家口水库年最大设计洪水成果

2.3 基于Copula模型的洪峰流量联合分布

洪水事件是典型的自然概率问题，最大似然估计可以精确求算一个样本集的相关概率密度，因而被广泛应用于平稳、非平稳自然变量联合分布研究中。鉴于此，参照文献[11-12]中的方案，先应用Gumbel-Hougaard Copula二维离散函数构建3 d、6 d洪量的联合分布模型，根据经验频率公式p=m(i)/(n+1)计算，并满足n个样本容量中有m(i)个联合观测样本子集服从 x≤xi且 y≤yi；得到其 kendall秩相关系数 τ分别为0.6321、0.5963；然后运用非对称 Gumbel-Hougaard Copula函数建立3 d、6 d洪量的三维联合分布模型，基于最大似然法得到参数θ分别为0.2712、0.2518；虽然潘家口水库上游建立了2个水库工程，但其为微小型水库、控制面积和库容量均较小，因而可忽略其影响。潘家口水库年最大洪峰与96 h洪量的边缘分布(P-Ⅲ)频率曲线见图1，为便于直观表达，统一采用升序排列；依图可知其边缘分布频率符合指数模型 (yW=1760.9e-0.038x，R2=0.9966；yQ= 89.116e-0.038x，R2=0.9966)，拟合良好、精度可靠。

图1 潘家口水库年最大洪峰与96 h洪量频率曲线

高超等[12]在类似于潘家口水库群的设计洪水过程线研究中分别比较了 Clayton Copula、Gumbel Copula、Frank Copula 等三种函数对洪水特征量模拟效果的差异，多站数据均显示以Frank Copula函数模拟精度最佳，基于此本文采用该函数计算潘家口水库三变量间的理论联合概率。图2-a、2-b、2-c为依次为潘家口水库的滦县站、滦南站和二站综合平均值的最大洪峰与96 h的洪量频率分布曲线。从图中可看出，各站和综合评价资料的得出的洪水特征量的理论概率点和经验概率值均密集分布于y=x直线附近，拟合函数为 (y=1.0043x+0.5142，R2=0.9966；y=1.0163x+0.3251，R2=0.998；y=1.0109x-0.9308，R2=0.9967)，均通过5%水平信度检验，说明拟合结果较好，该模拟结果合理、可信。

图2 潘家口年最大洪峰流量与168h 洪量的理论频率与经验频率拟合图

2.4 潘家口水库协防调度规则

潘家口水库目前执行的是坝前各级控制水位与限制下泄流量相结合的调度方法，即当洪水入库时，以库水位是否超过某一控制水位来判别洪水达到哪一级标准，在每一级控制水位之下则按相应的防洪标准执行某级限泄流量。潘家口水库现状洪水调度方式实施两级控泄。具体调度原则为：

①上游入库洪水达到50年一遇及以下标准洪水控泄10000 m3/s，保京山铁路大桥安全。

②50年～500年一遇洪水控泄28000 m3/s，保潘家口电站安全。

③大于500年一遇洪水不控泄。

2.5 推求设计洪水过程线

在对潘家口水库进行补测时应用阶段用暴雨移置法、水汽入流指标法及暴雨组合法，以1962年作为洪水典型年，设定联合重现周期为1000a，另补充了50a的周期；于洪峰、洪量等值区间内等距抽取200组设计值子集，经通倍比放大后按照防洪调度规律演算其汛限水位，得到其限值依次为Zmax=229.6 m、Zmin=231.5 m，这一结果于1976年以来沿用至今。基于表1中给出的潘家口洪水特征量设计值(Q=40400 m3/s，W6h=36.7亿m3)，经同频率放大推算了1955年设计洪水过程线，见图3、表2。

可知，对1995年典型洪水过程推求，以单变量同频率计算得到其最高水位为231.58 m，而双变量同频率得到其最高水位为231.69 m，这一结果表明两种设计方法对汛限调度来讲比较合理；但从防洪角度来看，单变量同频设计相当保守，不利于极端天气条件下调洪协防。

表2 潘家口水库千年一遇设计洪水调洪结果

鉴于1998年该流域发生特大洪水事件，另以该年为典型年，应用双变量同频率并推求其洪水过程线，以验证该设计的合理性，结果见表2、图4。由图4可知1998年典型年潘家口水库洪水过程历时时间长，最高洪峰流量高达21532 m3s-1，最高水位达230.304 m，洪峰历时约30 h；入库与出库流量近似同步但略有滞后。由表2可知，1962年和1988年典型年中采用双变量同频设计的潘家口洪水特征参数值略高于单变量同频设计方法，因此前者更利于库区防洪；另外以双变量的联合重现期作为防洪标准，更符合洪水过程规律，因此该方案具有科学、合理性。

图3 潘家口水库千年、五十年一遇设计洪水过程线比较(1962典型年)

图4 两变量同频率组合下潘家口水库千年一遇设计洪水调洪过程线(1998年典型)

3 结论

区别于传统单变量同频设计洪水过程线独立控制洪水各特征量重现周期，未能针对整个洪水过程联合分布进行模拟，本文利用Copula函数构造了基于长时历史洪水资料的洪水特征量多变量联合分布模型，该方案更符合防洪安全标准，适用于水文工程实际应用。

洪水过程具有随机非线性、多元化特征，Copula函数随机模拟考虑了洪水特征量直接复杂相依关系。基于双变量同频率分析，经水库调洪演算后得到洪水历时洪峰、洪量、最高水位，从而得到潘家口水库洪水过程线。相较于单变量同频模拟而言，以双变量同频推求的最高水位限值略大，并介于上下限制区间内；由此可知，基于防洪安全角度，采用双变量同频组合设计能够更好适应于气候变化背景下极端天气引起的洪水不确定性。