基于GSFLOW的片麻岩地区地表水和地下水耦合作用分析
2018-12-14何君
何 君
(山东省淮河流域水利管理局规划设计院,山东 济南 250000)
近些年来,水资源短缺已经成为全球面临的一个重要的问题,水温循环规律对于水资源的时间和空间分布具有重要的作用,随着人类气候的不断变化,地下水的过度开采,水资源的异地调用,导致不同区域的地表水和地下水相互作用越来越明显和频繁。近些年来,过度的水资源开采、水资源污染和全球变暖等气候变化对水资源和生态环境造成了极大的影响,地表水和地下水之间的相互作用也变的非常复杂,这种变化对于水资源的保护和合理利用产生了极大的影响。因此为了掌握人类活动和气候变化对水流域水循环的影响规律和机理,因此需要从过程上对地表水和地下水耦合进行分析。本文通过GSFLOW软件对地表水和地下水构建水文模型,对采集的水文数据进行地表-地下水流耦合模拟分析。
1 理论分析
1.1 地表水地下水相互作用概念模型
根据研究流域的水文条件、地址条件和地表水地下水循环特征建立地表水-地下水相互作用过程的概念模型,对水流的蒸发、径流和地表水地下水相互作用吉林进行描述。同时及时考虑流域下垫面的影响,对于下垫面的改进对水循环的过程的影响进行分析,通过考虑下垫面可以更精确的对水循环的空间分布进行模拟,得到更加精确的计算结果。地表水地下水相互作用模型如图1-A所示:

图1 -A 地表水于地下水相互作用过程图
1.2 GSFLOW计算原理
GSFLOW软件主要包括三个计算模块,第一个模块主要进行能量水流和水量的计算,采用PRMS模型进行模拟。第二个模块采用二次开发程序包对河流和湖泊进行模拟计算。第三个模块是土壤层以下区域,利用UZF等程序包进行模拟计算。GSFLOW通过将流域划分为透水区和不透水区进行水流计算,计模型如下式所示:




式中:celtop为有限差分单元格的顶板海拔;DSZ为土壤层底部重力排泄受地下水位影响的波动深度;CNDSZ为土壤区导水系数;
地下水位模拟计算公式如下所示:

式中:Kxx、Kyy、Kzz为渗透系数沿着 x、y、z轴方向的主要分量;h为水头;W为地下水的源和汇,SS为多孔介质的贮水率,t为时间步长。
2 研究区域概况
研究流域位于山东省威海市,流域面积约为1391 km2,流域内最大河流长度为65 km,该流域地势平坦,最高海拔约为896 m。该流域山区面积占总面积的17%左右。大部分丘陵山地还把在700 m左右,其中200 m~300 m的波状丘陵分布最为广泛,坡度为25度以下。土地利用/覆盖主要为耕地,约占流域面积的68.2%,居民地12.96%,林地12.5%,草地 3.42%,水域2.66%,其余为裸地。流域地形图见图1-B。

图1 -B 流域地形示意图
该流域属暖温带东亚季风区大陆性气候,四季分明,春季风大干燥,多有春旱;夏季湿热多雨,偶有伏旱;秋季温和凉爽,时有连阴雨及秋旱;冬季漫长,盛行干冷冬季风。多年平均气温11.5℃,历年极端最高气温36.4℃,极端最低气温-25.5℃。由于季风进退迟早和强弱的不同,降水的年度变化很大。年内分配不均,汛期降水量占年降水量的72%。多年平均年降雨量818 mm,最多处在昆嵛山顶达1093 mm,流域内陆面蒸发为500 mm左右。研究区降雨分布见图2。

图2 该流域降雨分布图
研究区为第四系冲洪积、冲海积、海积、湖沼积的砂、砂砾层,岩性多为细砂、中粗砂夹砾石,流域内地下水位较浅、含水层富水性较弱,地下水主要接受降水入渗补给和河水补给,多数沿地形向河谷汇集,局部受隔水层影响,在山腰或山顶出露形成山泉,但水量极小,单井出水量一般在5 m3/h~20 m3/h,极个别的单井出水量可达80 m3/h。地下水类型主要为基岩裂隙水和第四系孔隙水。基岩裂隙水主要赋存于变质岩、花岗岩和碎屑岩的风化裂隙和构造裂隙中,富水性较弱,一般埋藏较深,约为2 m~30 m,开发较为困难。基岩裂隙水的主要排泄途径:一是汇集于河谷形成河川基流;二是侧渗补给第四系或直接排泄入海;三是消耗于分散的人工开采。

图3 该流域水文地质图
3 数值模拟结果分析
(1)数值模型的建立
根据现有的地质和水文资料,对GSFLOW三维计算模型进行网格划分。共划分为110000个网格,共有76987个活动网格,为了计算方便将数值模型盖化为两层,其中第一层为含水层,第二层为承压含水层。数值模型如图4所示。采用模型计算初始时段的浅层地下水水位,通过水位计算方法,获得含水层的初始水位,通过模拟计算,对上下两层的初始渗流场进行模拟。含水层渗透系数的确定主要参考研究区渗透系数空间变异性分析成果,孔隙度及给水度、降雨入渗系数等水文地质参数主要根据水文地质资料确定。

图4 数值计算模型
(2)GSFLOW模拟结果

图5 某流域流量模拟结果与实测值对比图
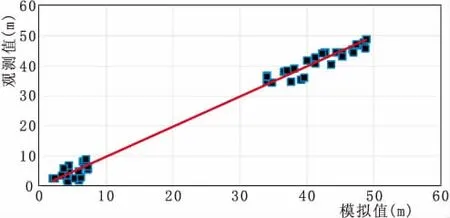
图6 地下水位对比图
将流域内的月径流量模拟结果与检测结果进行对比分析如图5所示,从整体数据变化趋势来看,数值模拟计算结果与检测结果具有较好的对应性。在概率期,确定性系数为0,85,在模型期,确定性系为0.76,在这两个时期模型的确定性系数均大于0.7,并且概率期确定性系数比模型期概率系数大11.8%,对于大流域流量模拟来说,采用GSFLOW模型模拟结果较好,精度较高。如图6所示为,在模拟期间地下水位拟合结果图,如图所示拟合结果所示,检测水位的计算值与观测值的误差为0.3 m,相关系数为0.925,符合模拟要求。
(3)地下水开采对地表水和地下水相互作用的分析
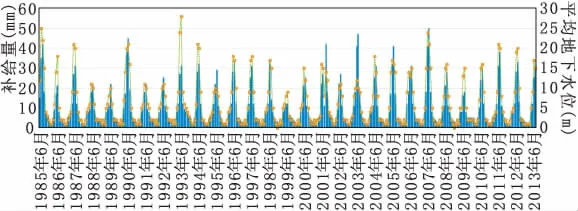
图7 现状开采下地下水位模拟结果

图8 减少50%开采下地下水位模拟结果
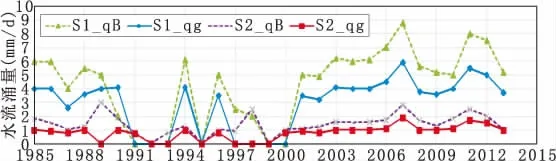
图9 不同开采方案向下地下水侧向补给量与河道基流量模拟结果
通过图7~8可知,随着地下水开采的减少,地下水位动态特征呈现升高趋势,在现状地下水开采情况下,随着地下水开采量的减少,河道基流量为由0逐渐变恢复河道基流量,同时地下水侧向补给量也一定程度上增加,通过模拟分析可知,在地下水开采过程中,随地下水位的增加河道基流量呈现增加趋势。
4 结论
(1)通过对流域内水流进行模拟分析可知,在概率期,确定性系数为0.85,在模型期,确定性系为0.76,在这两个时期模型的确定性系数均大于0.7,并且概率期确定性系数比模型期概率系数大11.8%,检测水位的计算值与观测值的误差为0.3 m,相关系数为0.925,符合模拟要求。
(2)随着地下水开采的减少,地下水位动态特征呈现升高趋势,随着地下水开采量的减少,河道基流量为由0逐渐变恢复河道基流量,同时地下水侧向补给量也一定程度上增加在地下水开采过程中,随地下水位的增加河道基流量呈现增加趋势。
