基于模型过滤的多任务回归在帕金森症预测中的应用

刘 峰，季 薇，李 云

(1.南京邮电大学 通信与信息工程学院，南京 210003； 2.南京邮电大学 计算机学院，南京 210023)(*通信作者电子邮箱873216019@qq.com)

0 引言

帕金森症(Parkinson’s Disease，PD)是继阿尔茨海默氏病后第二大常见的神经退行性疾病，仅中国大陆就有超过300万人受到该病的影响[1-2]。它的主要症状是肌肉僵硬、运动过缓、静止性震颤以及其他一些运动障碍[3-4]。临床实践中，医生大多采用统一帕金森定量表(Unified Parkinson’s Disease Rating Scale, UPDRS)[5-6]来衡量患者帕金森症症状的严重性。已有研究表明，60%～90%的帕金森患者会出现语言障碍，患有某种程度上的语音损伤，语音损伤也可能是帕金森最早的征兆之一[7], 因此，可以通过语音分析来对患者的病情进行早期诊断。

近几年研究中，Goetz等[8]强调了利用语音信号预测UPDRS 的重要性；Tsanas[9]在此基础上使用了各种语音信号处理算法得到了相关病特征，并利用传统的机器学习方法(如最小二乘(Least Squares, LS)、决策回归树等)预测帕金森症患者的 motor-UPDRS(motor Unified Parkinson’s Disease Rating Scale) 评分和 total-UPDRS(total Unified Parkinson’s Disease Rating Scale)评分；文献[10-11]在此基础上介绍了基于参数优化的支持向量机的帕金森病诊断方法，证明了经参数优化的支持向量机可以提高帕金森病诊断的准确率；Athansios等[12]则通过语音测试来证明UPDRS评估具有临床上有用的准确性，同时指出motor-UPDRS和total-UPDRS受不同语音特征影响，其在预测motor-UPDRS和total-UPDRS时，贡献度并不相同。然而，Tsanas只考虑了在单任务条件下利用各种语音特征预测motor-UPDRS 和total-UPDRS分析病情，但是并没考虑到在多任务学习过程时，子任务语音特征对motor-UPDRS和total-UPDRS的贡献度的不同，各子任务的共享特征也会影响到其他子任务的预测效果。较之于单独的学习各个子任务，对于多个相关的子任务同时学习能有效地提升预测性能[13], 并且，一致性原理[14]又对此给出了理论保障，即若最大化各相关子学习机的一致性，则能使各子学习机的性能得到改善。Evgeniou等[15]提出了正则化多任务学习(regularized multi-task learning)方法，其思想是在保持各个自学机局部优化的同时，使得多个学习机之间的全局差异最小化。正则化多任务学习以其模型的简洁性从而成为多任务学习理论研究基础。

本文考虑到了在预测motor-UDPRS和total-UPDRS时，子任务语音特征之间相互影响，通过特征选择，合理利用子任务之间的共享特征，使得模型可解释性更强，模型更为稀疏。同时在考虑不同对象分布域不同的基础上，添加了过滤机制，提出了基于模型过滤的多任务回归算法来解决帕金森UPDRS多任务预测问题。

1 帕金森语音预处理

1.1 语音数据集描述

本文采用UCI远程帕金森数据集，数据集详见文献[8]。数据集包含了42位原发性帕金森患者的采集信息，其中男性共有28位，女性占了14位，每一位患者都有5年的患病历史。采集数据期间，病人每周完成医生制定的一系列测试，并记录该病人的6条语音，持续6个月，由此一共采集了5 875条语音音频，其中男性占4 010条，女性占1 865条。

1.2 语音特征提取及选择

1.2.1 帕金森语音特征提取

利用录制到的语音音频对帕金森症患者UPDRS进行预测时，首先需要经过去噪算法以及各种语音信号处理算法处理得到相关语音特征, 例如谐波噪声比(Harmonic to Noise Ratio，HNR)、噪声谐波比(Noise to Harmonic Ratio，NHR)、趋势波动分析(Detrended Fluctuation Analysis，DFA)、循环周期密度熵(Recurrence Period Density Entropy, RPDE)和基因周期熵(Pitch Period Entroy, PPE)等; 然后，将帕金森病理特征向量作为输入向量，通过构建的模型，得到患者UPDRS。本文采用文献[5,8,11]中介绍的语音信号处理算法进行帕金森语音处理，详见表1。

表1 语音信号处理方法

通过上述线性和非线性语音信号处理方法，能够将1条语音处理成一个16维的语音特征向量，每一维表示一个提取的语音信号特征值。经过语音特征的提取，得到一个5 875*16的数据集。

1.2.2 帕金森语音特征选择

基于L1正则化的学习方法则是一种嵌入式特征选择方法，其特征选择过程和学习器训练过程融为一体，同时完成[16]。本文在构建模型时引入L1正则化项，进行帕金森语音特征选择，从而合理利用子任务之间共享的帕金森语音特征，使得各子任务差异性更小，提高预测模型的稀疏性和泛化能力。

2 基于模型过滤的多任务回归算法

2.1 数据集分析

在数据集预处理阶段，本文随机选取了5个对象，画出motor-UPDRS随时间变化的曲线，如图1所示。本文发现，不同对象之间的帕金森病情进展有显著的不同。其中，如对象1和对象2，两者之间变化规律的差异性很大；相反，对象1和对象5曲线变化规律却非常相似。很显然在进行对象1的UPDRS预测时，本文须考虑帕金森对象分布在不同的域对预测模型的影响，否则模型的精确度将会大幅降低。因此本文添加过滤机制，来区分不同帕金森对象，提高预测精确度。

图1 对象motor-UPDRS值随时间变化规律

2.2 多任务回归模型过滤

在本实验中UPDRS的预测作为一个多任务回归问题，结合帕金森对象病情之间的差异性这一事实，提出了基于模型过滤的多任务回归方法(Multi-Task Regression Model Filtering， MTRMF)。该模型算法包含三部分：多任务回归算法构建模型并进行特征选择、添加过滤机制进行模型融合。多任务回归构建模型部分，则将N-1个已知对象数据构建N-1个多任务回归模型；添加过滤机制部分，则利用验证集数据对N-1个回归模型进行过滤，具体步骤详见实验；模型融合部分，则将过滤之后的剩余模型进行融合，获取待测对象的最终预测模型，从而提高算法的泛化能力。

设训练数据集中包含N个对象,共n条语音记录，X∈Rn×d为输入语音特征矩阵；Y∈Rn×t为UPDRS值矩阵，即帕金森病人motor-UPDRS值和total-UPDRS值；W∈Rd×t为模型参数矩阵。其中:d为帕金森语音特征向量维度，n为语音数据记录数，t为任务数。λ1为L1正则化参数，λ2为L2正则化参数。

建立模型如下：

(1)

在求解模型之前引入如下定理：

定理1 假设F1和F2是两个下半连续的凸函数，F2在Rn×m中可微且对某个β∈(0,+∞)满足β-Lipschitz连续，即为:

‖▽F2(U)-▽F1(V)‖F≤β‖U-V‖F

(2)

则对于凸优化问题：

(3)

有如下性质：

1)如果F1+F2是强制的，即为：

(4)

则问题2)至少有一个解。

2)如果F1+F2是严格凸的，则问题2)至多存在一个解。

3)如果F1和F2同时满足条件1)和条件2)，则问题2)存在唯一解，且对任意的初始值X0及0<δ<2/β，用如下方法生成的迭代序列Xk+1收敛到问题2)的唯一解：

Xk+1=proxδF1(Xk-δ▽F2(Xk))=

(5)

其中，k为迭代次数，且性质(3)所描述的求解算法通常称之为近邻前向后向分裂(Proximal Forward Backward Splitting，PFBS)算法。证明详见文献[17]。

定理2 对任意的τ>0,Y∈Rn×m，矩阵收缩算子ζτ(Y)满足

sign(Y)·max(0,|Y|-τ)

(6)

其中sign(·)为符号函数。证明详见文献[18]。则MTRMF模型问题求解转化为:

Wk+1=

(7)

MTRMF算法伪代码如下：

算法 基于模型过滤的多任务回归算法(MTRMF)。

输入Xn×d,Yn×t,λ1,λ2,δ;

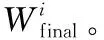
fori=1,2,…，N

1) 进行预处理Xn×d

2) 设定迭代次数k，和正则化参数λ1，λ2

3) forj=1,2,…,N-1

form=1,2,…,k

end

end

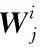
5) 添加过滤机制，获得剩余符合条件的M个模型

end

3 实验与分析

将数据集中任一对象作为待预测对象，其他N-1对象作为已知对象建立模型进行对比实验；同时将待测对象的数据平均分为3部分，前1/3作为验证集，使用N-1个训练出的回归模型对其进行预测，并计算出平均绝对误差(Mean Absolute Error, MAE)值来衡量N-1个模型对待测对象的表现性能。其中，将MAE值大于阈值σ的模型进行过滤，并选出剩余较好的M个模型进行融合。后2/3作为测试集进行模型预测，同样使用MAE来衡量融合后模型的性能。

实验分别比较了单任务条件下最小二乘(Least Squares, LS)法[6]、加权迭代的最小二乘法(Iteratively Reweighted Least Squares, IRLS)[9]、决策回归树(Classification and Regression Tree, CART_rg)[4]以及多任务回归模型(MTRMF)的预测效果。在实验训练阶段，IRLS设置迭代次数为100，迭代次数采用文献[9]设置的迭代次数。MTRMF模型迭代次数设置为100，delta设置为0.000 01，lmada2设置为0.2。根据文献[11]得出的结论，帕金森选择的特征数达到13时, F-Measure趋于稳定，并且错误率达到最低。由此可以得出当帕金森病理特征选择数目达到13时，模型的泛化能力，可解释性达到最佳。经过实验，本文设置lmada1为12.5，预测效果达到最佳； 同时，在进行模型过滤时，阈值σ设置为8。最终motor-UPDRS对比实验结果如图2所示，total-UPDRS对比实验结果如图3所示。

由图3可知，在大部分对象预测的表现上，MTRMF比单任务条件下LS，IRLS和CART_rg预测的误差更小。为了精确描述MTRMF性能，本文采用MAE的方差来衡量算法稳定性。实验结果如表2所示。

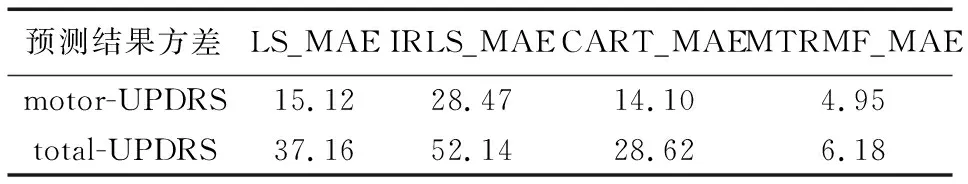
表2 各回归算法预测MAE结果的方差

由表2可知，基于模型过滤的多任务回归模型在预测UPDRS时,比单任务条件下LS模型预测motor值准确度提高了67.2%；预测total值则提高了83.3%。相比单任务条件下CART_rg预测motor值提高了64%；预测total值则提高了78.4%。同时在实验时利用L1正则化项进行特征选择发现，模型对于振幅扰动类特征、HNR、RPDE和DFA等特征更为偏好，预测效果相较于单任务回归算法得到极大提升。为了验证挑选出的13种特征是否有效，本文将挑选出的特征在单任务下用最小二乘法(LS)进行训练，发现当剔除Jitter(Abs)、Jitter(RAP)、Jitter(PPQ5)这三种特征后，最小二乘法(LS)预测模型效果基本不变，如表3所示。结果表明，本文方法在进行特征选择时，并没有漏除重要语音特征，相反回归模型变得更为稀疏，预测性能更好。实验表明在多任务回归模型中添加L1正则化项进行特征选择有助于模型稀疏化，也提高了模型的泛化能力和模型的可解释性。进一步表明，在预测病人UPDRS时，一定要注意采集语音期间病人连续稳定发声，实验时应该多关注HNR、RPDF、Shimmer类特征的变化。

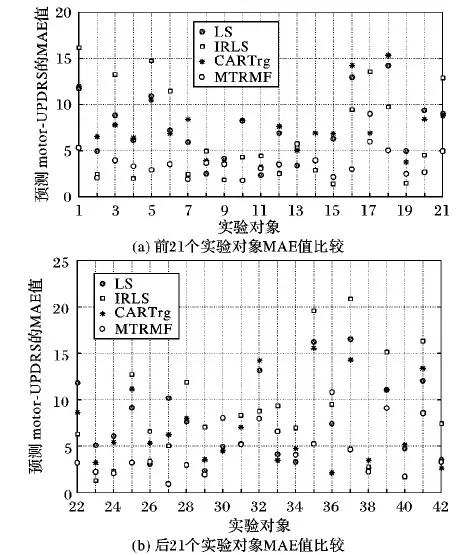
图2 在帕金森数据集各对象上预测motor-UPDRS的MAE比较

预测结果方差特征选择前LS_MAE特征选择后LS_MAEmotor-UPDRS15.1214.52total-UPDRS37.1635.16

4 结语

本文将多任务回归模型应用到远程帕金森数据集中，实现了对motor-UPDRS和total-UPDRS的联合预测, 并且与单任务条件下最小二乘法、决策树回归等传统回归方法比较。实验表明，在帕金森UPDRS预测过程中，对于多变量预测、多任务回归模型比单任务模型更加有效。该方法在建模过程中利用L1正则化项进行特征选择，使得模型更为稀疏，模型可解释性更强，模型的泛化能力与传统单任务模型相比，得到了极大的提升。同时本模型考虑到了帕金森对象的差异性，使用已有的验证数据在模型融合前进行过滤，使得预测效果变得更好的前提下，模型的稳定性得到增强。当然，本文只考虑了不同对象分布在不同的域中，但是如何取测量不同时间维度下的帕金森UPRDS数据的发展以及病情程度的相似度问题，将是下一步工作的重点。

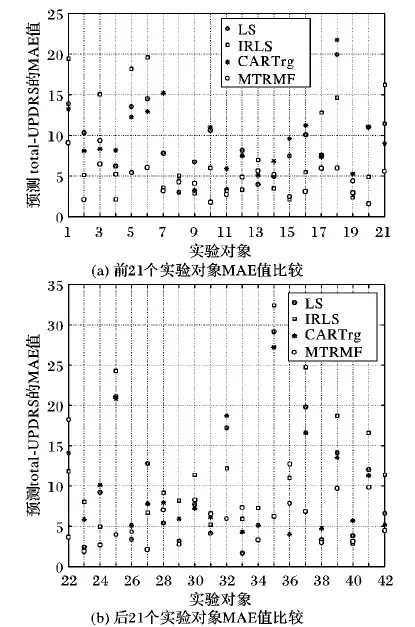
图3 在帕金森数据集各对象上预测total-UPDRS的MAE比较