基于因子图算法的INS/GPS信息滞后处理方法
2018-12-14高军强汤霞清郭理彬
高军强,汤霞清,张 环,郭理彬
(陆军装甲兵学院 兵器与控制系,北京 100072)(*通信作者电子邮箱gjqxkl8990@163.com)
0 引言
惯性导航系统/全球定位系统(Inertial Navigation System/Global Positioning System, INS/GPS)组合导航系统能够充分发挥INS和GPS各自的优点,被认为是目前最理想的组合方式,广泛应用于精确制导武器、测绘、航空航天等领域[1-2]。然而,由于INS/GPS组合导航系统中的GPS信息一般滞后于INS信息,为了对同一量测时刻的INS、GPS信息进行融合就需要组合导航系统信息融合时刻也必须滞后于量测时刻,从而对系统实时性造成了不良影响[3-4]。
目前,消除信息滞后对INS/GPS性能影响的主要方法可以分为两种: 一种方法是进行时间配准,即将不同信息源的量测信息统一到同一时刻,使组合导航系统信息融合时刻处理的是不同信息源在同一时刻的量测信息,代表方法有曲线拟合法、拉格朗日插值法、最小二乘虚拟法、内插外推法等,然而经时间配准方法处理后的量测信息实际上都引入了新的误差,在工程应用中也存在一定的局限性和片面性[5-6]; 另一种方法是直接在滤波算法中融合各信息源在不同时刻的量测信息,如将信息滞后时间扩充为系统状态进行估计的增广状态法[7]、基于新息重组理论建立最优滤波器的方法[8]、考虑量测信息滞后的非等间隔滤波算法[9]等。针对采用卡尔曼滤波的INS/GPS组合导航系统,将基于INS机械编排的时间更新过程与利用GPS信息进行修正的量测更新过程分解为两个独立的任务,在接收到GPS信息之前只进行时间更新过程,待接收到GPS信息之后再进行量测更新过程,能够避免由于GPS信息滞后带来的等待问题,保证系统的实时性,但需要对卡尔曼滤波进行较大的调整,系统精度也受到了一定影响[10-11]。
因子图算法将组合导航信息融合问题描述为在因子图模型中连接因子节点,通过因子图模型推理实现组合导航结果的求解。因子图模型良好的扩展性和灵活性,使其可以高效、快速地融合异步量测信息,在多传感器组合导航系统中逐渐受到越来越多的关注[12-13]。本文将因子图算法应用于INS/GPS组合导航系统,研究了INS/GPS因子图模型的构建及推理方法,提出了在因子图模型中处理信息滞后的方法与INS误差修正方案,并进行了仿真实验与分析。
1 基于因子图的INS/GPS信息融合算法
1.1 INS/GPS组合导航数学模型
INS/GPS组合导航系统中的状态变量一般是由位置、速度、姿态、惯性传感器偏差构成的15维向量[14]。由于惯性传感器偏差是用于对INS中惯性测量单元(Inertial Measurement Unit, IMU)的测量误差进行修正,并不需要进行导航输出。因此,将状态变量分为导航状态量x和惯性传感器偏差状态量α两个部分,分别为:
(1)
(2)
式中:λ、L、h分别表示经度、纬度、高度;vE、vN、vU分别表示东向、北向、天向速度;θ、γ、ψ表示姿态角;εx、εy、εz表示陀螺仪偏差量;▽x、▽y、▽z表示加速度计偏差量。
组合导航系统输出周期为T=ti+1-ti(i=0,1,2,…),在ti时刻输出的导航状态量为xi,惯性传感器偏差状态量为αi,则截止到tk时刻组合导航系统输出序列和惯性传感器偏差状态量序列可以分别表示为集合的形式:
Xk={x0,x1,…,xk-1,xk}
(3)
Αk={α0,α1,…,αk-1,αk}
(4)
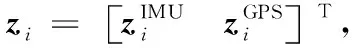
Zk={z0,z1,…,zk-1,zk}
(5)
INS/GPS组合导航信息融合的任务便可以表示为求解联合概率分布p(Xk|Zk)的最大后验概率估计问题:
(6)
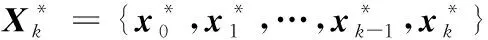
因子图算法采用因子图模型描述式(6)所示最大后验概率估计问题,然后通过对因子图模型进行推理,求出最大后验估计值, 其算法核心包括因子图模型构建与因子图模型推理两部分。
1.2 INS/GPS因子图模型构建
因子图模型是一种二分图模型,由变量节点、因子节点以及表示变量节点与因子节点间依赖关系的边构成,记tk时刻的INS/GPS因子图模型为:
Gk=(Fk,Ωk,Ξk)
(7)

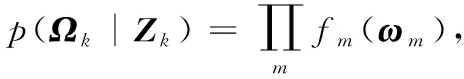
(8)
由式(3)~(5),Xk、Αk、Zk中的变量随时间的推移越来越多,故因子图模型中的变量节点、因子节点、边也在不断增多。下面以时刻由tk-1推移到tk,Gk相对于Gk-1的变化,说明INS/GPS因子图模型的具体构建方法。
由tk-1到tk,状态变量中增加了xk和αk,故在因子图中添加两个变量节点,分别为Ωxk=xk,Ωαk=αk,为便于表示,在因子图中Ωxk直接记作xk,Ωαk直接记作αk。
一般情况下,惯性传感器偏差随时间的传播可以用一个非线性函数描述,这意味着可以由当前时刻的偏差预测下一时刻的偏差。将αk-1对αk的预测结果g(αk-1)看作是对αk的量测信息,则得到偏差因子节点的表达式为:
(9)
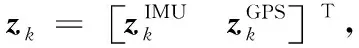
(10)
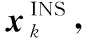
(11)
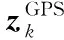
(12)

1.3 INS/GPS因子图模型推理方法
因子图模型的推理就是利用联合概率分布,在已知图结构和证据的情况下,回答查询问题。对于组合导航系统因子图模型需要解决的最大后验概率查询问题,目前主要有最大化-乘积消元算法、最大化-乘积团树算法等[18]; 然而,传统推理方法一般用于事后处理,在一次推理中默认对模型中的所有状态变量进行求解,这对于随时间增长而不断增添状态变量的组合导航系统因子图模型而言,求解效率势必会不断下降,显然无法满足导航系统实时性要求。
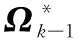
图1 tk时刻INS/GPS因子图模型
本文INS/GPS因子图模型推理方法以iSAM2算法为核心,并结合INS/GPS系统特点进行了两方面的调整:一是将惯性导航解算结果作为迭代估计中变量的初值,由于INS具有很高的短时精度,采用组合导航结果能够对INS误差积累进行有效修正,保证了每个时刻的惯性导航解算结果与最优估计值相差较小,将其作为初值可以减少高斯牛顿迭代的次数,从而提高最优估计值的求解速度;二是iSAM2算法中为了对历史状态量进行平滑得到更高的估计精度,设计了流动重新线性化过程,而考虑到导航系统更重要的是关注当前时刻状态量的估计,对历史时刻状态量的平滑没有太大意义,故在推理时不进行重新线性化,从而进一步提高了因子图模型推理效率。
从添加新的节点到完成一次最优估计的步骤如下:
步骤1 增添新的变量节点和因子节点;
步骤2 利用惯性导航解算结果设置新增添状态变量的初值;
步骤3 对新增添的因子节点进行线性化处理;
步骤4 查找原因子图中受新增添因子节点影响的部分;
步骤5 用高斯牛顿迭代方法计算需要求解的状态变量的更新量;
步骤6 初值+更新量,得到最优估计值。
2 因子图算法中信息滞后处理方法
进一步研究图1所示INS/GPS因子图模型,如果系统由INS/GPS变为单一INS,那么只需要将GPS因子节点去掉便可得到INS因子图模型,这正是因子图模型良好灵活性和扩展性的体现。文献[10-11]采用的GPS信息滞后处理方法,在因子图算法中的实现非常简便。
2.1 GPS信息滞后时的因子图模型及讨论
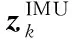
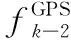
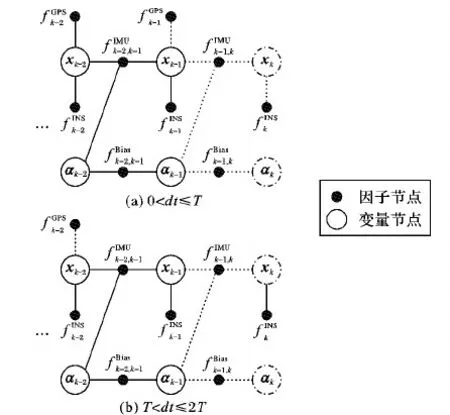
图2 存在GPS信息滞后时tk时刻INS/GPS因子图模型
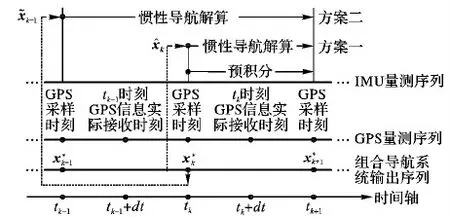
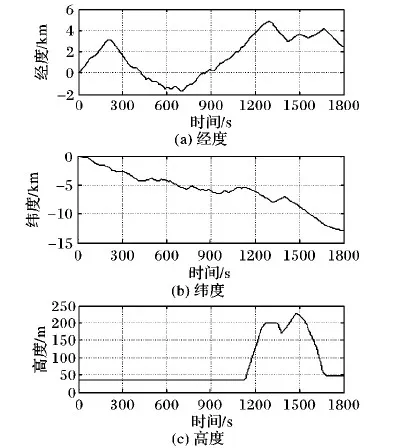
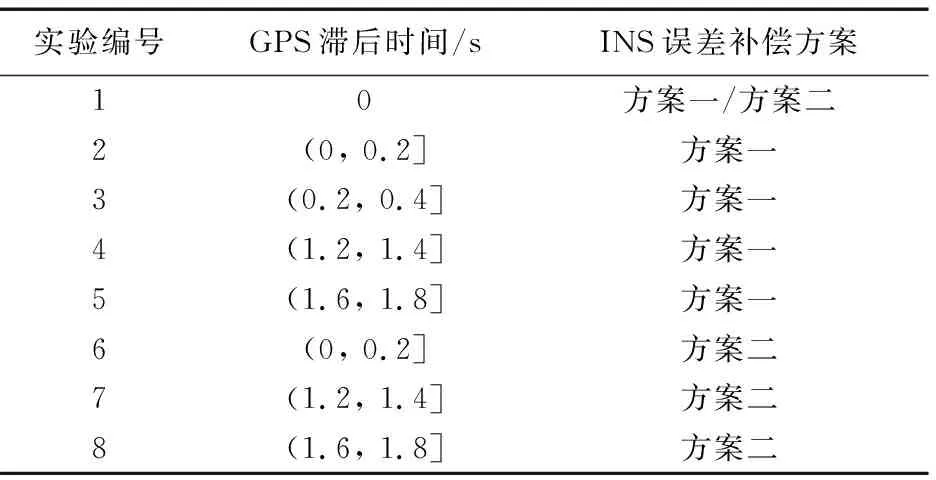
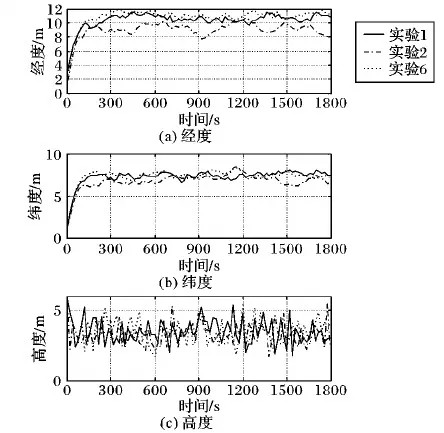
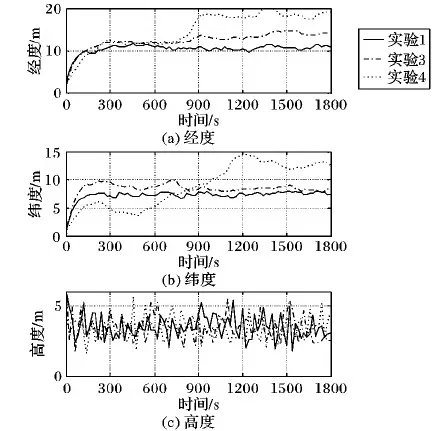
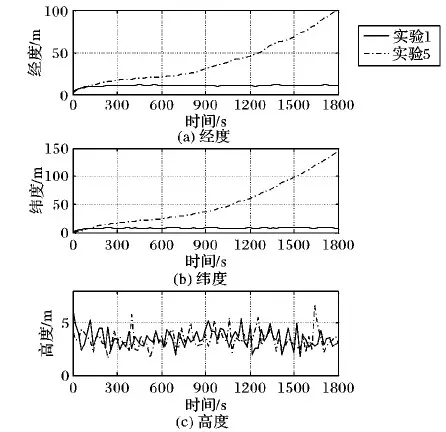
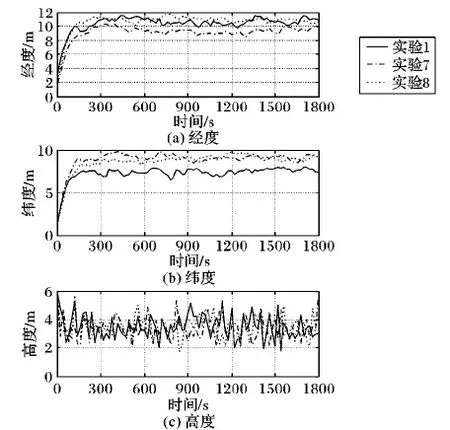
前文指出,图1、图2(a)、图2(b)均是tk时刻的INS/GPS因子图模型,3个模型之间存在差异的原因在于GPS信息滞后时间不同。现在换一个角度考虑,将图1、图2(a)也视作当T (13) (14) (15) 总结以上对比,从精度的角度,图1优于图2(a)优于图2(b);从实时性的角度,图2(b)优于图2(a)优于图1。组合导航系统设计在精度与实时性之间的权衡是亘古不变的命题,本文研究的出发点是在保证最高实时性的前提下,实现相对更高的精度。 INS误差修正是指将组合导航结果作为惯性导航解算的初始值,从而消除INS中的误差积累,这是保证组合导航系统精度的关键。当不存在信息滞后时,毋庸置疑地采用上一时刻的实时导航状态量作为惯性导航解算的初始值,对上一时刻到当前时刻之间的IMU量测数据进行解算,能够有效消除INS中的误差积累; 然而,当存在信息滞后时,为了保证系统实时性,需要在接收到GPS量测信息前将精度较低的预测结果作为实时导航状态量进行输出,而较早时刻的导航状态量已经是量测更新结果,精度较高。因此,在对INS误差进行修正时便存在两种方案可供选择。 方案一 采用上一时刻的实时导航状态量进行INS误差修正,不考虑其是否进行了量测更新。该方案的优点在于,每次只对一个系统输出周期内的IMU量测数据进行解算,从而保证了误差积累最小,并且无需储存历史IMU量测数据。缺点在于,如果上一时刻的实时导航状态量是预测结果,将有可能无法有效修正INS误差。 方案二 采用上一时刻因子图模型推理结果中刚刚完成量测更新的导航状态量进行INS误差修正,对该导航状态量对应时刻到当前时刻之间的IMU量测数据进行解算。该方案的优点在于,采用量测更新结果能够保证有效修正INS误差;缺点在于,需要储存一段时间的IMU量测数据,并且一次INS解算的时间段越长,就会在解算过程中产生越大的误差积累。 为了直观对比两种INS误差修正方案,图3给出了存在GPS信息滞后时因子图算法的处理时序,并对两种INS误差修正方案进行了标记。 设置INS/GPS组合导航系统输出频率为5 Hz;INS测量频率为100 Hz,陀螺常值漂移为0.02 °/h、随机漂移为0.01 °/h,加速度计的常值零偏为100 μg,随机零偏为50 μg;GPS测量频率为1 Hz,经度、纬度测量噪声均方差为10 m,高度测量噪声均方差为15 m,3个方向速度测量噪声均方差都为0.1 m/s;总仿真时长1 800 s,设计仿真轨迹如图4所示。 图3 GPS信息滞后时因子图算法处理时序及INS误差修正方案 图4 运动轨迹仿真 为了分析存在信息滞后时因子图组合导航算法的性能,比较两种INS误差修正方案在不同GPS信息滞后时间下的处理效果, 进行8组仿真实验。每组仿真实验中分别进行50次蒙特卡罗仿真,采用均方根误差(Root Mean Square Error, RMSE)评价组合导航精度。各组仿真实验中,GPS信息滞后时间及INS误差修正方案设置如表1所示。其中,实验1为不存在信息滞后的理想状况,作为误差参照基准。由于不存在信息滞后时,上一时刻实时导航状态量便是刚刚完成量测更新的导航状态量,故两种INS误差修正方案是等价的。 表1 仿真实验参数 图5所示为实验1、2、6位置RMSE曲线对比,当GPS信息滞后时间为(0, 0.2]时,采用方案一和方案二均得到了与不存在GPS信息滞后时相当的组合导航精度,说明因子图算法凭借其可以在一个信息融合时刻处理各信息源不同时刻量测信息的特点,非常成功地处理了信息滞后带来的影响。 图5 实验1、2、6位置RMSE曲线对比 图6所示为实验1、3、4位置RMSE曲线对比,采用方案一进行INS误差修正时,随着GPS信息滞后时间的变长,高度误差几乎不受影响,而经度误差和纬度误差出现了明显增大,组合导航结果精度越来越差。这是由于GPS信息滞后时间越长,组合导航结果就是时间跨度越长的预测结果,其精度受INS误差积累的影响越大,对INS误差修正作用也就越小。 图6 实验1、3、4位置RMSE曲线对比 图7为实验1、5位置RMSE曲线对比,当GPS信息滞后时间达到(1.6, 1.8]时,经度误差和纬度误差随时间发散,当载体高度方向发生位移时,高度误差也明显增大,此时方案一已经无法有效修正INS误差。以上分析表明:方案一只能在较小的GPS信息滞后情况下,对INS误差起到有限的修正作用,当GPS信息滞后时间变长,该方案的导航误差会越来越大,甚至发散,不具备长航时导航的能力。 图7 实验1、5位置RMSE曲线对比 图8所示实验1、7、8位置RMSE曲线对比,采用方案二进行INS误差修正时,即便GPS信息滞后时间达到(1.6, 1.8]也能得到与不存在GPS信息滞后时相当的导航精度。说明,INS误差积累会在每一次修正中得到有效消除,保证了组合导航精度的长期稳定。 图8 实验1、7、8位置RMSE曲线对比 以上分析表明,当GPS信息滞后时间不超过组合导航系统输出周期时,直接采用实时导航状态量对INS误差进行修正,计算量小且不需要额外的存储空间便可以实现与没有滞后时非常接近的导航精度;但是当GPS信息滞后时间超过组合导航系统输出周期时,采用实时导航状态量对INS误差修正效果变差,甚至有可能导致误差发散。这种情况下,如果采用上一时刻因子图模型推理结果中刚刚完成量测更新的导航状态量对INS误差进行修正,则可以取得更好的效果。基于INS/GPS因子图组合导航算法的GPS信息滞后处理方法很好地解决了信息滞后带来的不良影响,对存在信息滞后的组合导航系统设计具有一定参考意义。 采用因子图算法实现INS/GPS组合导航系统信息融合,避免了系统实时性因GPS信息滞后而变差,同时又能保证很高的系统精度。因子图算法利用接收到的量测信息建立因子节点,将其连接到因子图模型中对应的变量节点上进行因子图模型推理便可求得信息融合结果。因子图算法可以在一个信息融合时刻处理不同时刻的量测信息,使其对于受异步、滞后等因素影响的多传感器信息融合问题有很强的适应性。因子图算法对子系统进行反馈校正时,由于不同时刻可用的量测信息不同,导致因子图模型推理结果中不同时刻状态量的估计精度差别较大,因此需要尽量采用估计精度较高的状态量进行反馈,以改善组合导航系统的精度。本文采用完成量测更新的导航状态量对INS误差进行修正时需要储存一段时间的IMU量测数据,当GPS信息滞后时间太长时,求解效率有所下降,故因子图模型实时推理方法以及在多传感器信息融合中的应用有待进一步研究。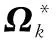
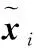
2.2 INS误差修正方案
3 仿真实验与分析
4 结语
