改进的飞蛾扑火优化算法在网络入侵检测系统中的应用

2018-12-14叶志伟

计算机应用 2018年11期

徐慧，方策，刘翔，叶志伟

(湖北工业大学计算机学院，武汉430068)(*通信作者电子邮箱xuhui@mail.hbut.edu.cn)

0 引言

网络入侵检测系统(Network Intrusion Detection System, NIDS)[1]能及时检测网络入侵事件，减小网络入侵的破坏。NIDS主要以系统日志的方式作为数据源，判断待检测数据是否属于正常数据，但是并不是每一项数据都可以帮助我们筛选攻击数据，所以对数据进行特征选择[2]是提升NIDS的可靠性和时效性的有效方法之一。对数据特征选择就是保留数据中贡献度较大特征，去掉一些冗余特征甚至噪声特征，目前特征选择的主要算法有二进制粒子群优化(Binary Particle Swarm Optimization, BPSO)算法[3]、遗传算法[4]、二进制灰狼优化(Binary Grey Wolf Optimization, BGWO)算法[5]、二进制布谷鸟搜索(Binary Cuckoo Search, BCS)算法[6]等; 但它们或多或少都存在一些问题，例如遗传算法随机性比较大，BGWO算法易陷入局部最优等。

飞蛾扑火优化(Moth-Flame Optimization, MFO)算法[7-8]是2015年由Mirjalili等提出的一种智能优化算法，它源于飞蛾围绕火焰飞行的行为模拟, MFO已被证明在电力[9]、工程[10]、网络[11]和加工制造[12]等方面具有很好的效果。MFO算法中飞蛾只根据自己的火焰更新位置，所以局部搜索能力很强，但全局收敛性较差，而且易陷入局部最优。为此，文献[13]中结合了Lévy飞行搜索策略提出了一种LMFO(Moth-Flame Optimization algorithm based on Lévy flights)算法，Lévy飞行搜索策略具有小步移动多、偶尔大步移动的特点，扩大了MFO的搜索范围; 文献[14]中提出一种纵横交叉混沌捕焰优化算法，采用纵横交叉机制，将火焰之间和火焰的不同维度之间相互结合，并引入混沌算子，提高了算法精确度和跳出局部最优能力。

尽管MFO算法应用和改进比较广泛，但还没有应用于网络入侵检测中, 因此，本文尝试将MFO结合粒子群优化(Particle Swarm Optimization，PSO)算法以提升MFO的全局搜索能力和收敛速度。

1 相关算法

1.1 飞蛾扑火优化算法

对MFO中M表示飞蛾的集合，OM表示飞蛾M所对应的自适度的值,F为火焰的集合，OF表示火焰F对应的自适度的值。飞蛾F和火焰M都是函数的解，飞蛾和火焰的不同之处在于它们的更新方式不同，火焰是飞蛾目前为止的历史最优解。飞蛾扑火算法的近似优化如下：

飞蛾的集合为M，其中Mi为第i个飞蛾，Mij为第i个飞蛾对应位置：

火焰的集合为F，其中Fi为第i个火焰，Fij为第i个火焰对应位置：

MFO优化算法是近似于求全局最佳的三元组：

MFO=(I,P,T)

(1)

I是一种产生随机飞蛾种群和其对应的适应度值的函数，其系统模型如下：

I:φ→{M,OM}

(2)

P是搜索飞蛾周围空间的主函数，P函数接受矩阵M并返回其更新的最终值：

P:M→M

(3)

T是飞蛾更新的截至条件，若T不满足，则程序会一直运行

T:M→{true,false}

(4)

使用I、P和T描述MFO算法的框架一般定义如下：

M=I()

whileT(M) is equal to false

M=P(M);

End

I()函数初始化飞蛾种群M，用P函数移动搜索飞蛾M周围空间，迭代更新飞蛾M直至迭代停止条件T(M)满足。该算法的启发是飞蛾的横向飞行，为了建立这种数学模型，飞蛾借助火焰的更新的函数如下：

Mi=S(Mi,Fj)

(5)

每个飞蛾相对于火焰的位置的更新函数如下：

S(Mi,Fj)=Diebt·cos(2πt)+Fj

(6)

其中:Di表示飞蛾到火焰的距离，b是一个常量定义螺旋线的形状，t是一个属于[-1,1]内的随机数，Di的计算公式如下：

Di=|Fj-Mi|

(7)

由于飞蛾的更新公式为式(6)，已知函数为y=et·cos(2πt)时，当t属于[-1,1]内的随机数时，离飞蛾位置越近的点更新到的可能性越大，这样容易使得飞蛾易陷入局部最优。为了使飞蛾尽量避免局部最优，又可以根据最优值移动自身，又能节省时间，所以火焰更新的模型如下：

1)火焰F是其对应飞蛾M的历史最优解。

2)每一代火焰更新后，会根据其适应度值，按照从大到小的顺序排列，所以第一只飞蛾总是会根据适应度最好的值更新。

3)为了节省开销，飞蛾和火焰的数量会根据运行的代数不同，不断减少，但飞蛾和火焰的数量始终相同，该函数公式为：

flame_no=round(N-L(N-1)/T)

(8)

其中：N为初始火焰数量，T为迭代的总次数，L为当前迭代次数。

MFO算法的流程：

1)用式(2)初始化飞蛾种群M,根据M计算出适应度值OM；

2)M、OM的位置不变，对M、OM排序得到火焰F和其适应度值OF；

3)根据式(8)求出飞蛾的数量，去掉末尾的飞蛾和火焰；

4)用式(7)求出飞蛾与其对应火焰的距离Di；

5)将Di代入到式(6)中，计算出每只飞蛾更新之后的值；

6)根据M计算出适应度值OM；

7)判断是否达到结束条件，否则跳转到第2)步。

1.2 粒子群优化算法

PSO算法是在由Reynolds等通过鸟类集体飞行捕食得到的启发，整个鸟群好像在一个中心的控制下移动，假设整个区域中只有一个地方有食物，那么找到事物最简单的办法就是向着离事物最近的鸟移动。现将空间中的鸟假设成一个粒子，每个粒子既有社会认知能力也有自我认知能力，社会认知能力及整个种群中最优解，自我认知能力及个体到目前位置的最优解，每个粒子都会随机地向着种群中的最优解和该个体的历史最优解移动，每只飞蛾的每个维度都有自己的速度Vi=(vi1,vi2,…,vij)T和移动距离Xi=(xi1,xi2,…,xij)T,移动速度和移动距离的更新公式如下所示：

vij=vij+c1rand(pbestij-xij)+c2rand(gbestj-xij)

(9)

xij=xij+vij

(10)

学习因子c1、c2一般位于[0,2]内，rand为位于[0,1]的随机数，pbest为历史最优解，gbest为全局最优解。

PSO算法的流程如下：

1)初始化种群随机位置，种群N和其速度V；

2)评价每个微粒的适应度；

3)对所有微粒，将它当前适应度值对比其历史最优适应度值，如果较好，将其作为粒子的历史最优适应度值pbest；

4)对所有粒子，将它当前适应度值对比全局最优适应度值，如果较好，将其作为粒子的全局最优适应度值gbest；

5)将得到的pbest和gbest代入式(9)中得到速度V；

6)将速度V代入到式(10)中得到新的位置；

7)未达到结束条件则转第2)步。

2 融合粒子群的二进制飞蛾扑火优化算法

2.1 提出的融合算法

在二进值群体优化算法中要考虑到平衡算法的局部搜索能力和算法的全局搜索能力。飞蛾扑火优化算法的原理是利用每只飞蛾只围绕着自己所对应的火焰做螺旋飞行运动以寻找最优解，有较强的局部搜索能力，但是全局搜索能力较弱。

考虑到应用于网络入侵检测的特征优化时，MFO算法全局搜索能力差、易陷入局部最优，通过融合PSO算法，以获取更好的全局搜索能力。在此基础上，本文提出融合粒子群的飞蛾扑火优化(Moth-Flame Optimization integrated with Particle swarm optimization, PMFO)算法。

MFO中飞蛾的更新方式是以每只飞蛾围绕火焰螺旋飞行的方式找最优解MFO中每只飞蛾只收敛于自己所对应的火焰一点，这样不仅局部搜索能力差，而且易陷入局部最优, 所以让飞蛾先向全局最优解F1(由于每次迭代火焰F都会按照适应度值从大到小排序，所以F1为全局最优解)和每个粒子所对应的火焰Fi(火焰Fi为第i个飞蛾的历史最优解)的方向移动，再用式(6)作局部搜索，使飞蛾的搜索范围加大，效果更好。PSO改进MFO算法改进公式如下：

PMFO与MFO相比飞蛾的位置更新方式不同，每只飞蛾都对应着自己的速度Vi=(vi1,vi2,…,vij)T，速度更新公式如下：

vij=vij+c1rand(Fij-xij)+c2rand(F1j-xij)

(11)

其中：Fij为中每只飞蛾的历史最优解，F1j为到这一代为止的所有飞蛾的历史最优解。飞蛾先向Fij和F0j的方向移动，更新公式如下：

Mij=vij+Mij

(12)

这时飞蛾已经向前飞行了一段距离，之后再用飞蛾更新后的位置求与火焰之间的距离Di，公式如下：

Di=|Fj-Mi|

(13)

飞蛾M对应火焰的距离螺旋飞行的方式寻找最优解。

Mij=Di·ebtcos(2πt)+Fij

(14)

2.2 种群初始化

在二进制算法中，粒子特征的值只能为0或1，1代表这项特征被选中，0则代表未选中。一般情况，特征有50%的几率被选中是种群初始化的常用方法，被选中粒子的初始化函数如下：

(15)

2.3 飞蛾移动改进

如果对PMFO中飞蛾更新的结果直接进行二进制转换会导致速度影响过大或者距离Di影响过大，从而导致飞蛾更新处于停止状态，所以PMFO的飞蛾的距离更新公式(15)改成如下:

Di=|Fi-Mi|/numAttribute

(16)

其中numAttribute为特征的数量。为了缓解PMFO中速度过大的影响，对速度V设置上限和下限Vmax和Vmin。

2.4 二进制转化

为了解决上述算法在二进制空间中的位置更新问题，本文使用sigmoid函数将飞蛾更新后的实数值映射到[0,1]内，来实现飞蛾位置的“0”和“1”转换。二进制转换公式如下：

(17)

(18)

其中：Mij为飞蛾更新后的位置，rand是[0,1]内的随机数。

2.5 适应度函数

特征优化的目的是去掉以一些对结果影响不大或者是对结果判断有负面影响的特征，以达到提高速度和正确率的目的，所以粒子适值求解步骤如下：

先找到个体特征中为0的值，在数据集中将这些属性都去掉，再将数据放到分类器中求出正确率accuracy。传统方法直接将accuracy作为适应度值，本文使用文献[15]提出的一种适应值求解方法，适应度函数如下：

(19)

其中：λ为特征数量,accuracy为正确率，fitness为飞蛾的适应度值。

2.6 二进制算法流程

融合粒子群的二进制飞蛾扑火优化(Binary Moth-Flame Optimization integrated with Particle swarm optimization，BPMFO)算法的流程描述如下。

1)用式(15)初始化飞蛾种群M,根据M计算出适应度值OM；

2)M、OM的位置不变，对M、OM排序得到火焰F和其适应度值OM；

3)根据式(8)求出飞蛾的数量，去掉末尾的飞蛾和火焰；

4)用式(11)更新飞蛾速度V，如果速度越界，则速度为Vmax或Vmin；

5)已知速度V，用式(12)更新飞蛾F位置；

6)将更新后的飞蛾位置代入式(16)中，求出飞蛾与其对应火焰的距离Di；

7)用式(14)计算出每只飞蛾更新之后的值；

8)用式(17) 、(18)将飞蛾更新后的值转化为二进制；

9)根据M代入到分类器中得到正确率accuracy,将得到的accuracy代入到式(19)中，计算出适应度值OM；

10)判断是否达到结束条件，否则跳转到第2)步。

3 仿真实验

仿真实验考虑将提出的二进制粒子群改进飞蛾扑火优化BPMFO算法与二进制飞蛾扑火优化(Binary Moth-Flame Optimization, BMFO)算法、二进制粒子群优化(BPSO)算法、二进制遗传算法(Binary Genetic Algorithm, BGA)、二进制布谷鸟搜索(BCS)算法，二进制灰狼优化(BGWO)算法进行对比实验，分别使用支持向量机(Support Vector Machine, SVM)[17]、K最近邻(K-Nearest Neighbors,KNN)算法[18]和朴素贝叶斯分类器(Naive Bayes Classifier, NBC)[19]分类，得到最后的实验结果。实验环境为Window7 操作系统，处理器为 Intel Core i7-3630QM CPU 2.40 GHz，内存为4.00 GB，程序用Java编写。

3.1 数据初始化

实验数据采用网络入侵中常用数据集KDD CUP 99 数据集，KDD CUP 99 分为测试集和训练集，一共大约有500万条数据，本文使用其中测试集大约10%数据，在50万条数据集中抽取5 000条数据，其中一半归为训练集一半归为测试集，将数据集中的攻击类型都归为abnormal类，其他数据类型归为normal类。数据一共包含有41维特征，其中3个字符串特征，38个数值型特征[20]。实验中，先对数据进行预处理，将字符串特征对应成数值特征，再对数据集进行0-1标准化处理，处理公式如下：

(20)

其中：v为当前数值，mA为该列最小值，MA为该列最大值，v′为更新后的数值。

3.2 实验结果与分析

实验中各种算法初始种群数量为10，最大迭代次数为50，实验中参数说明如表1中所示。

表1 各种算法参数设置

表2～4分别记录着3种分类器6种算法，仿真实验运行20次的结果。

表2 SVM分类器的实验结果

图1为在3种分类器下6种算法对应的适应度曲线。其中最优适应度值、最差适应度值、平均适应度值主要衡量算法的效果，标准差主要衡量算法的稳定性，运行时间主要衡量算法的运行效率，适应度曲线主要衡量算法的收敛性和跳出局部最优的能力。

实验1用Wake[21]工具箱中的SVM作为分类器，其中向量机种类为分类向量机，核函数类型为高斯函数，核函数中的gamma函数值为1.0，即向量机种类为分类向量机，核函数类型为高斯函数，核函数中的gamma函数值为1.0，其他参数为默认参数。

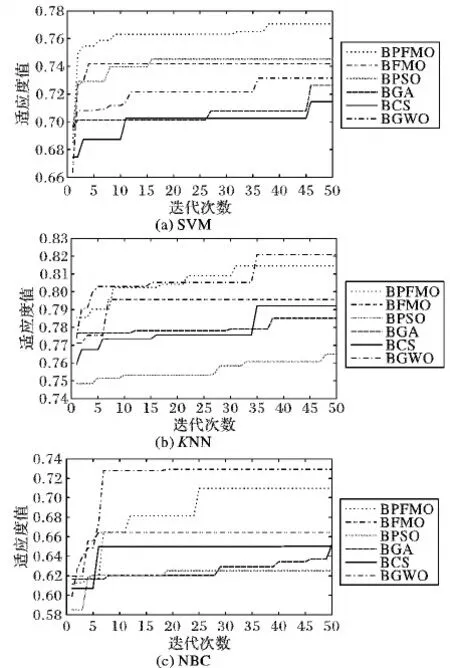
图1 6种算法通过SVM、KNN和NBC三种分类器的适应度值比较

在实验1中，BPMFO在最优适应度值、最差适应度值、平均适应度值和标准差优于其他二进制优化算法，也更加稳定。虽然运行时间比BCS算法长38 s，但是最优适应度值、最差适应度值、平均适应度值比BCS多约0.062、0.078和0.088。BPMFO相对于原MFO算法更易跳出局部最优，实验中的求解效果也优于其他算法(如表2和图1(a)所示)。

实验2用Wake工具箱中的KNN作为分类器，其中参数K=10，即离待测点最近的10个的点参与投票分类。

在实验2中，BPMFO的最优适应度值、最差适应度值、平均适应度值略低于BGWO，但时间上缩短了约230 s。在算法稳定性方面略低于BMFO和BPSO，但在算法效果和运行效率方面优于这两种算法。BPMFO运行时间比BCS多约30 s，但在最优适应度值、最差适应度值、平均适应度值比BCS高约0.010、0.042、0.025，方差也只有BCS的一半。BPMFO相对于其他算法收敛性适中，且具有一定跳出局部最优的能力(如表3和图1(b)所示)。

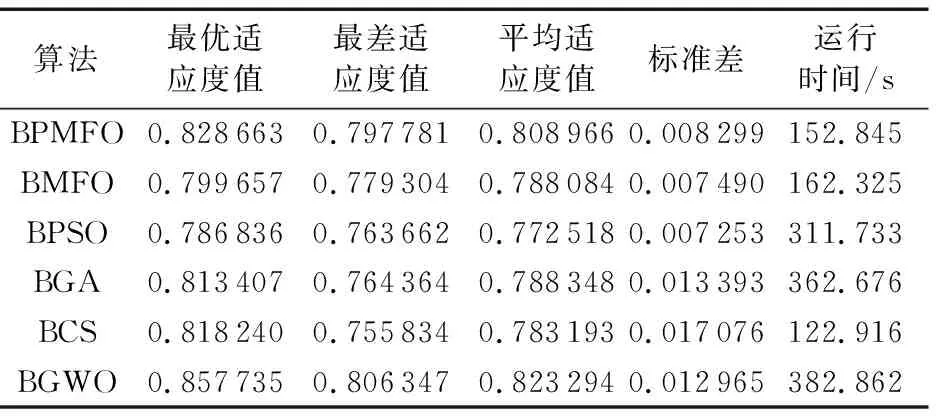
表3 KNN分类器的实验结果

实验3用Wake工具箱中的朴素贝叶斯作为分类器。实验3中，BPMFO的最优适应度值高于BGWO，但最差适应度值、平均适应度值略低于BGWO，但运行时间比BGWO短约12.4 s。在算法稳定性方面略低于BMFO和BPSO，但在最优适应度值、最差适应度值、平均适应度值和运行效率方面比BMFO和BPSO高。虽然在时间上比BCS低0.7 s，但是最优适应度值、最差适应度值、平均适应度值比BCS高约0.023、0.032、0.027，并且在算法稳定性上优于BCS算法。BPMFO相对于其他算法收敛性适中，具有一定跳出局部最优的能力、且实验的求解效果略低于BGWO，但优于其他算法(如表4和图1(c)所示)。

表4 Naive Bayes分类器的实验结果

3.3 实验结论

本节使用了BPMFO、BMFO、BPSO、BGA、BCS、BGWO共6种优化算法，分别采用SVM、KNN、NBC三种分类器进行仿真实验。实验证明了提出的BPMFO算法具有较好的求解能力，相对于传统PSO、遗传算法(Genetic Algorithm, GA)来说运行时间大幅度缩减，虽然在实验2和实验3中，求解效果低于BGWO，但是运行时间只有BGWO的1/3，相对于原MFO算法，改进原算法易陷入局部最优并且收敛过快的缺陷，在算法求解能力上也有所提升，同时BPMFO也具有相当不错稳定性，应用于网络入侵检测中有很好的效果。