探究一类“蚂蚁觅捷径”问题

■徐照武

在立体几何的实际应用中,我们经常会遇到一类融知识性和趣味性于一体的“蚂蚁觅捷径”问题,解决这类问题的关键是展开空间几何体,化立体问题为平面问题,进而运用勾股定理来解决,下面举例说明。

题目 如图1,一只蚂蚁要从棱长为1的正方体的一个顶点A沿着表面爬到与它相距最远的另一个顶点G。设蚂蚁爬行的最短路程是d,则d2是多少?

分析：解答“蚂蚁觅捷径”问题最关键的是确定最短爬行路线。对于此题,有的同学可能会认为最短路程是AF+FG、AB+BG、AE+EG或AH+HG,但这些都是错误的。我们应该把正方体沿棱FG,GC,BC剪开,使面BCGF与面ABFE在同一个平面内,然后利用勾股定理计算A,G两点之间的距离d。

解：把正方体沿棱FG,GC,BC剪开,使面BCGF与面ABFE在同一个平面内,如图2所示。

图2

由图2可知最短路程就是Rt△ACG的斜边AG的长(两点之间线段最短)。

设蚂蚁爬行的最短路程是d。

由勾股定理可得d2=AG2=AE2+EG2=12+22=5。

评注:本题的路线不止一条,你还能再找出来吗?不难发现,若正方体的棱长为a,蚂蚁爬行的最短路程是d,则d2=5a2。

变式1：一群蚂蚁在如图3所示的长方体ABCD-A1B1C1D1的点C1处筑了一个窝,该长方体的长,宽,高分别为AB=3,BC=4,CC1=5。一只蚂蚁从点A沿长方体表面爬行回窝,蚂蚁回窝有最短路线吗?请你找出来。

图3

提示：解答此题,可对长方体表面进行剪开铺平求解。究竟哪条线路最短,应逐一解答再比较得出。

①把面ABB1A1与面A1B1C1D1展开成一个平面,如图4所示。在直角三角形ABC1中,AB=3,BC1=BB1+B1C1=5+4=9,由勾股定理可得AC21=32+92=90。

图4

②把面ABB1A1与面BCC1B1展开成一个平面,如图5所示。在直角三角形ACC1中,CC1=5,AC=AB+BC=3+4=7,由勾股定理可得AC21=72+52=74。

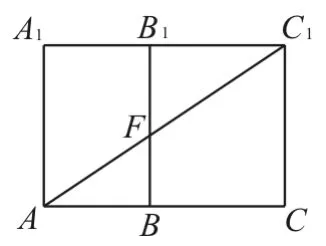
图5

③把面ABCD与面BCC1B1展开成一个平面,如图6所示。在直角三角形AB1C1中,B1C1=4,AB1=AB+BB1=3+5=8,由勾股定理可得=82+42=80。

图6

由于74＜80＜90,故可知图5中的AC1是最短线路,即蚂蚁可以先在面ABB1A1内由A到F,再在面BCC1B1内由F到C1。

变式2：如图7所示,一只蚂蚁绕圆柱一周从母线AB的端点A爬到B点。若圆柱的高为3π,底面半径为2,求蚂蚁爬行的最短路程。

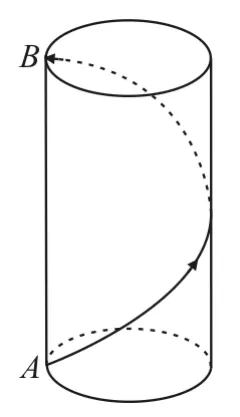
图7

提示：将圆柱侧面沿母线AB剪开成一个平面,如图8所示,则蚂蚁沿图8中的路线AB"爬行是最短路程。

图8

在Rt△AA"B"中,AA"=2π×2=4π,AB=A"B"=3π,由勾股定理可得AB"=