点、直线、平面之间的位置关系综合演练B卷

■吴传叶

一、选择题

1.已知平面α和直线l,则α内至少有一条直线与l( )。

A.平行 B.相交

C.垂直 D.异面

2.已知a,b,c为三条不重合的直线,现有下列结论:①若a⊥b,a⊥c,则b∥c;②若a⊥b,a⊥c,则b⊥c;③若a∥b,b⊥c,则a⊥c。其中正确结论的个数为( )。

A.0 B.1

C.2 D.3

3.若空间中n个不同的点两两之间的距离都相等,则正整数n的取值( )。

A.至多等于3 B.至多等于4

C.等于5 D.大于5

4.如图1,平面α∩β=l,点A,B∈α,点C∈β,且点C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )。

A.点A B.点B

C.点C但不过点M D.点C和点M

5.已知a,b,c为三条不同的直线,且a⊂平面α,b⊂平面β,α∩β=c。

现有下列四个命题:

①若a与b是异面直线,则c至少与a,b中的一条相交;

②若a不垂直于c,则a与b一定不垂直;

③若a∥b,则必有a∥c;

④若a⊥b,a⊥c,则必有α⊥β。

其中正确命题的个数是( )。

A.0 B.1

C.2 D.3

6.设a,b是互不垂直的两条异面直线,则下列命题成立的是( )。

A.存在唯一直线l,使得l⊥a,且l⊥b

B.存在唯一直线l,使得l∥a,且l⊥b

C.存在唯一平面α,使得a⊂α,且b∥α

D.存在唯一平面α,使得a⊂α,且b⊥α

7.如图2,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )。

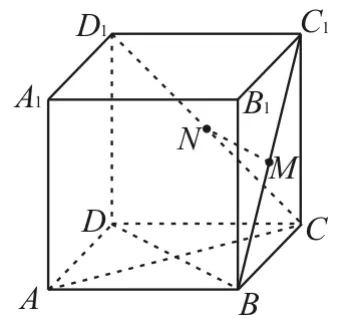
图2

A.MN与CC1垂直

B.MN与AC垂直

C.MN与BD平行

D.MN与A1B1平行

8.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( )。

A.m∥α,n∥α,则m∥n

B.m∥n,m∥α,则n∥α

C.m⊥α,m⊥β,则α∥β

D.α⊥γ,β⊥γ,则α∥β

9.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )。

A.若α⊥β,m⊂α,n⊂β,则m⊥n

B.若m⊥α,m∥n,n∥β,则α⊥β

C.若m⊥n,m⊂α,n⊂β,则α⊥β

D.若α∥β,m⊂α,n⊂β,则m∥n

10.设l是直线,α,β是两个不同的平面,则下列说法正确的是( )。

A.若l∥α,l∥β,则α∥β

B.若l∥α,l⊥β,则α⊥β

C.若α⊥β,l⊥α,则l∥β

D.若α⊥β,l∥α,则l⊥β

11.如图3,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF,则下列结论不正确的是( )。

图3

A.CD∥平面PAF

B.DF⊥平面PAF

C.CF∥平面PAB

D.CF⊥平面PAD

12.已知m,n为异面直线,m⊥平面α,n⊥平面β。直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( )。

A.α∥β且l∥α

B.α⊥β且l⊥β

C.α与β相交,且交线垂直于l

D.α与β相交,且交线平行于l

13.设a,b是两条不同的直线,α,β是两个不同的平面,则能得出a⊥b的是( )。

A.a⊥α,b∥β,α⊥β

B.a⊥α,b⊥β,α∥β

C.a⊂α,b⊥β,α∥β

D.a⊂α,b∥β,α⊥β

14.a,b,c表示不同的直线,M表示平面,给出下列四个命题:

①若a∥M,b∥M,则a∥b或a,b相交或a,b异面;②若b⊂M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b。

其中正确的命题是( )。

A.①④ B.②③

C.③④ D.①②

15.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( )。

A.若α⊥γ,α⊥β,则γ∥β

B.若m∥n,m⊂α,n⊂β,则α∥β

C.若m∥n,m⊥α,n⊥β,则α∥β

D.若m∥n,m∥α,n∥β,则α∥β

16.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:

①若m∥l,且m⊥α,则l⊥α;

②若m⊥l,m⊥α,则l∥α;

③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;

④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m。

其中正确命题的个数是( )。

A.1 B.2

C.3 D.4

17.如图4,在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB,BC,SC,SA交于点D,E,F,H。D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为( )。

图4

18.如图5,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么点D在平面ABC内的射影点H必在( )。

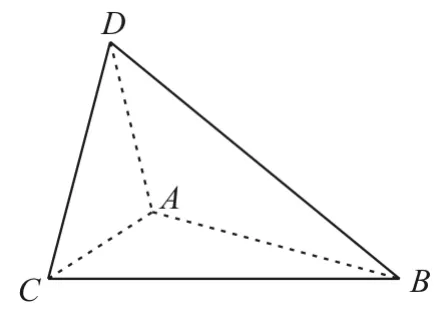
图5

A.直线AB上 B.直线BC上

C.直线AC上 D.△ABC内部

19.已知长方体ABCD-A1B1C1D1中,AA1=3,AB=4,若在棱AB上存在点P,使得D1P⊥PC,则AD的取值范围是( )。

A.(0,1] B.(0,2]

20.如图6所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )。

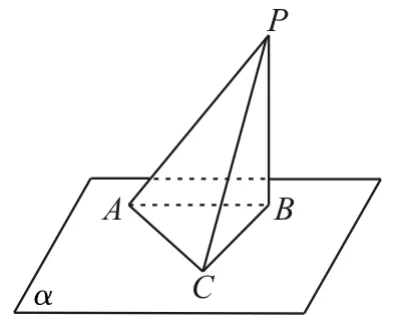
图6

A.一条线段

B.一条直线

C.一个圆

D.一个圆,但要去掉两个点

21.如图7所示,在四面体ABCD中,截面PQMN是正方形,则在下列结论中,错误的是( )。

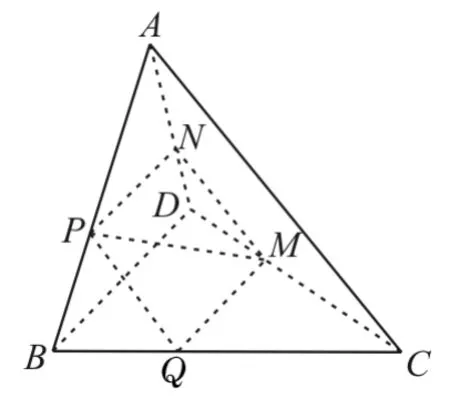
图7

A.AC⊥BD

B.AC∥截面PQMN

C.AC=BD

D.异面直线PM与BD所成的角为45°

二、填空题

22.设a,b为不重合的两条直线,α,β为不重合的两个平面,给出下列命题:

①若a⊂α,b⊄α,a,b是异面直线,那么b∥α;

②若a⊂α,b∥α,a,b共面,那么a∥b;

③若α∥β,a⊂α,则a∥β。

上面命题中,所有真命题的序号是____。

23.将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”。给出下列四个命题:

①垂直于同一平面的两直线平行;

②垂直于同一平面的两平面平行;

③平行于同一直线的两直线平行;

④平行于同一平面的两直线平行。

其中是“可换命题”的是____。(填序号)

24.已知直线a,b,c,现有下面四个命题:

①若a,b异面,b,c异面,则a,c异面;

②若a,b相交,b,c相交,则a,c相交;

③若a∥b,则a,b与c所成的角相等;

④若a⊥b,b⊥c,则a∥c。

其中真命题的序号是____。

25.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则____(写出所有正确结论的编号)。

①四面体ABCD每组对棱相互垂直;

②四面体ABCD每个面的面积相等;

③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;

④连接四面体ABCD每组对棱中点的线段相互垂直平分;

⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长。

26.如图8,在三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形。

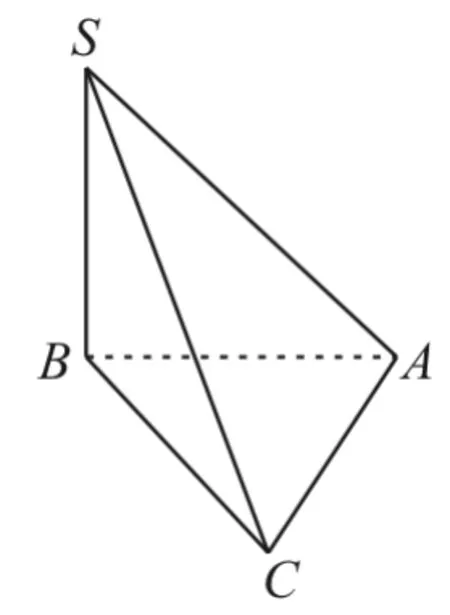
图8

现有以下结论:

①异面直线SB与AC所成的角为90°;

②直线SB⊥平面ABC;

③平面SBC⊥平面SAC;

其中正确结论的序号是____。

三、解答题

27.如图9,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M为AD的中点,N为PC上一点,且PC=3PN。

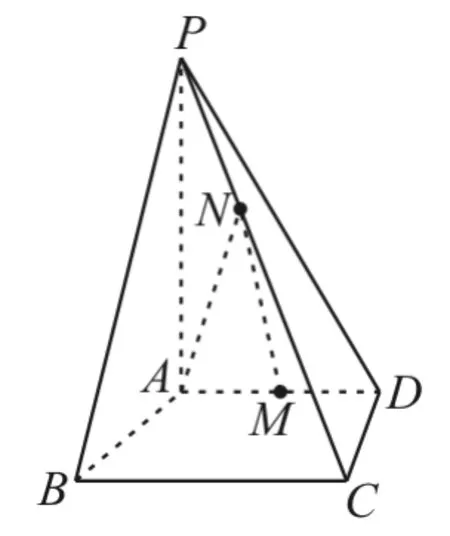
图9

(1)求证:MN∥平面PAB。

(2)求点M到平面PAN的距离。

28.如图10,正方形ABCD和直角梯形ACEF所在的平面互相垂直,FA⊥AC,EF∥AC,AB=2,EF=FA=1。

图10

(1)求证:CE∥平面BDF。

(2)求证:BE⊥平面DEF。

29.如图11,已知正四棱柱ABCDA1B1C1D1,M是DD1的中点。

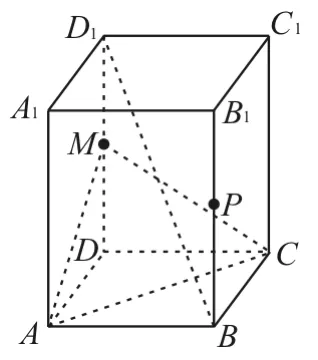
图11

(1)求证:BD1∥平面AMC。

(2)求证:AC⊥BD1。

(3)在线段BB1上是否存在点P,当=λ时,平面APC∥平面AMC?若存11在,求出λ的值,并证明;若不存在,请说明理由。