大尺度模拟二维晶粒长大过程的相场法研究
2018-12-13梁冬梅张义灵罗志荣
梁冬梅,李 洁,张义灵,罗志荣
(玉林师范学院 物理科学与工程技术学院,广西 玉林 537000)
0 前言
多晶材料中晶粒长大过程控制着微观组织结构的演变,而晶粒组织结构直接影响着材料性能[1],研究多晶材料晶粒长大过程中晶粒尺寸、边数的变化以及单个晶粒长大动力学具有重要意义。
传统上对晶粒长大的研究主要集中在理论和实验两方面[2]。随着科学技术与计算机技术的快速发展,出现了许多计算机模拟晶粒长大的方法,如蒙特卡罗(MC)[3-5]、元胞自动机(CA)[6]和相场(PF)[7]等方法。孙亚等人[8]采用相场法对二维晶粒长大过程进行仿真,研究了晶粒尺寸分布与拓扑演变;花福安等人[9]结合晶粒长大速率的统计理论,采用CA方法对基于曲率驱动机制的晶粒长大过程进行了研究;罗志荣等人[10]采用相场法探讨了不同初始微结构(柱状和梯度)对晶粒长大过程及其长大动力学的影响;Zöllner和Rios[11]采用MC方法模拟了二维晶粒长大过程中3种经典拓扑转变以及单个晶粒长大轨迹。上述研究采用了不同的方法模拟晶粒长大过程,但其模拟尺度均较小。实际上,模拟尺度越大,数据离散程度越小,获得的晶粒长大动力学和尺寸分布越准确[12]。然而,目前大尺度模拟二维晶粒长大过程中的晶粒半径和边数分布以及单个晶粒长大动力学的相场法研究还鲜有报道。相场法在模拟晶粒长大过程中对晶界做弥散化处理,不必直接跟踪动态界面,且易于将物理场等因素对晶粒长大的影响考虑进来,物理意义更明确[2]。故本研究采用相场法大尺度模拟二维晶粒长大过程,从动力学角度研究晶粒长大的特征并定量分析晶粒长大过程中相对晶粒半径、晶粒边数的分布特点,揭示二维晶粒长大的规律。
1 理论模型
1.1 相场模型
在相场模型中,用场变量ηi(r,t)(i=1,2,…,p)表示多晶材料内不同晶粒的取向,其中p是晶粒取向个数,ηi(r,t)是空间位置r和时间t的连续函数。在任意晶粒内部,其场变量的绝对值,其余场变量 ηj≠i=0;在晶界处,在0~1之间连续变化,形成弥散界面。系统总自由能函数F由场变量及其梯度项表示为[13]
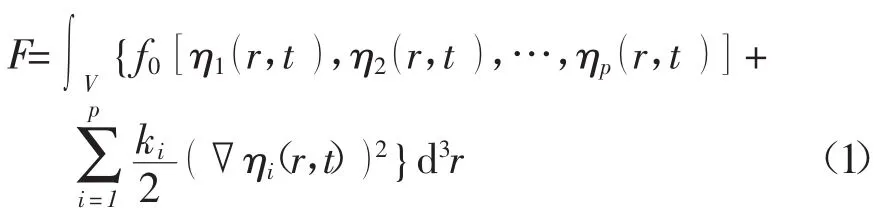
式中 ki为梯度能系数,与界面能有关;f0为局部自由能密度函数,表示为[13]:
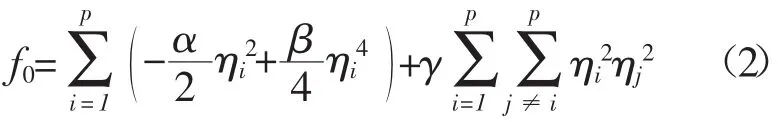
式中 α、β和γ为正实数,γ>β/2。
由于取向场变量为非保守场变量,根据Ginzburg-Landau(弛豫)方程可得取向场变量在空间与时间上的演化公式为[13]:

式中 Li为弛豫系数,与晶界迁移率有关。
在时间上,对动力学方程式(3)使用显式Euler迭代公式可得[13]
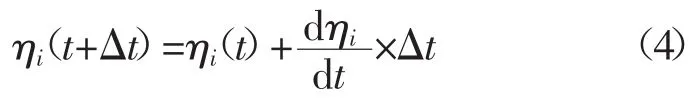
式中 Δt为离散时间步。另外,在空间上,对取向场变量的Lapace算子操作处理到次近邻格点[13]
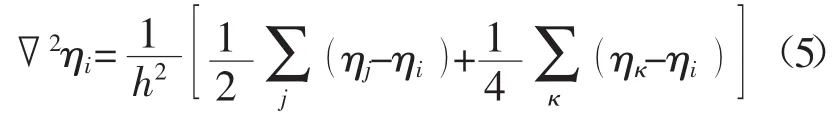
式中 h为空间步长;j与κ分别为i的最近邻和次近邻格点。
1.2 参数设置
本研究模拟二维正常晶粒长大过程,界面能和晶界迁移率均为各向同性。仿真时将连续区域离散为四方格点,选取4 096×4 096的二维矩阵,采用周期性边界条件。场变量的初值取[-0.001,0.001]之间的随机数,晶粒取向个数p=36。其他参量设置为α=β=γ=1.0,ki=2.0(界面能各向同性),Li=1.0(晶界迁移率各向同性),Δt=0.25,h=2.0。计算过程中对系统所有格点尝试1遍后计为1个模拟时间步(ts),最终模拟出整个晶粒的长大过程。
2 模拟结果与分析
2.1 晶粒半径与边数分布规律
在晶粒长大过程中,系统晶粒个数由71 140个(t=1 000 ts)逐渐减少至 10 276个(t=10 000 ts)。统计这些晶粒,得到不同演化时间的相对晶粒半径分布曲线,如图1所示。由图1可知,随着时间的增加,相对晶粒半径分布的最大频率始终在R/Rc=1附近;而 R/Rc<0.2,R/Rc>2 出现的频率较低,即半径偏大或偏小的晶粒较少,且没有出现异常大(R/Rc>2.5)的晶粒。说明系统中晶粒半径分布均匀,晶粒长大符合正常晶粒长大规律。还可以看出,不同演化时间的相对晶粒半径分布曲线相似度较高,说明相对晶粒半径分布具有自相似性,这与采用相同方法模拟得到的结果[8]相比,本研究大尺度统计得到的相对晶粒半径分布较稳定,结果更加精确。
不同演化时间的晶粒边数分布曲线如图2所示。由图2可知,系统中五边形晶粒出现频率最高,六边形晶粒仅次之,边数小于3和大于9的晶粒出现频率较低,晶粒边数绝大部分分布在4~8之间。不同演化时间的晶粒边数分布曲线非常相似,分布频率相对稳定,说明晶粒边数分布具有时间不变性(自相似性),与采用CA方法模拟的结果[14]一致。
不同演化时间的晶粒边数与晶粒半径的关系曲线如图3所示。晶粒半径表示所有边数相同的晶粒半径的平均值。由图3可知,晶粒边数与晶粒半径呈正相关,在同一演化时间,晶粒边数越大,晶粒半径越大;随着演化时间的增加,晶粒半径也随之增大,且演化时间越长,晶粒半径随边数增加得越快。

图1 不同演化时间的相对晶粒半径分布
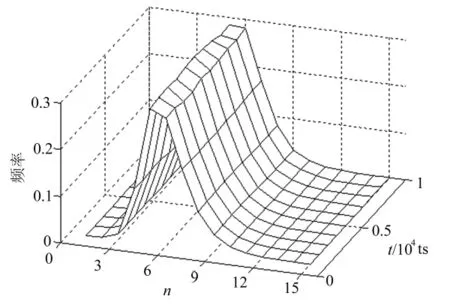
图2 不同演化时间的晶粒边数分布
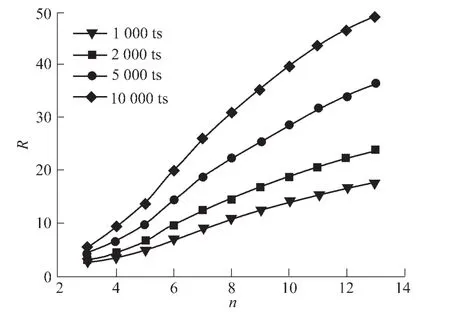
图3 不同演化时间的晶粒边数与晶粒半径的关系
2.2 单个晶粒长大动力学
晶粒长大是大晶粒不断吞噬近邻小晶粒的过程。为了探究晶粒长大规律,有必要对单个晶粒的半径与边数进行研究,Hillert提出单个晶粒长大速率的理论方程为[15]
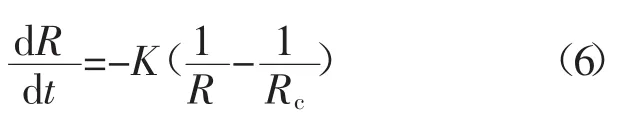
式中 K为一个正常数;R为单个晶粒的半径;Rc为临界晶粒半径(二维网格下系统的平均晶粒半径)。根据式(6)在二维网格下晶粒半径大于临界半径的晶粒(大晶粒)趋于长大,反之亦然。本研究对dR/dt的计算使用有限差分近似[16]
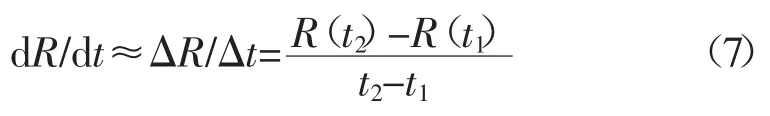
式中 t1和t2分别为 2 000 ts和2 010 ts,Δt=10 ts。统计2 010 ts时系统中41 845个晶粒的增长率与半径、边数的关系,结果如图4和图5所示。

图4 晶粒增长率与晶粒半径的关系
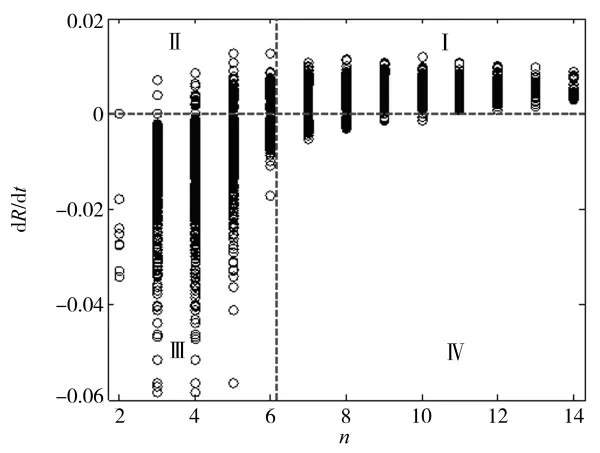
图5 晶粒增长率与晶粒边数的关系
晶粒增长率与半径的关系如图4所示。图4可分为 4 个区域,分别是Ⅰ区域(1/R-1/Rc>0,dR/dt>0)、Ⅱ区域(1/R-1/Rc≤0,dR/dt≥0)、Ⅲ区域(1/R-1/Rc<0,dR/dt<0)和Ⅳ区域(1/R-1/Rc≥0,dR/dt≤0),各区域分布频率分别是7.58%、34.21%、4.37%和53.84%。由图可知,系统中小晶粒居多且绝大部分小晶粒趋于缩小,绝大部分大晶粒趋于长大;在1/R-1/Rc=0附近晶粒分布密度最高,增长率趋于0,晶粒变化不明显;半径接近临界半径的晶粒,增长率越慢;晶粒半径越小,增长率变化范围越大,具有负增长率的小晶粒,其半径越小,负增长率越大,说明半径越小的晶粒越容易被周围大晶粒吞噬。在Ⅱ、Ⅳ区域,仿真数据与Hillert理论方程吻合较好,半径大于临界半径的晶粒趋于长大,半径小于临界半径的晶粒趋于收缩;在Ⅰ、Ⅲ区域,仿真数据与Hillert理论方程存在差异,这部分晶粒占11.95%。可见,在一定误差范围内晶粒长大速率与Hillert理论方程吻合,这与采用CA方法仿真结果[17]一致。
晶粒增长率与边数的关系如图5所示。图5也可以分为 4 个区域:Ⅰ区域(n>6,dR/dt≥0)、Ⅱ区域(n≤6,dR/dt≥0)、Ⅲ区域(n≤6,dR/dt<0)和Ⅳ区域(n>6,dR/dt<0)。4个区域的分布频率分别是 29.57%、35.33%、33.88%、1.22%。显而易见,边数大于6的绝大部分晶粒趋于长大,边数小于6的晶粒部分趋于收缩部分趋于长大;边数相同的晶粒,其增长率也不同,这是因为晶粒的长大情况受近邻晶粒的影响,只有在演化过程中一直具有优势的晶粒才能持续长大。边数小于6的晶粒,其增长率波动范围较大,这与图4中晶粒半径越小,晶粒增长率变化范围越大相对应。这是因为晶粒边数与晶粒半径呈正相关,晶粒的边数越小则半径越小。
为进一步研究晶粒长大规律,有必要对不同生长特点的单个晶粒进行研究。在t=1 000 ts时,随机选取9个不同特点的晶粒并监测其面积和边数的变化,如图6所示。图6a为晶粒面积随时间变化的轨迹。可见,随着时间的演化,初始面积较小的晶粒在较短时间内消失了,与图4中晶粒半径越小、负增长率越大、越容易被周围晶粒吞噬的结论相符;而初始面积较大的晶粒,一部分随时间增大而增大,一部分随时间先增大后减小甚至消失,这是由于在晶粒长大过程中,平均晶粒面积(图6a虚线)随时间不断增大,开始时刻比平均晶粒面积大的晶粒,最终的晶粒面积会小于或等于平均晶粒面积,最后甚至消失;在演化初期即使晶粒面积相同,其面积变化的规律也不同,这与晶粒所处环境有关。还可以看到,在开始很短一段时间内,晶粒面积随时间线性变化,这与采用MC方法仿真结果[18]吻合。
图6b为晶粒边数随时间变化的轨迹。可见,随着时间的演化,晶粒边数的变化分为3种情况:先增大后减小、先减小再增大最后减小、一直减小直至消失。然而,无论哪种变化,演化后期的晶粒边数总小于演化初期,这是因为在多晶体系中,曲率驱动晶粒不断长大,晶界不断减小使得总界面自由能减少的缘故。开始时刻边数为7的晶粒最终消失了,与图5中边数大于6的部分晶粒呈负增长的结论相符。

图6 单个晶粒的面积和边数随时间变化的轨迹
从图6中随机选取单个晶粒面积随边数变化的轨迹如图7所示。开始时刻的晶粒边数最大,在晶粒长大过程中,晶粒面积变大,晶粒边数减小;当晶粒面积达到最大时,晶粒边数为6,超过该数据点后,晶粒趋于收缩(见图7b),晶粒边数变为3,最后晶粒消失。可见,在晶粒消失之前,晶粒边数至少为 3,与文献[11,18]的结论一致。
3 结论
(1)采用相场法大尺度模拟晶粒长大过程,得到的相对晶粒半径分布和晶粒边数分布较为稳定,均具有时间不变性;相对晶粒半径分布的最大频率在R/Rc=1附近,晶粒边数绝大部分分布在4~8,并且晶粒边数与半径呈正相关。
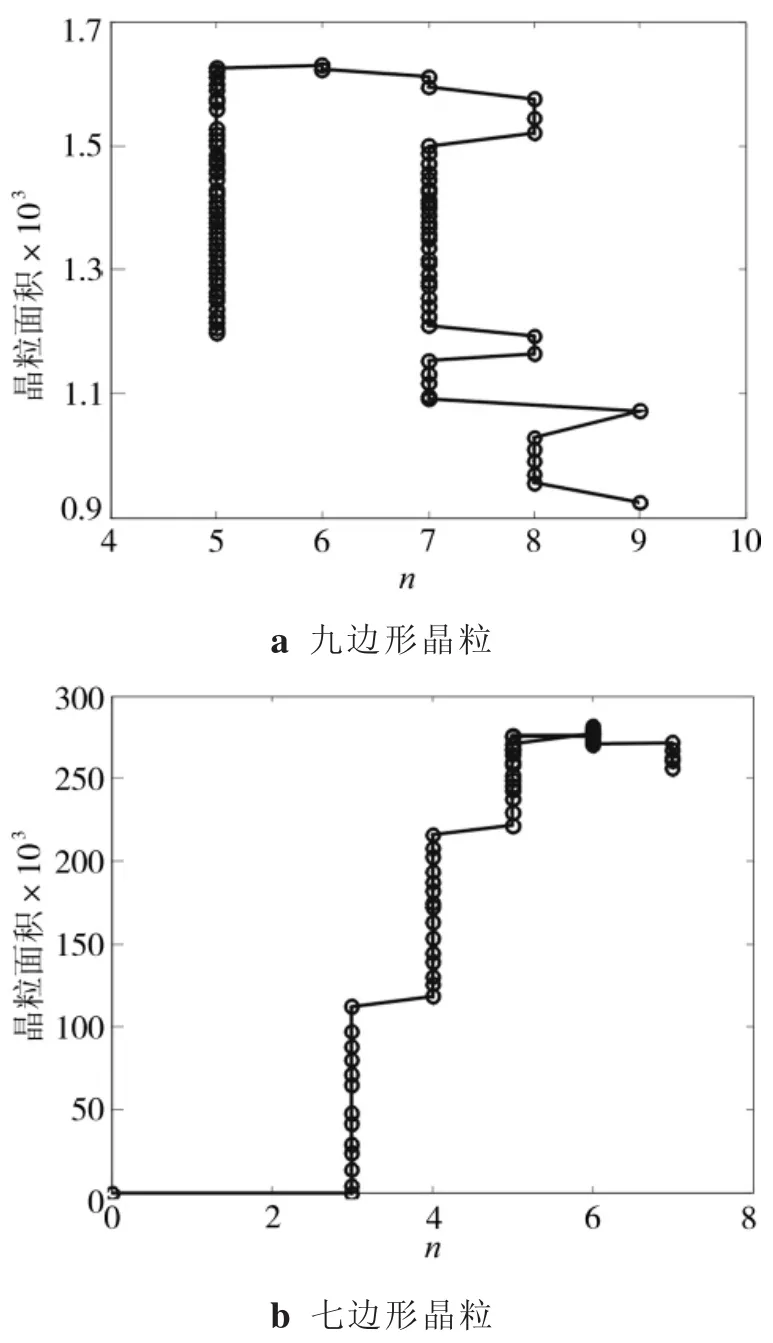
图7 单个晶粒面积随边数变化的轨迹
(2)在单个晶粒长大动力学研究中,边数大于6和半径大于临界半径的绝大部分晶粒会长大,边数小于6的晶粒增长率变化幅度较大,半径小于临界半径的绝大部分晶粒会趋于缩小甚至消失。
(3)在一定误差范围内,单个晶粒长大速率和半径的关系与Hillert理论方程吻合较好。
