S355J2W+N钢对接接头应力集中系数计算及回归分析

孙 杨 ，王福山 ，胡立国 ，张印广 ，杨鑫华

（1.大连交通大学，辽宁大连116028；2.中车长春轨道客车股份有限公司质量保证部，吉林长春130062；3.辽宁省轨道交通装备焊接与可靠性重点实验室，辽宁大连116028；4.广东美的暖通设备有限公司，广东佛山528000）

0 前言

应力集中是焊接结构在服役过程中断裂和疲劳破坏的重要因素之一。在S355J2W+N钢对接接头疲劳试验过程中发现，断裂均发生在焊趾处，并且对于不同焊缝高度和焊缝熔宽的试件，疲劳强度存在差异，影响疲劳试验效率。研究不同焊缝几何参数对接头应力集中的影响规律，对准确计算焊趾处应力集中分布、提高疲劳试验效率具有重要意义。国内外学者对该问题进行了多项研究[1-7]，但计算数据较少，未涉及焊缝熔宽和高度对焊趾处应力集中系数Kt的影响。李栋才[8]等人采用有单侧加强高的对接接头计算模型，考虑了焊趾过渡圆弧半径r和焊趾倾角θ对Kt的影响，给出了估算Kt的经验公式。张毅[9]等人在单侧加强高的对接接头的研究中分析了焊趾倾角、焊趾过渡圆弧半径以及板厚对Kt的影响，得出过渡圆弧对应力集中没有影响，并给出Kt计算公式。

本研究采用有限元法对焊接接头进行应力分析，研究焊缝几何参数对焊趾处应力集中系数Kt的影响。通过模拟计算S355J2W+N钢对接接头不同焊缝几何参数（余高和焊宽）下焊趾处应力集中分布，并通过回归分析建立焊趾处应力集中系数Kt的经验公式，既可为确定疲劳试验载荷、提高疲劳试验效率提供依据，也可为改进焊接接头设计、降低应力集中系数提供支持。

1 有限元模型的建立

疲劳试件的几何尺寸如图1所示。试件加工过程会造成其焊缝熔宽和余高存在差异。为确定不同焊缝熔宽和余高，假设接头焊缝截面规则且左右对称，并且不存在角变形、未焊透等缺陷，不考虑焊趾存在过渡圆弧。为简化模型并准确进行名义应力加载，采用S4即四节点平面壳单元建立不同焊缝参数下的有限元模型，如图2所示。焊趾处网格采取细化处理，最小单元尺寸约为0.25mm×0.4mm，材料的弹性模量 E=2.13×105N/mm2，泊松比为 0.32。

图1 试件的几何尺寸

图2 对接接头有限元模型

为简化应力集中系数的计算过程，模型加载的名义应力为100 MPa，有限元计算的约束与载荷的施加方式如图2所示。模型左端节点施加全约束，右端节点约束除加载方向以外的全部自由度，载荷转换为相应数值的集中力施加于节点上。

2 计算结果及回归分析

利用有限元分析软件ABAQUS对建立的模型进行应力计算，采用的焊缝熔宽W分别为15 mm、16 mm、17 mm、18 mm、19 mm和20 mm，余高H分别为 1 mm、1.5 mm、2.0 mm、2.5 mm 和 3 mm，板厚为12 mm，应力集中系数值按最大主应力计算。所得Mises应力云图和最大主应力云图分别如图3所示（以余高2 mm、焊宽15 mm为例）。由最大主应力计算的应力云图可知，焊趾位置出现应力集中，最大值为145 MPa。采用Mises应力计算的Kt值小于最大主应力计算的Kt值。

最大主应力计算的焊趾应力集中的结果如图4所示。可以看到，当余高H=1.0时，焊缝熔宽由15 mm增加至20 mm，焊趾应力集中系数Kt由1.38降至1.25，降幅为10.79%。同时对应余高H为1.5 mm、2.0 mm、2.5 mm、3.0 mm时，焊趾应力集中系数Kt降幅分别为10.87%、11.39%、10.33%、9.86%。当余高H≤2.0 mm时，余高的增加对焊趾应力集中系数Kt的影响逐渐增大，当2.0 mm＜H≤3.0 mm时，余高的增加对焊趾应力集中系数的影响逐渐减小。图4b为不同焊缝熔宽下焊趾应力集中系数Kt随余高的变化。当焊缝熔宽为15 mm、16 mm、17 mm、18 mm、19 mm、20 mm时，余高由1.0 mm增加至3.0 mm，焊趾应力集中系数Kt增幅分别为32.79%、33.17%、33.10%、33.19%、33.09%、32.70%。相对于焊缝熔宽，余高变化引起的焊趾应力集中系数的变化幅度更大，最高可达33.19%。Kt越小，承载能力越强，因此在设计对接接头时，选择大熔宽、小余高有利于提高接头承载能力。

图3 应力分布云图

图4 应力集中系数Kt随几何参数变化

为了直观反映焊缝熔宽和余高对应力集中因数的共同影响，对焊缝熔宽和余高进行归一化处理，以焊缝熔宽/板厚、余高/板厚为参数因素，绘制二者与应力集中系数的变化关系，如图5所示。

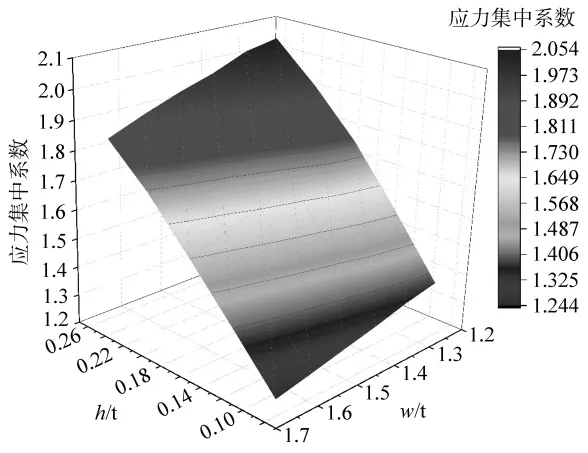
图5 有限元计算几何参数与应力集中系数Kt关系曲面

由图5可知，随着焊缝熔宽的减小和余高的增大，焊缝焊趾处应力集中系数随之增大。采用最大主应力计算的最大应力集中系数为2.054，最小应力集中系数为1.244。对上述所有数据进行非线性拟合，设所用拟合函数通式为

式中 x为余高/板厚，即h/t；y为焊缝熔宽/板厚，即w/t；z为应力集中系数，Kt；A、B、C、D、E 为供迭代所用未知常数。

经过数据迭代，得到常数拟合结果如表1所示。

表1 根据拟合结果获得的供迭代所用未知常数

最终拟合函数为：

拟合公式计算的不同焊缝熔宽和余高自由组合下应力集中系数曲面如图6所示。可以看出，最大应力集中系数为2.060，最小应力集中系数为1.220。对拟合公式计算结果和有限元分析结果进行误差计算对比，大部分误差小于1%，个别情况下误差略大，这是由于W较小时，较大的焊趾过渡半径严重影响接头应力流线形状造成的。误差计算结果如表2所示。

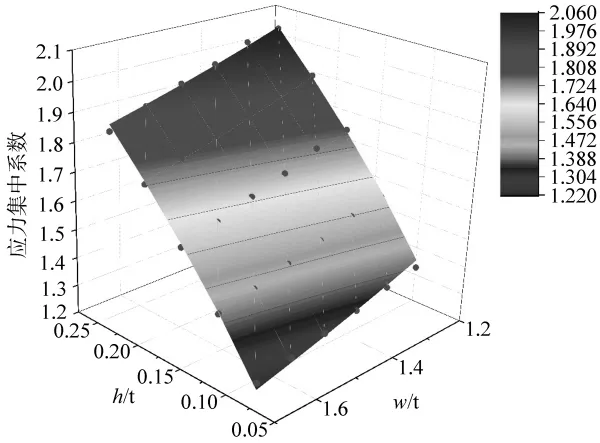
图6 拟合公式计算几何参数与应力集中系数Kt关系曲面

3 结论

（1）应力集中在对接接头焊趾处比较明显，余高变化对焊趾处应力集中影响较大。在相同焊缝熔宽下，焊趾应力集中系数Kt随着余高的增大而增大，最大增幅为33.19%。当1.0 mm≤H≤2.0 mm时，余高增大对应力集中系数Kt的影响逐渐增大，但当2.0 mm≤H≤3.0 mm时，余高增大对Kt的影响呈现减小趋势。

（2）对比焊缝熔宽W和余高H的变化对焊趾处应力集中系数Kt的影响，建立应力集中系数快速计算模型。该模型计算结果与有限元仿真得到的结果相似度较高，为快速确定焊接接头的应力集中系数提供了工具，有利于提高疲劳试验效率，对改善焊趾处应力集中具有现实指导意义。

表2 有限元计算与拟合公式计算误差