基于有限元极限分析法的土坡稳定性分析★

2018-12-11唐超阳

山西建筑 2018年32期

王奇唐超阳

(1.湖南省高速公路建设开发总公司，湖南长沙 431001; 2.湖南大学设计研究院有限公司,湖南长沙 410082)

0 引言

边坡稳定性分析是岩土工程经典的问题之一，随着有限元、有限差分等方法的发展，较好的弥补了传统方法在边坡稳定性分析上的不足。赵尚毅等[1]采用有限元强度折减法对边坡稳定安全系数进行了计算，并得到了各种屈服准则的相互代换关系。邓友生等[2]采用瑞典圆弧条分法和有限元软件ADINA对土坡稳定安全系数进行了计算。姜恒超[3]基于FLAC3D对路基边坡安全系数的影响因素进行了分析。以上有限元、有限差分法需要反复迭代得到计算结果，在计算效率上还可进一步提升。最近发展起来的有限元极限分析法可以克服以上方法的不足[4]。因此，本文将根据极限分析和有限元的基本原理，基于MATLAB编制相关计算程序，对土质边坡的稳定性进行分析。

1 有限元极限分析法简介

有限元极限分析法是在传统极限分析法的基础上，将寻找运动许可的速度场和静力许可的应力场转化为相应的数学规划问题，然后利用MATLAB的优化算法对数学规划模型进行求解，最终得到上、下限解。根据文献[4]，求解的步骤如图1所示。

2 问题的描述

本文假定边坡坡面水平，边坡高度为H，坡角为β，将其视为平面应变问题，土体的粘聚力和内摩擦角分别为c,φ，符合摩尔—库仑屈服准则，计算模型如图2所示。

根据文献[4]，本文上、下限分析均采用三角形单元，单元总数为6 000，并采用网格自适应技术，分三次迭代。模型左右边界的法向位移为0，底边完全固定，其他边界为自由边。取β=45°为例，其网格划分效果及边界条件如图3所示。

边坡稳定安全系数有两种确定方法，分别为强度折减法和重度增加法。本文采用重度增加法来计算边坡稳定安全系数。重度增加法为边坡土体的材料参数保持不变，重度逐渐增加，直到边坡发生失稳破坏。采用重度增加法所得安全系数F可表示为：

F=γc/γ

(1)

其中，γc为边坡失稳破坏时的临界重度。

3 结果与讨论

3.1 粘聚力c对F的影响

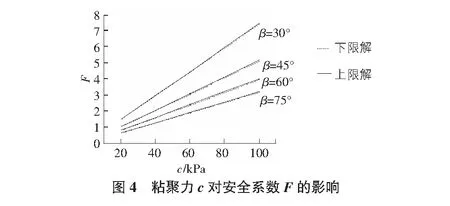
粘聚力c对安全系数F的影响如图4所示，土体的弹性模量取E=100 MPa，泊松比取ν=0.3，土体的重度γ=18 kN/m3，边坡高度H=10 m、内摩擦角φ=10°。由图4可知，上限解和下限解的误差非常小，安全系数F随着粘聚力c的增大而线性增大。该规律和文献[3]的结果是一致的。

3.2 内摩擦角φ对F的影响

内摩擦角φ对安全系数F的影响如图5所示，土体的弹性模量取E=100 MPa，泊松比取ν=0.3，土体的重度γ=18 kN/m3，边坡高度H=10 m、边坡角度β=45°。由图5可知，安全系数F随着内摩擦角φ的增大而非线性增大，且增长速度随φ的增大而增大。

3.3 边坡高度H对F的影响

边坡高度H对安全系数F的影响如图6所示，土体的弹性模量取E=100 MPa，泊松比取ν=0.3，土体的重度γ=18 kN/m3，内摩擦角φ=10°、粘聚力c=20 kPa。由图6可知，安全系数F随着边坡高度H的增大而非线性减小，且减小的速度随H的增大而不断减小。

3.4 边坡角度β对F的影响

边坡角度β对安全系数F的影响如图7所示，土体的弹性模量取E=100 MPa，泊松比取ν=0.3，土体的重度γ=18 kN/m3，内摩擦角φ=10°、粘聚力c=20 kPa。由图7可知，安全系数F随着边坡角度β的增大而非线性减小，且减小的速度随β的增大而不断减小。

4 工程应用

湖南省永吉高速公路通往永顺至吉首，为湖南省西北部区域重要的省级通道，是湖南省高速公路网规划“七纵九横”中第七纵重要组成部分。采用本文方法对其中一路段的边坡进行稳定性分析。工程概况如下：土坡高度H=16.4 m、坡角β=45°、土体粘聚力c=35 kPa、内摩擦角φ=23°，γ=18 kN/m3。

根据数值模拟计算结果得到该土坡稳定安全系数的上限解为2.4、下限解为2.3。从而可以判断该土坡处于稳定状态，而且该土坡稳定安全系数较高，不需要对其进行额外加固。通车以来，通过对土坡的监控，尚未出现边坡失稳破坏。此外，采用本文方法对路段边坡的稳定性分析，有利于土坡加固方案的初步设计，在本工程中取得了良好的效果。