页岩气藏水力压裂中应力-流压耦合效应及人工裂缝扩展规律
2018-12-11张建光李湘萍王传睿吕爱民孙致学
张建光, 李湘萍, 王传睿, 吕爱民, 孙致学
(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.天津大学环境科学与工程学院,天津 300072)
页岩气作为重要的非常规油气资源,其规模及可采储量极其可观。中国页岩气资源分布广泛,在南方古老海相龙马溪组和筇竹寺组等页岩储层中普遍存在地层超压现象,压力系数普遍大于1.3,局部地区可超过2.3[1]。水力压裂技术作为提高油气采收率的有效工程技术,在超压页岩气开发中已经被广泛应用。在超压页岩储层的勘探开发过程中研究人员发现,孔隙流体压力的增加和储层岩石原始应力场之间存在着耦合作用。地层原始应力场与流体压力的耦合规律的研究,有助于加深对水力压裂过程中超压页岩储层应力场演化及裂缝扩展的认识,对压裂改造有重要的研究价值。由于超压地层的原始应力-流压耦合和水力压裂开采过程涉及到岩石力学、渗流力学、计算力学等过程,复杂且难以直接观察,因此国内外学者采用不同的方法进行了数值模拟研究。Fu等[2]建立流体-构造力学显式耦合理论模型,对裂缝体油藏进行水力压裂模拟;Meyer等[3]基于离散裂缝网络模型开发了MShale软件;王杰等[4]基于离散块体单元模型进行了岩石破裂模拟;雷群等[5]从地层应力与压裂压力的关系角度研究了低孔低渗介质压裂缝网形成机制;曾青冬等[6]利用位移不连续方法(DDM)对多簇压裂缝网的扩展进行了影响因素分析;赵金洲等[7]也在研究中国页岩气压裂设计中指出,水力压裂在单一裂缝脆弱面上将产生使裂缝发生转向的诱导应力,并得出了任意压力分布情况下的诱导应力场计算模型;Taron等[8]利用有限差分软件FLAC3D,以节理张开度为切入点,研究了地热岩的THMC耦合性质。但是前人的工作多基于连续介质假设,建立在宏观力学性质连续基础上进行研究,从细观离散元角度进行研究较为少见。笔者基于离散元方法的孔隙超压和水力压裂数值模拟,开展页岩气藏水力压裂中应力-流压耦合效应及人工裂缝扩展规律研究。
1 初始应力场与流体压力耦合关系
页岩储层多具有近生烃源和一体生储成藏的特征。超压页岩储层经历了高度成熟演化和强烈地质构造运动,常见的增压机制包括构造抬升型、水热型、黏土矿物脱水型、生烃型[9]。根据Biot提出的修正有效应力原理,即将地层应力σ看作是关于流体压力pp的函数,用以解释当孔隙空间内充有流体并且存在压力时岩石介质的形变现象。基质颗粒受力状态由地层应力和孔隙流压共同控制,其表达式为

(1)

(2)
kij(σ,pp)=k0exp(βΔn).
(3)

由Biot理论可知,孔隙流体压力的增加会降低岩石介质所受的有效应力。在美国海湾滨海地区、文莱、委内瑞拉、加拿大以及北海地区等存在地层压力异常的油气田开发过程中,一系列压力监测的结果都证明,孔隙中的压力pp和最小主应力σh之间都存在耦合关系。Engelder等[10]基于英国North Sea Garben超压区块以及加拿大Scotian Shelf油砂次盆地开采过程中地应力及孔隙压力演变数据,假定地层垂向应力σv为最大主应力且最小主应力σh在水平方向上,提出了流体压力与岩石介质应力的耦合关系简化公式:
(4)
式中,σh为最小主应力,MPa;σv为最大主应力,MPa;ν为泊松比;a′为比奥系数。
可以看出,Engelder等[10]是在基于最大主应力与最小主应力相互垂直的前提下,假设垂向应力σv为最大主应力,研究了垂直剖面上流体压力与应力的耦合关系,而在实际地层中的水平平面上也存在相互垂直最大水平主应力和最小水平主应力。以此为基础,本文中对水平方向上应力-流压耦合作用及其对水力压裂裂缝扩展的影响进行探讨,开展基于离散元方法的孔隙增压和水力压裂细观数值模拟研究。
2 颗粒流数值模拟计算耦合原理
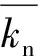
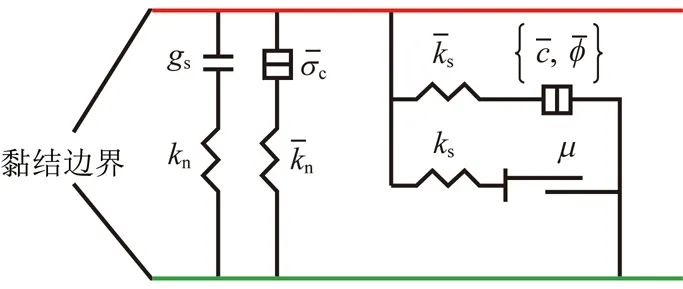
图1 平行黏结模型示意图Fig.1 Sketch of parallel bond model
基于平行黏结的胶结颗粒模型,通过岩体孔隙压力变化引起的裂缝扩展的模拟研究地层应力和流体压力之间的耦合作用,该耦合作用主要基于以下假设:
(1)岩体内的孔隙通道为管-域模型(pipe-domain model)。 流体的流动通道为颗粒接触位置的平行板通道,称之为“管道”,即为图2中的黑色线段所示;流体的存储单元为颗粒间的孔隙单元,称之为“坝颉北,如图2中红色线段围成的区间即为域的空间,黑色圆形部分为域的中心点,相邻的域之间通过管道相连。
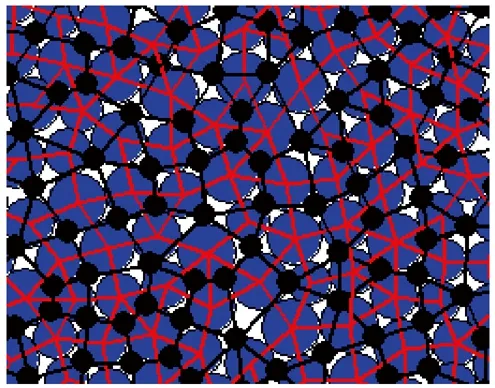
图2 管-域模型Fig.2 Model of pipes and domains
(2)页岩储层具有低孔低渗的特征,颗粒间孔隙的体积非常小,油气储层内流体的运动通道多为“孔隙-裂缝”,因此本模型对水力压裂过程中水体压缩的影响忽略不计。
模拟流体-应力耦合的管-域模型可以看作是由基质颗粒、胶结物、裂缝、原生孔隙组成的多孔胶结体。假设物质孔隙储水,裂缝管道导水,由裂隙介质的导水作用,在双重介质系统内形成两个水头,即孔隙介质中水头和裂缝介质中水头,两种介质之间通过水流交换项联系。由于裂缝和原生孔隙的孔隙度和渗透率差别很大,因此计算流体在二者间的运移时,通过立方定律建立细观裂缝与孔隙域之间的交换关系为
q=ka3(p2-p1)/L.
(5)
式中,k为传导系数;a为管道平均孔径,m;p2-p1为相邻域的压力差值,Pa;L为相邻接触颗粒半径之和,m。
根据颗粒黏结所受法向压力的情况分析,当法向压力为0时,管道的孔径等于残余开度孔径,随着法向压力的增大,裂缝开度减小。二者的关系可定义为
α=α0F0/(F+F0).
(6)
式中,α0为颗粒间接触力为0时的管道孔径,又称为残余开度孔径,m;F0为管道孔径α减小到0.5α0时的法向压力,Pa。相邻域通过与之相连的管道进行流体置换,在一个时间步长Δt内,域内的流体压力变化为

(7)
式中,Kf为流体的体积模数;∑q为该域从周围管道中获得的总流量体积,m3;ΔVd为孔隙域视体积的变化量,m3。
如图3(图3中s为相邻两颗粒间的间距,即流体压力运动的作用截面宽度,m)所示,域内的流体压力p会均匀作用在固相颗粒表面,因此颗粒受到的合力为

(8)
式中,β为流体域边界夹角的半角。
由上述分析可知,胶结颗粒模型与流体之间的耦合通过以下3点实现:①通过颗粒间接触力的变化来实现通道孔隙的变化,不同域内的流量交换增加;②通过作用在颗粒上的力改变域的空间结构,进一步改变其中的压力;③域内的孔隙压力对其周围的颗粒有推移作用。
图4为耦合循环计算原理流程。

图3 颗粒所受流体压力Fig.3 Fluid pressure acting on particle

图4 流压-应力耦合计算原理Fig.4 Calculation principle of flow pressure-stress coupling
3 孔隙增压及水力压裂模拟方案论证
3.1 数值模型建立及参数确定
查阅国内外页岩储层的相关力学参数,认为页岩储层弹性模量一般为530 GPa,泊松比为0.2~0.4,抗剪强度为10~70 MPa[12]。在数值模拟中为了使数值模型更加接近真实页岩物性,同时考虑到流体压力和应力耦合计算的精度,在建模过程中还需要对模型细观力学参数和流体计算参数进行标定。由于尺寸效应的存在,无法直接通过宏观参数确定细观力学参数,因此需要采用反演标定的方法,通过调参得到合理的细观力学参数。
为验证数值模型能够表现出页岩的宏观力学物性,笔者借鉴文献[13-14]中的龙马溪组露头页岩力学参数作为用以标定的宏观力学参数试验数据,进行未加孔隙流压情况下的单轴压缩模拟试验并记录岩样的应力-应变曲线。与前人所做的实验室条件下的物理试验数据进行比对,结果如图5所示。从图5中可以发现室内试验与数值模拟的峰值强度接近,且室内试验结果与数值模拟结果曲线具有非常好的趋势一致性,因此可认为建立的数值岩样模型的细观力学参数符合要求,可以进行相关数值试验。
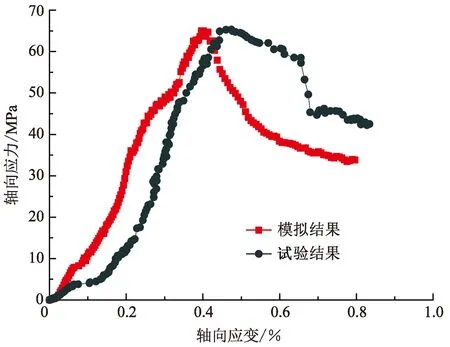
图5 室内试验与数值模拟的单轴压缩试验应力-应变曲线Fig.5 Stress-strain relationships observed in numerical and experimental uniaxial compression tests
经过反复试算,确定页岩细观力学参数如下:颗粒摩擦系数为0.557,颗粒接触模量为10.5 GPa,颗粒法向切向刚度比为2.5,接触黏结平均法向强度和切向刚度均为24 MPa。模拟中流体计算参数参考杨艳等[15]对孔隙流体计算参数的敏感性分析,对流体计算参数赋值如下:流体黏度μ为1.5 mPa·s,流体体积模数Kf为0.01 GPa,残余孔径α0为1.0 μm,初始法向压力F0为5.0×106N,时间步长设置为5×10-4s。
通过试错法反演出的页岩岩样模型的尺寸为2 m×2 m,孔隙度为0.07,共生成12 443个颗粒,最大最小颗粒粒径比为1.66,颗粒平均半径为9 mm,颗粒半径服从均匀分布。颗粒之间的黏结类型为平行黏结,黏结强度服从正态分布。岩样模型的宏观密度为2 532 kg/m3,弹性模量为14.06 GPa,泊松比为0.367,单轴抗压峰值强度为118.0 MPa,单轴抗拉强度11.67 MPa。数值模型如图6所示。

图6 建立的数值岩样模型Fig.6 Numerical rock specimen
3.2 试验方案设计
3.2.1 原始应力场与孔隙压力耦合方案设计
为探讨水平方向上孔隙增压与原始应力场之间耦合关系,计划进行如下试验方案。先通过伺服施加围压模拟应力场,固定最大、最小水平主应力,然后将流压作用范围设定为整个模型孔隙,对数值岩样模型进行整体孔隙增压,改变孔隙流体压力,分别设置10、10.5、11和11.5 MPa的孔隙流体压力为对照组,分析孔隙水压力增压对岩样模型的力学性质影响;固定y方向的最大水平主应力为40 MPa和孔隙压力不变,x方向最小主应力分别设置成32.5、35、37.5和40 MPa作为对照组,分析最小水平主应力对孔隙存在流压的岩样模型的力学性质影响。设计8组不同最小水平主应力和孔隙压力下数值岩样模型,分别对8组数值模型进行直剪试验(图7),用以分析孔隙流体压力及主应力对地层岩石介质的力学性质的影响,具体方案见表1。

图7 直剪试验Fig.7 Direct shear test
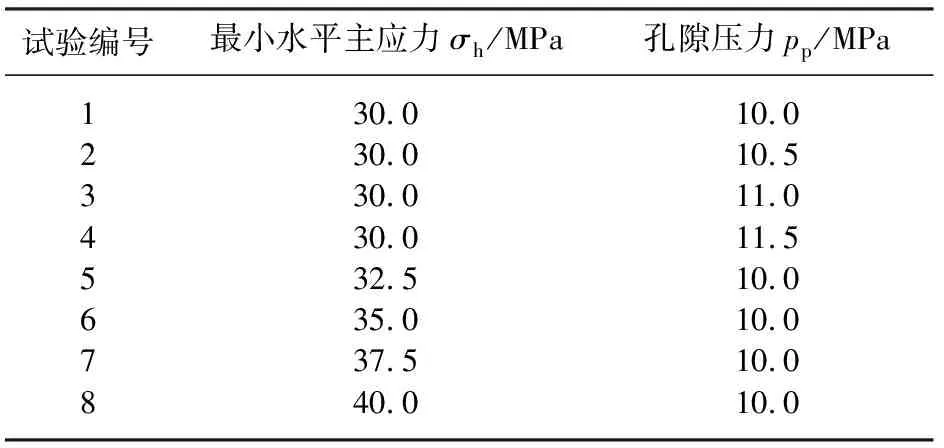
试验编号最小水平主应力σh/MPa孔隙压力pp/MPa1234567830.030.030.030.032.535.037.540.010.010.511.011.510.010.010.010.0
3.2.2 原始应力场与压裂流体压力耦合方案设计
为研究存在地层孔隙超压现象的原始应力场和水力压裂流体压力之间的耦合作用及裂缝扩展规律,针对水力压裂流体具有高能量、高压力、大排量的特点,分别从注入压力和地应力场分布对裂缝扩展影响的角度设计了水力压裂数值模拟试验,方案为:对岩样模型通过墙体围压加载模拟应力场,固定水平应力差异系数为20%,设定x、y方向的主应力为定值,改变注入流体压力,分别以70、75、80和85 MPa的注入压裂压力为对照组,向模型内部在模型中心设置半径为1.5 cm的圆形压力孔注入流体,分析不同流体压力对应力场的影响;保持y方向的最大水平主应力为40 MPa不变,设定x方向的最小水平主应力,分别以30、32.5、35和37.5 MPa的x方向应力为模拟对照组,在模型中心设置压力源并以定压力梯度向模型内部注入流体,分析不同水平应力差异系数下裂缝扩展规律。综上所述,本文中设计不同压裂压力和水平应力差异系数下的试验方案,见表2。

表2 不同压力和水平主应力比下的方案Table 2 Scheme for experiments under different fracturingpressuresand horizontal principal stressratios
4 模拟结果对比分析
4.1 原始应力场和孔隙增压耦合结果
结合岩样模型及流体计算参数,进行地应力条件下的岩样整体孔隙增压和直剪试验的细观数值模拟(图7),获得了页岩的应力-应变关系,图8为定最小水平主应力下不同孔隙压力岩样模型的应力-应变曲线。从图8可以看出,岩石应力-应变的前期的弹性变形阶段(A—B段),不同孔隙压力下的变化趋势大致相同,曲线斜率即弹性模量可近似看作等值;随着孔隙压力的增加,岩样模型的峰值强度变大且峰值应变右移,在4组模拟方案中,孔隙压力10、10.5、11和11.5 MPa对应的峰值强度分别为2.26、2.41、2.63和2.74 MPa,对应的峰值应变分别为0.62%、0.71%、0.77%和0.94%。由式(1)可知,地层岩石骨架受到的有效应力为原始地应力与孔隙流体压力的差值,局部岩样孔隙整体增压会抵消一部分原始地层应力,细观上反映为颗粒间胶结部分承受的法相接触力以及切向接触力下降(图1),削弱了颗粒间胶结物的初始承载,提高了其极限破坏强度;宏观上表现为地层岩石介质所受的有效应力降低,增强了岩石的塑性及抗剪切破坏能力。
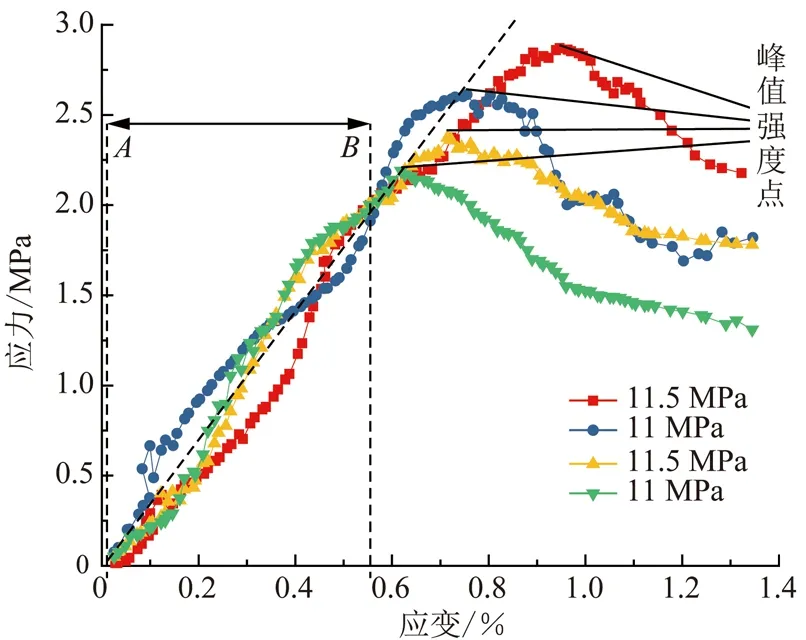
图8 不同孔隙压力下数值试样剪切应力-应变关系Fig.8 Relation of differential shear stress-strain of numerical specimens under different pore pressures
图9为不同最小主应力下的岩样模型直剪试验的应力-应变曲线。可以看出,随着最小水平主应力的增大,岩样模型的峰值强度逐渐增大;岩样模型的弹性变形初期阶段,应力与应变成正比例关系,曲线斜率随着最小水平主应力的增加而增大,在应力-应变曲线中斜率表征岩石的弹性模量,说明固相介质所承受的最小水平主应力与弹性模量呈正相关关系。这与文献[16]中的试验与分析结果相同。
根据上述模拟结果并结合格里菲斯-库伦破裂准则,对原始应力场与孔隙流体无差异增压之间的耦合关系进行分析。图10(a)为传统的格里菲斯-库伦破裂准则下的孔隙增压影响下应力路径,莫尔圆的直径为水平差异应力值。图10(b)为考虑应力场和孔隙流体增压耦合作用的修正格里菲斯-库伦破裂准则,基于公式(4)提出的最大主应力与最小主应力相互垂直的前提条件下,假设最大主应力为水平最大主应力且不发生改变,当发生岩样孔隙流体增压后,公式(4)中的系数项增大,水平应力差异系数减小,应力变化过程反映在应力路径图上的变化上如图10(b)所示,莫尔圆在左移的过程中直径逐渐减小,增大了与破裂包络线相切的难度。综上所述,初始应力场与孔隙增压存在耦合关系,孔压变化会引起水平差异应力变化,并对岩体的稳定性起到促进作用。
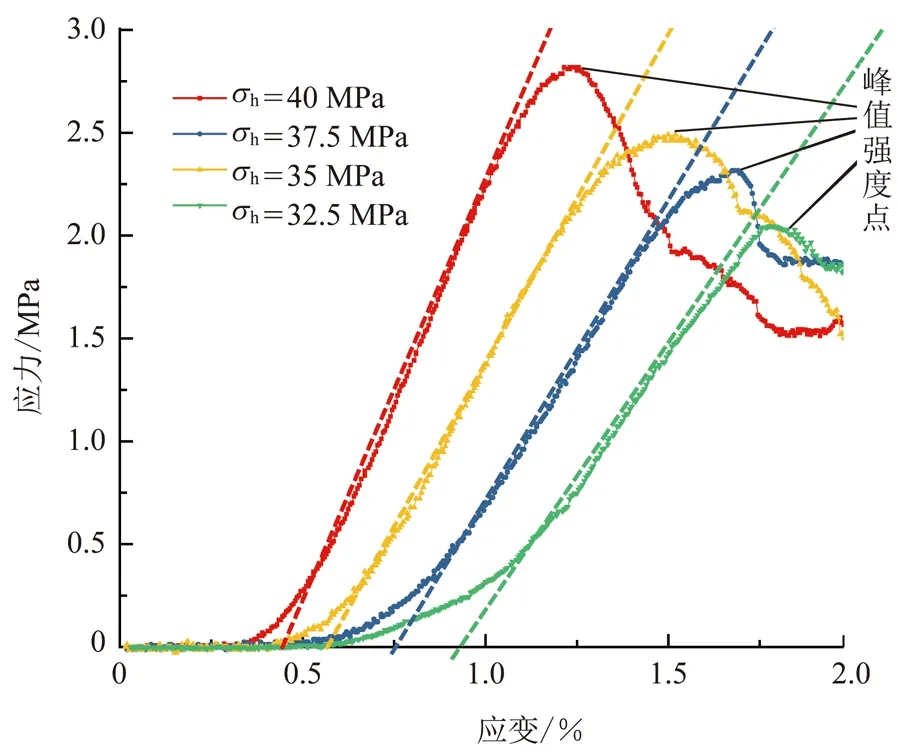
图9 不同最小水平主应力下数值试样应力-应变关系Fig.9 Relation of differential shear stress-strain of numerical specimens under different minimum horizontal principal stress
4.2 原始应力场和压裂流体压力耦合结果
4.2.1 应力场与压裂流体的耦合作用
设定压裂压力pf为80 MPa,在水平方向上假设地层初始最大水平主应力不发生改变,通过增加初始最小水平主应力的值改变水平差异应力,并对处于应力场中的数值试样进行水力压裂模拟,结果如图11所示。从图11能够看出,当水平差异应力Δσ为0(即水平应力差异系数为0)时,定压力下裂缝改造面积较小且无规律性,增大水平差异应力系数,裂缝改造面积增大并呈现出明显的方向性。此外,从图11中还可以观察到随着Δσ的增加,微裂缝扩展方向从由压裂中心点向周向均匀扩展逐渐转为平行于最大水平主应力方向。这是因为随着压裂作业的进行,压裂液通过破坏岩石介质进入其孔隙中,造成局部孔隙具有极高的压力并形成新裂缝。根据断裂力学理论,裂缝尖端具有应力奇异性,而裂缝尖端处的应力集中使该处的岩石破坏强度小于其他区域,故而流体压力在裂缝尖端位置更易进行聚集和运移。
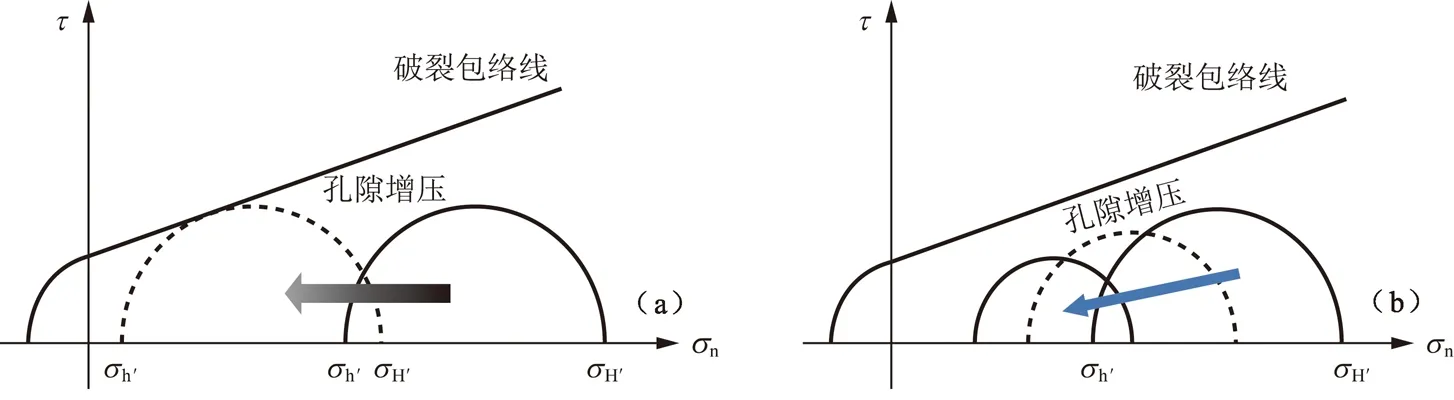
图10 孔隙流体超压对岩石破裂影响Fig.10 Influence of overpressure pore fluid on rock failure

图11 定80 MPa压裂压力下不同水平差异应力裂缝最终扩展形态Fig.11 Final fracture-morphology under different horizontal principal stress ratios, 80 MPa fracturing pressure
在压裂过程中考虑应力-流压的耦合效应,与传统观念(图12中实线黑色莫尔圆)相比,地层水平差异应力系数的降低会引起孔隙形状及流体受力状态的改变,使压裂破坏过程的应力路径中莫尔圆左移并变小,增大了莫尔圆与破裂包络线相切难度(图12中虚线蓝色莫尔圆),增强了岩石的抗破裂能力。简言之,水平差异应力系数与水力压裂作业效果有密切联系,水平差异应力系数越小,人工裂缝改造面积越小,压裂作业效果越差。
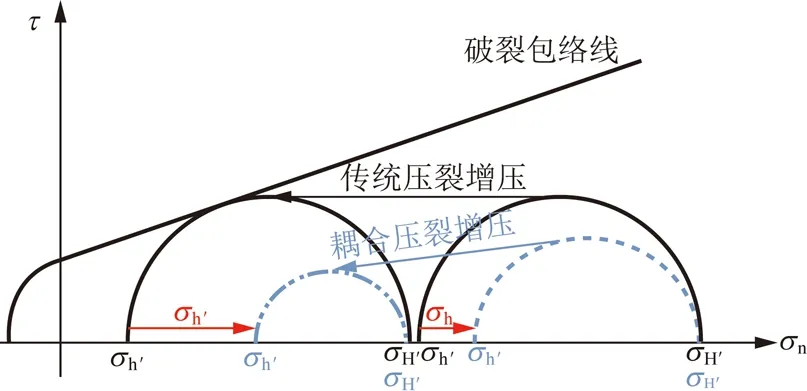
图12 水力压裂对水平方向岩石破裂影响Fig.12 Influence of hydraulic fracturing on rock failure
随着裂缝的发育,储层初始应力场会进行重构。图13为压裂后最小水平主应力分布云图。由图13可知,不同初始水平差异应力条件下压裂流体造成的局部超压区域形态各不相同,但应力场的变化呈相似性:水平差异应力的增加,使在垂直于裂缝扩展方向上的最小主应力增强,裂缝延伸尖端出现应力弱化,在岩样模型内部形成比较明显的应力强区和弱区。

图13 不同水平差异应力下水力压裂后最小水平主应力分布云图Fig.13 The minimum horizontal principal stress distribution nephogram of specimen under different horizontal differential stress
4.2.2 应力-流压耦合作用下裂缝扩展规律
图14为不同压裂压力下各时步裂缝扩展形态。从图14中可以看出,在存在孔隙增压及地层应力条件下,压裂作业并未形成单一主裂缝而是以微裂纹的形式发育,随着压裂压力pf增大,裂缝密度逐渐增加。微裂纹在y方向高度发育并扩展,x方向的裂纹发育被抑制。人工水力裂缝产状沿着最大应力方向扩展,与Erdogan等提出的最大周向应力理论相符。

图14 不同注入流体压力下各时步裂缝扩展形态Fig.14 Each time step of fracture-morphology under different inject fluid pressure
为研究压裂流体压力对裂缝扩展的影响,图15记录了不同压裂压力作业过程中裂缝数量的发育情况。从图15中可以看出,水力压裂裂缝扩展速率呈现先增大后减小(图中各曲线斜率变化)的趋势。低压裂压力pf时,微裂纹扩展速率增涨幅度较为缓和,后续裂纹发展速率相对均匀稳定;随着pf的增加,裂缝发育起点逐渐左移,pf越大微裂纹扩展速率提升程度越剧烈,待主要破坏完成后逐渐放缓。通过该现象,可以认识到注入流体压力会在页岩内部形成由微裂缝组成的复杂缝网,裂缝数量会在短时间内发展到一定峰值,继而裂缝生成速率逐渐减缓;提高pf能加快裂缝形成速度,更有助于裂缝的发育延展。
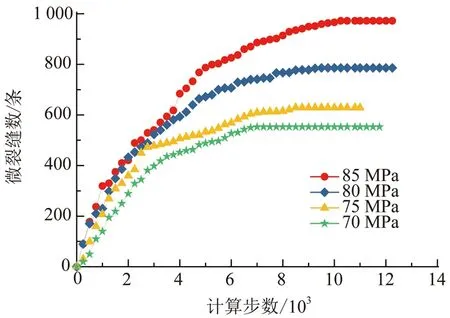
图15 不同压裂压力下裂缝扩展趋势曲线Fig.15 Curves of fractures development under different fracturing pressures
5 结 论
(1)水平应力场与孔隙流体之间存在耦合作用,水平差异应力随着固相介质内部孔隙流体压力的增加而减小,假设地层最大水平主应力不变,则最小水平主应力与固相介质的弹性模量及抗剪强度均为正相关关系,存在孔隙超压现象的岩石的刚度和剪切破坏峰值强度均有所提高。
(2)水平应力场与压裂流体之间存在耦合作用,流体压力一定时,地层水平差异应力越大,裂缝改造面积越大;应力-流压耦合作用下,流体生成的裂缝能够改变岩石介质所受最小水平主应力的大小及分布,最小水平主应力在裂缝尖端处弱化并朝着与裂缝垂直的方向偏转。
(3)裂缝发育速率及扩展范围均随注入流体压力增加而增加,加载速率呈现出迅速上升后放缓的趋势;水平最小主应力的大小及方向直接影响人工裂缝扩展方式,在水平方向上朝着最大周向应力方向延伸,最小周向应力方向的裂缝发育被抑制,随着水平差异应力的增加,这种趋势愈发明显。
