基于局部频率约束的动态快速匹配追踪方法

印兴耀, 许 璐, 宗兆云, 李 坤

(1.中国石油大学(华东)地球科学与技术学院,山东青岛 266580; 2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071)

匹配追踪算法可自适应地将信号在过完备原子库中分解为最佳匹配时频原子的线性组合。Mallat等[1]于1993年首次提出了基于Gabor型时频原子库的匹配追踪算法(Matching Pursuit),Chakraborty和Okaya[2]于1995年最早将匹配追踪算法应用于地震信号的分析中。与短时傅里叶变换[3]、连续小波变换[4]和S变换[5]等常规时频分析方法相比,匹配追踪算法的时频分辨率相对较高,是一种高精度的地震信号分解与重构算法。但传统的匹配追踪算法计算速度非常慢,不适用于大型数据的处理过程。针对匹配追踪算法的计算量庞大和运算效率极低的问题, 国内外专家学者提出了许多改进算法。Liu等[6-7]对Mallat的匹配追踪算法作了改进,率先提出了动态匹配追踪算法。张繁昌等[8]提出双参数动态子波库匹配追踪快速算法,既减少扫描参数的个数,又采用多原子分解策略,提高了匹配分解的效率。刘汉卿等[9]针对瞬时频率存在负值的情况提出了利用连续相位求取瞬时频率,基本解决了由主值相位和解缠相位求导获得的瞬时频率存在负值这一问题,但该方法也存在一定的问题,利用连续相位直接求取的瞬时频率容易受到噪声影响产生波动,出现一些频率异常值。地震属性大都是瞬时属性[10],像瞬时频率、瞬时振幅、瞬时倾角等,这些描述地震频率特征的属性依附于每个信号点的瞬时值。瞬时频率属性受相移、噪声及其他因素的影响,其可解释性差,很难反映微小的地质变化特征。局部属性描述地震特征并不依赖每一个数据点的瞬时值,而是参考这个数据点的局部邻近值,采用最小二乘估计策略,引进整形正则化对数据进行平滑处理,保证了局部频率的稳定性和可靠性。局部频率在各个领域都得到广泛的应用,陈常乐[11]应用局部属性进行火山岩识别技术的研究,陈双全等[12]应用局部频率属性检测天然气藏。基于以上研究背景,笔者针对匹配追踪的瞬时频率存在负异常的情况进行深入的研究,引入局部频率计算模式[13-14],将局部频率作为约束动态子波库的频率搜索参数。

1 基于局部频率约束的动态快速匹配追踪方法

1.1 动态快速匹配追踪算法

匹配追踪算法是一种基于子波库扫描的地震信号分解方法。假定被表示的信号为f,过完备原子库为D,H表示Hilbert空间,D由一组向量{gγ1,gγ2,…,gγk}构成,其中每个向量可以称为原子(atom),其长度与被表示信号f的长度相同,并且对这些向量已进行归一化处理,即‖gγ‖=1。

令信号f∈H,第1次迭代分解从冗余原子库D中选取一个与信号f最佳匹配的原子,即满足下式:

〈f,gγ1〉=supi∈(1,2,…,k)〈f,gγi〉.

(1)

式中,i为字典矩阵D的列索引;gγ1为第1次迭代搜索得到的最佳匹配原子;〈f,gyi〉代表信号与最佳匹配子波的內积运算;sup为〈f,gγi〉的上确界。

这样,经过一次迭代,信号f就被分解为在最佳匹配原子gγ1的垂直投影分量和信号残差两部分,即

f=〈f,gγ1〉gγ1+R1f.

(2)

式中,R1f为第一次迭代后得到的残差信号。匹配追踪算法是一个不断迭代过程[15],将残差信号R1f继续投影到原子库中,找到一个最佳匹配的原子,如此迭代下去。第n+1次迭代分解过程可以用下式表示:

Rnf=〈Rnf,gγn+1〉gγn+1+Rn+1f.

(3)

式中,Rnf和Rn+1f分别为第n次和第n+1次迭代完成后得到的残差信号;gγn+1为第n+1次迭代搜索得到的最佳匹配原子,其中gγn+1满足下式:

〈Rnf,gγn+1〉=supi∈(1,2,…,k)〈Rnf,gγi〉.

(4)

不断进行上述的迭代过程,直到匹配次数达到预设的迭代次数或信号残差能量小于能量阈值,则迭代停止。经过m步分解后,信号f被分解为m个最佳匹配的时频原子之和:

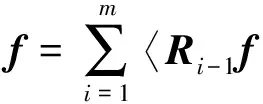
(5)

其中

R0f=f.

尽管传统的匹配追踪算法能够较好地表示信号,但因迭代分解的每一步都要将信号残差与冗余原子库中每一个原子进行内积运算,导致计算量过于庞大。因此专家学者们致力于在不损害匹配追踪算法的高分辨率的前提下,减少算法的计算量,使得算法的实际应用范围更广泛。Liu等[6]提出动态匹配追踪算法,利用复地震道分析技术得到信号的主频、中心时间和相位等先验信息,只需要确定这3个控制参数即可快速创建原子库以及实现对最优时频原子的扫描,由于每次迭代的时频原子的搜索范围会随着最大包络振幅位置发生变化,因此称该搜索策略为动态最优搜索方式,这使得贪婪的匹配追踪算法运算效率得到显著提高。

在对信号进行匹配分解过程中,每次迭代只在信号包络振幅最大值处进行,这样的分解策略使得每次迭代历经搜索范围内所有的原子,仅得到一个最佳匹配的时频原子,影响了信号的收敛速度。张繁昌等[8]提出了双参数动态子波库匹配追踪快速算法,不仅减少匹配子波的控制参数,且采用多原子分解的策略,即每次迭代并不是只在包络振幅最大值处进行匹配搜索,而是在满足一定条件的极大值位置处都进行搜索,这样一次迭代就能得到若干个匹配子波。各匹配子波的振幅可以通过阻尼最小平方的方法来确定,大大提高了分解的效率。

在迭代分解前,动态快速匹配追踪算法首先考虑原始信号中所包含的瞬时频率、瞬时相位、时间等先验信息,进一步约束其搜索半径,因此每一次的搜索方式可以简单表述为

gγi={u0,ω∈U[ω(u0),δω],φ∈U[φ(u0),δφ]},i=1,2,…,M.

(6)

式中,M为每次迭代得到的最优时频原子的个数;u0为时间中心,ω和φ表示地震信号瞬时频率及瞬时相位的先验信息[16];U[ω(u0),δω]、U[φ(u0),δφ]为频率和相位的搜索邻域;δω、δφ为相应参数搜索半径。

经过k次迭代后,得到信号残差Rkf,在第k+1次迭代中,假设共得到M个最优时频原子gγi(i=1,2,…,M),则第k次迭代得到残差信号Rkf可以表示为

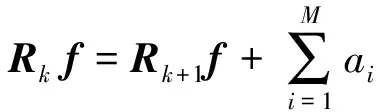
(7)

式中,ai(i=1,2,…,M)为第k+1次迭代得到的各时频原子的振幅。

1.2 局部频率约束方法

Taner等[17]提出复地震道分析技术,首次将瞬时频率引入到地震领域,之后瞬时频率成为一种重要的地震属性。后来许多学者提出瞬时频率的近似算法,Barnes等[18]提出了3种瞬时频率的近似计算方法;高静怀等[19]提出小波变换域瞬时频率分析方法;尹继尧等[20]提出基于TK能量的最大峰值瞬时频率计算方法等。

考虑到传统瞬时频率的不稳定性,本文中提出用局部频率替代瞬时频率并应用于动态快速匹配追踪算法中。局部频率算法不仅能处理噪声强的数据,即使是部分缺失的数据也能高效准确地处理。局部频率算法应用的是整形理论(也称数据规则化),整形理论是一种通过对矩阵进行操作包括逆矩阵计算的数据平滑算法。对于地震数据部分微弱或缺失的情况,局部频率算法可以从邻近的时间窗口内提取有效信息进行处理并得到合理的频率结果。

假设x(t)代表地震道,是时间t的函数,则相应复数道表示为

c(t)=x(t)+ih(t).

(8)

其中h(t)为x(t)的希尔伯特变换,也可以用振幅A(t)和瞬时相位φ(t)来表示复数道,如下式:

c(t)=A(t)eiφ(t).

(9)

其中

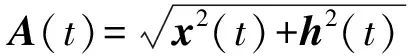
φ(t)=arctan[h(t)x-1(t)].

式中，A(t)为地震道的包络振幅;φ(t)为瞬时相位。

瞬时频率是瞬时相位的导数,也就是瞬时相位的变化率,因此地震道的瞬时频率属性ω(t)的数学表达式为

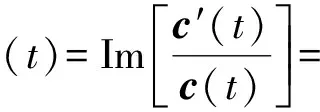
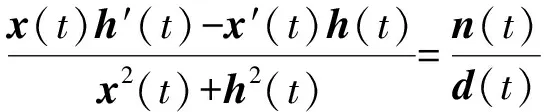
(10)

将瞬时频率的数学表达式写成向量表达式的形式,把时间记录看成是一个向量,通过定义一个对角矩阵和两个向量,即

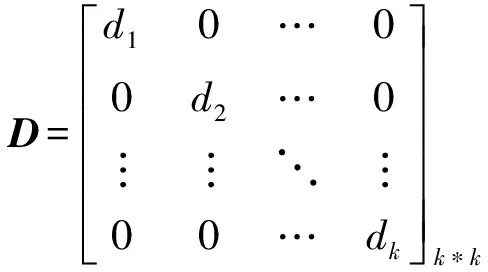
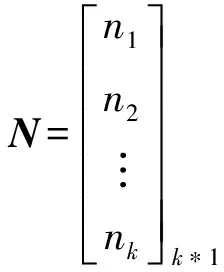
(11)

式中,k为地震道的采样点数。利用式(11)将方程(10)写成矩阵形式,即

W=D-1N.

(12)

式中,W为瞬时频率向量ω(t);N为由式(10)中的分子n(t)构成的向量;D为由(10)式中的分母d(t)构成的对角矩阵算子。注意到,矩阵D中很多元素很小甚至是零,为了避免式(12)出现“除以零”导致计算错误的现象,在分母上加一阻尼项ε,因此方程(12)变为

Winst=(D+εI)-1N.

(13)

式中,I为单位运算符。这里阻尼项ε并不能让瞬时频率变得稳定,但可以减弱瞬时频率受噪音和不稳定性因素的影响。

局部频率属性将式(13)作为线性反演的正则化形式,用一个一般化的正则化算子R代替单位矩阵I来改变正则化形式,因此局部频率的定义如下:

Wloc=(D+εR)-1N.

(14)

式中,R为正则化算子,以确保局部频率的连续性和光滑性,使得计算结果具有更高的信噪比。也可以选取整形正则算子S[21],对式(14)做进一步的约束,求解得到下式:

Wloc=(λ2I+S(D-λ2I))-1SN.

(15)

式中,λ为尺度因子,通常选自矩阵D的最小二乘范数。利用迭代反演方法求解时,通过λ进行缩放,可以保留原始物理维度,并能够加快收敛速度。

为了验证局部频率的可靠性,设计了3个用于比较信号频率属性的测试信号。图1(a)为一个频率由10 Hz增大到60 Hz的线性调谐信号,图1(b)为由频率10 Hz的Morlet子波合成的理论信号,图1(c)为一道实际地震信号。图1(d)、(e)、(f)展示了依次对应于测试信号的瞬时频率,由于瞬时相位的突变不可避免地出现负异常现象,不能直接用于确定动态匹配追踪控制参数的搜索范围,图1(g)、(h)、(i)展示了3个测试信号的局部频率,可以明显看到局部频率的结果比较精确地贴近于真实值,克服了瞬时频率出现负值的问题。

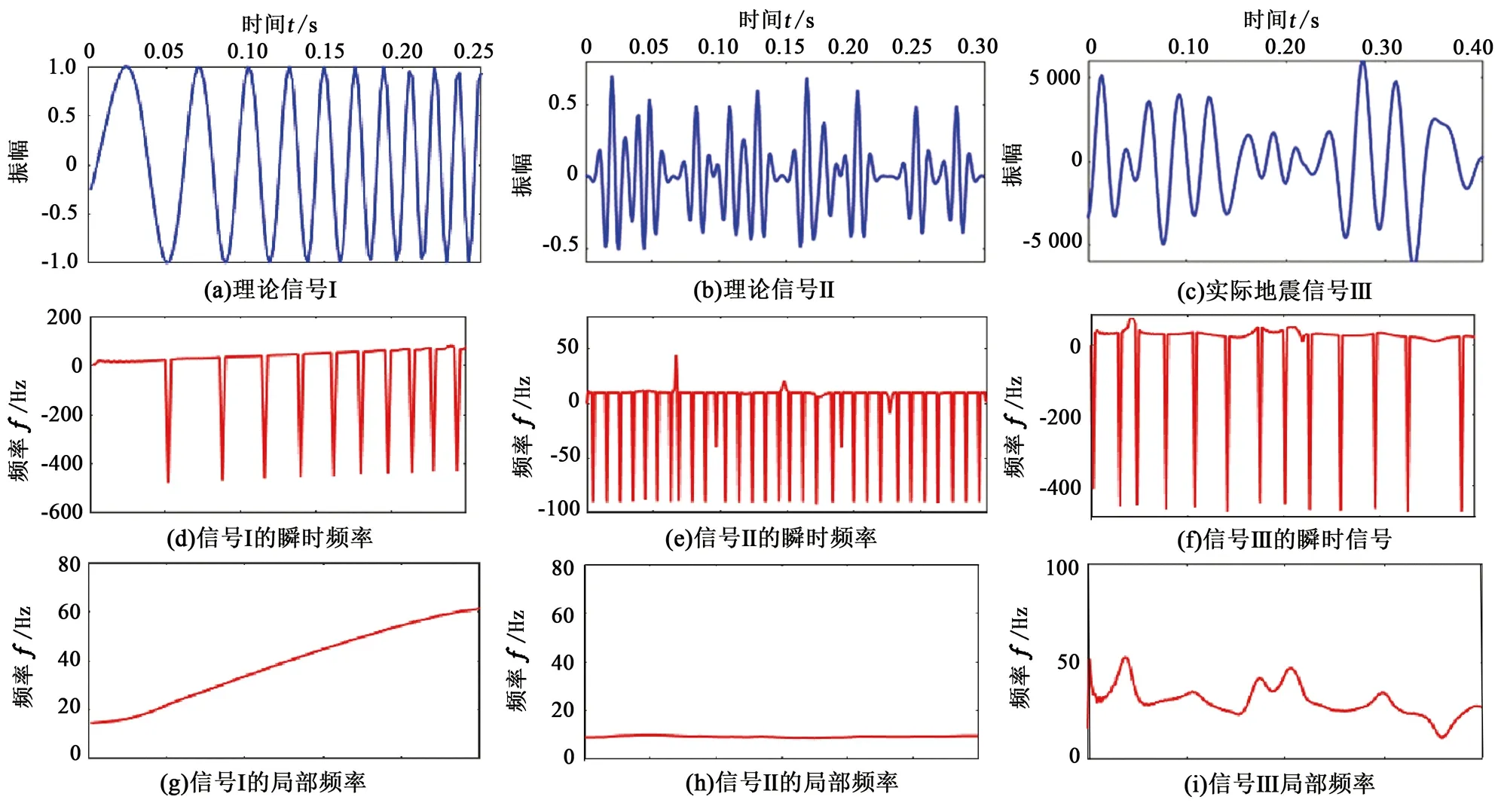
图1 不同信号的瞬时频率和局部频率对比Fig.1 Comparison of instantaneous frequency and local frequency of different signals

验证局部频率的抗噪性。同样采用图2中的两个理论信号,加入10%的噪声,如图2(a)和(d)所示。从两个理论信号的瞬时频率图2(b)和(e)可以看出瞬时频率受噪声影响波动大,极不稳定,而局部频率图2(c)和(f)的结果与理论值相符,基本不受噪声的影响,比较稳定。

对比以上的瞬时频率与局部频率的运算结果可以明显地看出,局部频率的结果比较精确地贴近于真实值。将局部频率引入动态快速匹配追踪方法中,用局部频率替代传统的以信号的瞬时频率作为动态参数的扫描范围。不仅避免了常规方法的负频率异常现象,并且抗噪性也得到改善,计算结果稳定。图3为基于局部频率的动态快速匹配追踪算法的流程。

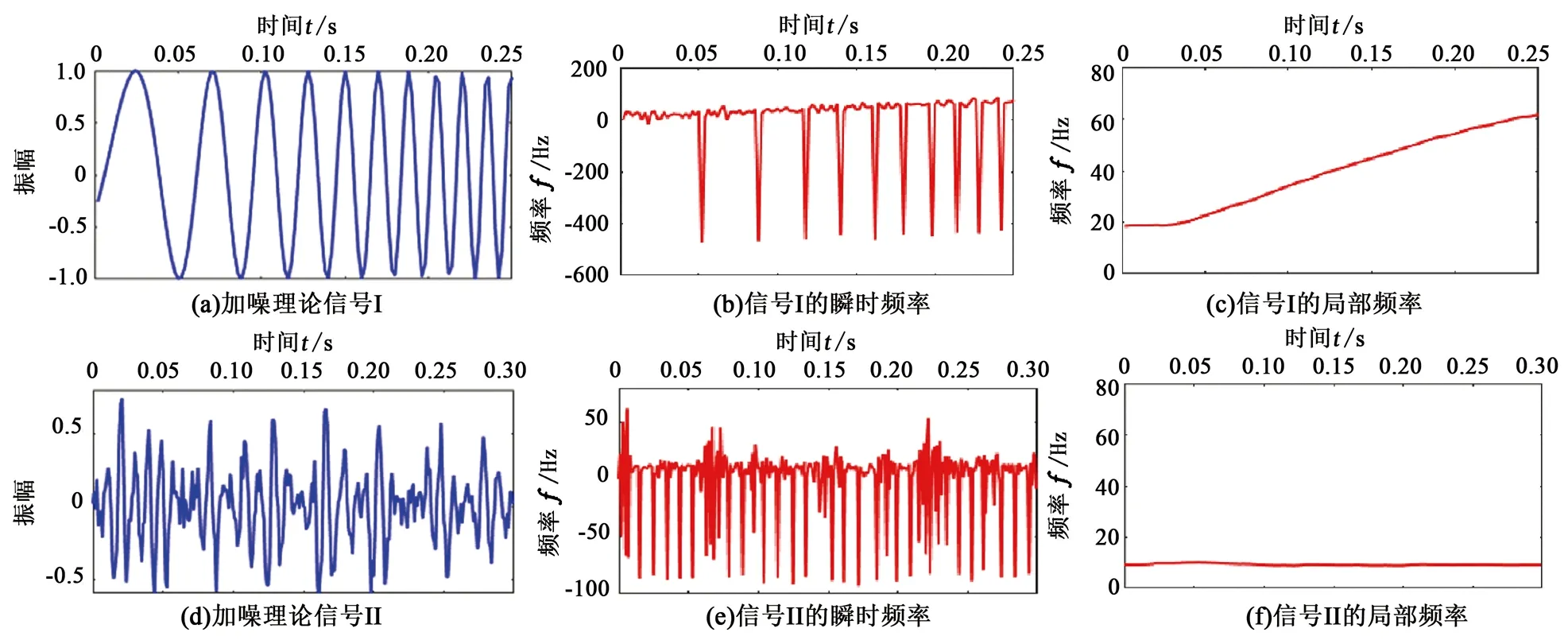
图2 加入10%噪声的理论信号的瞬时频率和局部频率对比Fig.2 Comparison of instantaneous frequency and local frequency of different signals with 10% noise

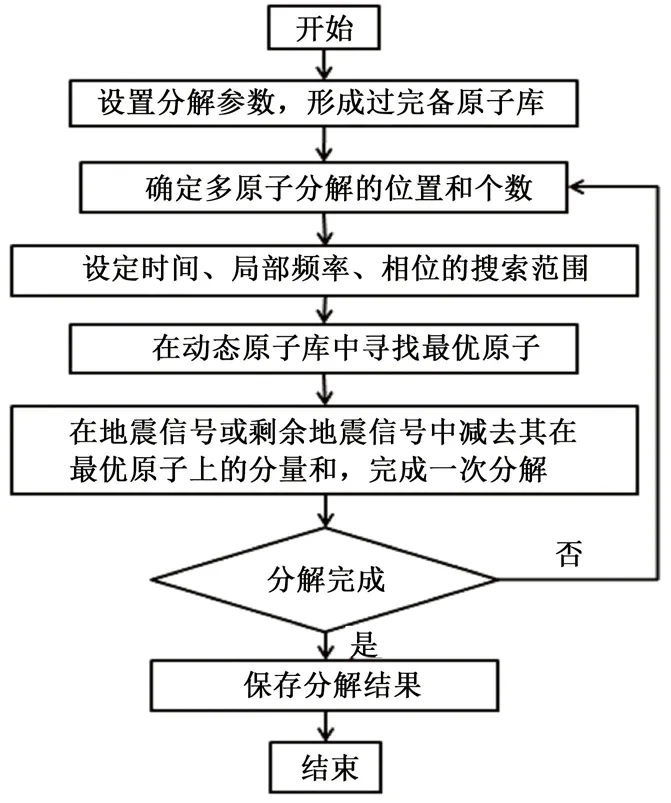
图3 基于局部频率约束的动态快速匹配追踪方法流程Fig.3 Flowchart of dynamic and fast matching pursuit method based on local frequency constrains

2 理论信号测试

2.1 一维理论验证

为了验证基于局部频率约束的动态快速匹配追踪方法的可行性和稳定性,本文中分别设计了一维和二维地震模型进行验证。首先用11个不同频率、相位和振幅的Morelet子波合成一道理论信号,构建一维地震模型,对其用基于局部频率约束的动态快速匹配追踪方法进行分解,迭代分解结果如图4所示。可以看出理论信号可以完全由匹配子波重构得到,残差曲线为零值,对其增加5%的噪声,得到如图5的地震模型。从分解结果可以看出,在加噪声的情况下依旧能够得到与无噪声情况一致的匹配分解结果,迭代分解结果比较稳定。

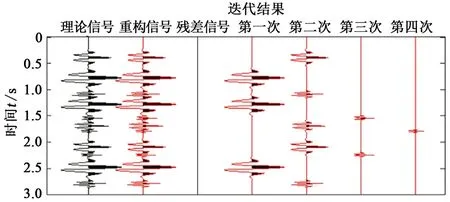
图4 一维合成信号的迭代分解结果Fig.4 Iterative decomposition results of one-dimensional synthesized signal

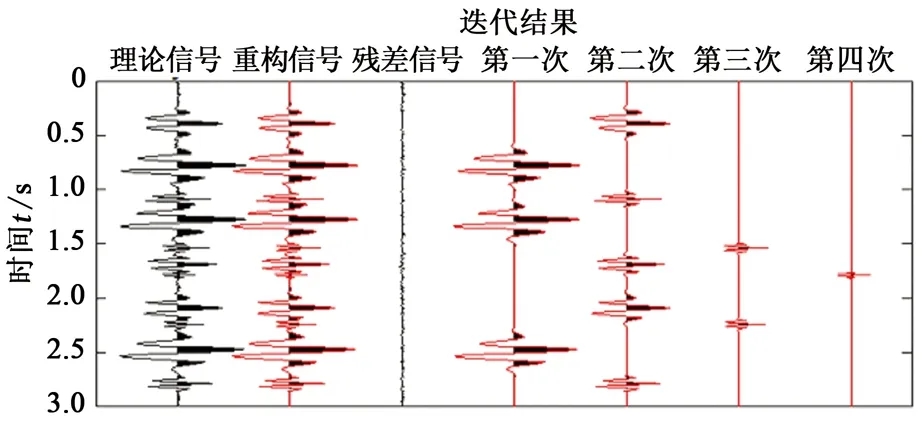
图5 加5%噪声的一维合成信号的迭代分解结果Fig.5 Iterative decomposition results of one-dimensional synthesized signal with 5% noise

2.2 二维理论验证

为了进一步验证基于局部频率约束的动态快速匹配追踪方法的可靠性,建立了如图6(a)的一个二维纵波阻抗模型。模型的复杂性有助于验证本方法基于局部频率的准确性。图6(b)为利用28 Hz零相位雷克子波合成的地震数据,对其用基于局部频率约束的快速匹配追踪方法进行匹配分解,图6(c)为重构的地震记录,并得到残差剖面(图6(d))。对图6(b)合成地震记录加入10%的噪声得到图7所示的结果。

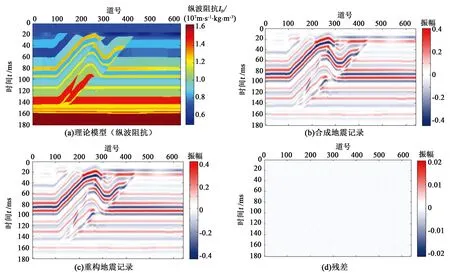
图6 无噪声的合成信号迭代分解结果Fig.6 Iterative decomposition results of synthesized signal without noise

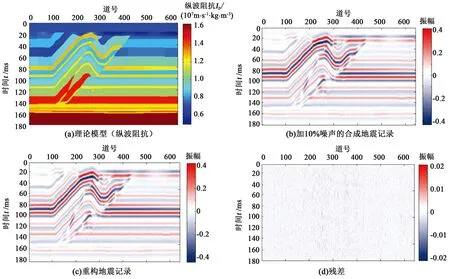
图7 加入10%噪声的合成信号迭代分解结果Fig.7 Iterative decomposition results of synthesized signal with 10% noise

从图6的迭代分解结果可以看出,基于局部频率的动态快速匹配追踪算法能够很好地对理论数据进行迭代分解,重构的地震剖面与原始地震剖面一致,残差基本为零。对地震记录加噪声后(图7),残差剖面所示基本为噪声信号，不含有效的反射信息，证明该算法具有一定的抗噪性。

3 实际资料处理

实际资料来自中国东部某勘探研究区,图8为某一实际地震剖面,为便于了解砂体的尖灭特征,将砂体的形态特征展布在地震剖面上,红色的椭圆框为砂体真正尖灭点位置,图9为用基于局部频率的MP时频谱分析的尖灭点识别结果。检测结果与实际尖灭点位置一致,很好地验证了本文中提出的改进匹配追踪快速算法在砂体尖灭线识别方法方面的可行性。

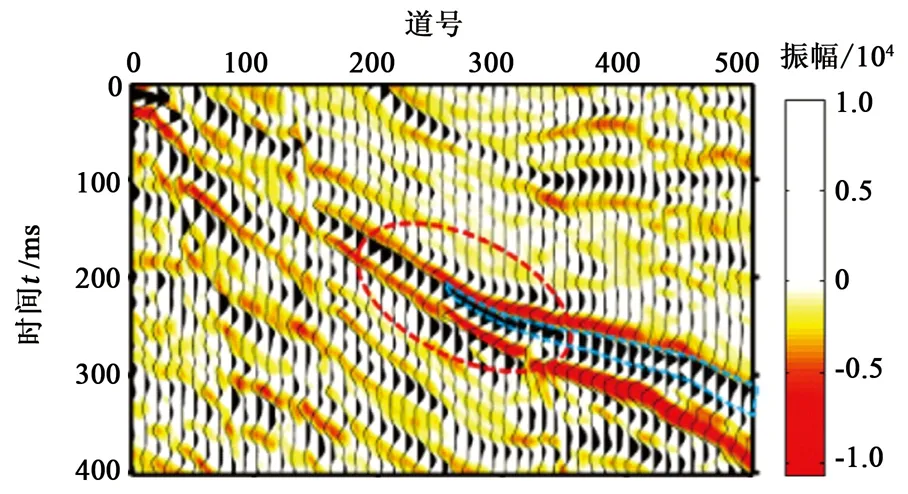
图8 实际地震剖面Fig.8 Real seismic profile

图9 尖灭点识别结果Fig.9 Tip point recognition result

为了对比本文中提出的改进的动态快速匹配追踪算法与传统的三参数动态快速匹配追踪算法,使用相同的迭代终止条件,对图8所在研究区的一道地震记录进行匹配追踪分解,从图10中可以清楚地看到,本文中提出的基于局部频率约束的动态快速匹配追踪算法提高了匹配分解的计算速度。

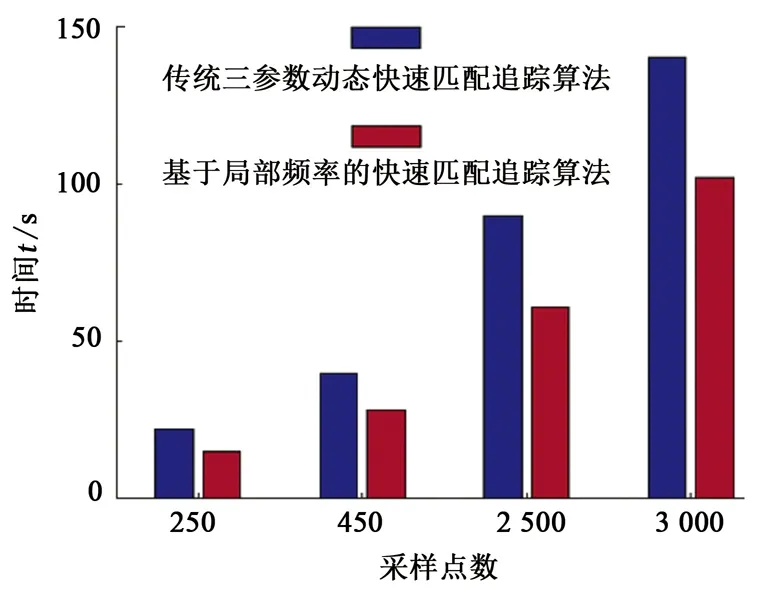
图10 两种匹配追踪算法计算时间对比Fig.10 Comparison of computing time of two methods

4 结束语

针对瞬时频率存在负异常现象且不稳定的问题,本文中发展了基于局部频率约束的动态快速匹配追踪算法,局部频率引进整形光滑算子,其计算过程并不是依附于每一个数据点的瞬时值,而是参考这个数据点的局部邻近值求取的,因此即使是在部分信号微弱或缺失的情况下,局部频率也能从邻近的时窗内提取有效信息并得到合理的频率值。相比于瞬时频率由于瞬时相位求导存在负频率现象,且受噪声影响大,计算结果极不稳定,本文中通过设计理论信号与实际信号验证了局部频率的可行性,其抗噪性得到增强,计算结果稳定,可以直接将其应用于匹配追踪的运算过程。在确定动态快速匹配追踪先验信息的搜索范围时,以局部频率替换瞬时频率,加快了运算效率。最后将基于局部频率约束的动态快速匹配追踪方法用于识别砂体尖灭点,在单频瞬时谱剖面上可以清楚看到砂体尖灭位置,且与实际位置一致,且运算速率明显提高,从而验证了本文中提出的改进匹配追踪算法的可行性。