大型环枝状油田注水管网系统运行优化
2018-12-11梁永图周星远张浩然王博弘孟令尊
梁永图, 周星远, 邱 睿, 张浩然, 王博弘, 孟令尊
(1.中国石油大学(北京)城市油气输配技术北京重点实验室,北京 102249; 2.大庆油田有限责任公司第六采油厂,黑龙江大庆 163511)
注水是保持油层压力、实现油田高产稳产和改善油田开发效果的重要途径[1-2]。地面注水管网系统主要运行工艺为:注水站通过高压注水泵将水注入到注水管网干线中,干线再将水分配到支线上的各个配水间,配水间根据所管辖各注水井需求注水量分配流量,最终将水送往终端注水井[3]。目前中国大多数油田注水管网系统为多源系统,即整个管网包含多个注水泵站[4],其中部分为大型复杂结构的环枝状注水管网,由于各注水泵站之间以及管网中各管段之间的相互影响,整个管网系统水力工况十分复杂。在管网实际运行过程中,运行方案主要依靠人工经验反复尝试制定,致使工作效率低下,且造成管网运行能耗较高,注水效率较低。国内学者大多针对此问题建立非线性数学模型,采用人工智能算法或者启发式方法求解。刘扬、曾文等[5-6]考虑注水管网运行参数约束,以注水能耗最低为目标建立模型,并采用模拟退火遗传算法求解;关晓晶等[7]采用混合遗传算法,崔智敏等[8]采用改进遗传算法、魏立新等[9]采用惩罚函数法结合遗传算法对油田注水系统运行优化模型进行求解;任永良、张瑞杰等[10-11]分别基于约束变尺度法和二层递阶迭代策略提出了启发式求解方法,将注水管网模型中流量、压力约束分为两阶段求解。国外学者针对城市配水、给水排水管网优化问题的研究相对较为深入,一定程度上对油田注水管网系统运行优化研究具有借鉴意义。Lan等[12]针对供水管网系统建立了非凸、非线性数学模型并采用一种分支剪枝全局优化算法(branch-and-reduce algorithm)进行求解;Bonvin等[13]利用启发式搜索方法对枝状配水管网泵站进行优化调度,动力费用降低约10%;Costa等[14]针对配水管网系统建立MILP模型,并采用分支定界法求解;Habibi等[15]利用多目标粒子群优化算法求解出最经济的管网泵站运行方案。油田注水管网优化模型通常规模较大、变量较多且耦合关系复杂,涉及非线性规划[16]、组合优化[17-18]等多个子问题。国内学者针对此问题建立运行优化数学模型,适用管网结构简单,考虑约束条件较少,模型实用性一般。国外学者虽然在模型建立与求解方面研究较深入,但研究对象大多为城市配水管网或大型泵站,针对油田注水系统运行优化的研究较少[19-20]。笔者针对大型复杂结构的环枝状油田注水管网系统,将注水站、注水井现场工艺约束以及管网运行流量、压力约束等约束条件考虑在内,以注水系统运行能耗与注水井注入偏差量损失之和最小为目标建立MINLP模型。提出一种蚁群算法结合线性近似与单纯形法混合分段求解的求解策略,采用蚁群算法优化求解离散变量,线性近似方法处理模型中非线性约束,最后采用单纯形法求解LP模型。
1 模型建立
根据油田现场注水工艺,整个注水系统运行方案在其管辖每口注水井需求注水量确定后较长时间范围内保持不变,模型中实际注水量以及注水站开泵方案等关键决策变量与时间变量无关,因此本文在建立数学模型过程中未考虑时间变量对管网注水方案的影响。一旦某些注水井需求注水量或管网其他已知条件发生变化,将更新的已知参数代入数学模型并进行求解,即可得出变化后满足现场工艺要求的最优运行方案。模型中采用现场实际应用的吸水指数方程处理注水井注入压力与流量的关系[21],即注入压力随注水量变化的线性方程,其中吸水指数指单位注水压差下的日注水量;并采用目前广泛应用于给水排水及油田注水系统的海曾威廉公式计算各管段流动沿程摩阻损失,海曾威廉公式适用于计算较光滑圆管满流水管道的沿程摩阻损失,粗糙系数以及沿程摩阻系数更方便得到,适用于工程计算与应用[22]。
1.1 模型假设
假设条件如下:
(1)注入流体视为不可压缩流体,其物性参数为定值;
(2)计算管网压力时,近似为稳态过程,忽略管道内流体瞬变带来的影响;
(3)注水站泵前压力视为定值,不考虑泵前压力变化。
1.2 目标函数
以注水管网运行方案能耗最低与注入偏差量最小为目标建立油田注水管网系统多目标运行优化模型。模型中I={1,2,…,imax}为注水管网系统中所有节点的集合,其中包括普通管网连接节点与注水泵站节点、注水井节点等特殊节点,注水泵站以集合IS表示、注水井以集合IE表示,IS,IE∈I;Ki={1,2,…,kmax}为第i注水泵站开泵方案集合,其中i∈IS;J={1,2,…,jmax}为注水管网系统中所有管段的集合。由于模型目标为管网运行能耗与注水井注入偏差量同时较小,为了将二者转化为一个目标函数,需要引入单位偏差量成本损失系数CF[23],将注入偏差量以成本费用形式具体量化衡量。模型目标函数转化为管网运行方案总成本最小minF=f1+f2,包括注水泵运行的耗电费用f1以及注水井实际注水量与需求注水量偏差造成的损失f2。
注水泵运行耗电费用等于每台注水泵能耗乘以电价,表示为
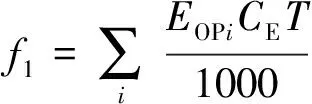
(1)
式中,EOPi为注水站i的输出功率,W;CE为电价,元/(kW·h);T为管网运行时长,h。
实际注水量与需求注水量偏差造成的损失为偏差量乘以单位偏差量成本损失系数,数学表达式为
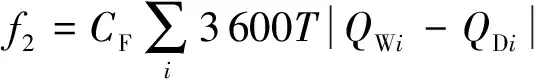
(2)
式中,CF为注水井单位注水偏差的费用系数,元/m3;QWi为第i注水井的实际注水量,m3/s;QDi为第i注水井需求注水量,m3/s。
式(2)中采用的绝对值表达在模型编程求解时需进行处理,处理具体形式如下:
M1i≥QWi-QDi,i∈IE;
(3)
M2i≥QDi-QWi,i∈IE.
(4)
式中,M1i和M2i为第i注水井注入偏差绝对值处理变量。
目标函数f2转化为
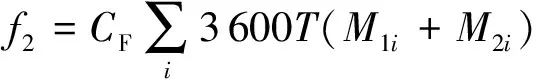
(5)
1.3 约束条件
将约束条件按照注水管网系统的研究对象分为注水站工艺约束、管网运行约束以及注水井工艺约束3类。
1.3.1 注水站工艺约束
注水站提供压力可表示为如下形式:
当FPSi,k=1,即节点i为注水站并运行第k种开泵方案时,节点i的压力为第k种开泵方案提供的扬程;当FPSi,k=0时,对节点i的压力不约束。数学表达式为
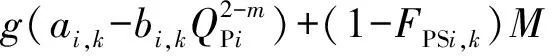
(6)
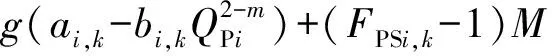
(7)
式中,pNi为节点i的压力,Pa;QPi为注水站i的过泵流量,m3/s;ai,k,bi,k为注水站i第k种开泵方案的扬程参数;ρ为水的密度,kg/m3;g为自由落体加速度,m/s2;m为泵扬程计算参数;FPSi,k为注水站开泵方案二元变量,若注水站i选择第k种开泵方案,FPSi,k=1,否则FPSi,k=0;M为极大值。
当节点i为注水站时,注水站i必须运行一种开泵方案,表示为
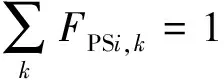
(8)
注水站输出的功率可表示为如下形式。当FPSi,k=1,即节点i为注水站并运行第k种开泵方案时,节点i输出的功率为第k种开泵方案的能耗;当FPSi,k=0时,对节点i输出的功率不约束。数学表达式为
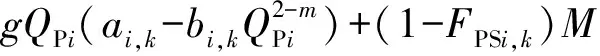
k∈Ki.
(9)
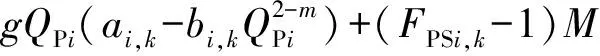
k∈Ki.
(10)
当FPSi,k=1时,即节点i为注水站且运行第k种开泵方案,注水站i注入管网流量即过泵流量需满足第k种开泵方案注入量上下限要求;当FPSi,k=0时,则对i节点注入流量不进行约束。具体形式为
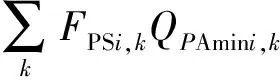
k∈Ki.
(11)
式中,QPAmini,k为注水站i第k种开泵方案的流量下限,m3/s;QPAmaxi,k为注水站i第k种开泵方案的流量上限,m3/s。
1.3.2 管网运行约束
研究对象为结构较复杂的环枝状油田注水管网系统,因此管段流量方向可能为正向或者负向,为正向时二元变量FQMj=1、FQNj=0,为负向时FQMj=0、FQNj=1。数学表达式为
FQMj+FQNj=1,j∈J.
(12)
式中,FQMj,FQNj为管段流向二元变量,管段j流量方向为正向时FQMj=1、FQNj=0,为负向时FQMj=0、FQNj=1。
当管段j的流量为正向即FQMj=1时,QTj大于等于0;当管段j的流量为负向即FQNj=1时,QTj小于0。具体约束形式为
QTj≥(FQMj-1)M,j∈J;
(13)
QTj<(1-FQNj)M,j∈J.
(14)
式中,QTj为管段j的管段流量,m3/s。
管段j流量满足其流量上下限要求:
QTIminj≤QTj≤QTImaxj,j∈J.
(15)
式中,QTImaxj和QTIminj分别为管段j的流量上、下限,m3/s。
与连接井口或注水站相连接的管段流量方向只能为正向,即当BWi=1与BEPi,j=1或BPi=1与BSPi,j=1时,FQMj=1。约束表达式为

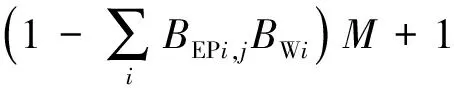
(16)
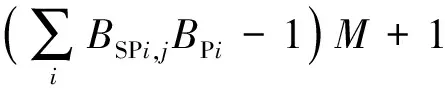
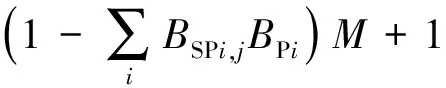
(17)
式中,BSPi,j为若节点i为管段j的起点,BSPi,j=1;BEPi,j为若节点i为管段j的终点,BEPi,j=1;BPi为若节点i为注水站,BPi=1;BWi为若节点i为井,BWi=1。
管网中各管段的沿程摩阻损失计算采用海曾威廉公式,具体计算表达式为
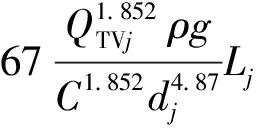
(18)
式中,pFVj为管段j的沿程摩阻绝对值,Pa;QTVj为管段j的管段流量绝对值,m3/s;Lj,dj分别为管段j的管长和管径,m;C为海曾威廉公式计算系数。
当管段j的流量为正向即FQMj=1时,管段j的管段流量QTj等于管段j的流量绝对值QTVj,管段j的实际沿程摩阻pFj等于管段j的沿程摩阻绝对值pFVj。数学表达式为
QTVj+(FQMj-1)M≤QTj≤QTVj+(1-FQMj)M,j∈J.
(19)
pFVj+(FQMj-1)M≤pFj≤pFVj+(1-FQMj)M,j∈J.
(20)
式中,pFj为管段j的实际沿程摩阻,Pa。
当管段j的流量为负向即FQNj=1时,管段j的管段流量QTj等于管段j流量绝对值QTVj的相反数,管段j的实际沿程摩阻pFj等于管段j的沿程摩阻绝对值pFVj的相反数。数学表达式为
-QTVj+(FQNj-1)M≤QTj≤-QTVj+(1-FQNj)M,j∈J.
(21)
-pFVj+(FQNj-1)M≤pFj≤-pFVj+(1-FQNj)M,j∈J.
(22)
管网中各管段水力工况匹配,管段j的沿程摩阻等于管段j的起点压力与管段j的终点压力之差,即当节点i为管段j的起点BSPi,j=1、节点i′为管段j的终点BEPi′,j=1时,管段j的沿程摩阻pFj等于两个节点压力之差。具体约束形式为
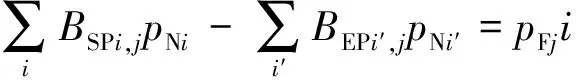
(23)
节点i的压力需满足管网系统的压力上下限,表示为
pmin≤pNi≤pmax,i∈I.
(24)
式中,pmax和pmin分别为管网系统压力上限和下限,Pa。
管网节点流量守恒,当节点i为管段j的终点,即BEPi,j=1时,节点i的流入流量为管段j的流量,若节点i为注水站,流入流量还包括注水站i的泵注入流量;当节点i为管段j的起点,即BSPi,j=1时,节点i的流出流量为管段j的流量,若节点i为注水井,流出流量还包括注水井i的实际注水量。具体约束形式为
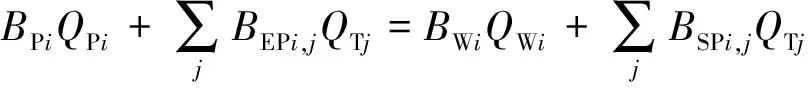
j∈J.
(25)
1.3.3 注水井工艺约束
注水井井口前一般均设有节流装置以满足井口压力要求,当节点i为注水井,即BWi=1时,井口压力pWi等于节点i压力pNi减去井口节流装置节流量pTi。数学表达式为
(BWi-1)M+pWi+pTi≤pNi≤(1-BWi)M+pWi+pTi,
i∈IE.
(26)
式中,pWi和pTi分别为第i注水井的井口压力和节流量,Pa。
当节点i为注水井,即BWi=1时,其实际注水量QWi满足注水量上下限要求。约束形式为
BWiQWFmini≤QWi≤QWFmaxiBWi,i∈IE.
(27)
式中,QWFmaxi和QWFmini分别为第i注水井的注入流量上限和下限,m3/s。
当节点i为注水井即BWi=1时,井口压力pWi与注水井实际注入量QWi需要满足吸水指数方程约束。具体形式为
(BWi-1)M+αiQWi+βi≤pWi≤(1-BWi)M+αiQWi+βi,i∈IE.
(28)
式中,αi,βi为吸水指数方程参数。
2 模型求解
采用蚁群算法结合线性近似、单纯形法的方式求解所建立MINLP模型,将模型中所有的离散变量作为蚁群算法食物浓度值评价函数的决策变量,在模型离散变量已知的条件下,可以将MINLP模型转化为NLP模型,此NLP模型最优解为该组离散变量的“食物浓度值”。针对NLP模型中变量之间的非线性关系,采用线性近似的方式处理,一定条件下转化将NLP模型为LP模型,最后采用求解LP数学模型最常用的基本方法单纯形法进行求解。求解基本流程如图1所示。

图1 求解流程示意图
Fig.1 Diagram of solving process
2.1 蚁群算法
针对大型环枝状油田注水管网系统所建立的运行优化数学模型中离散变量个数较多,若采用动态规划等数学规划算法求解,求解时间会成倍增长,求解效率极大降低。蚁群算法作为一种模拟进化算法,通过模仿蚂蚁寻找食物过程中发现路径的群体行为,具有自组织、正反馈以及较强鲁棒性等特点[24],能够较快收敛找到最优解,适合求解大规模组合优化问题[25-26]。因此采用蚁群算法优化模型中的离散变量计算效率高且适用性较好。
2.1.1 变量预处理
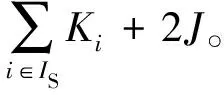
(1)规定变量FPSi,k之间须满足式(8)的关系,若不满足,则算法求解过程中加入惩罚函数。
(2)由于二元变量FQMj与FQNj之间存在固定关系,因此不必将FQNj加入决策变量中,可在模型求解完成后根据式(12)以及所求解FQMj计算得出变量FQNj。
(3)式(16)、(17)规定与注水站或注水井连接的管段流量方向为正,对应FQMj可不列入决策变量。
2.1.2 食物浓度函数
所建立注水管网运行优化模型以运行方案能耗成本与注水井注入量偏差损失成本之和最低为目标,为了满足蚁群算法食物浓度值函数最大化的要求,需将模型原有目标函数转化为极大化函数。在离散变量全部确定的条件下求解原MINLP模型对应的NLP模型的最优解,作为该组离散变量在蚁群算法中的食物浓度值。此外还需加入决策变量FPSi,k不满足式(8)约束以及NLP模型无可行解时的惩罚函数,表示为
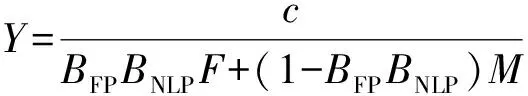
(29)
式中,Y为算法食物浓度值函数;F为注水管网系统运行方案总成本,元;M为极大值;BFP为FPSi,k是否满足式(8)约束二元变量,若不满足则BFP=0,若满足则BFP=1;BNLP为该组离散变量条件下对应NLP模型是否有可行解二元变量,若无可行解则BNLP=0,若有可行解则BNLP=1;c为常数,具体求解可设定不同值以食物浓度值函数Y为合适数量级。
2.1.3 问题转化与求解
将所建立数学模型中离散二元变量优化对应到蚁群算法中最优位置的确定,N维空间中的每一个位置代表数学模型中一组离散二元变量,将确定的一组离散二元变量代入模型中,求得NLP模型的最优解对应算法中该位置的食物浓度值,根据食物浓度值高低判断每个位置的优劣,最终找到食物浓度值最高的最优位置,即最优运行方案。具体求解步骤如下:
(1)设置算法基础参数,蚂蚁数量NuAnt、蚂蚁移动次数TAnt、挥发系数cvo、转移概率常数P0以及搜索范围上下限等,之后设置蚂蚁初始位置。
(2)根据食物浓度值计算函数,求解每个蚂蚁初始位置对应该组离散变量下的NLP模型的最优解,即该位置的食物浓度值。
(3)根据下式计算各蚂蚁状态转移概率,并根据食物浓度值判断其是否移动。
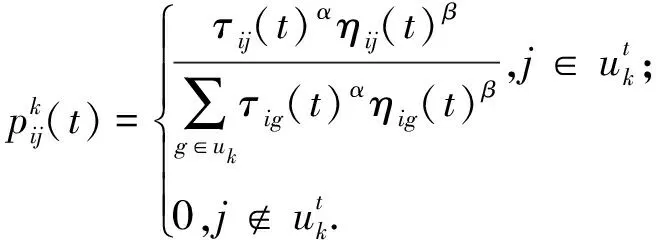
(30)

(4)所有蚂蚁进行一次移动之后,更新各位置信息量为
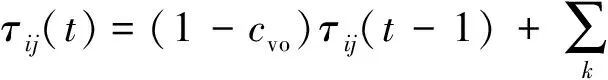
(31)
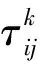
(5)所有蚂蚁完成所有移动后,寻找到食物浓度值最高的位置为数学模型最优解,即注水管网最优运行方案。
2.2 线性近似
在离散变量确定的条件下,原MINLP模型转化为对应NLP模型,约束条件中只包含连续变量的线性与非线性约束。通过线性近似方法将模型中非线性约束转换为线性约束,NLP模型转换为对应LP模型,之后采用单纯形法求解得到最优解。
2.2.1 基本思想
线性近似方法的主要思想为将模型中的等式与不等式非线性约束在某个已知初始点上进行一阶泰勒展开[27-28],非线性约束便转化为线性约束。其中已知初始点的确定至关重要,若初始点选取合适,近似误差能够控制在较小的范围内。具体形式如下:
minF(x)
s.t.Aeqi(x)≈Aeqi(xt)+Aeqi(xt)T(x-xt)=0,
i=1,2,…,Leqni;
Aj(x)≈Aj(xt)+Aj(xt)T(x-xt)≤0,j=1,2,…,Lni.
(32)
式中,F(x)为目标函数;Aeqi(x)为非线性等式约束条件;Aj(x)为非线性不等式约束条件;xt为已知初始点;Aeqi(x)为非线性等式约束方程梯度;Aj(x)为非线性不等式约束方程梯度;Leqni为非线性等式约束个数;Lni为非线性不等式约束个数。
2.2.2 模型求解
采用线性近似方法处理所建立油田注水管网系统运行优化模型中的连续变量非线性约束条件,即式(6)和(7)、式(9)和(10)与式(18)。在离散二元变量FPSi,k确定的条件下式(6)和(7)与式(9)和(10)可转化为
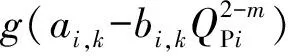
(33)
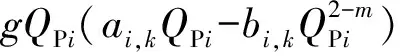
(34)
将式(33)、(34)与(18)在QP0i与QTV0j处一阶泰勒展开为
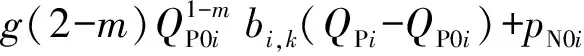
k∈Ki;
(35)

i∈IS,k∈Ki;
(36)
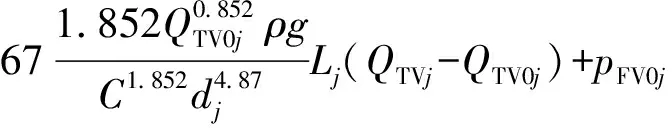
j∈J.
(37)
式中,QP0i为第i注水站注入流量初始点,m3/s;QTV0j为第j管段流量绝对值初始点,m3/s;pN0i为QP0i流量下泵提供的压力,Pa;EOP0i为QP0i流量下泵消耗的功率,W;pFV0j为QTV0j流量下第j管段沿程摩阻损失绝对值,Pa。
以式(35)、(36)、(37)代替原模型中的式(6)、(7)、(9)、(10)、(18),对应NLP模型便可转化为LP模型并采用单纯形法进行求解。为了确保求解最优解的准确性并将非线性方程线性处理的影响降到最低,对所涉及变量需采用迭代求解的方式,具体步骤如下:
(1)随机生成或者根据注水管网实际运行历史数据生成满足LP模型所有约束条件的QP0i与QTV0j,之后利用线性近似方法处理模型中非线性方程并采用单纯形法进行求解。
(2)判断所求得最优解中QPi、QTVj与计算之前已经生成的QP0i、QTV0j是否在一定误差范围内并符合收敛终止条件。
(3)若满足终止条件,所求得QPi、QTVj为模型最优解;若不满足,则令QP0i=QPi、QTV0j=QTVj并重复步骤(1)、(2)。
线性近似与单纯形法结合求解对应NLP模型程序框图见图2。
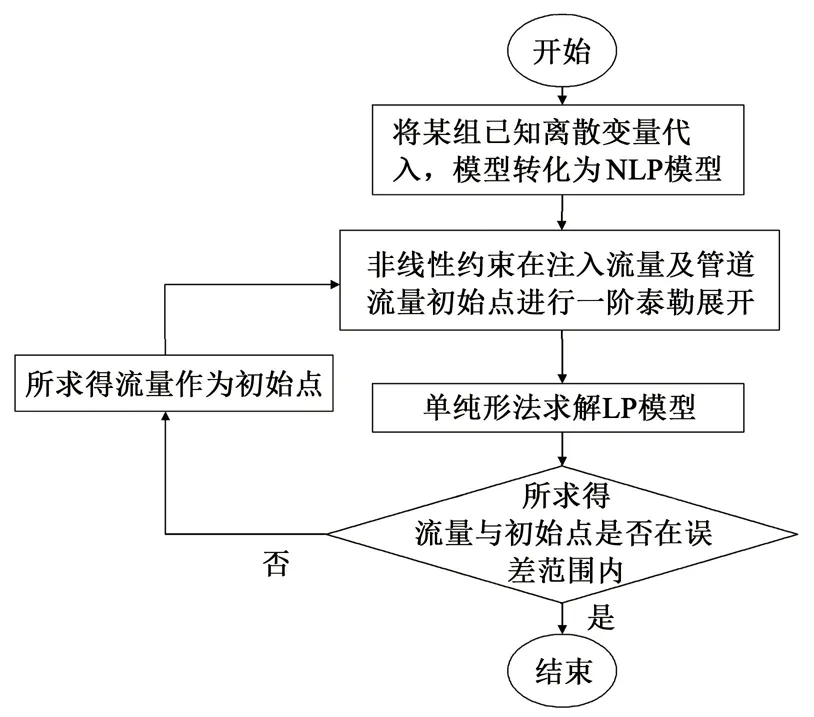
图2 求解NLP模型程序框图Fig.2 Block diagram of solving NLP model
蚁群算法与线性近似、单纯形法混合求解所建立大型环枝状油田注水管网系统MINLP模型程序框图见图3。
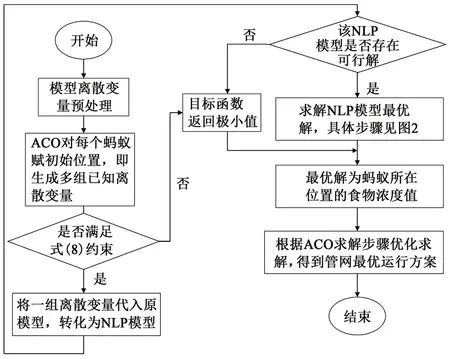
图3 求解MINLP模型总程序框图Fig.3 Block diagram of solving MINLP model
3 计算实例
以大庆油田第六采油厂某注水管网系统为例进行计算,管网拓扑结构如图4所示。共包含9座注水站、72个配水间、179条管段及514口注水井,属于大型复杂结构环枝状注水管网系统。图中红色方框代表注水站,绿色圆形代表配水间,数字编号为管网中各管段的编号,图中没有详细展示各注水井位置及其与相应配水间的隶属关系。
将实例代入所建立的注水管网运行优化数学模型,使用Intel Xeon E5-2630 v3(2.4 GHz) 电脑处理器,运用MATLAB R2015a软件编写计算程序。模型包含5 762个变量、13 568个不等式约束以及2 798个等式约束,属于大规模MINLP模型。采用提出的蚁群算法结合线性近似与单纯形法的求解策略进行求解,求解过程中蚁群算法基本参数赋值如下:蚂蚁数量NuAnt=200、蚂蚁移动次数TAnt=120、挥发系数cvo=0.85、转移概率常数P0=0.2。
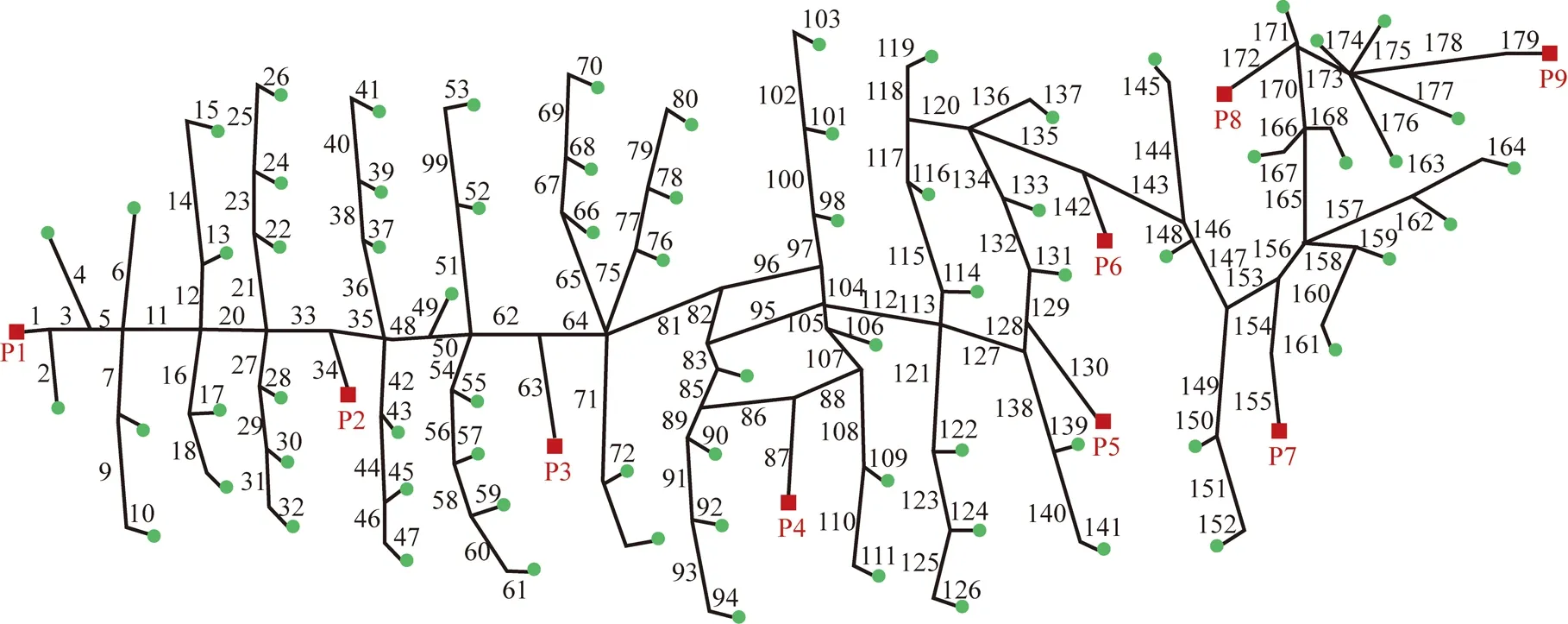
图4 注水管网拓扑结构图Fig.4 Topological structure diagram of waterflooding network
每个注水站配备若干台高压注水泵,泵具体参数如表1所示。

表1 注水站配泵参数
利用所建立数学模型及提出的优化求解策略对注水管网运行方案进行求解。计算用时194.22 s,求得各管段流量如图5所示。由于文章篇幅限制,选取部分注水井为例进行计算,其需求注水量与注入偏差量如图6所示。将求解结果与大庆采油六厂注水管网实际运行数据进行对比,部分井口注入偏差量对比结果如图7所示,对应井口节流压力如图8所示。井口节流量对比结果见图9。将注水管网基础数据代入文献[7]所建立的数学模型并采用混合遗传算法求解,求解耗时206.17 s,计算时间高出约6%。部分井口节流量对比结果如图10所示。
图5横坐标为各管段编号(对应图4管网拓扑结构图中管段编号),从图5中可以看出,各管段实际流量满足流量上下限要求,符合管网物料守恒基本规律。
图6中蓝色曲线代表各注水井需求注水量,纵坐标以图中右侧坐标轴表示;绿色线条代表注水井欠注,即实际注水量小于需求注水量;红色线条代表各注水井超注,即实际注水量大于需求注水量,纵坐标以图中左侧坐标轴表示。图7横坐标为各注水井编号,纵坐标为实注量与配注量偏差百分比,其中蓝色线条为现场各井注入偏差百分比,绿色线条为本文求得注入偏差百分比。从图7中可以看出,本文中求解各井实际注水量与需求注水量偏差量较小,平均注入偏差百分比为5.5%。并且对于大多数注水井而言,本文求解注入偏差量要小于现场实际注入偏差量,现场各注水井平均注入偏差百分比为8.6%。因此本文求解各注水井注入方案能够较大幅度降低注入偏差带来的损失,满足油田注水开发的正常需求,从而保证油田的稳定生产。
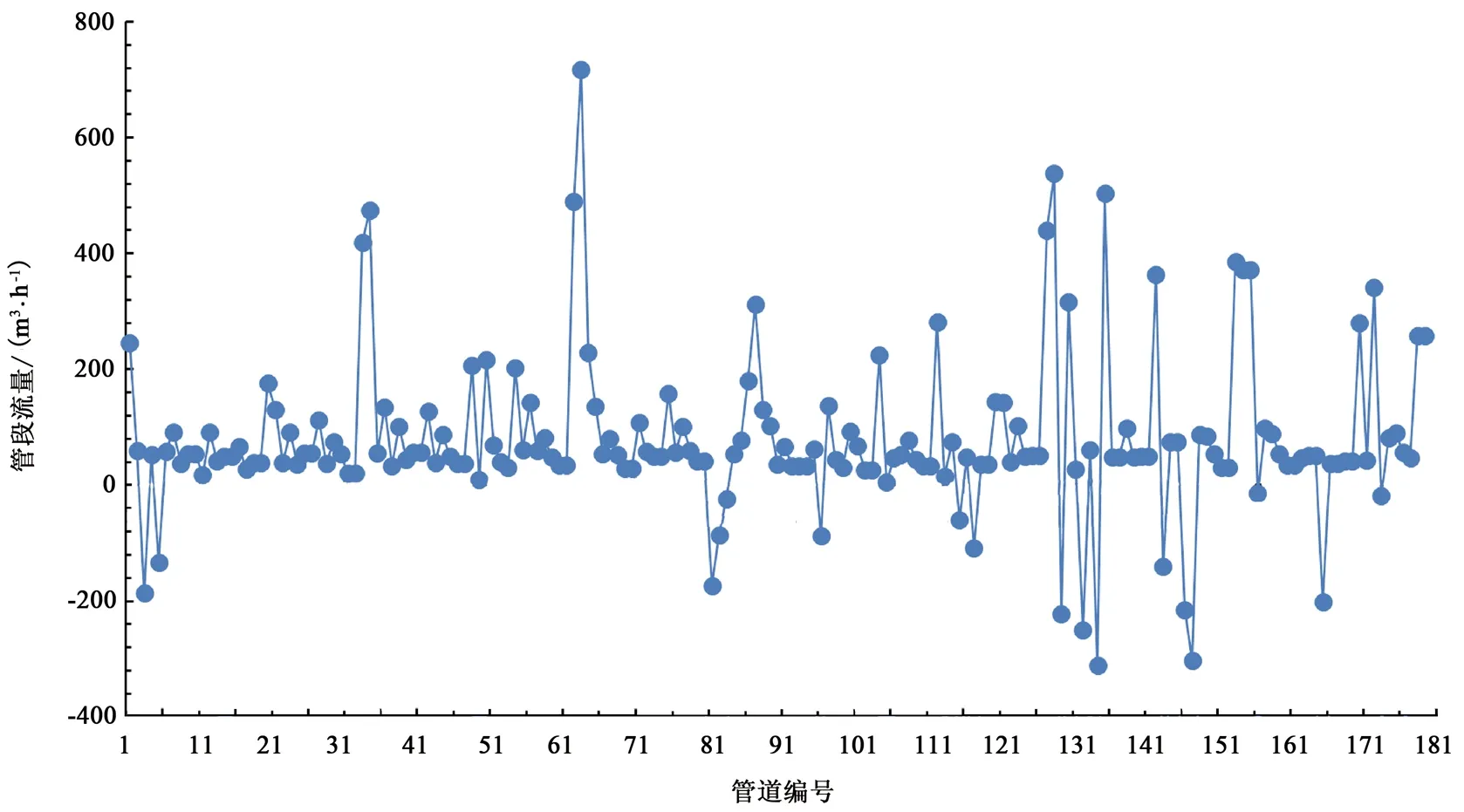
图5 管网中各管段流量Fig.5 Flowrate of each pipeline segment in network
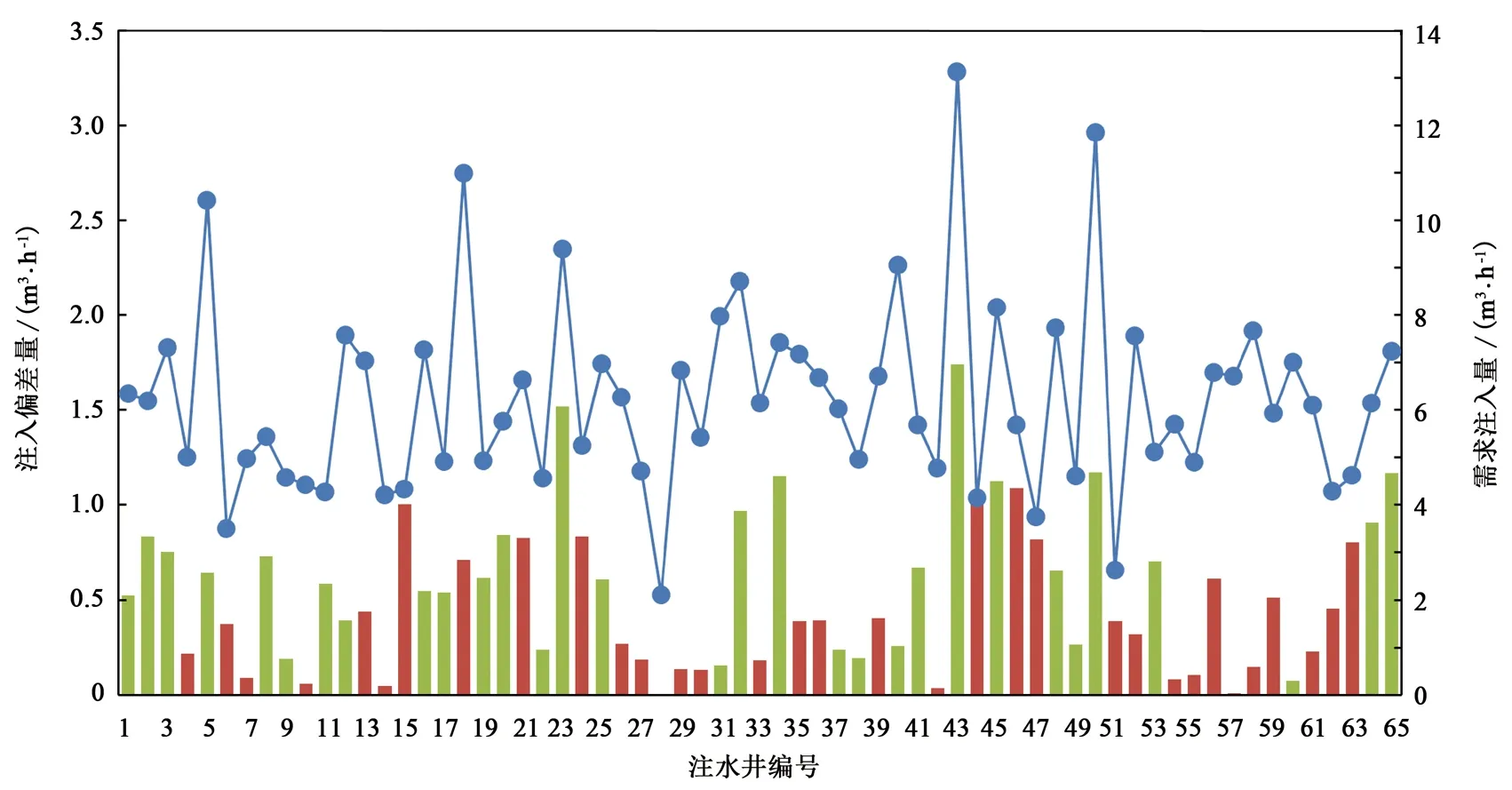
图6 各井需求注水量及注入偏差量Fig.6 Demand water injection and waterflooding volume deviation of wells
图8纵坐标表示各注水井井口压力节流量,图9、10纵坐标表示注水井节流量差值。图9中绿色线条代表各注水井现场节流量小于本文求解井口节流量;蓝色线条代表大于本文求解井口节流量。图10中红色线条代表采用混合遗传算法求得各注水井节流量小于本文求解井口节流量;蓝色线条代表大于本文求解井口节流量。从图中可以看出,本文所求得各井口节流量普遍小于现场运行数据与混合遗传算法求解结果。注水单耗从优化前现场6.25(kW·h/m3)降低到5.73 (kW·h/m3),相比于采用混合遗传算法优化制定注水方案,注水单耗也降低约6.3%;泵效率从优化前现场75.4%上升到78.7%,相比于混和遗传算法上升2.2%。因此采用本文中优化方式求解注水管网系统最优注入方案能够较大程度上节约能量,降低注水管网运行能耗,提高了管网运行的经济性。
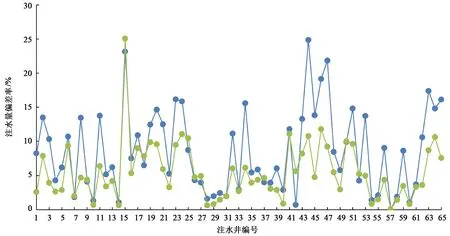
图7 部分井口注入偏差对比Fig.7 Comparison of waterflooding volume deviation of part wells
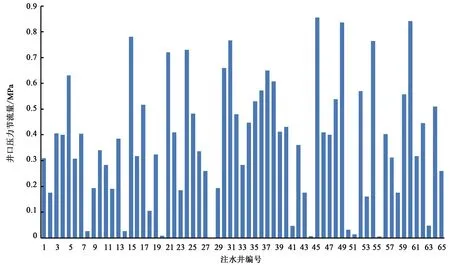
图8 井口压力节流量Fig.8 Throttling pressure of wellheads
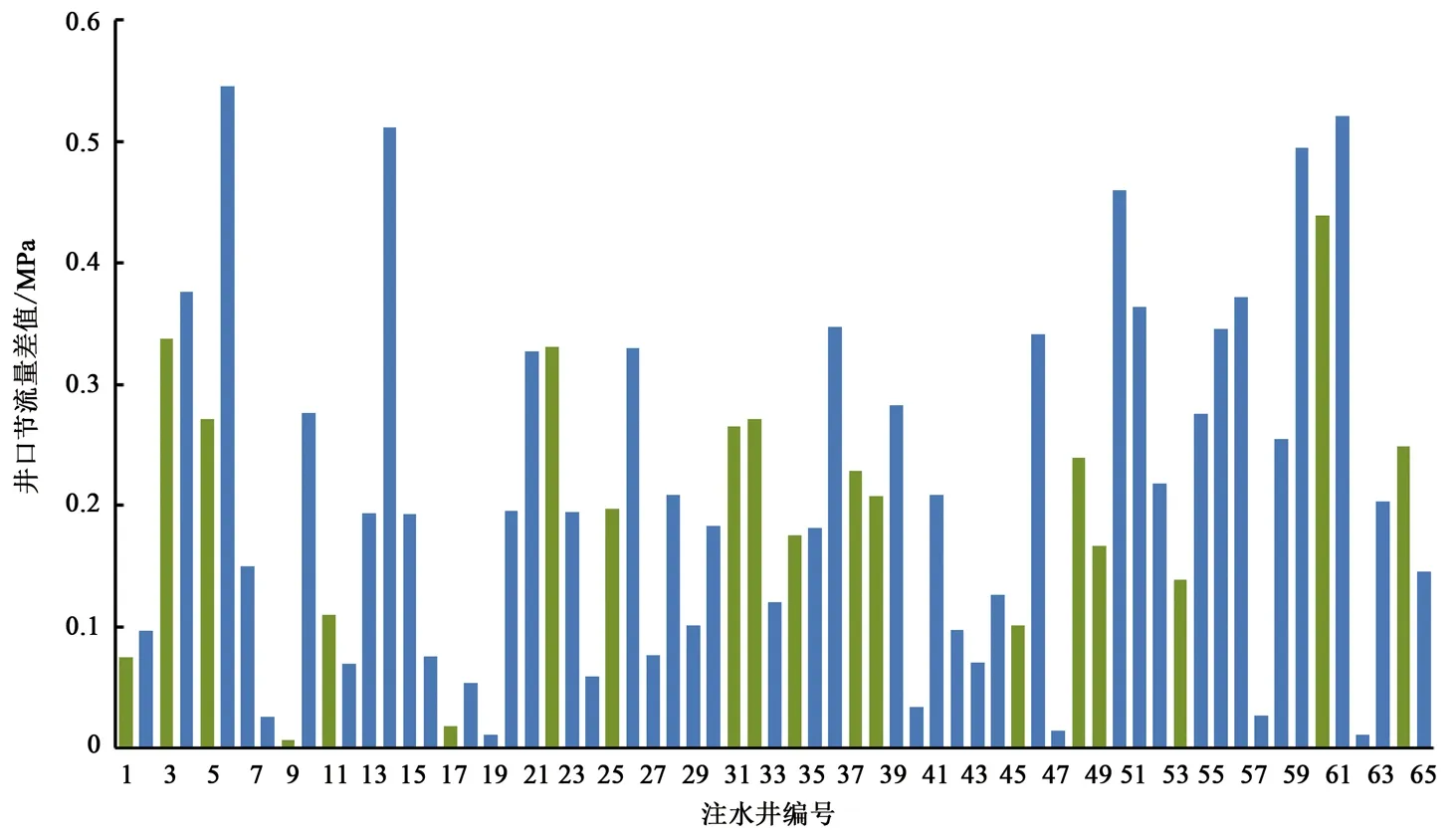
图9 与现场实际井口节流数据对比Fig.9 Comparison with throttling data of in-situ wells
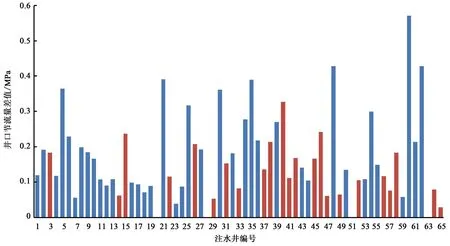
图10 与采用混合遗传算法求解结果对比Fig.10 Comparison with hybrid genetic algorithm
4 结 论
(1)针对所建立的大规模MINLP模型,提出的蚁群算法与线性近似、单纯形法混合分阶段求解策略保证了求解效率的同时较大程度地提高了此类模型求解结果的最优性,确保了运行计划的稳定性与经济性。
(2)所建立数学模型不局限于某个具体的注水管网系统,对其他实际液态介质输送管网系统运行方案的制定也有借鉴意义;所提出的求解策略不仅适用于注水管网运行优化模型,对其他较大规模MINLP模型的求解也具有一定的适用性。
