考虑热流固耦合干热岩储层热提取解析模型
2018-12-11樊冬艳张建光
樊冬艳, 孙 海, 姚 军, 严 侠, 张 凯, 张建光, 张 林
(中国石油大学(华东)石油工程学院,山东青岛 266580)
能源和环境是可持续发展战略的核心与关键,常规的化石能源已十分有限且不可再生,同时随着全球气候变暖,节能减排的呼声日益高涨,开发利用清洁的、可再生的新能源已成为各国21世纪的重要战略选择。地热能作为一种经济、可再生、环保的新型能源,在国际能源结构中所占比重越来越大[1]。中国地质科学院和中国科学院分别进行了中国干热岩资源量的估算,分别为2.5×1025J[2]和2.1×1025J[3],按照2%的回收率计算,为2010年能源消耗的4 400倍,因此中国对于干热岩地热开采和利用给予了极大重视[4-6]。干热岩储层的开采一般将低温水通过注入井注入热储层(人工裂缝和天然裂缝),经加热变成热水,再从生产井排出,实现地热的利用[7]。目前,研究干热岩裂缝内流动模型主要包括单裂缝模型[8]、连续介质模型[9-10]以及离散裂缝网络模型[11-13]等。其中单裂缝模型[8]假设水通过一个裂缝在注水井和生产井之间流动,实际储层存在大量裂缝因此与实际不太相符。连续介质模型[9-10]假设水通过均匀多孔介质在注水井和生产井之间流动,无法准确描述裂缝性质,因此存在一定的局限性。离散裂缝网络模型[11-13]假定储层由大量裂缝网络相互构成,更加符合实际情况。离散裂缝网络渗流模型的研究始于20世纪60年代对岩石水力学的研究,因此关于流动及流固耦合方面的研究已经非常完善[14-15]。目前地热多场耦合模型主要基于数值模拟方法,采用商业软件如TOUGH2进行数值模拟[16-18],而解析方法较少[19-20],主要以单条裂缝模型为主。笔者在考虑流体黏度及裂缝开度变化的情况下,建立基于离散裂缝网络模型干热岩热流固耦合开采数学模型,采用Laplace变换得到模型的解析解,以期为干热岩储层的开采提供技术指导及理论支持。
1 干热岩储层的离散裂缝网络模型
1.1 物理模型
由于干热岩储层地热资源的开采系统一般由热储层、注水井、生产井和压裂裂缝以及天然裂缝组成。冷水通过注水井注入热储层,基于热传导和对流等机制加热变成热水,再从生产井排出,实现地热资源的开发利用。为了准确模拟地热储层的热、流、固等复杂机制,针对干热岩储层采用离散裂缝网络模型(图1),其中采用一维的线单元代表二维的矩形裂缝,流体通过裂缝网络流动,基岩中无流体流动只进行热传导过程;离散裂缝内的流动为稳定渗流,应力通过改变裂缝的开度对流动产生影响,裂缝内主要以热对流为主;其次离散裂缝网络模型主要由注水井、生产井、边、结点构成,考虑了单井注入单井开采情况,只有相互沟通的裂缝参与流体流动,只与一个结点相连的裂缝无流体流动。
图1 干热岩储层离散裂缝网络模型Fig.1 Discrete fracture network model of dry-hot rock reservoir
1.2 离散裂缝模型的流动模型
为了研究裂缝中水的流动,基于质量守恒方程以任意一个结点n作为研究对象(图2),则流入与流出的质量应相等,当该结点为注水井时,定注入量生产,因此水的质量变化,即注水井的注入量minj已知,当结点为生产井时,定生产压力pw,该结点的压力已知。因此对于结点n可建立质量守恒方程为
(1)
其中

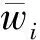
裂缝中的流动服从Poiseuille 流动规律,因此

(2)
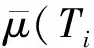
μw(T)=ATB.
(3)
其中
A=109.574-8.405 64S+0.313 34S2+8.722 13×
10-3S3,
B=-1.121 66+2.639 51×10-2S-6.794 61×10-4S2-5.471 19×10-5S3+1.555 86×10-6S4.
式中,S为水中矿物质质量分数,%;T为温度,1 ℉=[(T-32)×5/9]℃。
1.3 离散裂缝模型的开度模型
大量的实验和矿场实践表明裂缝开度在开采过程中具有动态性质[23-25],例如裂缝的开度受孔隙弹性和热弹性的影响,目前大部分模拟都没有考虑这些动态变化,笔者基于Ahmad Ghassemi 模型[26]在不考虑滤失的情况下给出裂缝开度在不同时间和位置随岩石特性和温度的变化关系为
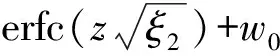
(4)
其中

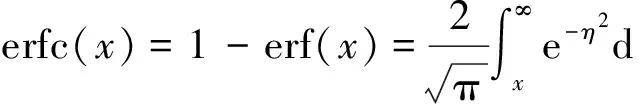
χ=αT(1+v)/(1-v),TΔ=T(x,z,0)-T(0,0,t).
式中,w为裂缝开度,m;w0为初始裂缝开度;z为沿裂缝方向的长度坐标,m;t为时间,s;erfc(x)为互补误差函数;χ为热弹性应力系数;αT为基岩的线性热膨胀系数,℃-1;v为排水泊松比;TΔ为初始时刻温度与端点的温度差,℃;Kr为岩石导热系数,W/(m·℃);ρr和ρw分别为基岩和流体水的密度,kg/(m3);Cr和Cw分别为基岩和流体水的比热容,J/(kg·℃);q0为注入流体速度,m2/s。
1.4 离散裂缝模型的温度模型
为了求解离散裂缝网络模型的流动,取任意一条裂缝i作为研究对象,由于假设流体只在裂缝中流动,沿着裂缝建立相应的坐标,如图2所示。
建立基岩中一维热传导数学模型为
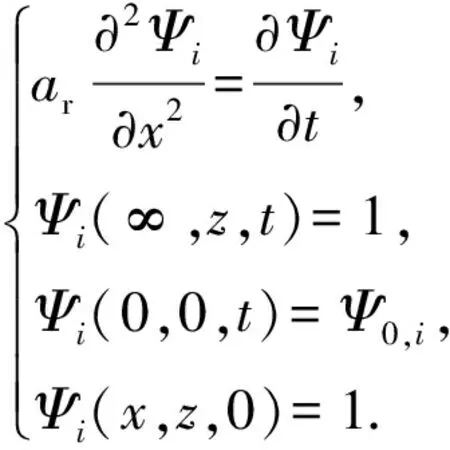
(5)
其中
Ψ=(T-Tw)/(Tr-Tw)i.
式中,Tr为初始储层温度,℃;Tw为注入水的温度,℃;ar为基岩的热扩散系数,ar=Kr/(ρrCr),故无因次温度的范围为[0,1]。
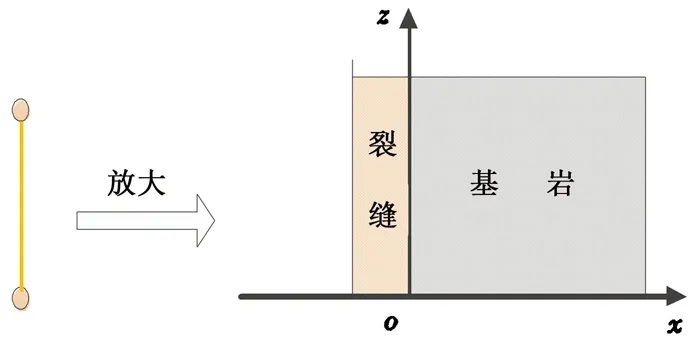
图2 单条裂缝坐标示意图Fig.2 Schematic diagram of single fracture
其次,裂缝中对流的流体在边界处,通过热传导的方式获取基岩中热量,忽略岩石与水界面阻力,假定水的温度与裂缝表面温度相等,即
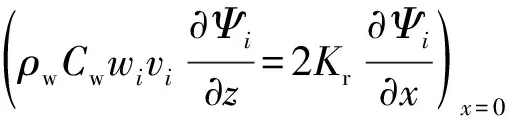
(6)
式中,wi为第i条裂缝的开度,m;vi为第i条裂缝的流速,m/s。
2 地热储层离散裂缝网络模型的求解
2.1 离散裂缝网络模型温度场求解
将一维热传导方程(5)、(6)变换到Laplace空间,则方程化为
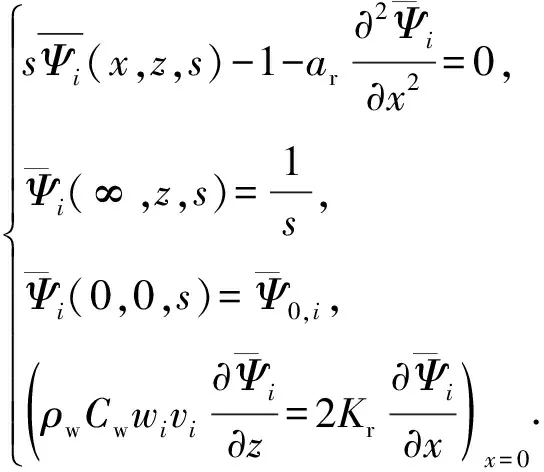
(7)
常微分方程的通解为

(8)
代入初始和边界条件方程(7)可得单条裂缝的温度分布为
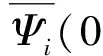
(9)
其中
当裂缝为离散裂缝网络时,第i条裂缝的初始温度由上一级裂缝j的温度决定,故
代入到方程(9)得:
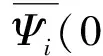

(10)



(11)
其中sk表示到达裂缝i的所有路径。
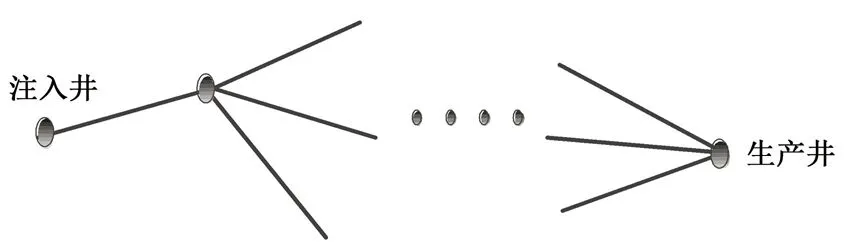
图3 注入井与生产井的多级裂缝网络示意图Fig.3 Schematic diagram for a multi-stage fracture network between injection wells and production wells
最后,将Laplace空间温度分布进行Laplace反演,得到实空间下裂缝网络中,任意一条裂缝的温度分布为
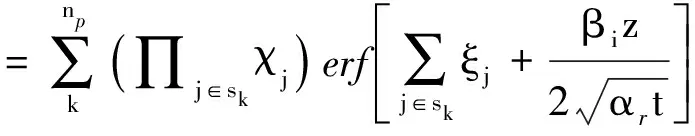
(12)
其中
2.2 离散裂缝网络模型耦合求解过程
为了说明离散裂缝网络模型的耦合求解过程,结合简单缝网进行说明,如图4所示。地热储层有一口注水井和一口生产井,注水井定注入量,生产井定生产压力,注入井与生产井通过6条裂缝、5个结点相连,其中裂缝1、2、5、6为水平缝,裂缝3、4为垂直缝,所有裂缝与地热储层垂直,简化为二维处理,把离散裂缝网络模型耦合求解过程分为以下3步。
(1)求解各边的流量分布。基于离散裂缝网络的流动模型,对质量守恒方程进行求解,其中黏度采用地层温度下流体黏度,开度取初始裂缝开度;计算得到各结点的压力值,通过压差计算各裂缝段的流量分布。如图4所示,包括注水井和生产井共有6个结点,通过方程(1)建立方程组DP=F,D为6×6的系数矩阵,P为各结点的压力值,F为流入流出量。
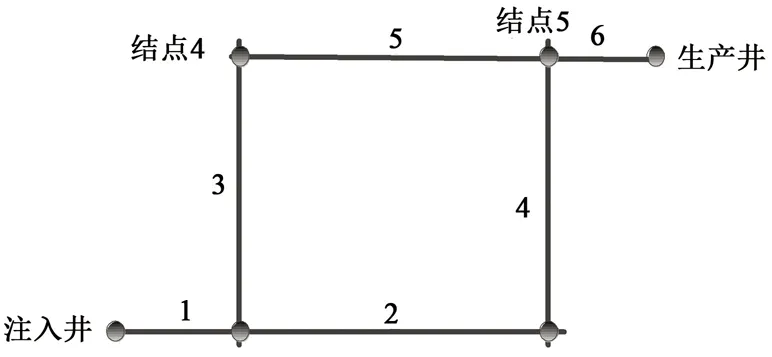
图4 离散裂缝网络实例1Fig.4 Discrete fracture network example 1
(2)求解各条边的温度分布。如果某条裂缝只和单个结点相连,则认为该裂缝中流体不流动,裂缝两个端点无压差;分析流入某裂缝的网络路径,如图4从注水井到生产井可能流动的路径为s1={1,3,5},s2={1,2,4},存在两条路径,代入式(12),则裂缝6的温度分布可表示为


(13)
(3)黏度及开度的耦合迭代求解。在上一步中得到各裂缝段的温度分布,通过式(3)得到相应水的黏度分布,代入式(4)计算开度变化,利用平均黏度和开度循环进行步骤(1)、(2)计算温度分布,直至平均黏度与开度的值稳定。
3 模型正确性验证及参数敏感性分析
为了验证本模型解析方法的正确性,在不考虑黏度及开度变化时,与TOUGH2数值计算结果进行对比,TOUGH2软件是由Berkeley 国家实验室研发的一款通用数值模拟器,针对裂缝及多孔介质中的多维、多相、多组分非等温流动过程,对离散区域采用有限差分,时间采用一阶向下全隐式方法[27],分析黏度及开度的变化对产水量的影响,以及热提取过程注入量和注入温度的影响。根据上述求解过程,对实例1(图4)进行求解,基本参数:裂缝1、6长度为100 m,裂缝2、3、4、5长度为500 m,裂缝初始开度为0.003 m,裂缝高度为1 m;水密度为980 kg/m3,水的比热容为4 300 J/(kg·℃);岩石矿化度为2 000 mg/L,岩石比热容为1 050 J/(kg·℃),岩石密度为2 700 kg/m3,岩石导热系数为2.7 W/(m·℃),泊松比为0.185;基岩的线性热膨胀系数为8×10-6℃-1。边界条件:注入量为0.1 kg/s;生产井定压力为10 MPa;注入水温度为10 ℃;储层初始温度为70 ℃。
3.1 模型的正确性验证
基于离散裂缝网络模型,在不考虑水的黏度及裂缝开度变化的情况下,计算实例1,将裂缝网络中各裂缝的温度分布与TOUGH2数值计算结果进行对比,如图5所示。本模型解析解结果与数值解TOUGH2计算结果吻合,生产井出口端早期误差约为3%,但随着时间增加误差减小,结果几乎一致,说明本解析模型的可行性及正确性,当然随着裂缝复杂程度的增加,误差稍有变化;其次各裂缝出口端的温度变化,随着时间的增加,出口端的温度逐渐降低,其中注水井裂缝1由于冷水的不断注入,温度下降最快,其次为裂缝2、3出口端,裂缝4、5出口端,裂缝6出口端即生产井处。
图6为实例1离散裂缝网络各点处的温度分布,包括生产1 a和生产10 a的两种情况。由图6可见,生产1 a时,生产井的温度还没有突破,产出井水的温度为70 ℃,而到了生产10 a整个裂缝网络系统的温度下降,由图6可见生产井热突破时间大约为3 a。
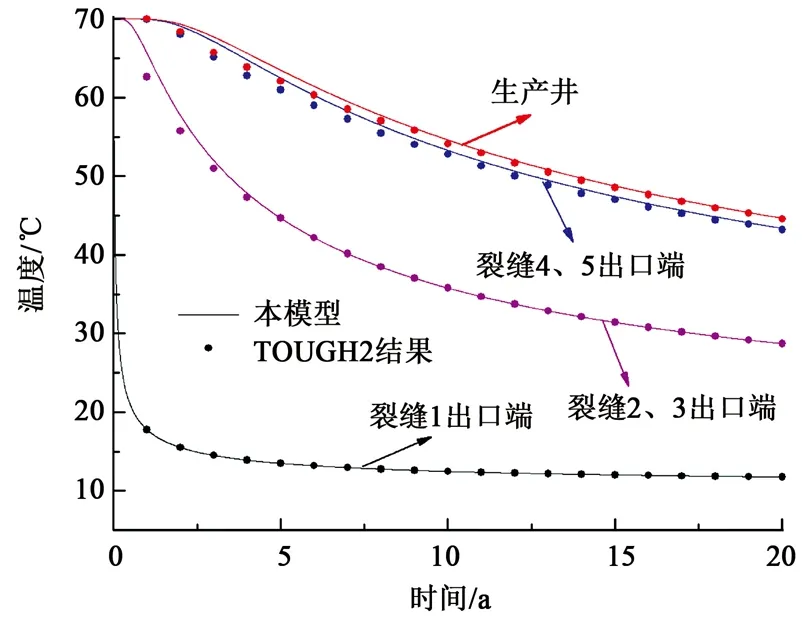
图5 解析模型与TOUGH2结果对比Fig.5 Comparison between analytic model and TOUGH2 results

图6 离散裂缝网络温度分布Fig.6 Temperature distribution of discrete fracture network
3.2 离散裂缝网络黏度及开度的影响
3.2.1 离散裂缝网络黏度
在地热储层随着冷水的注入,水的黏度随温度和压力的变化发生改变,特别是温度对黏度的影响较大,本文中假定水的黏度满足McCain公式,主要受矿化度及温度的影响。当不考虑水的黏度变化时,水的黏度通过注入水初始温度由式(3)计算得到,在实例1的基础上不考虑开度变化,计算各条裂缝的平均黏度,如图7所示。
由图7可见,随着时间的增加,各条裂缝内水的黏度增加,渗流速度减小,故出口端流量减小,趋于不考虑黏度变化时流量值;当不考虑黏度变化时,黏度由注入水初始温度(10 ℃)计算得到,黏度较大为1.368 mPa·s,随着冷水的注入,沿着离散裂缝分布,裂缝1最靠近注入端,因此裂缝1黏度与不考虑黏度变化时几乎重合,裂缝2、3与裂缝4、5位置对称,因此计算黏度相同,同时说明算法的正确性,沿着冷水由注入端至出口端,裂缝中水的温度逐渐上升,因此沿着水的流动方向黏度逐渐减小,但随着时间的增加,裂缝中水的温度逐渐降低,黏度逐渐增大,增加幅度越来越小,特别是早期黏度增加比较明显,晚期几乎不变,对于出口端流量在开采8 a后几乎没有太大的影响。
3.2.2 离散裂缝网络开度
地热储层基于离散裂缝模型,考虑孔隙压力及热弹性的影响,建立开度随温度压力的变化过程。在不考虑黏度变化的基础上,计算实例1得到各裂缝的开度变化,图8(a)为各裂缝在模拟20 a的过程中的平均开度随时间变化,图8(b)为考虑与不考虑裂缝开度的产量变化。
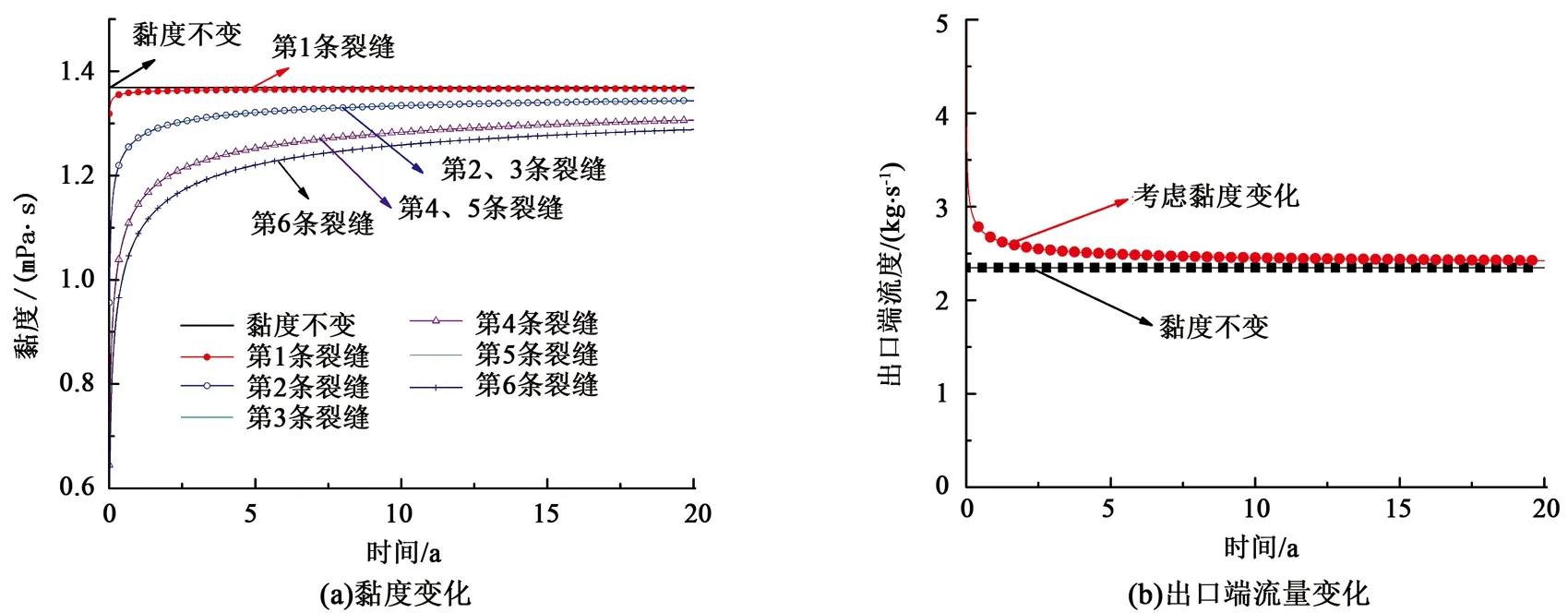
图7 考虑与不考虑黏度变化时曲线对比Fig.7 Comparison curves of considered viscosity change or not

图8 考虑与不考虑开度变化时曲线对比Fig.8 Comparison curves of considered fracture aperture change or not
由图8可见,随着时间的增加,各条裂缝的开度逐渐增大,同时出口端流量增加迅速,主要是由于裂缝的开度对流量的影响最大,裂缝开度的3次方为渗透率的函数,而流量直接取决于渗透率;不考虑开度变化时,设置开度为0.003 m,出口端流量较小;由于冷水的注入,受应力和热弹性的影响导致裂缝开度的增加,且沿着水流动的方向裂缝开度的增加幅度越来越小,即在注入端裂缝开度的增加最大,生产端裂缝开度变化最小。
3.2.3 同时考虑黏度及开度变化
通过以上分析可见,考虑黏度后出口端的流量变化不大,而考虑开度变化后出口端的流量增加明显,在此同时考虑黏度和开度变化时,出口端流量的变化规律。在实例1的基础上同时考虑黏度随温度的变化,开度随温度和地层性质的影响得到图9。
由图9可见,在不考虑黏度和开度变化时,出口端的流量为定值;考虑黏度变化后,早期流量变化明显,逐渐减小并趋于不考虑黏度变化时流量;考虑开度变化时流量迅速增加,主要因为裂缝的开度与流量成3次方关系,当同时考虑裂缝的开度变化和水的黏度变化时,产量依旧呈上升趋势,由图9可见相对而言裂缝开度对出口端流量的影响更加明显,因此在模拟过程中有必要考虑裂缝开度对地热储层的影响。
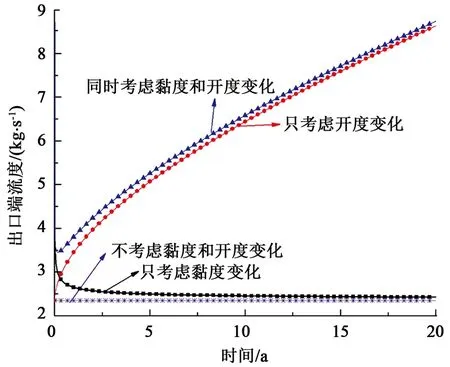
图9 对比不同因素出口端流量Fig.9 Export flow rates with different factors
3.3 注入量的影响
为了分析注入量对离散裂缝网络温度的影响,在其他参数不变的情况下,分别设置注入量为0.1、0.2和0.3 kg/s时,得到裂缝1出口端和生产井出口端处的温度变化,如图10所示。由图10可见,随着注入量的增加,裂缝1出口端和生产井出口端中水的温度逐渐减小,且随着注入量的线性增加,温度降低幅度越来越小,主要由于注入量增加,流体从地层带走的热量越多,裂缝中热量通过基岩块热传导越难及时补充。裂缝1出口端早期温度变化迅速,后期变缓;同时随着注入量的增加,生产井出口端热突破时间越来越早,因此在考虑热提取的过程中,不仅要考虑生产井流出水量,还需要综合考虑热水的温度及其他参数的影响,在各参数优化的情况下,选择合适的注入量,使产出热值实现最大化。
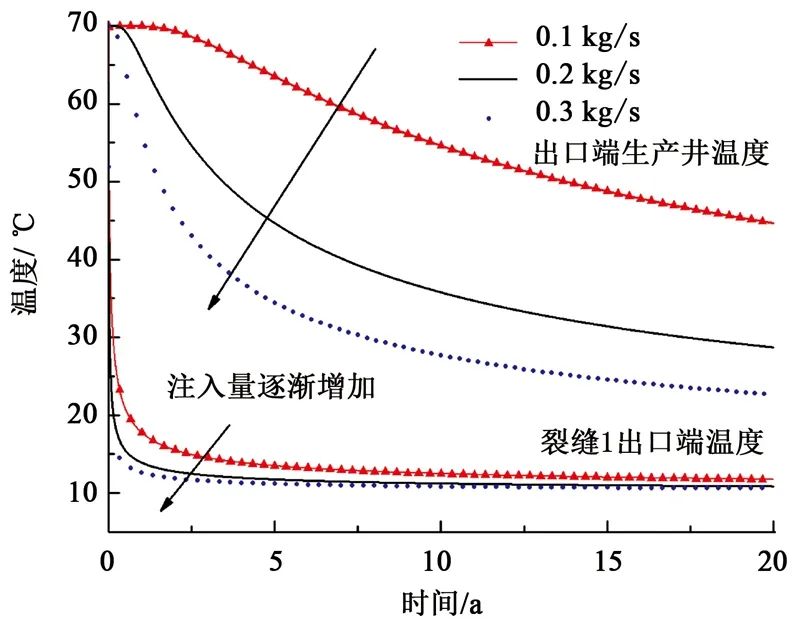
图10 不同注入量下生产井出口端温度变化Fig.10 Variation of temperature with injection volumeat production well outlet
3.4 注入温度的影响
为了分析注入水的温度对离散裂缝网络温度的影响,在其他参数不变的情况下,得到裂缝1出口端和生产井出口端处的温度变化,如图11所示。
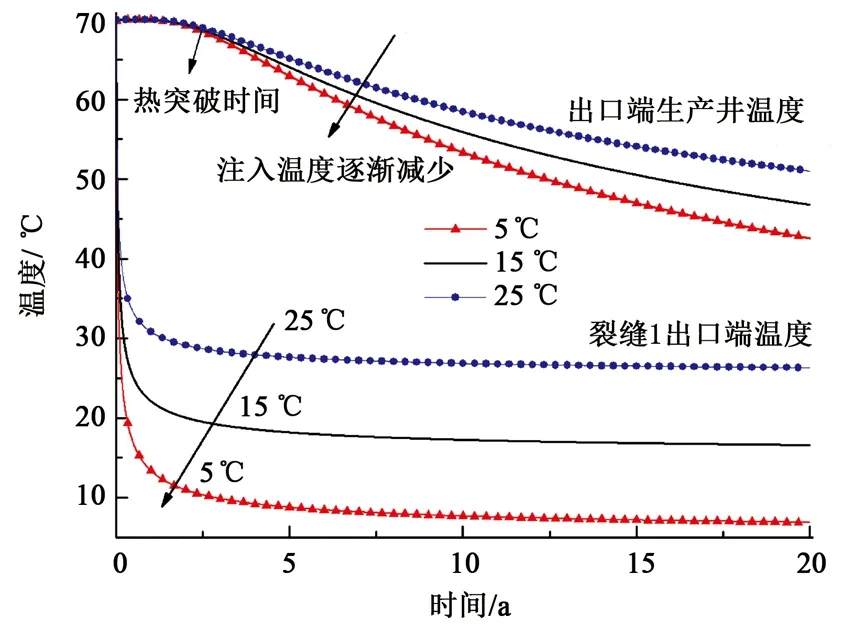
图11 不同注入温度下生产井出口端温度变化Fig.11 Variation of temperature with injection temperature at production well outlet
由图11可见,随着注入水温度的增加,生产井出口端处温度早期相同,到后期注入温度越低,出口端生产井温度下降越快,温度越低。在注入水量和裂缝网络结构相同的情况下,热损失近似,且由图11可见在不同注入温度下热突破时间几乎相同,受注入水温的影响不大,而主要受地层及裂缝网络的影响;其次随着注入水温度的线性增加,裂缝1出口端的温度早期迅速降低,并趋于相应的注入温度。
4 结 论
(1)随着时间的增加,各裂缝内水的黏度增加,同时出口端流量减小;当冷水由注入端流经采出端采出,裂缝中水的温度逐渐上升,沿着水的流动方向黏度逐渐减小,但随着时间的增加,裂缝中水的温度逐渐降低,黏度逐渐增大,增加幅度减小;黏度对流量的影响主要在早期,晚期影响较小。
(2)随着时间的增加,各条裂缝的开度逐渐增大,同时出口端流量增加迅速,主要是由于裂缝的开度对流量的影响较大;在同时考虑裂缝的开度变化和水的黏度变化时,产量依旧呈明显的上升趋势,故在干热岩模拟过程中不应忽略开度的变化。
(3)随着时间的增加,出口端的温度逐渐降低;随着注入量的增加,出口端中水的温度逐渐减小,且随着注入量的线性增加,生产井出口端中温度降低幅度越来越小;随着注入水温度的增加,出口端生产井处的温度早期相同,到后期注入温度越低,出口端生产井温度下降越快,温度越低,且在不同注入温度下热突破时间几乎相同,受注入水温度的影响不大。
