回归混合模型：方法进展与软件实现*

王孟成 毕向阳



回归混合模型：方法进展与软件实现*

王孟成1,2,3毕向阳4

(1广州大学心理系;2广州大学心理测量与潜变量建模研究中心;3广东省未成年人心理健康与教育认知神经科学实验室, 广州 510006) (4中国政法大学社会学院, 北京 102249)

近来以个体为分析对象的方法日益受到研究者的重视, 其中潜类别和潜剖面模型最为流行。研究者在潜类别和潜剖面模型建模时往往需要进一步探讨协变量与潜分组之间的关系(即带有协变量的潜类别模型)。例如, 哪些变量预测个体类别归属, 以及个体的类别归属对结果变量的预测。本文对近年来研究者提出的各种方法进行了回顾和比较。包括当结果变量是分类变量的LTB法; 当结果变量是连续变量时的BCH和稳健三步法。在此基础上, 文章为应用研究者提供了M软件示例, 并在最后对当前研究存在的问题和未来研究趋势进行了简要评价。

个体中心方法; 混合模型; 潜类别分析; 潜变量建模; M

传统的分析方法多以变量为分析对象, 例如因素分析(factor analysis, FA)将条目分成不同的因子或维度。近年来以个体为中心(person- centered)的方法逐渐引起心理学研究者的兴趣。其中潜类别分析(latent Class Analysis, LCA)和潜剖面分析(Latent Profile Analysis, LPA)是个体为中心分析方法中最基本也是最常用的分析方法(邱皓政, 2008; Collins & Lanza, 2010)。LCA在心理学、预防医学、精神病学、市场营销、组织管理等诸多领域已广为使用(e.g., 张洁婷, 焦璨, 张敏强, 2010)。

通常, 将LCA和FA作为测量模型, 因为两者都是处理潜变量和测量指标间关系的统计模型。与FA不同, LCA根据个体在观测指标上的作答反应将其归入特定的潜类别组(latent class)。然而LCA同FA一样, 也可以进一步拓展, 纳入协变量(预测变量和结果变量)。纳入协变量的FA即结构方程模型(Structure Equation Model, SEM); 纳入协变量的LCA称作带有协变量的潜类别模型以及更一般的形式——回归混合模型(Regression Mixture Modeling, RMM; e.g., Clark & Muthén, 2009)。例如, 考察性别、种族等人口学变量对潜类别分组的影响。本文首先对近年来提出的处理带有协变量的潜类别模型的新方法进行逐一介绍; 同时以一个具体的分析实例演示不同处理方法的分析过程。文章最后对当前研究存在的问题和将来的发展趋势进行简要评价。

1 潜类别模型

潜在类别分析或潜类别模型是通过类别潜变量来解释外显指标间的关联, 使外显指标间的关联通过潜在类别变量来估计, 进而维持其局部独立性(local independence)的统计方法(见图1) (邱皓政, 2008; Collins & Lanza, 2010)。其基本假设是, 外显变量各种反应的概率分布可以由少数互斥的潜在类别变量来解释, 每种类别对各外显变量的反应选择都有特定的倾向(邱皓政, 2008; Collins & Lanza, 2010)。与潜在类别分析非常相似的是潜在剖面分析, 区别在于前者处理分类变量, 后者分析连续变量。

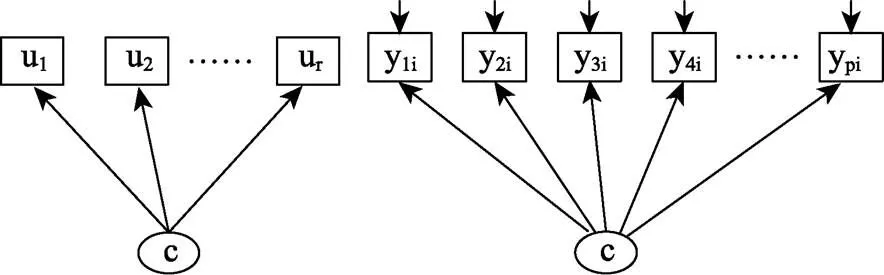
图1 LCA和LPA示意图

可以从方差分析的角度理解LCA。方差分析的特点是将方差分解成不同的来源, 常见的有组间vs.组内和被试间vs.被试内。在LCA中, 可以将方差分解为类别内和类别间(Sterba, 2013)。

根据局部独立性假设, 类别内的任意两个观测指标间的关联已通过潜类别变量解释, 所以它们之间已没有关联。根据独立事件联合发生的概率等于单独发生概率之积的原理, 在每个类别内部, 多个两点计分项目的联合概率可以表示为：

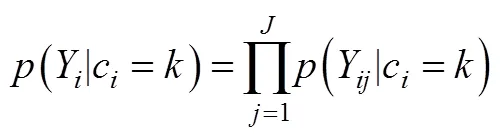
同时考虑多个类别水平时, 上式扩展为：

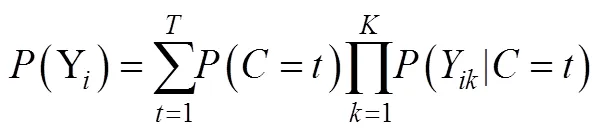
2 带有协变量的潜类别模型

在应用研究中, 研究者往往不仅关心将个体划分到特定的潜类别组, 而且希望探索哪些变量可以预测个体的潜类别分组或不同的潜类别分组如何预测重要的结果变量。这两种情况分别对应包含预测变量(predictor variable)的LCA和包含结果变量(outcome variable或distal variable)的LCA, 如图2所示。在左图中, 类别潜变量C由测量指标U测量; 左图中预测变量X指向类别潜变量C的箭头表示协变量影响个体类别归属。例如, 某研究试图了解人口学变量对儿童行为问题潜类别归属的影响, 根据5个测量儿童行为问题的指标将450名儿童分成4个潜类别组(即潜类别变量“问题行为”有4个水平), 然后做人口学变量(性别, 家庭经济地位和年龄等)对潜类别变量的回归模型。在右图中, 箭头的方向从潜类别变量C指向结果变量y, 表示类别属性(分类变量)预测结果变量。假设儿童问题行为潜类别归属可能会影响儿童学习成绩。由于成绩通常是连续变量, 所以此时为线性回归。也可以理解为不同问题行为类别的儿童学习成绩存在差异, 根据类别潜变量将儿童分成4组然后做方差分析。此时方差分析和线性回归等价。

在回归模型中, 通常是根据因变量的类型选择对应的回归模型。左图中, 类别变量C通常有2个及以上水平, 因此logistic回归和多项logistic回归是最常见的分析模型。右图的回归类型较为多样, 主要取决于y变量的类型, 可能是线性回归也可能是其他形式的回归模型。下面的介绍包含了两种不同协变量LCA的分析方法。

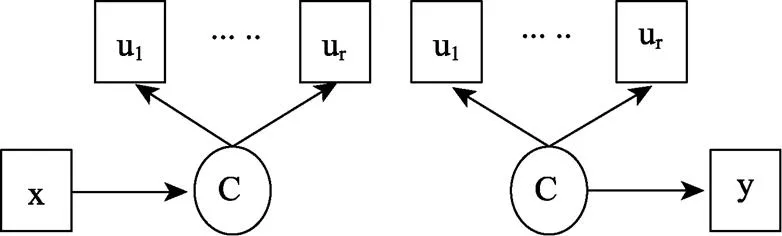
图2 回归混合模型示意图

2.1 包含预测变量的潜类别模型

总的来说, 带有预测变量的LCA的建模策略可以大致分成2大类：单步法和分步法(三步法)。顾名思义, 单步法在建模时一步完成所有模型(测量和结构)参数估计; 而分步法则采用逐步建模的步骤完成参数估计。

(1)单步法

单步法(one-step method)在处理带有协变量的LCA时, 同时完成潜类别分组(测量模型部分)和协变量关系建模(结构模型部分)。如果协变量是预测变量, 将其直接纳入模型进行分析, 协变量与潜类别变量的关系在LCA分析中同步完成。考虑协变量时的LCA表达式：

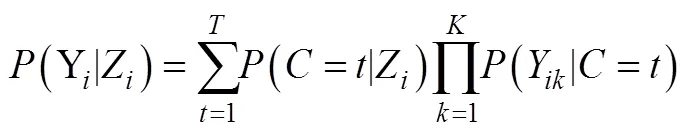
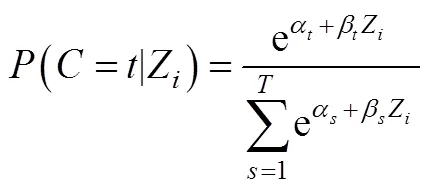
如果协变量是结果变量(图2右图), 只需将结果变量当作LCA的测量指标纳入模型(具体见后文)。然而单步法存在如下几点不足(Vermunt, 2010)：

首先, 当存在较多协变量时, 单步法的实际操作性较差。在探索性研究中, 由于缺少相关研究或理论预期, 模型中常常包含多个预测变量。在单步法中, 不同协变量的纳入和剔除都会影响测量模型(LCA)的结果, 使得整个分析过程非常繁琐。

第二, 模型建模困难。混合模型建模过程中最重要也是最复杂的问题是潜类别个数的确定, 包含协变量使得这一过程更加复杂。

第三, 单步法在实践中不易为应用研究者理解和掌握。回归混合模型的逻辑顺序是先根据LCA将样本分组; 接着以分组(潜)类别变量作为观测自变量或因变量进行回归分析, 而在单步法中这些过程是一步完成的, 理解和解释上较为抽象。

第四, 包含协变量的LCA模型可能会违反混合模型的前提假设如协变量在类别内的方差相等或/和正态分布等(Bauer & Curran, 2003)。

由于单步法的上述困难和不足, 分析过程清晰的三步法受到方法学者和应用研究者的广泛关注(e.g., Morin, Morizot, Boudrias, & Madore, 2011)。

(2)简单三步法

按照大多数应用研究者的分析习惯, 在做混合模型(mixture modeling)①分析时, 通常根据多个测量指标采用LCA将样本分成不同的潜类别组(测量模型部分)。然后将类别潜变量作为观测类别变量进行后续分析。常见的后续分析有：比较变量在潜类别组上的差异(独立样本检验或方差分析); 其他变量预测类别潜变量或类别潜变量预测其它变量。

三步法的一般分析过程如图3所示：(1)进行常规的LCA模型估计, 这一步只使用LCA的测量指标; (2)接着在第一步的基础上根据后验概率获得个体的类别归属变量即潜类别分组变量; (3)最后将潜类别分组变量作为观测变量(分类变量)连同协变量进行回归分析。

简单三步法也称作最可能类别回归法(Most Likely Class Regression; Clark & Muthén, 2009)②。这种方法符合应用研究者的分析习惯, 在实践中广为使用。

图3 简单三步法的分析流程

然而三步法也存在一些不足, 通常会低估类别潜变量和协变量的关系, 分类误差越大, 系数低估越明显(Bolck, Croon, & Hagenaars, 2004; Vermunt, 2010)。LCA分析的关键在于分类精确性。分类精确性对于个体中心的方法来说可以理解为测量信度或测量误差问题。如果分类误差较大, 把不属于某一类别的个体划分到该类别将会影响整个分析结果的准确性。针对简单三步法存在测量误差的问题, 近年来研究者提出了一些校正方法来减少分类误差产生的影响(Bakk, Tekle, & Vermunt, 2013; Lanza, Tan, & Bray, 2013; Vermunt, 2010), 下面将逐一详细介绍。

(3)概率回归法和加权概率回归法

这两种方法的分析过程与简单三步法类似, 也是分成三步。具体来说, 第一步依据观测指标将个体分类即执行LCA分析。第二步将个体的后验概率进行转换再做回归分析：(1)概率回归法将后验概率进行对数转换, 转换后的数值作为结果进行回归分析; (2)加权概率回归法则根据后验分类结果直接与协变量进行回归但采用后验概率进行加权。两种方法都考虑了分类的不确定性, 与简单三步法相比回归系数的结果相对较为准确, 但由于后验概率的估计本身也是存在误差的, 所以回归系数的显著性检验存在错误结论的可能(Clark & Muthén, 2009)。

(4)虚拟类别法

LCA根据一次分析的后验概率将个体分组, 这种做法存在抽样误差的问题③。虚拟类别法(pseudoclass method, PC法)采用类似缺失值分析时使用的多重插补法, 从个体的后验概率分布中随机抽取若干个(通常20次)可能的后验概率值④, 根据每次的概率值将个体分配到不同的类别, 然后平均若干次的结果作为最终的分类结果(Wang, Brown, & Bandeen-Roche, 2005)。

Clark和Muthén (2009)的模拟发现, 当分类精确性较高时(entropy > 0.8), 该方法表现较好; 然而在最近的模拟研究中发现, 与稳健三步法和单步法相比, 虚拟类别法在同等条件下表现最差 (Asparouhov & Muthén, 2014), 在实际应用中并不被推荐使用。

(5)稳健三步法或MML法

稳健三步法由Vermunt (2010)在Bolck等(2004)的研究基础上提出的。由于同时采用莫代尔分配法和极大似然估计, 因此又称作莫代尔极大似然估计法(Modal ML)。Asparouhov和Muthén (2014)将其称作三步法(3-steps approach), 为了区分简单三步法, 我们在这里将其称作稳健三步法。分析步骤同简单三步法, 区别在于第二步考虑了分类误差, 而简单三步法并未处理分类误差。稳健三步法⑤的具体分析步骤如图4。

图4 稳健三步法分析流程图(Asparouhov & Muthén, 2014)

稳健三步法最大的特点是在第二步考虑了分类误差或不确定性。假设W是基于模型估计的类别潜变量, 与实际的类别潜变量C并不完全一致(完全一致时不存在分类误差), 因此存在如下2个分类不确定率：

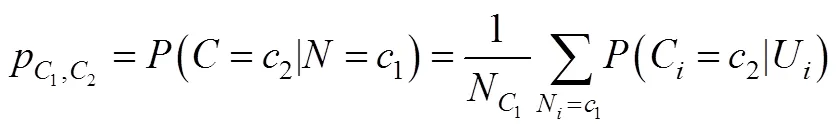
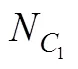
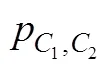
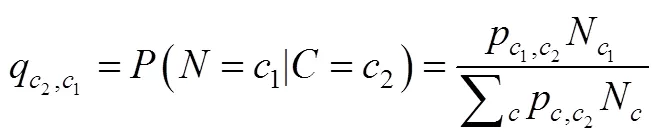
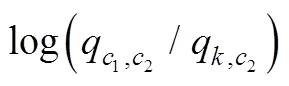
(6)修正的BCH法

BCH法最早由Bolck等(2004)提出, 用于处理包含分类预测变量的LCA。该方法与稳健三步法逻辑类似, 区别在于稳健三步法的第三步的估计方程采用极大似然估计, 而BCH将其转换成加权方差分析, 分类误差作为权重。

与稳健三步法相比, BCH法的一个突出优点是不会改变潜类别的顺序。潜类别顺序的改变是极大似然估计的一个“副产品”。由于ML估计常常得到局部最大化解而非整体最大化解, 所以混合模型估计通常设置多个起始值, 而起始值通常由软件随机生成, 所以每次分析的起始值不同得到的潜类别结果可能不同, 潜类别的顺序也可能不同。尽管使用相同的数据和指标, 所得到的拟合结果和类别数目也相同, 但类别潜变量水平的顺序可能不同(第一个类别变成第二个类别), 因此给潜类别分析带来很大的麻烦⑥。

BCH法的不足在于, 当类别距离很小以及小样本量时, 类别内的误差方差可能是负值。此时如果把类别内方差固定相等, 也可以获得正确的类别组内结果变量的均值(Bakk & Vermunt, 2016)。

就目前的模拟研究结果来看, 稳健三步法和单步法是处理来有预测变量RMM最好的方法。根据通常的潜类别建模流程, 首先确定群体分类, 然后再在此基础上做进一步分析。稳健三步法的分析过程清晰明确, 符合广大应用研究者的分析习惯而容易被接受。

2.2 包含结果变量的LCA

总的来说, 包含结果变量的LCA比包含预测变量的LCA要复杂一些, 因为在后者的建模过程中类别潜变量作为因变量只存在一种形式—— logistic或多项式logistic回归。但在包含结果变量的LCA中, 结果变量存在两种形式：连续和类别变量。下面分别介绍两种不同形式结果变量的LCA分析方法。

2.2.1 结果变量是连续变量

(1) 单步法

结果变量是连续变量时, 可以将结果变量当作LCA模型的指标, 同时完成模型估计。当局部独立性满足时, LCA表达式为公式2, 当纳入连续的协变量Z后, 公式2改写为联合的形式：

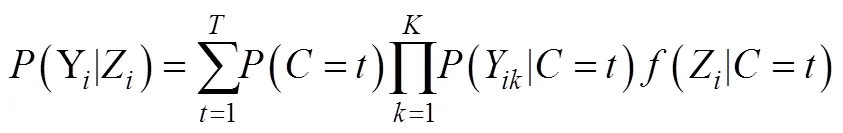
单步法需要满足重要的前提：连续结果变量在各类别内正态分布。如果正态假设不成立则会改变测量模型的结构及意义, 例如高估类别数(Bauer & Curran, 2003)。另外, 如果存在多个连续结果变量则更加复杂。假如采用每次只纳入一个结果变量的建模策略, 则会产生LCA模型混淆的问题：纳入不同结果变量间的LCA模型是不同的。

(2)LTB法

Lanza等(2013)最近提出了一种新的方法可以避免单步法违反假设时结果不准确的问题, 因为这种方法并没有特定的分布假设。在LTB法中, 首先将结果变量Z作为协变量纳入LCA分析(过程同包含预测变量的单步法), 流程如图5。

第二步计算结果变量在每个类别内的均值(连续变量)或概率(类别变量)⑦：

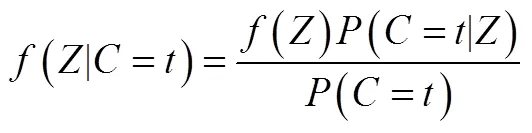
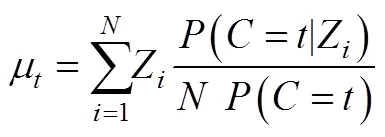
当连续结果变量的方差在不同类别内相等时即同方差(homoskedastic errors), LTB法的估计结果是无偏的, 此时结果变量与潜类别变量之间呈linear-logistic关系。如果同方差不成立即异方差(heteroskedastic errors)时, LTB法估计类别特定的均值存在偏差(Bakk & Vermunt, 2016)。另外, LTB方法处理多个连续结果变量时存在困难, 如果采用分别建模的方式将面临单步法同样的困境。

(3)修正的LTB法

针对LTB法的不足, Bakk等(2016)结合稳健三步法的分析思想对LTB法进行了修正, 并将其分成三步实现, 因此这种方法与稳健三步法分析过程非常相似(流程见图6)。首先, 使用测量指标建立LCA, 同时根据后验概率将个体分到不同的潜类别组N。第二步, 考虑分类误差的前提下通过估计潜类别变量C, 同时将结果变量Z作为协变量纳入分析(稳健三步法并未纳入协变量), 见公式11。

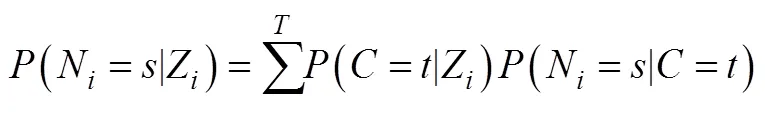
当连续结果变量的方差在不同类别内不相等时(类别内异方差), LTB法的估计结果是有偏的。

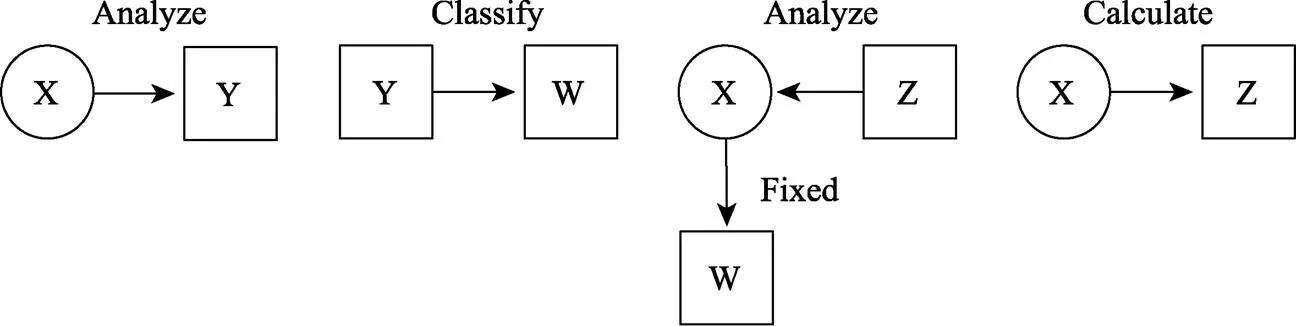
图6 修正的LTB法示意图

针对此问题, Bakk等(2016)提出在多项式逻辑斯特回归模型中加入二次项(公式12)来解决估计偏差的问题。

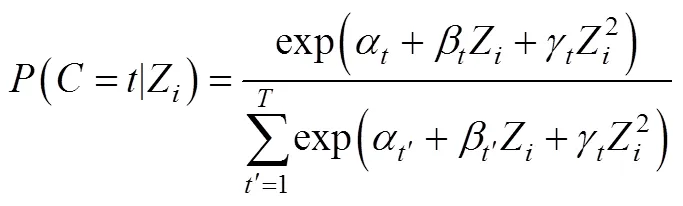
(4)修正BCH法

如前所述, BCH法⑧提出之初仅用于分析包含分类预测变量的LCA, 后来Vermunt (2010)对其进行了修正, 使其可以处理各种类型的变量。

(5)稳健三步法

稳健三步法也可以用于处理结果变量是连续变量的LCA。包含连续结果变量的LCA模型表达式变为：

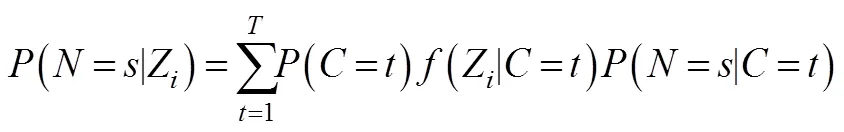
模拟研究发现(Bakk et al., 2013; Lanza et al., 2013), 当满足假设条件时⑨, 稳健三步法, BCH和LTB均可以得到无偏的参数估计结果(即类别特定的结果变量的均值)。然而, 当条件不成立时(非正态、方差不同质), 稳健三步法和LTB表现较差, 而BCH法则表现的很稳健(Bakk & Vermunt, 2016)。Asparouhov和Muthén (2015)通过模拟进一步比较了稳健三步法的两种变式(即类别等方差和类别不等方差; 分别对应M中的DE3STEP和DU3STEP), LTB法, 单步法, PC法和BCH法在连续结果变量非正态(双峰分布)时的表现, 结果进一步证实了BCH的稳健性(其他方法表现均不佳)。尽管如此, 当类别距离或分类精确性较小时(比如entropy = 0.5), BCH也会低估标准误。他们的结果还发现, 当组内方差同质性不成立时, 方差不等的稳健三步法(DU3STEP)和BCH法表现最佳, 且前者更优。

2.2.2 结果变量是类别变量

LTB法在处理分类结果变量时表现较好, 不会像分析连续结果变量时出现违反正态和方差同质假设后的估计偏差问题。在Asparouhov和Muthén (2014)的模拟研究中, 检验了3个样本量(N = 200, 500和2000)和2种分类精确性(entropy= 0.5和0.65)下LTB的表现, 结果发现仅在N = 200和entropy = 0.5时才会出现明显的偏差。

2.3 回归混合模型方法的适用情境汇总表

为了方便读者对上述介绍的各种方法间的比较和选择, 在Asparouhov和Muthén (2015)的基础上, 表1汇总了带有不同协变量LCA分析方法的使用条件和简要评价, 以便研究者选用。

3 实例分析

实例数据来自中国人民大学2010~2011执行的北京市城镇老年人(60~95岁)焦虑症状调查, 有效样本量1292⑩。本例中使用了其中的简版老年抑郁量表(GDS-15)总分(gds)、生活自理状况共16个题项(C2A-C2Q), 选项编码为：1. 不费力; 2. 有些困难; 3. 做不了)、年龄(连续变量)、“觉得自己现在老吗” (二分变量, ifold)等题目。

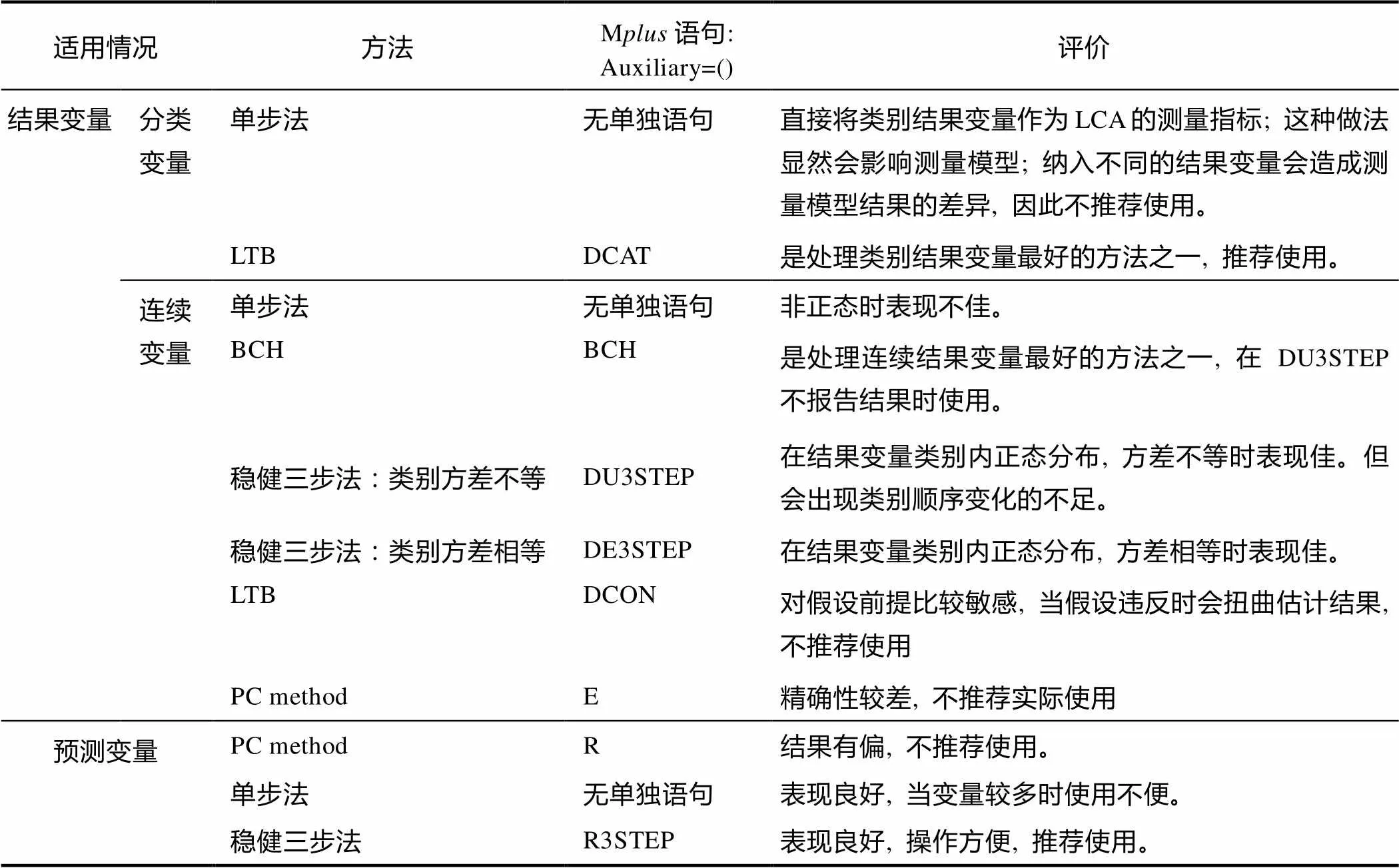
表1 各种情况处理方法汇总表

下面通过这个实例简单的介绍通过M软件如何执行上述各变量类型和方法。这里我们对生活自理状况量表进行潜类别分析, 然后依次加入预测变量和结果变量。

(1)潜类别分析

首先, 使用老年人生活自理状况量表的15个条目进行潜类别分析。分别拟合2~4个类别。通过模型比较后选择2个类别模型为最优模型(对应M语句见网络版附表1)。此时, Entropy = 0.965, 提示较高的分类精确度。根据条目的实际意义, 将两个类别分别命名为“不能自理类”和“能够自理类”, 分别占比15.3%和84.7%。图7呈现了两个类别的条件概率。

(2)加入预测变量的回归混合模型

在保留的两个类别模型基础上加入连续预测变量(年龄), 预测潜类别变量, 采用R3STEP法, 相应的M语句见网络版附表2。

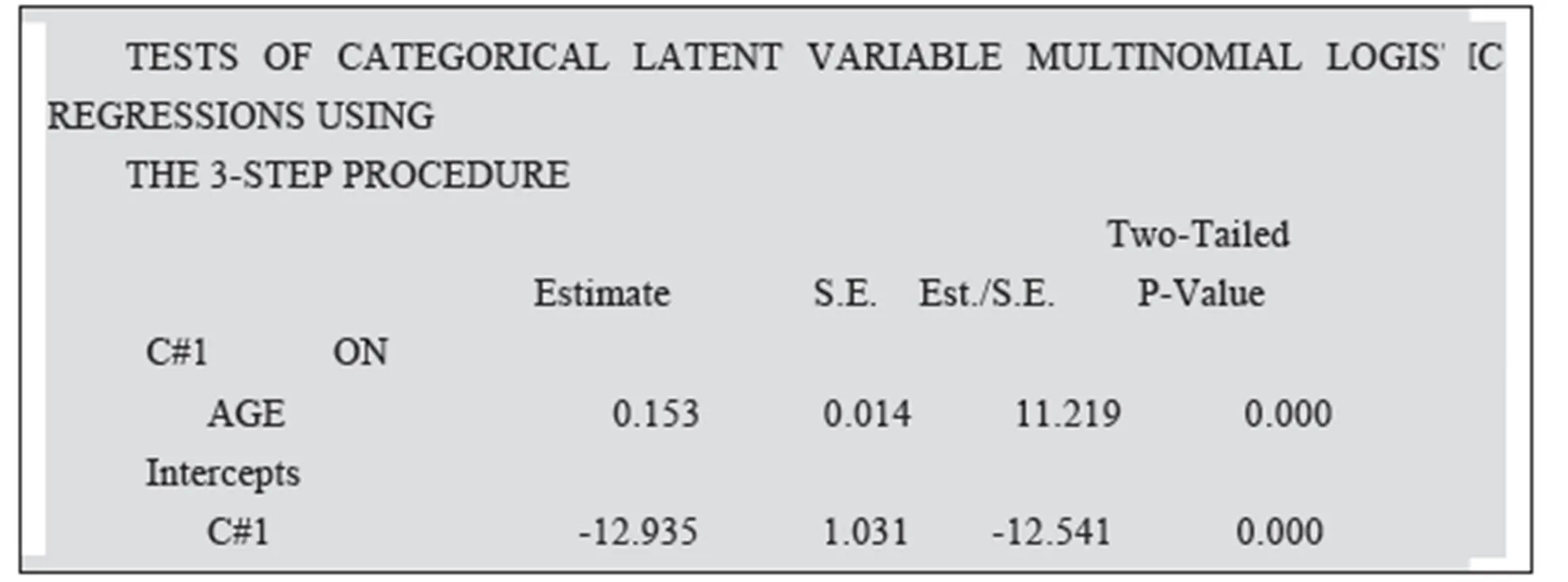
如前所述, 因变量为分类潜变量, 这里的回归方程为多项式logistic回归。软件默认第2个类别组为参照组(reference group)。结果表明(见网络版附表3)年龄对第一个类别的回归系数为0.153, SE = 0.014,< 0.001,说明年龄有助于预测老人所属的类别组。相对于第二类别组(可以自理组), 年龄每大一岁属于第一类别组(不能自理组)的发生比要高16.5%。

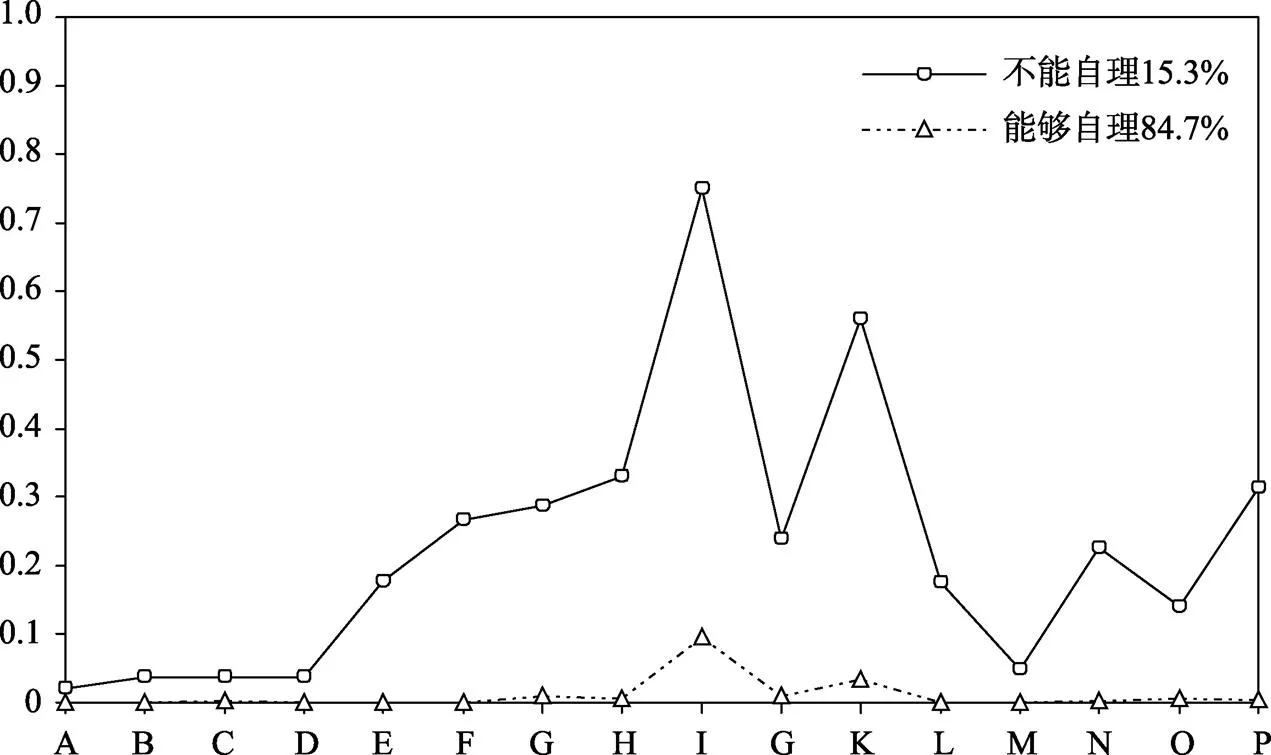
图7 两类别在选项3上的条件概率

(3)加入分类结果变量的回归混合模型

同样地, 在保留两个类别模型基础上加入自我感觉“是否老了”作为结果变量。该变量有2个选项, 所以采用DCAT法, 语句见网络版附表4。

分析结果表明(见网络版附表5), 相比于生活自理类别组, 生活不能自理类别的老人其“老人身份认同”的程度要高。具体结果是, 生活不自理类别组选择“觉得自己老了”的概率是0.735, “觉得自己未老”的概率是0.265; 而生活能自理组对应的选择是0.435和0.565。

(4)加入连续结果变量的回归混合模型

加入自评抑郁得分作为结果变量, 采用DCAT法, 语句见网络版附表6。两个类别组抑郁自评得分分别为：4.54和2.90, 差异显著(< 0.001)。此结果表明(见网络版附表7), 平均来讲, 生活不能自理的老人, 抑郁程度要显著高于生活能够自理的老人。

4 小结与展望

总的来说, 回归混合模型目前可以分为两大类别：带有协变量的潜在类别模型和混合结构方程模型。本文主要讨论的带有协变量的潜在类别模型的最新研究方法和软件实现。针对带有协变量的潜在类别模型又可以分成两种不同的类型：包含预测变量和结果变量的模型。就目前的方法学研究来看, 当结果变量是分类变量时, LTB法是最佳选择; 当结果变量是连续变量时BCH和稳健三步法是最佳选择。针对协变量是预测变量的潜在类别模型时, 稳健三步法是最佳选择。

混合模型作为潜变量建模的发展趋势之一, 到目前为止仍处在发展的初期, 很多方法都在探索阶段。尽管已有少数应用研究发表, 但总体来说目前应用研究尚不多。同样地, 回归混合模型作为混合模型的一个分支目前也还是个开放的研究领域, 多数方法是最近3~5年提出的, 而且更新的速度非常快。尽管本文介绍的都是最新的方法, 然而需要注意的是, 在处理不同协变量时所推荐的方法都是小规模模拟研究的结果, 尚需更多模拟研究验证拓展。

另外, 这些方法在处理实际问题时可能存在一些问题, 比如同时存在预测变量和结果变量的情景。在实践中这种情景还是非常普遍的, 但目前尚未有合适的方法。尽管如此, 回归混合模型作为新的方法为我们分析传统问题提供了新的视角。

邱皓政. (2008).. 北京: 教育科学出版社.

张洁婷, 焦璨, 张敏强. (2010). 潜在类别分析技术在心理学研究中的应用.(12), 1991–1998.

Asparouhov, T., & Muthén, B. (2014). Auxiliary variables in mixture modeling: Three-step approaches using M.,(3), 329–341.

Asparouhov, T., & Muthén, B. (2015)..MWeb Notes: No. 21. Retrieved from http:// www.statmodel.com

Bakk, Z., Oberski, D. L., & Vermunt, J. K. (2016). Relating latent class membership to continuous distal outcomes: Improving the LTB approach and a modified three-step implementation.,(2),278–289.

Bakk, Z., Tekle, F. B., & Vermunt, J. K. (2013). Estimating the association between latent class membership and external variables using bias-adjusted three-step approaches.(1), 272–311.

Bakk, Z., & Vermunt, J. K. (2016). Robustness of stepwise latent class modeling with continuous distal outcomes.(1),20–31.

Bauer, D. J., & Curran, P. J. (2003). Distributional assumptions of growth mixture models: Implications for overextraction of latent trajectory classes.(3), 338–363.

Bolck, A., Croon, M., & Hagenaars, J. (2004). Estimating latent structure models with categorical variables: One-step versus three-step estimators.(1), 3–27.

Clark, S. L., & Muthén, B. (2009).. Retrieved from http://statmodel2.com/download/relatinglca.pdf

Collins, L. M., & Lanza, S. T. (2010).. New York: Wiley.

Lanza, S. T., Tan, X., & Bray, B. C. (2013). Latent class analysis with distal outcomes: A flexible model-based approach.,(1), 1–26.

Morin, A. J. S., Morizot, J., Boudrias, J-S., & Madore, I. (2011). A multifoci person-centered perspective on workplace affective commitment: A latent profile/factor mixture analysis.,(1), 58–90.

Sterba, S. K. (2013). Understanding linkages among mixture models.(6)775–815.

Vermunt, J. K. (2010). Latent class modeling with covariates: Two improved three-step approaches.,, 450–469.

Wang C-P., Brown, C. H., & Bandeen-Roche, K. (2005). Residual diagnostics for growth mixture models: Examining the impact of a preventive intervention on multiple trajectories of aggressive behavior.(471), 1054–1076.

附录

附表1 潜类分析M语句

Title: Lantent Class AnalysisData: File is older_survey.dat ;Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gds agesq⑪; USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2);Analysis: TYPE = MIXTURE; Starts = 50 3; PROCESSORS = 4; !根据电脑情况指定PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*);Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14;

附表2 加入预测变量回归混合模型的M语句

附表3 加入预测变量回归混合模型输出结果(部分)

附表4 加入分类结果变量回归混合模型的M语句

附表5 加入分类结果变量回归混合模型输出结果(部分)

附表6 加入连续结果变量回归混合模型的Mplus语句

表7 加入连续结过变量回归混合模型输出结果(部分) ①混合模型比LCA和LPA更具一般的形式。 ②根据最大后验概率将个体分入到不同的潜类别组, 然后以该分组变量进行回归分析, 因此得名。 ③这里类似参数估计的点估计, 为了考虑抽样误差的影响通常采用区间估计。 ④因为存在分类不确定性所以抽取多个可能值作为分类误差。 ⑤在Mplus中, 稳健三步法有两种实现形式：自动和手动。自动形式只需采用AUXILIARY的R3STEP选项, 软件自动完成上述3步分析。手动形式需要分别执行两步分析。第一步, 单独执行LCA分析, 获得分类错误率的对数形式。第二步, 在这一步分析中, 将第一步保留的分组变量N的均值固定为分类错误率的对数值。 ⑥在稳健三步法分析中, Mplus自动监测顺序改变问题, 一旦发生顺序改变, Mplus将不报告结果(Asparouhov & Muthen, 2015)。 ⑦自变量是分类变量(这里的潜类别变量)因变量是连续变量的回归模型等价于单因素方差分析。 ⑧在Mplus里, 使用BCH分析包含结果变量RMM时非常方便, 只需一步即可实现, 例句见表2-8。 ⑨ ML和BCH假设连续结果变量在类别内的分布为正态分布。 ⑩参见中国国家调查数据库：http://www.cnsda.org/index. php?r=projects/view&id=60493698。感兴趣的读者可以自行下载数据尝试根据附表相应代码进行分析。 ⑪年龄平方项(/100) Regression mixture modeling: Advances in method and its implementation WANG Meng-Cheng1,2,3; BI Xiangyang4 (1 Department of Psychology, Guangzhou University; 2 The Center for Psychometric and Latent Variable Modeling, Guangzhou University; 3The Key Laboratory for Juveniles Mental Health and Educational Neuroscience in Guangdong Province, Guangzhou University, Guangzhou 510006, China) (4 School of Sociology, China University of Political Science and Law, Beijing 102249, China) Abstract: The person-centered methods, including latent class analysis (LCA) and latent profile analysis (LPA), are increasingly popular in recent years. Researchers often add covariate variables (i.e., predictor and distal variables) into LCA and LPA models. This kind of models are also called regression mixture models. In this paper, we introduce several new methods. Those methods include (1) the LTB method proposed by Lanza, Tan and Bray (2013) to model categorical outcome variables; and (2) the BCH method proposed by Bolck, Croon and Hagenaars (2004) to deal with continuous distal variables. Using an empirical example, we demonstrate the process of analyses in Mplus. The future directions of those new methods were also discussed. Key words: person-centered method, mixture modeling, latent class analysis, latent variable modeling, Mplus 分类号 B841 DOI： 10.3724/SP.J.1042.2018.02272 收稿日期:2017-03-04 * 国家自然科学基金(31400904); 广州大学“创新强校工程”青年创新人才类项目(2014WQNCX069); 广州大学青年拔尖人才培养项目(BJ201715)。 两位作者对本文贡献相同。 通信作者:毕向阳, E-mail: necessity@126.com; 王孟成, E-mail: wmcheng2006@126.com