多端直流电网限流电抗器的优化设计方案
2018-12-06龚雁峰
李 岩, 龚雁峰
(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)
0 引言
近年来,基于电压源型换流器的多端直流(voltage source converter based multi-terminal DC,VSC-MTDC)电网成为解决大规模风电、光伏等新能源并网的重要技术手段[1]。与两端柔性直流或传统直流电网相比,该技术在电能输送方面具有更好的灵活性、经济性和可靠性[2]。然而,由于直流侧的“低阻尼”特性,多端直流电网也面临着更为严峻的直流故障穿越问题[3]。
多端直流(multi-terminal DC,MTDC)电网的故障暂态发展极快,因此在实际工程中一般会安装合适的限流装置来抑制故障电流的上升速度[4-5],其主要功效为:①允许直流断路器(DC circuit breaker,DCCB)有更多的时间来隔离故障线路[6];②防止过流造成换流站内电力电子设备的损害[7];③减缓直流电压的跌落速度,提高故障穿越能力[8]。在目前已提出的限流装置中[6-12],限流电抗器(current limiting reactor,CLR)受到了广泛关注。它不仅能够有效抑制故障电流的上升速度,减小故障电流峰值,而且对系统稳态影响较小,造价也相对较低,因此已应用到MTDC电网的实际工程中[7]。
理论上,CLR越大,其抑制过流的能力越强,但大电感也给系统带来了诸多问题,如降低了系统的响应速度、容易诱发电压振荡[13]、增加系统成本等。此外,随着MTDC电网拓扑复杂、主设备约束增多,CLR的配置问题也越来越突出。文献[6]详细分析了限流电感对故障电流的影响,并提出了限流电感的计算方法,但该文仅考虑了直流断路器的约束条件。文献[7]从直流断路器和换流站闭锁角度,分析了张北MTDC电网的CLR配置方案,但该文缺少CLR的理论计算依据。文献[14]以系统配置电感最小和费用最低作为优化目标,提出了一种CLR的配置方法,但该方案仅适用于辐射状VSC-MTDC电网。
目前,MTDC电网的CLR配置仍缺少有效、可靠的理论方法,虽然采用仿真可以找到满足条件的电感值,但无法实现全局最优配置。此外,在配置CLR时,目前考虑的约束条件较为单一,缺少同时满足多重主设备约束的计算方法。为此,本文以最具前景的模块化多电平换流器(modular multi-level converter,MMC)型MTDC电网为研究对象,提出了一种通用的CLR优化设计方案。该方案实现了系统总电感最小的全局最优配置,并且同时考虑了直流断路器、换流站闭锁和保护需求三方面的约束,保证了系统在故障穿越期间能够连续、可靠地运行。本文提出的设计方法适用于不同的电网拓扑和配置方案,能够为实际工程中的CLR选择提供有价值的理论依据。
1 MTDC电网极间短路故障建模
短路电流计算是CLR的设计基础,在优化过程中需要进行上百甚至更多次的暂态计算,采用完整的MTDC电磁暂态模型计算故障电流十分耗时。因此,为提高CLR的优化效率,本文采用MTDC电网等效模型来计算故障电流。
设计CLR应考虑系统可能发生的最严重故障类型,因此本文以极间短路为例进行建模分析。图1所示为本文采用的测试系统。
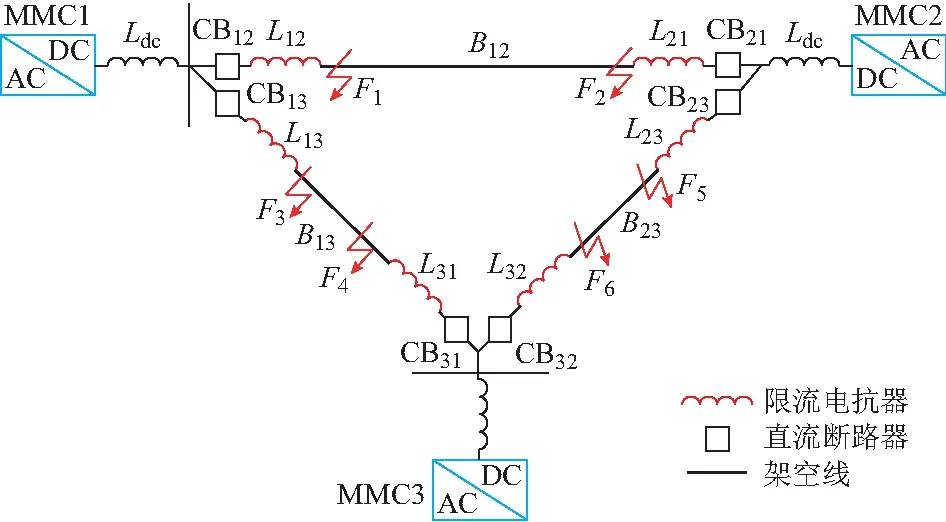
图1 测试系统Fig.1 Test system
假设在线路B12出口发生金属性极间短路故障F1,在不考虑换流站闭锁条件下,其等效电路如附录A图A1所示。Li,Ci和Ri(i=1,2,3)分别表示换流站i的等效电感、等效电容和等效电阻,且满足
(1)
式中:R0为桥臂电阻;∑Ron为所有子模块通态电阻(包括绝缘栅双极型晶体管(IGBT)和反向二极管)的总和;L0为桥臂电感;NSM为每个桥臂的子模块个数;C0为子模块电容;Ldc为换流站出口的平波电抗器电感值。
根据附录A图A1中的等效电路,可以快速建立系统的状态方程[15]:
(2)
式中:i为支路电流矩阵;u为换流站等效电容电压矩阵;矩阵A,R,L和P的建立方法详见文献[15]。测试系统在故障F1条件下,各支路电流仿真值和计算值的对比如附录A图A2所示,可以看出,等效模型能够准确地反映出故障电流。
2 CLR配置的约束条件
传统的CLR设计方案考虑因素较为单一,缺少对系统多重主设备限制的综合考虑。因此,本节以保证系统在故障穿越期间连续、可靠运行为宗旨,分别从直流断路器、换流站闭锁和保护需求三方面进行深入分析,并提出CLR配置的约束条件。
2.1 直流断路器
保证直流断路器的可靠动作是CLR配置的最基本任务,在直流断路器的动作时间(包括继电保护动作时间和故障电流开断时间)内,任何故障的短路电流均不能超过直流断路器的最大中断电流。因此,约束条件可以表示为:
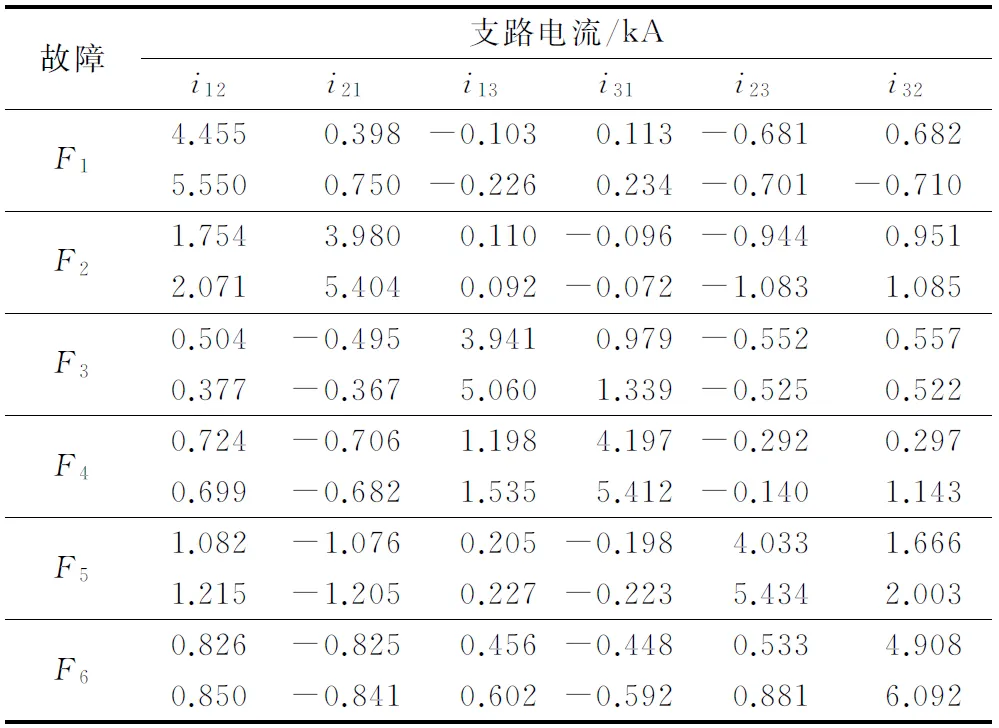
|iij(tb)| (3) 式中:iij(t)为线路Bij中的故障电流;imax为直流断路器的最大中断电流;tb为从故障发生到故障清除的时间。 在设计CLR时,直流断路器一般作为已选好型号的一次设备,其最大中断电流imax可视为常数。故障清除时间tb则受故障距离、保护性能和直流断路器等多个因素影响。下文将以一次完整的保护动作时序为例进行说明(假设系统配备了快速行波保护装置),如图2所示。 图2 MTDC系统保护时序图Fig.2 Protection sequence of MTDC system 在图2中,故障起始于t0时刻,初始故障波将在t1时刻到达线路保护终端。保护装置在t2时刻检测到故障,然后在t3时刻完成区内故障判定,并马上向直流断路器发出跳闸指令。直流断路器在t4时刻完成故障线路隔离。从图中可以看出,从故障发生到完全隔离的全部时间可以近似表示为: tb=Δtd+Δtp+Δtr (4) 式中:Δtd为初始故障波从故障点到保护装置的传播时间,其大小由故障距离lf和波速v决定,且满足Δtd=lf/v;Δtp为行波保护的动作时间,包括故障检测时间Δtp1和故障区间判别时间Δtp2,其大小由保护性能决定;Δtr为直流断路器的动作时间,其大小由直流断路器的性能所决定,以目前被广泛关注的混合型直流断路器为例[5],其动作时间约为2~3 ms。 为实现故障穿越期间系统的连续运行,CLR应保证桥臂电流始终小于其过流保护阈值。故障期间桥臂电流的准确计算十分困难,传统的配置方法均是通过仿真来验证所选参数是否满足条件。而本节通过深入分析桥臂电流与电容电压的关系,间接提出了CLR的约束条件。 若忽略桥臂中环流的影响,桥臂电流、交流电流和直流电流的关系可以近似描述为[16]: (5) 式中:ipj和inj分别为j相的上、下桥臂电流;ici为换流站i出口处的直流电流;ij为j相交流电流。可以看出,桥臂电流主要由交流电网电流和直流电流叠加而成。 首先分析整流侧的桥臂电流。以换流站1和故障F1为例,故障起始于0.5 s。图3分别给出了换流站1的每一相子模块电容电压和ucj(j=a,b,c)、交流电流ij和桥臂电流直流分量idc(idc=ici/3),以及每一相上、下桥臂电流ipj和inj,其中un表示额定极间电压。 图3 F1故障时换流站1的电容电压、交流电流和桥臂电流Fig.3 Capacitor voltages, AC currents and arm currents at MMC1 under fault F1 从图3中可以看出,短路故障发生后,子模块电容电压立即开始下降,直流电流idc立即开始增加,但此时交流电流并没有立即发生改变,上、下桥臂电流幅值增大主要由直流成分增加所致。然后,子模块电容电压继续下降,系统逐渐失去对交流输出控制,交流电流开始逐渐增大。当子模块电容电压下降至0或很小时,交流系统将完全或近似呈现三相短路状态(或进入不控整流阶段)。可以看出,桥臂电流与子模块电容电压密切相关,当电容电压跌落不大时,交流系统不会出现明显的过流现象。 下面分析逆变侧桥臂电流的变化规律。以换流站2和线路B12末端的双极短路故障为例,图4给出了换流站2内相关变量的变化规律。从图4中可以看出,逆变侧由于放电电流和原电流的方向相反,因此在故障发生后,桥臂电流中的直流分量和交流分量的幅值首先减小,然后开始反向增加。虽然逆变侧换流站桥臂电流的变化规律与送端不同,但同样可以看到,当子模块电容电压跌落不大时,交流系统不会出现明显的过流现象。 图4 F2故障时换流站2的电容电压、交流电流和桥臂电流Fig.4 Capacitor voltages, AC currents and arm currents at MMC2 under fault F2 采用附录A图A1所示的等效模型无法计算桥臂电流,但通过本节的分析可知,当电容电压跌落不大时,交流电网馈入电流不会发生明显变化,因此可以根据这个特性来估计故障期间桥臂电流的最大值。此外,防止故障穿越期间直流电压跌落过多也是MTDC电网连续运行的必要条件。因此,可以得到如下约束条件: uci(tb)≥kminun (6) (7) 式中:uci为换流站i的等效电容电压;kmin为比例系数;iac为换流站内交流系统相电流幅值;iarm,th为桥臂电流过流保护的阈值;kac为可靠系数。 直流线路保护对设计CLR的影响主要体现在两个方面:①保护性能会影响直流断路器的动作时间,这一点已在2.1节中进行了分析;②如果系统采用了基于CLR的保护算法,其大小应满足保护的可靠性需求。 快速、可靠的直流线路保护一直是制约MTDC电网发展的重要因素,由于CLR形成了直流线路的有效边界,为保护难题的解决提供了重要的突破口。近年来,学者们已提出了多种基于CLR的保护设计方案[17-21],但无论哪种算法,均需要一定大小的CLR来保证算法的可靠性。因此,若系统采用了基于CLR的保护设计,在选取线路上的限流电感Lij时应满足: Lij≥Lp,min (8) 式中:Lp,min为保护算法需要的最小电感值。 大电感会降低系统的响应速度,并会增加工程的投资成本(尤其是对于海上换流站),因此本文以系统配置的限流电感总和最小作为优化目标。系统电感应包括各直流线路上电感和各换流站出口电感之和,因此优化目标可以表示为: (9) 式中:f为目标函数;Ldci为换流站i出口处的平波电抗器电感值。 为保证故障期间系统的连续、可靠运行,CLR需同时满足直流断路器、换流站闭锁和保护需求三方面的约束条件。根据第2节的分析结果,得到约束条件如下: (10) 理论上,约束条件应考虑系统可能发生的所有故障,但计算所有的故障场景十分耗时,也完全没有这个必要,只需要保证CLR在最严重故障情况下能够满足条件即可。一般而言,当线路出口发生极间金属性短路故障时,临近直流断路器和换流站将面临最为严重的短路故障,因此可以定义测试系统的6种最严重故障F1~F6,如图1所示,并分别建立其对应的等效电路和状态方程。 然后确定F1~F6的故障清除时间,即式(10)中的tb。以故障F1为例,仍考虑最严重的情况,即保护和直流断路器的动作时间均取最大值,本文以Δtp=2 ms,Δtr=3 ms为例。根据式(4)可知,在故障发生约5 ms后,故障电流将被完全中断。为提高系统的可靠性,在优化时应考虑一定的裕度,因此本文将以tb=7 ms为例。若其他线路也配备了相同性能的直流断路器和保护装置,那么故障F2~F6的最大故障清除时间均以7 ms为例进行优化。 最后一步是采用优化算法确定CLR的全局最优配置。本文以“教与学”优化(teaching learning based optimization,TLBO)算法[22]为例,该算法模拟以班级为单位的学习方式,具有收敛速度快、全局搜索能力强、无须调节学习因子等优点。当然,采用其他性能较好的优化算法同样能够满足设计要求。附录A图A3为本文优化流程,其具体步骤如下。 (11) 在每次随机生成一个学员Xi后,需要检验其是否满足约束条件,检验方法如下:将学员Xi中的限流电感值分别代入故障F1~F6的状态方程中,计算得到tb时刻各支路电流、电容电压和桥臂电流,并检验其是否均满足式(10)中的约束条件。如果满足条件,则继续生成学员Xi+1,否则将重新执行式(11),直至生成满足约束条件的Xi为止。 随机生成完N个初始学员后,将确定初始班级中的教师。根据式(9)计算初始学员的目标函数向量f=[f1,f2,…,fN],将其中最小值fi对应的Xi作为教师Xtea。 步骤2:迭代寻优。在生成初始班级学员后,TLBO算法将进入迭代寻优过程,每一次的迭代过程都包含教师教学和学员相互学习两个阶段。 1)教师教学阶段 在该阶段,班级中的每个学员Xi根据Xtea与学员平均值之间的差异进行学习,公式如下: (12) (13) 在更新完学员之后,需要检验新学员Xi是否满足约束条件。计算满足约束的新学员Xi的适应度fi,并按照以下逻辑更新: (14) 2)学生相互学习阶段 在该阶段学员Xi随机选择一名班级中的其他学员Xj进行交流,并根据他们之间的差异进行学习,公式如下: (15) 在完成以上两个更新步骤后,重新计算学员的目标函数向量f=[f1,f2,…,fN],并将其中最小值fi对应的Xi更新为教师Xtea。 步骤3:检验是否满足结束条件。若迭代次数nite小于最大迭代次数nmax,则执行nite=nite+1,并转至步骤2继续进行迭代,否则优化结束,此时Xtea为最优解。 基于PSCAD软件搭建图1所示的测试系统。系统采用对称单极结构,换流站采用半桥子模块拓扑,并采用架空线路(依频参数模型)进行连接。MMC1和MMC3采用定功率控制,而MMC2采用定电压控制,详细的系统参数如附录B表B1所示。 本小节以分散配置方案为例进行详细的仿真分析。该方案是指将限流电感配置在直流线路两端,而换流站出口则配置固定的平波电抗器(本文取Ldc=2 mH),分散配置的优化变量可以表示为X=[L12,L21,L13,L31,L23,L32]。将4.1节设置的各个参数代入约束条件,并根据3.3节中的步骤对限流电感进行优化。为提高结果的可靠性,本文取10次优化结果的平均值,结果为X=[21,13.9,20.2,17.2,14.0,17.5]mH。附录A图A4为某一次优化过程中目标函数随迭代次数变化曲线,可见该算法具有较快的收敛速度。 为了证明仿真结果的有效性,将得到的最优值应用于测试系统,并分别设置故障F1~F6,检验优化结果是否满足系统的要求。仿真结果如表1和表2所示,其中故障Fi的上、下两行电流值分别对应故障后t1=5.17 ms(实际最大故障清除时间)和t2=7 ms(优化时的故障清除时间)的各个变量值。 表1 支路电流仿真结果Table 1 Simulation results of branch line current 表2 桥臂电流和电容电压仿真结果Table 2 Simulation results of arm currents and capacitor voltages 从表1和表2中可以看出,系统在故障后t1时刻的支路电流、桥臂电流和子模块电容电压均小于其上限值(6 kA,2.6 kA,28 kV),并具有一定的裕度,因此优化结果能够满足系统要求。同时可以看出,在t2时刻,换流站1在其线路出口故障(F1和F3)的情况下,其最大桥臂电流接近或略大于IGBT过流保护阈值2.6 kA,而其他变量距其上限值相对较远,因此换流站1受子模块过流约束影响较大;同理可以分析出,换流站2受电容最小电压约束影响较大,而换流站3则同时受到最低电压和直流断路器最大中断电流的影响。各个换流站和直流断路器受到的主要约束不同导致了CLR的配置差异。 优化之前系统采用了文献[5]中提出的限流电感计算方法,该方法主要考虑了直流断路器的约束条件,其计算结果为X=[L12,L21,L13,L31,L23,L32]=[18.5,13.7,17.1,15.8,14.2,17.9]mH。与本文的优化结果相比,L21,L23和L32相差较小,这是因为它们受到的主要约束均来自直流断路器;L12和L13则相差较多,这是因为原配置方案中没有考虑桥臂过流的约束,而L31由于没有考虑最低电压限制也导致其配置较小。因此,优化后的配置方案更加全面、准确。 限流电感除了可以配置在直流线路两端,还可以配置在换流站的出口(集中配置),或同时配置在换流站出口和直流线路末端(混合配置)。但无论采用哪种配置方案,本文提出的设计方法均有效,仅需要修改相应的决策变量即可。以集中配置方案为例,换流站出口的平波电抗器电感值Ldci变为决策变量,即学员X=[Ldc1,Ldc2,Ldc3],而直流线路末端的限流电感变为定值(可以取保护所需的最小电感值Lp,min),优化结果为Ldc1=12.4 mH,Ldc2=4.7 mH,Ldc3=10.1 mH。 从优化算法的角度而言,分散配置、集中配置和混合配置时的决策变量个数分别为2nl,nc和2nl+nc(nl为直流线路个数、nc为换流站个数),决策变量的个数越少,全局最优解也相对更精确和稳定。此外,CLR配置位置会影响系统的动态响应和CLR成本,具体采用何种配置方案需要结合实际工程来具体分析。 CLR是目前MTDC电网工程中常采用的一种限流方法,但随着系统复杂度增加和运行可靠性要求提高,CLR的参数选择也变得更加复杂。为解决这个问题,本文提出了一种通用的CLR优化设计方案,并得到主要结论如下。 1)实现了以系统配置总电感最小为目标的CLR配置方案,能够有效地减少工程中对CLR的投资成本,并减小限流电感过大给系统带来的不利影响。 2)综合考虑直流断路器、换流站闭锁和保护配置三方面的约束,保证了故障穿越期间系统的连续、可靠运行。 3)设计方案具有通用性,能够适用于不同的直流网络拓扑,由于采用了短路电流近似计算模型,大大提高了计算速度。 4)为实际工程中CLR的参数选择提供了理论依据,但在配置地点、成本分析、动态特性等方面仍需要进一步的研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。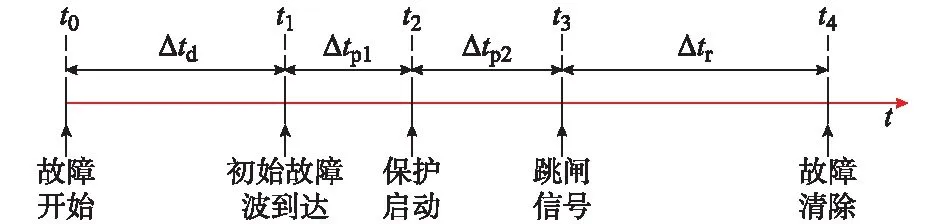
2.2 换流站闭锁


2.3 保护需求
3 CLR优化设计步骤
3.1 优化目标和约束条件
3.2 确定最严重故障场景和故障清除时间
3.3 确定CLR的全局最优值
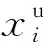
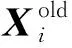
4 算例分析
4.1 测试系统和参数设置
4.2 仿真分析

4.3 其他配置方案
5 结语
