某矿坑岩质边坡稳定性数值模拟分析
2018-12-06梅世伦
梅世伦
某矿坑岩质边坡稳定性数值模拟分析
梅世伦
(贵州省公路工程集团有限公司,贵州 贵阳 550008)
为确保某矿坑周边建(构)筑物及配套工程建设的安全,采用理论分析和数值模拟的方法对矿坑区域3个典型区段岩质边坡的稳定性进行分析。根据赤平投影图中层理、裂隙以及坡面特点,初步分析3个区段岩质边坡的稳定性。采用三维有限元软件,依据现场岩质边坡节理、层理特点并考虑周边环境条件,建立各区段岩质边坡的三维数值分析模型,对相应区段边坡在自重荷载和坡顶地面荷载条件下的位移、应力状态进行数值模拟,获得矿坑各区段边坡在坡顶地面荷载作用下塑性区的分布规律。研究结果表明:数值计算获得的矿坑各区段岩质边坡的稳定性可以分为不稳定、欠稳定和稳定3个状态,与采用赤平投影分析方法获得结果具有较高的吻合性,验证了采用数值模拟分析方法分析岩质边坡稳定性的可靠性。建议对处于不稳定状态的边坡在整个区域内采用锚索进行支护处理,对处于欠稳定状态的边坡在一定范围内采用锚杆(或锚索)进行加固处理。
岩质边坡;塑性区;稳定性;赤平投影;有限元
极限平衡法、极限分析法、滑移线场法[1−4]等传统方法常用于均质土坡的稳定性分析,而在实际工程实践中最常用的是极限平衡法与数值模拟方法[5−7]。岩质边坡不同于均质的土质边坡,其岩体中含有大量诸如层面、节理、裂隙、软弱夹层、岩脉和断层破碎带等不同构造、产状和特性不连续结构面,从而给岩质边坡的稳定性分析带来了困难。郑颖人等[8]采用有限元强度折减法对岩质边坡破坏机制进行了数值模拟分析,并根据塑性力学破坏原理,验证了有限元强度折减法分析岩质边坡破坏机制的可行性。赵伟等[9]基于FLAC3D有限差分计算程序,采用强度折减法模拟分析了含有一组结构面和两组结构面的岩质边坡的稳定性,并求出了边坡的安全系数。夏开宗等[10]通过分析顺层岩质边坡中的水力作用,建立了结构面(出流缝)未被堵塞和被堵塞两种情况下顺层边坡的水力模型,得出两种情况下顺层岩质边坡稳定性安全系数。金书滨等[11]采用三维有限元软件,对某大峡谷玻璃桥桥址边坡在天然状态下和桥梁荷载条件下的位移、应力状态进行数值模拟,从坡体在玻璃桥荷载作用下塑性区的分布规律分析了边坡的稳定性。孟庆文等[12]以某高速铁路高边坡为例,分别计算了不同施工阶段滑面为圆弧面和折线面、坡体无水和饱和等各种条件下边坡的稳定性安全系数并分析了其影响规律。上述相关学者的研究表明,岩质边坡的稳定性主要由其结构面控制。本文以某矿坑岩质边坡为例,依据各区段岩质边坡的赤平投影图,初步分析相应区段岩质边坡的稳定性,并采用有限元分析软件ABAQUS,建立考虑岩体节理、层理特点的三维岩质边坡模型计算各区段边坡的稳定性,模拟岩质边坡在天然状态下和外界环境荷载条件下的位移场、应力场状态。结合赤平投影分析和数值模拟分析结果,综合评价相应区段岩质边坡的稳定性,并提出潜在失稳边坡的治理措施。
1 工程概况
某矿坑位于湖南省长沙市望城区内,为露天开采的石灰岩采石场所遗留的采石坑。矿坑周边拟修建大型儿童游乐场。矿坑顶纵向最长约为480 m,横向最长约450 m,矿坑底纵向最长约为390 m,横向最长约为380 m。
1.1 地形地貌
现矿坑岩质边坡为山体开挖后与剩余山体形成的近环形斜坡,坡度45°~90°,总体周边高、中间低,其中坑内标高约为−12.89~−16.56 m,北侧坑顶标高36~55 m,东侧坑顶标高36~53 m,西侧坑顶标高49~55.2 m,南侧坑顶标高坑顶标高43~57.0 m,最高点为场地西北侧,标高70.00 m。地形地貌特征如图1所示。

图1 某矿坑岩质边坡地形地貌特征
1.2 岩质参数
根据场地钻探揭露,矿坑岩质边坡坡体主要包含以下3种地层:
1) 人工填土(Q4ml):为杂填土,灰褐、褐黄等杂色,主要由碎石土、砼块、砖等建筑垃圾与生活垃圾混10~35%的黏性土组成,系新近堆填,稍湿,结构松散~稍密,密实度不均匀,尚未完成自重 固结。
2) 泥盆系(D)微风化灰岩:浅灰色、灰白色、灰白夹红色、深灰色,矿物成分主要为方解石、含少量白云石,隐晶~细晶质结构,中厚层状构造。裂隙稍发育,局部顶部见溶蚀粗糙面。岩石坚硬质脆,金钢石钻进一般,岩芯多呈柱状、长柱状,少量块状,岩石质量指标RQD为好的,介于82~90之间,属较硬岩,岩体较完整,岩体基本质量等级为Ⅲ级。
3) 泥盆系(D)中风化泥灰岩: 灰,深灰色,青灰等色,矿物成分主要为方解石泥晶,泥状结构,岩石坚硬质脆,金钢石钻进一般,岩芯多呈柱状、长柱状,少量块状,岩石质量指标RQD为好的,介于78~88之间,属较软岩,岩体较完整,岩体基本质量等级为Ⅳ级。
岩质边坡钻探揭露相应区域物理力学参数如表1所示。
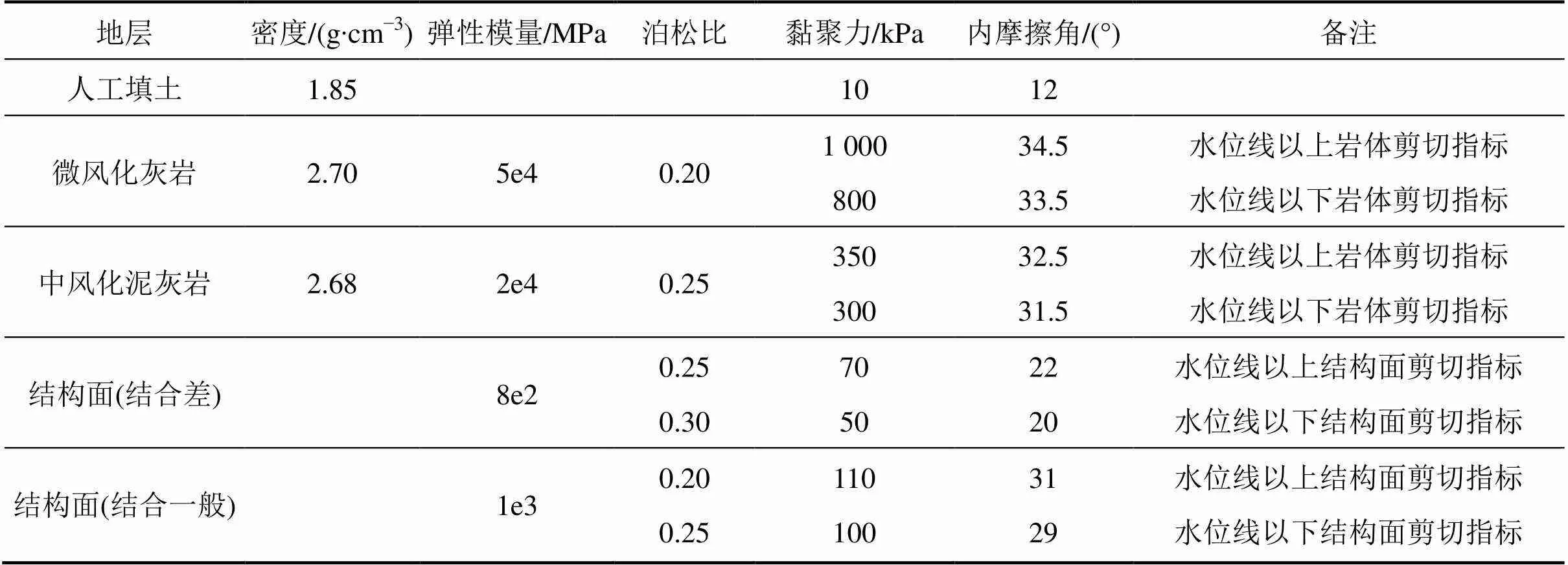
表1 矿坑地区岩质边坡物理力学参数
2 岩质边坡稳定性评价方法与理论
2.1 赤平投影分析理论
岩质边坡的稳定性受岩体结构面控制,赤平投影法能清晰的反应各结构面之间的组合及交叉关系,可初步判别边坡稳定。在构造地质学中常采用上极点下半球的投影方式进行投影[13]。
岩质边坡的滑动主要分为平面滑动和楔形体滑动。对于主要由一组结构面控制的平面滑动,其对应的岩质边坡稳定性评判标准如图2所示。对于主要由2组结构面控制的楔形体破坏,其赤平投影示意图见图3所示,通过结构面与边坡产状关系可初步判断边坡稳定性。
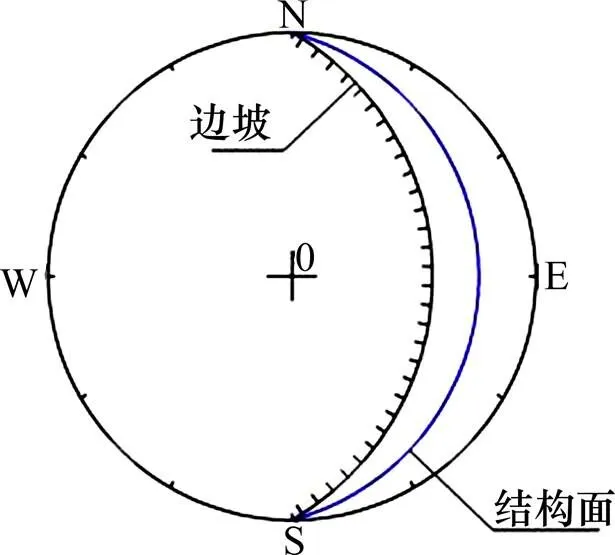
图2 1组结构面的赤平投影图

图3 2组结构面的赤平投影图
2.2 有限元分析理论
1) 本构模型的选择
根据工程实际情况,结构体采用弹塑性材料,选用Mohr-Coulomb准则。
Mohr-Coulomb模型的屈服准则为剪切破坏准则,其剪切屈服面的函数为:
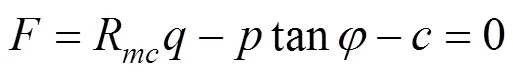
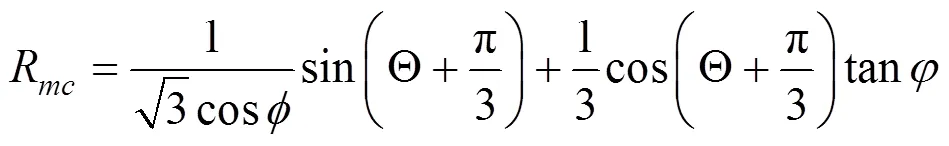
运用Mohr-Coulomb模型时需注意以下问题:
①Mohr-Coulomb模型需联合线弹性模型一并使用。
②Mohr-Coulomb采用了非关联流动法则,软件中需采用非对称求解器。
③Mohr-Coulomb模型中的黏聚力必须大于0,对于沙土等材料,可将黏聚力取一较小值。
④剪胀角的取值若与摩擦角相同,则在剪切破坏中会发生体积无限制膨胀的现象,因此需慎重选取。
2) 结构面的模拟方法
目前常采用软弱夹层或无厚度接触单元对结构面进行模拟[14]。软弱夹层模拟法是将结构面视为实体单元,与结构体一同采用Mohr-Coulomb本构关系进行理想弹塑性模拟,按照连续介质处理,通过材料参数对二者进行唯一区分,即将软弱夹层视为比结构体强度稍低的另一材料。有限元模拟如图4所示。
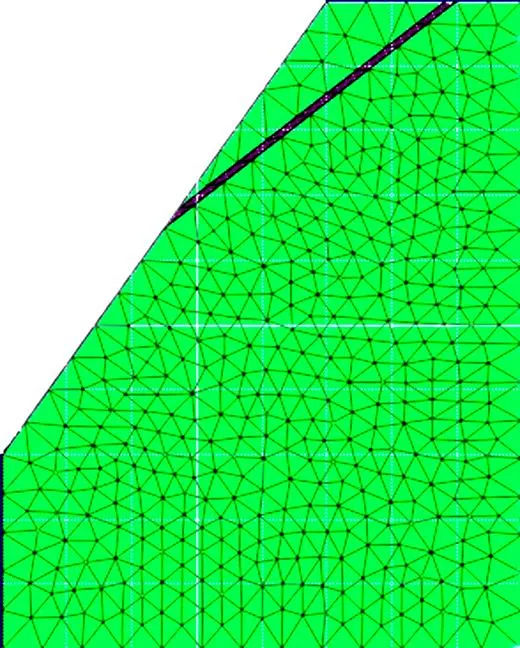
图4 软弱夹层模拟示意图
无厚度接触单元模拟法是将岩体结构面的接触面及其缝隙视为整体,利用软件中的接触单元定义接触关系。将2个接触边界平面合称为“接触对”,其中一个平面称为“目标面”,另一个平面则称为“接触面”。定义两接触面之间不产生相互的拉应力,二者可以分离(不接触),也可相对滑动。有限元模拟如图5所示。
郑颖人等[14]通过对比发现,无论是采用软弱夹层还是无厚度接触单元模拟结构面,得到的结果十分接近。也就是说,上述2种方法均可对结构面进行模拟,本文选用软弱夹层进行结构面的模拟。

图5 无厚度接触单元模拟示意图
3) 边坡失稳判据
目前岩质边坡的有限元计算失稳判据尚未统一,许多研究者对失稳判据提出了不同的建议,主要归纳为以下几类[15−16]:
①收敛性判据:以在规定的迭代次数内,力或者位移的不收敛性作为边坡整体破坏的标志。
②贯通塑性区判据:以边坡的广义塑性应变或者等效塑性应变从坡底到坡顶贯通作为边坡整体破坏的标志。
③突变性判据:以边坡坡面特征节点位移发生突变且无限发展,滑动面坡体无限移动作为边坡整体破坏的标志。
④动力学判据:以加速度是否为零作为边坡破坏的标志。
对于边坡稳定分析中的塑性应变可采用云图方式准确清晰地显示出其位置、发展状况及应变值的大小。因此,本文考虑采用塑性区的贯通情况判据进行岩质边坡失稳判断。
该矿坑岩质边坡稳定性分析时,根据现场地质测绘和钻探结果将该矿坑岩质边坡分为A,B和C等3个典型区段,分别从赤平投影分析和有限元分析2个方面综合评价各区段岩质边坡的稳定性。
3 岩质坡稳边定性分析
3.1 赤平投影分析
根据现场地质勘察资料,绘制矿坑岩质边坡3个典型区段的赤平投影图,如图6所示,各区段岩质边坡稳定性赤平投影分析结果如表2所示。

(a) A区段赤平投影图;(b) B区段赤平投影图;(c) C区段赤平投影图

表2 各区段边坡赤平投影分析一览表
注:表中L-L1表示2个结构面交线倾伏向与坡向的一致程度,通过倾向差值进行判断(同向:0°~15°,基本同向:15°~90°,反向:超过90°),鉴于坡面倾角均大于各结构面交线倾伏角,倾伏角不纳入讨论范围
利用赤平投影方法对各区段岩质边坡稳定性进行初步分析之后,结合刚体极限平衡法以两组结构面引起的楔形体滑动为对象进行理论研究[17],假定滑体为刚体,滑面遵循Mohr-Coulomb破坏准则,示意图如图7,分析如下:

图7 楔形体滑面示意图
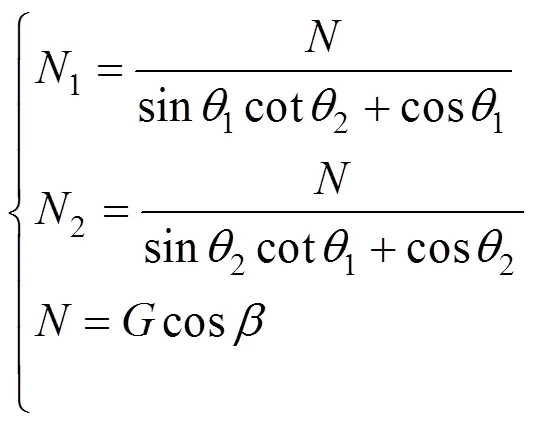
当不考虑滑动面黏聚力时,对应的下滑力F和抗滑力F分别为:

对应的稳定性系数为:

该方法从理论上解释了2组画面控制的楔形体滑动的稳定性系数方法,不足在于滑面形状过于规则化,与实际复杂情况不符,且实际情况的岩体中发育有多组结构面,2组结构面略显不足。
3.2 有限元计算分析
1)有限元三维模型的建立
依据各区段边坡剖面图,建立矿坑岩质边坡三维模型。采用软弱夹层模拟思想,将边坡岩体切割出节理、裂隙等软弱结构面,分别模拟每各个边坡的结构情况。A区段的模型如图8所示。其他区段的建模方法与A区段类似。

图8 A区段岩质边坡模型
2) 计算参数的确定
结构面、结构体均采用实体单元模拟,相关力学参数参见表1。坡顶荷载值按后期工程设计概况实际情况施加。模型所受荷载有重力以及运营阶段的建筑物基底正向荷载,基底正向荷载根据游乐设施单体荷载估算,取100 kN/m2,作用于边坡顶部,并考虑了在现有矿坑内水位的影响时水上、水下结构体参数的不同。
3) 计算结果分析
使用塑性区贯通判据进行各区段岩质边坡稳定性评判。图9~14分别为A,B和C区段塑性区及竖向位移的分布情况。
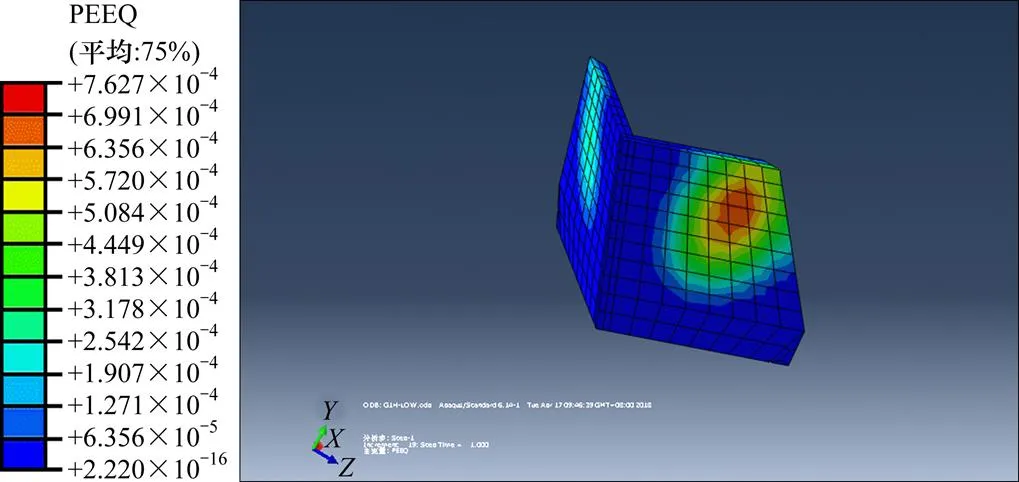
图9 外荷载作用下A区段塑性区分布
从图9中可以看出,在外荷载作用下,A区段楔形体塑性区发展较为明显,但未形成连续的、贯通的区域,由位移分布图(见图10)可以看出,楔形体上方岩体发生了轻微变形,顶部位移最大,为8.591 mm,坡底区域有十分微小的反向位移,存在上拱的趋势,以塑性区发展情况为主要依据判断该边坡欠稳定。各边坡最大位移值、塑性区情况及稳定性判断见表3。
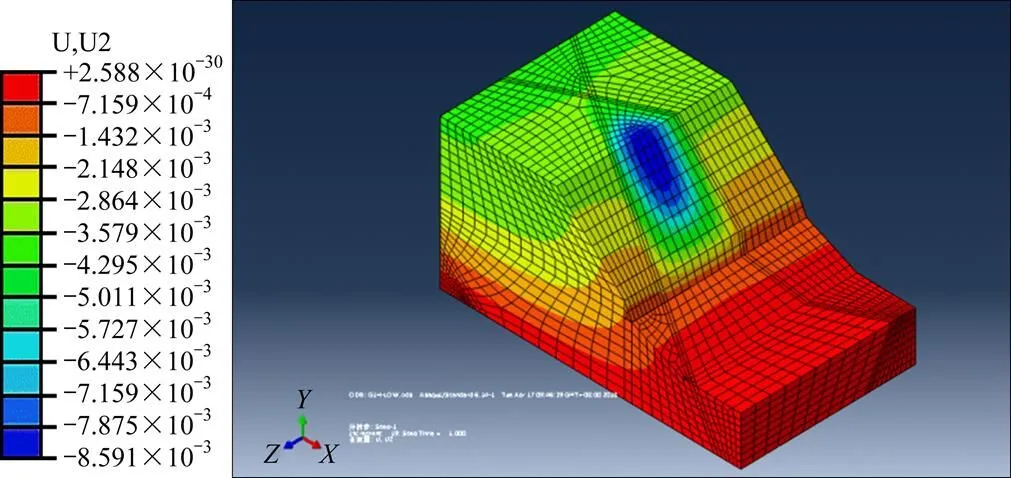
图10 外荷载作用下A区段竖向位移云图
从图11中可以看到,在外荷载的作用下,B区段边坡岩体塑性区由下至上发展、贯通,由位移分布图(见图12)可以看出,该平面形结构面岩质边坡的岩体下部位移较小,上部位移较大,等位移线呈弧形分布,坡顶最大位移达到22.20 mm,表明结构面上部岩体发生滑塌的概率较大,边坡主要沿平面形结构面发生滑移破坏,综合判断B区段为不稳定边坡。
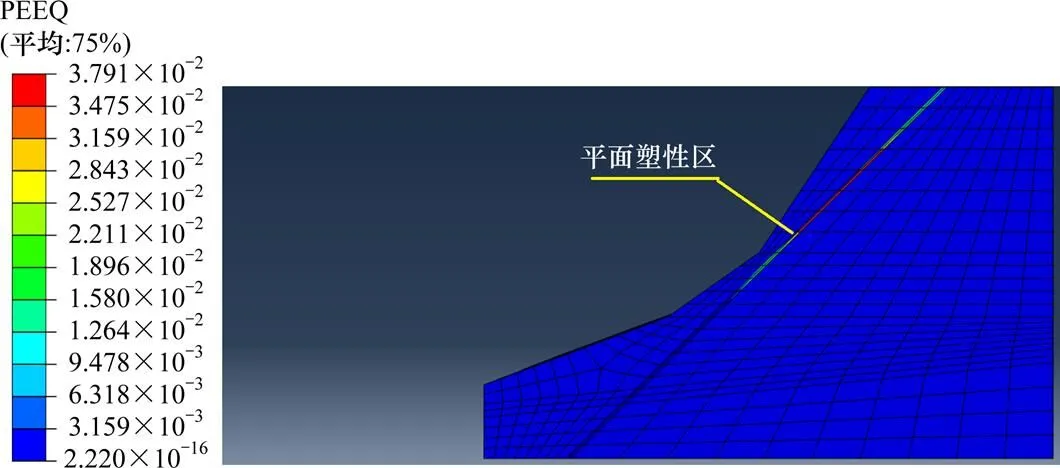
图11 外荷载作用下B区段塑性区分布
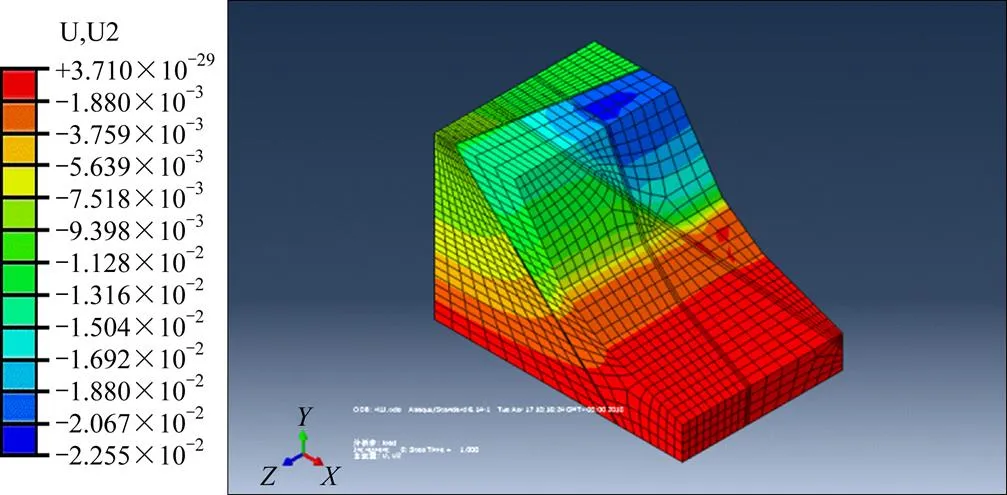
图12 外荷载作用下B区段竖向位移云图

图13 外荷载作用下C区段塑性区分布
从图13中可以看出,在外荷载作用下,C区段平面形结构面塑性区发展不明显,仅底部一小段。由位移分布图(见图14)可以看出,坡体顶部位移最大,为5.578 mm,根据塑性区发展情况并结合位移量判断C区段岩质边坡处于稳定状态。

图14 外荷载作用下C区段竖向位移云图

表3 各区段边岩质边坡稳定性有限元分析
4 结论
1) 采用赤平投影理论初步分析了3个典型区段岩质边坡的稳定性。
2) 依据现场岩质边坡节理、层理特点并考虑周边环境条件,建立了岩质边坡三维有限元模型,分析了各区段边坡在外荷载条件下的塑性区分布情况、位移分布特点。
3) 根据数值模拟分析结果,所计算矿坑各区段岩质边坡的稳定性可以分为不稳定、欠稳定和基本稳定3个状态,建议对处于不稳定状态的边坡在整个区域内采用锚索进行支护处理,对处于欠稳定状态的边坡在一定范围内采用锚杆(或锚索)进行加固处理。
[1] Kim j, Salgado R, Lee J. Stability analysis of complex soil slopes using limit analysis[J]. Journal of Engineering, ASCE, 2002, 128(7):546−557.
[2] 郭子仪, 范振华. 边坡稳定性分析中的有限元极限平衡法[J]. 武汉理工大学学报, 2014, 1(38): 79−84. GUO Ziyi, FAN Zhenhua. Finite element limit equilibrium method for slope stability analysis[J]. Journal of Wuhan University of Technology, 2004, 1(38): 79−84.
[3] Manzari M T, Nour M A. Significance of soil dilatancy in slope stability analysis[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2000, 126(1): 75−80.
[4] LIU Y Q, LI H B, DAI H C. Preliminary study on the progressive failure of a layered rock slope under explosions[J]. Key Engineering Materials, 2006, 36(8): 1461−1466.
[5] CHENG Y M, Lansivaara T, WEI W B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods[J]. Computers and Geotechnics, 2007, 34(3): 137−150.
[6] Stianson J R, Fredlund D G, Chan D. Three-dimensional slope stability based on stresses from a stress-deformation analysis[J]. Canadian Geotechnical Journal, 2011, 48(6): 891−904.
[7] 沈华章, 郭明伟. 基于离散元的边坡矢量和稳定性分析方法研究[J]. 岩土力学, 2016, 37(2): 592−600. SHEN Huazhang, GUO Mingwei. Vector sum method for slope stability analysis based on discrete elements[J]. Rock and Soil Mechanics, 2016, 37(2): 592−600.
[8] 郑颖人, 赵尚毅, 邓卫东. 岩质边坡破坏机制有限元数值模拟分析[J]. 岩石力学与工程学报, 2003, 22(12): 1943−1952. ZHENG Yingren, ZHAO Shangyi, DENG Weidong. Numerical simulation on failure mechanism of rock slope by strength reduction fem[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 1943−1952.
[9] 赵伟, 李自杨. 岩质边坡稳定性有限差分强度折减法分析[J]. 四川地质学报, 2016, 36(4): 613−615. ZHAO Wei, LI Ziyang. Analysis of slope stability based on finite difference and strength reduction method[J]. Sichuan Geological Journal, 2016, 36(4): 613−615.
[10] 夏开宗, 陈从新, 鲁祖德, 等. 考虑水力作用的顺层岩质边坡稳定性图解分析[J]. 岩土力学, 2014, 35(10): 2985−2994. XIA Kaizong, CHEN Congxin, LU Zude, et al. Analysis of stability diagram of rock bedded slope under hydraulic pressure[J]. Roil and Soil Mechanics, 2014, 35(10): 2985−2994.
[11] 金书滨, 胡涛, 乔世范. 某大峡谷玻璃桥桥址边坡稳定性分析[J]. 铁道科学与工程学报, 2016, 13(11): 2197− 2203. JIN Shubin, HU Tao, QIAO Shifan. The stability analysis of the slope of glass bridge site in a grand canyon[J]. Journal of Railway Science and Engineering, 2016, 13(11): 2197−2203.
[12] 孟庆文, 冷伍明. 山区高速铁路高陡边坡稳定性与变形分析[J]. 铁道科学与工程学报, 2012, 9(6): 55−59. MENG Qingwen, LENG Wuming. Research of stability and deformation on the high and steep slope of high speed railway in mountainous regions[J]. Journal of Railway Science and Engineering, 2012, 9(6): 55−59.
[13] 徐开礼, 朱志澄. 构造地质学[M]. 2版附本. 北京: 地质出版社, 2006. XU Kaili, ZHU Zhicheng. Structural geology[M]. second edition attached. Beijing: Geological Press, 2006.
[14] 郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡中的应用[M]. 北京: 人民交通出版社, 2011. ZHENG Yingren, ZHAO Shangyi, LI Anhong, et al. Finite element limit analysis method and its application in slope[M]. Beijing: China Communications Press, 2011.
[15] 张晓咏, 戴自航. 应用ABAQUS程序进行节理岩质边坡稳定分析[J]. 广西大学学报(自然科学版), 2009(4): 444−450. ZHANG Xiaotong, DAI Zihang. Stability analysis of jointed rock slopes using ABAQUS program[J]. Journal of Guangxi University, 2009(4): 444−450.
[16] 靳付成. 岩质边坡失稳判据及临界滑动面确定方法研究[D]. 南京: 河海大学, 2007. JIN Fucheng. Research on the criterion of rock slope instability and the determination of critical slip surface[D]. Nanjing: Hehai University, 2007.
[17] 韩颖. 岩质边坡楔形体稳定分析[D]. 杭州: 浙江大学出版社, 2006. HAN Ying. Stability analysis of rock slope wedges[D]. Hangzhou: Zhejiang University Press, 2006.
The numerical simulation analysis of rock slope stability in a pit
MEI Shilun
(Guizhou Highway Engineering Group Co., Ltd., Guiyang 550008, China)
In order to ensure the safety of the engineering constructionaround a pit, the theoretical analysis and numerical simulation methods were used to analyze the stability of rock slopes in the three typical sections of the pit area. The stability of rock slopes in three sections was analyzed based on the features of bedding, cracks, and slopes of the stereographic projection. A three-dimensional finite element software was used to establish a three-dimensional numerical analysis model for rock slopes in each section, considering the surrounding environmental conditions and based on the joints and bedding features of rock slopes in the site. The displacement and stress state of each section slope under adjacent building load and gravity load were numerically simulated to obtain the distribution law of the plastic zone. The results show that the stability of rock slopes in each section of the pit can be divided into three states: unstable, lack of stable, and stable. This agrees well with the results obtained using the stereographic projection analysis method, which verifies the reliability of using numerical simulation method to analysis of rock slope stability. Several suggestion is recommended that the slopes in the unstable state be supported with anchor cables in the entire area, and the slopes lack of stable should be reinforced with anchor rods (or anchor cables) within a certain range.
rock slope; plastic zone; stability; stereographic projection; finite element
10.19713/j.cnki.43−1423/u.2018.11.013
TU47
A
1672 − 7029(2018)11 − 2825 − 08
2017−11−01
长沙理工大学交通基础设施安全风险管理行业重点试验室开放基金资助项目(16KE03)
梅世伦(1979−),男,贵州安顺人,高级工程师,从事公路工程施工技术与管理工作;E−mail:64317678@qq.com
(编辑 涂鹏)
