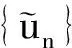一类非线性基尔霍夫方程约束极小值点的存在性

袁志宏

(吕梁学院 数学系,山西 吕梁 033001)

0 引言

考虑下列Kirchhoff型问题

(1)

其中a,b>0为常数,.

问题(1)中,当λ=0且|u|p-2u和RN分别用f(x,u)和有界区域Ω⊂R4代替时,转化为基尔霍夫问题Dirichlet问题

这一问题最早可参考文献[1]以及相关文献.

近年来,国内外学者对Kirchhoff型方程进行了广泛的研究并取得丰富的成果,其中对于问题(1),当p∈(2,2*)且λ是一个数或一个位势函数时,已得到解的存在性结论;另外,当p∈(2,4)时,Li和Ye在文[2]中考虑了λ=-1的情形,并利用Nehari和Pohozaev不等式,得到在R3上至少有一个能量解的结论.最近文[3]讨论了N≤3,P∈(2,2*)时,问题(1)的约束极小点的存在性.受此启发,这里讨论N=4,P∈(2,3),问题(1)的可解性.

1 准备工作和主要结论

则问题(1)的约束基态解可转化为求泛函I在Ic的临界点,即对任意给定的c>0,若uc是I|Sc上的临界点,λc为相应的Lagrange乘数,则称(uc,λc)为问题的解.

引理1[9](Gagliardo-Nirenberg不等式)若p∈(2,2*),N≥3,则

方便起见,我们记

则I(u)=A(u)+B(u)-C(u).且对任意的u∈Sc,由引理1可得

(2)

(3)

下面给出主要结论.

定理 若20.

2 主要结论的证明

引理2 若2

因20,则ut∈Sc,且当t→∞时

Ic2≤I(ut)=t2A(u)+t4B(u)-t2(p-2)C(u)→0.

即对任意的c>0,有Ic2<0.

2)设{un}⊂Sc为Ic2的极小化序列,则存在与n无关的正数k1,k2(k1

(4)

(5)

联立(4)(5),Ic2

注 由上述定理可知,{c∈(0,+∞)|Ic2<0}≠ø,不妨设c*=inf{c∈(0,+∞)|Ic2<0},显然,c*=0.

引理3 若2

证明 因(I|Sc)′(u)=0,则存在λc∈R使得I′(u)-λcu=0,方程两边同时匹配u有

2A(u)+4B(u)-pC(u)=λcc2.

(6)

另一方面,根据Pohozaev不等式[6]

2A(u)+4B(u)-4C(u)=2λcc2,

(7)

下面给出定理的证明.

对20,设{un}⊂Sc为Ic2的极小化序列,由引理2知,Ic2<0且对任意的n∈N+,有

(8)

其中当n→+∞时∘(1)→0.结合Brezis-Lieb引理,h:c→Ic2的连续性以及(8)有