学生作弊问题的演化博弈分析
2018-12-06张莉,党红
张 莉,党 红
(长治学院 数学系,山西 长治 046011)
0 引言
考试是检验考生知识水平和教师教学能力的最基本、最主要的途径之一,为了保证结果的公平, 考场上必须要求考生严格遵守考试纪律. 近年来, 高校考试中考生作弊现象屡见不鲜, 考试出现诚信危机[1]. 针对这一现象, 许多高校在考试前与考生签订“诚信考试承诺书”, 然而往往收效甚微, 许多考生并未将此当回事. 此外, 由于监考教师在监考过程中有时出于同情心理, 不想考生因被举报作弊而受到诸如重修、记过、取消学位证等处罚, 在发现考生作弊时不及时向学校举报, 而只是没收其作弊工具, 对其进行口头警告等, 致使考生抓住监考教师这一心理特点, 有恃无恐. 因此, 解决高校考生考试作弊问题刻不容缓.
近年来,很多学者对于考生作弊现象进行了研究,其中也有些学者应用博弈论的相关知识对考生作弊现象进行研究与分析,但是,大部分的学者都是基于考生是完全理性人这一前提.例如:程香丽、张福磊[2]研究考生之间的囚徒困境博弈, 进而揭示影响考生作弊行为及监考教师处理作弊行为的主要因素; 王美荣[3]运用理性人假设和博弈论的有关原理对考试作弊行为及其互相影响进行深入剖析, 探讨作弊行为的成因与制约因素, 并提出了针对性的治理建议; 张秀英[4]从经济博弈的角度分析了考试作弊行为, 通过对模型的建立和推导得出一个混合策略纳什均衡, 并通过对策略空间的分析, 提出一些控制和减少这种行为的合理建议. 这些都是在考生具有完全理性的前提下进行的研究, 也就是说考生能够判断怎样做选择能够达到自身的最大利益. 但是往往在现实生活中, 考生基于侥幸心理或其他原因, 总是通过不断的试错才会最终达到一个稳定的策略, 也就是说考生是有限理性的.
本文运用演化博弈理论, 认为博弈双方是有限理性的局中人, 构建考生与监考教师之间的演化博弈模型, 得出并分析双方主体的复制动态方程, 找出学生作弊现象存在的主要原因, 为学校监管和控制学生作弊现象提供参考.
1 基于博弈论的学生作弊问题分析
1.1 理论基础
演化博弈论是经典博弈论与演化理论的有机结合[5]. 经典博弈论认为参与人是完全理性的, 以追求自身最大利益为目标, 即要求参与人在博弈时能够选择最大化自身利益的策略. 而演化博弈论放弃完全理性的假设, 从有限理性的角度分析人类经济活动, 认为参与人只拥有有限的知识和判断推理能力, 双方并不会一开始就找到最优策略, 也并不具有最优行为, 各主体的最优行为是通过不断模仿, 反复学习等动态变化过程来实现的[6-9].
1.2 模型的建立
本文以考生与监考教师为主体, 在两者的利益过程中建立演化博弈模型.
模型假设:
1)博弈双方都是有限理性的局中人.
2)假设考生在考试过程中可采取作弊A和不作弊B两个策略; 监考教师可采取举报C和不举报D两个策略, 即考生的策略集为{A,B}, 监考教师的策略集为{C,D}.

表1 考生监考教师收益矩阵
3)假设r为考生作弊的收益(考生作弊带来的成绩的提高和逃避复习减少的精力投入);g为考生因作弊被监考教师举报所受到的处罚(例如: 重修、记过、取消学位证等);m为考生正常考试的收益(考生真实的成绩和对知识的掌握程度);t为监考教师的揭发举报成本(教师投入考试的精力等);n为教师发现作弊不举报受到的来自学校的处罚. 因此, 考生与监考教师之间的收益矩阵如表1所示.
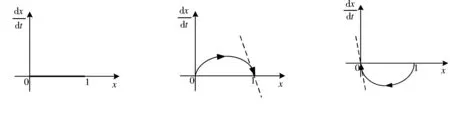
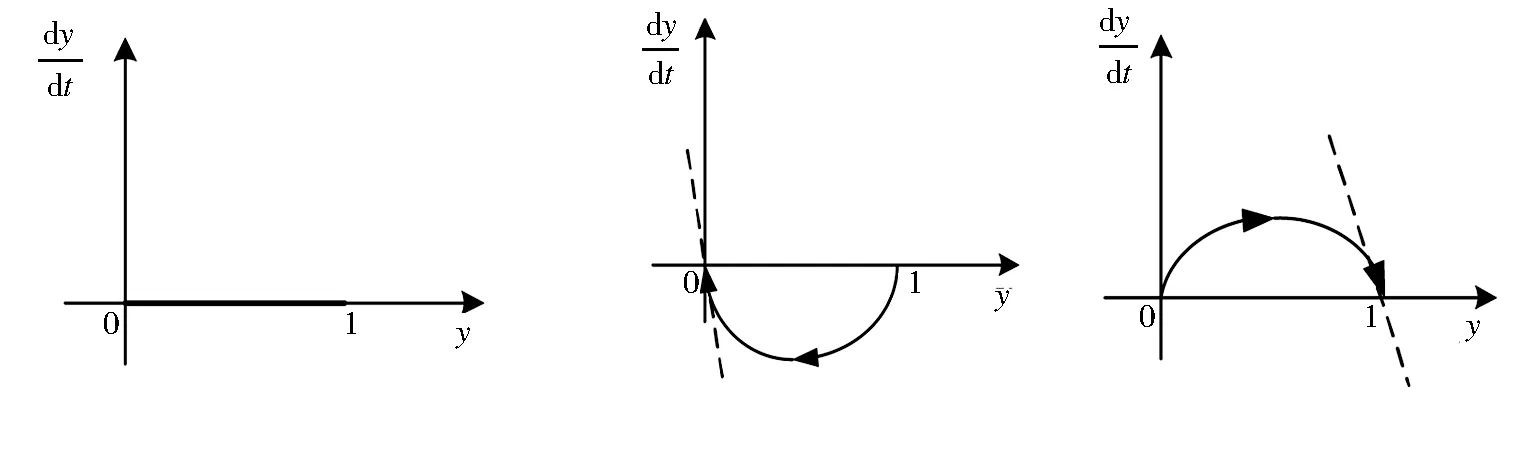
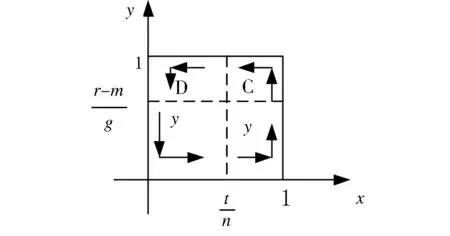
其中考生作弊的收益r理应大于不作弊的收益m,而应小于作弊被举报时所受的处罚g,即m 则:UA=y(r-g)+(1-y)r=r-gy UB=ym+(1-y)m=m 则:UC=x·(-t)+(1-x)·(-t)=-t UD=x·(-n)+(1-x)·0=-nx 考生群体的复制动态方程为: 由复制动态方程和演化稳定策略的性质可分以下几种情况: 总结以上情况, 考生群体的复制动态相位图如图1所示: 为为x*=0图1 考生群体复制动态相位图 监考教师群体的复制动态方程为: 由复制动态方程和演化稳定策略的性质可分以下几种情况: 总结以上情况, 监考教师群体的复制动态相位图如图2所示. 为为y*=0图2 监考教师群体复制动态相位图 图3 考生群体与监考教师群体复制动态相位图 考生群体与监考教师群体演化博弈动态复制相位图如图3所示. 由图3可知, 1)当初始状态落在A区域时, 学生作弊率、监考教师的举报率均低, 博弈收敛于平衡点(1,0), 即双方的选择为(作弊,不举报).2)当初始状态落在B区域时, 学生的作弊率高、监考教师的举报率低, 博弈收敛于均衡点(1,1), 即双方的选择为(作弊,举报).3)当初始状态落在C区域时, 学生的作弊率高、监考教师的举报率高, 博弈收敛于均衡点(0,1), 即双方的选择为(不作弊,举报).4)当初始状态落在D区域时, 学生的作弊率低、监考教师的举报率高, 博弈收敛于均衡点(0,0), 即双方的选择为(不作弊,不举报). 以上均衡点均是鞍点, 没有演化稳定策略. 本文建立了监考教师群体与考生群体的演化博弈模型, 通过分析, 可得以下结论. 1) 该模型没有演化稳定策略, 说明监考教师群体与考生群体在博弈过程中出现往复循环的行为模式.即“监考教师举报力度不够——学生作弊现象加重——监考教师加大举报力度——学生作弊现象减少——监考教师举报力度下降——学生作弊现象加重”. 这也是高校作弊问题不能根除的一个重要原因. 2) 建议: 通过分析, 学校应采取的措施为降低考生在作弊时获得的收益;增大对考生作弊的处罚, 以有效减少学生的作弊行为. 另外, 增大对监考教师发现作弊而不举报的处罚, 最终所有教师都会坚持严格监考. 双管齐下, 才能更好地治理高校学生作弊现象. 本文通过建立监考教师群体与考生群体的演化博弈模型, 分析了r(考生作弊的收益)、g(考生作弊所受到的处罚)、m(考生正常考试的收益)、t(监考教师的举报成本)、n(教师不举报受到的处罚)这些因素对监考教师与考生行为演化的影响, 提出了如何有效改善考生作弊现象的建议, 为高校学生管理提供帮助.
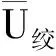
1.3 演化博弈行为分析
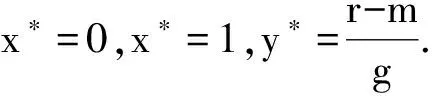
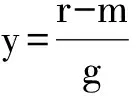
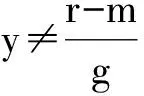
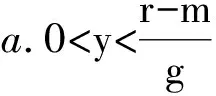
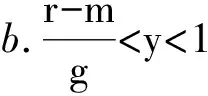
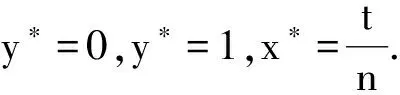

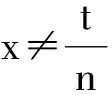
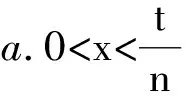

1.4 演化博弈结果分析
2 结语
