星间相对测量自主导航的改进容积卡尔曼滤波
2018-12-06张艾,李勇
张 艾,李 勇
(中国空间技术研究院钱学森空间技术实验室,北京 100094)
0 引 言
随着高分辨率对地观测、深空探测、空间在轨服务以及一系列商业航天活动的蓬勃开展,以分布式卫星系统为代表的多航天器协同工作模式已成为空间技术发展的新趋势。分布式卫星系统实现自主协同运行需要具备的核心和基础能力是自主导航,即可以不依赖地面测控站及全球导航星座系统的支持,仅利用各个卫星自备的测量设备实时确定各自的位置和速度[1]。近年来,基于星间相对测量的自主导航技术受到广泛关注,测量量包括相对距离、视线角和相对位置矢量等[2-6]。
文献[7]首先提出了不需要地面信息,仅利用星间相对位置矢量测量的双星定轨方法,并指出这种方法不适用于两卫星运行在共面圆轨道且半长轴相等的情况,但未对此方法给出严格的理论证明。文献[8]从物理角度对上述方法进行了解释,将两卫星视为一个巨型加速度计,通过协方差分析对定位误差进行研究。文献[9]对该自主导航方法从非线性系统能观性角度进行理论分析,通过数学证明,给出系统可观测的充分条件,即两卫星瞬时地心距不相等。文献[1]在上述研究基础上提出非线性系统局部k阶能观性的概念,并给出该自主导航系统局部4-6阶能观的充要条件。文献[10]考虑能观性强弱对滤波算法的影响,给出了一个基于相对位置矢量测量的自主导航系统能观性秩条件可观度评价标准,并据此对UKF算法进行改进,提高了导航定位的精度。但在该算法中,评价标准只能基于位置、速度估计值而非其真值得到,不能真实反映系统能观度大小。
卫星导航系统是一个典型非线性系统,一般采用扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法进行估计[11-17]。EKF算法采用线性化方法近似非线性函数,当系统非线性程度较强时估计效果不佳。20世纪90年代以来,多种非线性滤波算法例如无迹卡尔曼滤波(Unscented Kalman Filter, UKF)算法[18],粒子滤波(Particle Filtering, PF)算法[19]等纷纷涌现。UKF算法适用于非线性程度较强的系统,估计精度高于EKF,但在星间测量自主导航这类高维非线性系统的滤波过程中可能出现协方差非正定,导致滤波数值不稳定且有可能发散[20]。PF算法基于随机采样点进行估计,选取的粒子数越多估计精度越高,但计算量也随之大量增加,不利于在线估计。2009年Arasaratnam等人提出了容积卡尔曼滤波(Cubature Kalman Filter,CKF)算法[21],由于其设计简洁,数学理论严密,估计性能好,一经提出便受到众多学者关注[22-24]。CKF在高维非线性系统中能有效避免出现UKF的滤波发散现象和PF计算量大的问题,适用于星间测量自主导航系统。文献[25]对UKF算法和CKF算法进行了比较,指出当系统状态维数大于3维时,CKF算法的估计精度和数值稳定性都优于UKF。但是CKF算法对非线性系统估计时舍去了部分近似化误差,会造成滤波不满足拟一致性[26],从而无法对状态真值进行准确估计。文献[27-28]针对系统模型参数不准确或噪声统计特性未知的情况,提出自适应CKF算法和自适应强跟踪CKF算法,并在目标跟踪系统中验证了其有效性,但不适用于系统可观性较差的情况。由于不满足拟一致性且在可观性较差的区段估计性能较差,CKF算法应用于星间测量自主导航系统时仍需进行在线修正和改进以提高性能。
本文在上述研究的基础上,针对基于星间相对位置矢量观测的分布式卫星自主导航系统,提出一种改进容积卡尔曼滤波算法。算法基于系统可观度大小对滤波增益阵进行在线调整,使系统在可观性较差的区段滤波精度得到提升,同时满足拟一致性[29],从而能够通过在线估计给出实时导航精度范围。数学仿真表明该算法具有较高的精度和较快的趋稳速度。
1 系统模型
本文考虑的卫星系统由两颗能够进行相对观测的卫星A和B组成,测量关系如图1所示。
用下标或上标A和B分别表示卫星A和卫星B对应的量,O是地球质心,rA和rB分别是地心到两卫星的矢量,rAB是卫星A到卫星B的位置矢量。已知卫星A搭载了星敏感器和无线电测距仪,可以测量自身在惯性空间中的姿态,以及AB间的相对距离和B星在A星本体坐标系中的方位角,通过坐标转换可以得到两卫星在惯性空间中的相对位置矢量。该导航系统的目标是在仅有星间位置矢量测量的条件下,实时确定卫星A和卫星B在惯性空间中的位置和速度。

图1 星间相对位置矢量测量示意图Fig.1 Relative position vector measurement between satellites
选取地心赤道惯性坐标系,坐标原点为地球质心,基准面为赤道面,X轴指向春分点,Z轴指向北极,Y轴与X轴和Z轴构成右手直角坐标系。考虑J2摄动力作用下单个卫星的轨道动力学方程[30]
(1)


(2)

卫星的位置速度矢量与轨道动力学方程直接对应,一般选取两个卫星的位置和速度矢量作为双星系统的状态变量,即
X为12维状态变量。二体轨道下的系统状态方程可以简化为
(3)
式中:

系统观测量为惯性系下两卫星的相对位置矢量,观测方程为
Y=h(X)+v=rA-rB+v=HX+v
(4)

2 容积卡尔曼滤波
2.1 三阶球面-径向积分规则[21]
在n维实数空间Rn中,考虑如下向量函数积分
(5)



已知式(5)可以通过积分变换转化为
式中:x=ry,r=|x|,y为单位矢量,Un为n维单位球面,σ(·)为Un上的元素。应用球面容积规则和一阶高斯-拉盖尔积分规则,选取容积点为单位球面与各坐标轴的交点,即点集{1},得到式(5)的近似积分
(6)


通过以上步骤得到了非线性高斯滤波积分公式的一种近似。
2.2 容积卡尔曼滤波算法步骤
考虑如下所示的离散非线性高斯系统:

(7)

CKF的具体步骤为:
1)时间更新
①假设在k-1时刻,后验概率密度是已知的,做矩阵的平方根分解:
(8)
②计算容积点集(i=1,2,…,2n):
(9)
式(9)中由下式确定
(10)
式中:{1}i表示全对称容积点集{1}中的第i个点。
③计算传导容积点集(i=1,2,…,2n):
(11)
④估计状态向量的一步预测值:
(12)
⑤估计误差协方差一步预测值:
(13)
2)量测更新
①做矩阵的平方根分解:
(14)
②计算容积点集(i=1,2,…,2n):
(15)
式中:ξi由式(10)给出。
③计算传导容积点集(i=1,2,…,2n):
Zi,k|k-1=h(Xi,k|k-1)
(16)
④估计测量的一步预测值:
(17)
⑤估计新息协方差矩阵:
(18)
⑥估计交叉协方差矩阵的一步预测值:
(19)
⑦估计卡尔曼增益矩阵:
(20)
⑧估计当前时刻的状态向量:
(21)
⑨估计当前时刻的误差协方差矩阵:
(22)
3 基于可观度的改进容积卡尔曼滤波
CKF是非线性高斯滤波递推算法的一种近似方法,依据最小方差理论推导而来。然而与EKF、UKF一样,CKF是次优估计,在近似过程中存在误差,不能严格保证估计结果的无偏性;算法中计算出的均方误差阵PCKF与估计结果的实际均方误差阵Pture之间不存在确定的大小关系。由于在实际系统中,估计误差的真值无法得到,希望得到一种改进的容积卡尔曼滤波算法,使PCKF能够给出Pture的一个上界,即具有拟一致性[24]。拟一致算法计算得到的均方误差阵大于或等于实际的均方误差阵,便于对误差真值进行准确估计。
可观度是可观性的度量,表征系统状态可由输出反映的程度。在非线性系统中,系统的可观度大小不是固定的,会随着状态变化而改变,从而对滤波算法的估计精度产生一定影响。可观度较大的时刻,系统由观测反推状态的能力较强,估计误差较小;反之,可观度较小的时刻,由观测反推状态的能力较弱,估计误差较大。
目前常用的可观度评价准则有基于可观性矩阵的评价准则和基于滤波误差协方差阵P的评价准则。基于可观性矩阵的评价准则需要计算可观性矩阵的奇异值,求解繁琐,要基于状态真值进行计算,不具备实际操作性,只能作为离线分析参考;基于滤波误差协方差阵P的评价准则不需额外求解可观性矩阵,计算量小,但是在非线性滤波中,P阵不能代表真实的估计误差协方差,所以此准则不能真实反映系统可观度的情况。
从可观度的物理意义出发,基于滤波算法量测更新过程给出非线性系统可观度的另外一种表征方式。

(23)

矩阵的Frobenius范数定义为:若A=(aij)∈Rm×n
规定
(24)
已知Frobenius范数具有如下性质:
式中:λi(ATA)为矩阵ATA的第i个特征值。

依据以上分析,在滤波的时间更新过程中对一步预测估计误差协方差阵的计算公式进行修改,引入一个缩放参数ρ,将(13)式改写为
(25)
式中:缩放参数ρ定义如下:

γ为大于0的常数。

由此,依据当前时刻系统可观度大小对误差协方差阵进行修正,在适当扩大PCKF的基础上兼顾可观度影响,克服了CKF的PCKF阵无法反映真实误差协方差的弊端,减小了系统可观度较低区段的估计误差,使滤波更加平稳,提高了滤波精度。由式(8)~式(12),式(25),式(14)~(22)构成的算法本文称之为改进的容积卡尔曼滤波算法(Modified Cubature Kalman Filter, MCKF)。
4 仿真结果
基于前面给出的系统模型,选择一个低轨近距离双星编队,初始轨道根数如表1所示。将初始轨道根数转化为地心赤道惯性系下的位置速度向量,如表2所示。
定义两卫星相对距离为rAB=|rAB|,以表2的初始条件带入式(1)的动力学模型进行仿真,得到两卫星3个轨道周期内的相对距离如图2所示。可以看出,两个卫星的相对距离介于35 km和70 km之间。由于卫星B的偏心率非零,所以两星瞬时地心距在一个轨道周期内有两个时刻相等。基于文献[1]和[9]中结果,在这两个时刻及其邻域中系统的可观性较弱。
假设卫星A搭载了星敏感器和无线电测距仪,可以获得A在惯性空间中姿态,同时可以测量AB间距和B星在A星本体坐标系下的方位角,则相对位置矢量在惯性空间中的坐标可由式(26)解得。

表1 两卫星初始轨道根数Table 1 Initial orbital parameters of two satellites

表2 初始状态向量Table 2 Initial state vectors

图2 两星相对距离Fig.2 Distance between two satellites
(26)

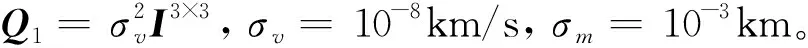
设定初始位置误差为100 km,初始速度误差为10 m/s。采用蒙特卡洛(Monte Carlo)方法对以上自主导航系统进行500次独立仿真,分别用CKF算法和MCKF算法对两卫星在惯性空间中的位置和速度进行估计,并对估计结果进行比对。


图3 CKF的位置速度滤波结果(卫星A)Fig.3 RMS errors of position and velocity using CKF(satA)

图4 CKF的位置速度滤波结果(卫星B)Fig.4 RMS errors of position and velocity using CKF(satB)

进一步,对相同初始条件下CKF和MCKF的仿真结果进行横向比较,卫星A的结果如图7所示,卫星B的结果如图8所示,图中实线表示CKF滤波结果,虚线表示MCKF滤波结果。可以看出,MCKF在1000 s左右趋于稳定,而CKF需要1800 s左右,MCKF比CKF收敛速度更快。
定义位置和速度估计误差分别为

图5 MCKF的位置速度滤波结果(卫星A)Fig.5 RMS errors of position and velocity using MCKF(sat A)

图6 MCKF的位置速度滤波结果(卫星B)Fig.6 RMS errors of position and velocity using MCKF(sat B)

图7 MCKF和CKF的滤波结果对比(卫星A)Fig.7 comparison of RMS errors between MCKF and CKF(sat A)
定义滤波精度为到达稳态后,位置速度估计误差的均值加上其三倍均方根(3σ)。将两种算法下的滤波精度进行对比,如表3所示。不难看出,MCKF的滤波精度高于CKF。
5 结 论
在分布式卫星技术背景下,研究仅利用星间相对位置测量的自主导航滤波问题。针对CKF算法的不足,提出一种MCKF算法,选择系统可观度作为标准对CKF算法的一步预测协方差阵进行修正,对可观度变化且部分时刻可观性较差的系统估计性能良好,具有拟一致性。针对低轨近距离双星任务系统开展数学仿真,相同条件下的滤波结果表明MCKF算法明显优于CKF算法,其收敛速度更快,精度更高。此外,该算法具有很好的移植性和普适性,无需修改即可适用于一般非线性系统。进一步的研究工作为MCKF算法的参数选择与稳定性的关联分析。
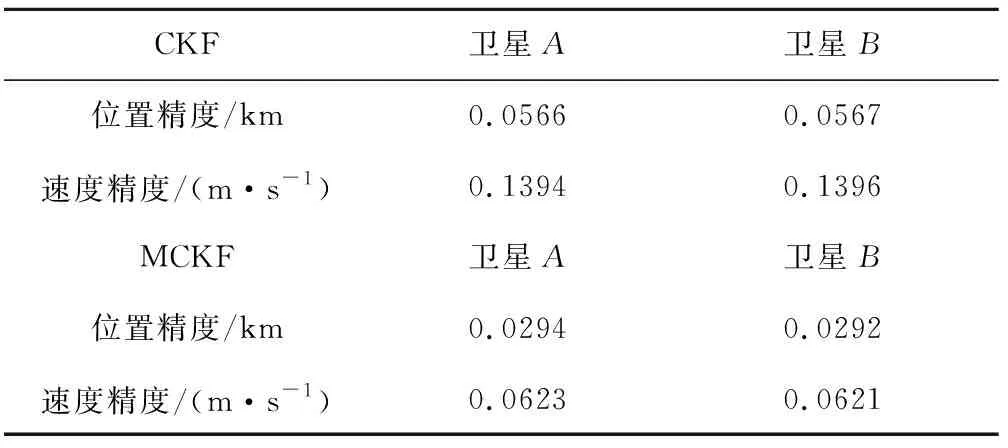
表3 MCFK和CKF滤波精度对比Table 3 Accuracy of MCKF and CKF

图8 MCKF和CKF的滤波结果对比(卫星B)Fig.8 Comparison of RMS errors between MCKF and CKF(sat B)
