有向拓扑下无径向速度测量的多导弹协同制导

吕 腾，李传江，郭延宁，吕跃勇

(哈尔滨工业大学控制科学与工程系，哈尔滨 150001)

0 引 言

随着反导技术快速发展，面对敌方舰艇等目标配备的密集导弹防御系统，单一导弹突防变得愈发困难，而多导弹协同作战借助通信系统将多枚导弹构成一个作战网络，通过弹间通信使多导弹的打击时刻趋于一致，从而实现同时击中目标，这极大提高了导弹突防概率[1-2]。同时，相比于同等总装药当量的单枚导弹，借助于多点同时爆炸产生的爆炸聚集效应，多导弹协同作战还可显著提高导弹对目标的毁伤能力[3]。作为协同作战的关键技术之一，协同制导律在设计中有5个问题值得研究，分别为有向通信拓扑、无导弹-目标径向速度测量、带视线角约束、可打击移动目标和有限时间协同。

由于实战中相邻导弹间的通信距离存在差异，它们间的通信往往是有向的，因而设计有向通信拓扑下的协同制导律更贴合实际需求[4]。针对有向通信拓扑下的协同制导问题目前国内外学者研究成果较少，Zhao等[4]基于二阶多智能体协同控制理论和传统的比例制导律设计了有向拓扑下分布式协同制导律。彭琛等[5]在打击时刻控制制导律(ITCG)的基础上，基于有向图和加权平均一致性协调算法设计了有向拓扑下的分布式协同制导律。文献[4-5]如能使各导弹的时间协调变量在有限时间内达到一致，则可使各导弹的打击时刻更快趋于一致。

无导弹-目标径向速度测量制导律可以避免径向速度测量传感器的使用，从而减少导引头的成本和复杂度，提高系统的可靠性[6]。另外，还可作为径向速度测量传感器失效后的备用制导算法。针对无导弹-目标径向速度测量的协同制导问题目前国内外研究比较有限，周锐等[7]基于网络同步原理设计了一种协同制导指令，虽无需知道导弹-目标径向速度信息，不过需要明确了解目标的速度信息，实际中该信息较难准确测量。

带视线角约束可使得反舰导弹从期望的方向对舰艇目标进行打击，从而提高导弹的突防能力和对目标的毁伤能力[8]。针对带视线角约束的协同制导问题，Wang等[9]通过在比例导引律和带角度约束导引律基础上附加一项本导弹与相邻导弹打击时刻误差控制项设计了一种分布式协同制导律。张春妍等[10]利用各导弹的剩余飞行时间之差对带视线角约束的偏置比例导引律中的比例系数进行调节，提出一种协同偏置比例导引律。文献[9]-[10]所提协同制导律的末端视线角仅能渐近收敛于期望值，而非有限时间收敛。

由于越来越多的敌方目标可进行移动，因而有必要设计可打击移动目标的制导律[11]。针对可打击移动目标的协同制导问题，孙雪娇等[12]基于网络同步原理设计了一种多导弹位置同步算法，同步的平衡解即为移动目标的位置。Zhao等[13]通过在传统比例制导律基础上增加目标移动项和时间协同项设计了协同制导律。赵启伦等[14]采用改进比例导引法使领弹能够打击移动目标，然后基于二阶一致性算法设计协同制导律，使得从弹位置和速度能够跟踪领弹。文献[12]-[14]所提制导律虽能够打击移动目标，而未带视线角约束。宋俊红等[15]基于一致性理论提出了一种针对移动目标的制导律，而该制导律要求通信拓扑始终无向，实际中目前较难实现。

有限时间协同可使多导弹的打击时刻在导弹击中目标之前达到一致，有利于提高弹群整体突防概率，同时还可提高导弹制导精度和抗干扰能力。针对有限时间协同制导问题，Zhang等[16]基于一阶多智能体协同控制理论提出一种有限时间协同制导律，Hou等[17]基于时变比例导引法提出一种有限时间协同制导律。文献[16]-[17]虽能实现有限时间协同，而未带视线角约束。

目前，国内外学者针对同时考虑上述5个问题的协同制导律研究成果相对较少，受文献[1-24]启发本文对其进行研究。首先，在视线方向，基于二阶多智能体协同控制理论设计了有向拓扑下无需导弹-目标径向速度测量的多导弹有限时间分布式协同制导律，并给出了相应的稳定性证明。然后，在视线法向方向，基于积分滑模控制理论设计了带视线角约束且能打击移动目标的制导律，并给出了相应的稳定性证明。最后，通过仿真校验了所设计协同制导律的有效性。

对本文所提方法的优势进行说明，首先，同时考虑了上述5个问题，考虑问题更全面，更贴合实际需求；其次，无需测量目标的速度和加速度等信息，可降低雷达导引头的成本和复杂度;采用分布式通信，降低了对弹间通信距离的要求，提高了弹群的整体突防能力;制导律随时间连续变化，避免了制导指令抖振。

1 协同制导模型

目前，国内外在导弹变推力固体火箭发动机技术方面不断取得突破[18]。为简化研究，本文采用运动学分析方法，基于以下假设[13]：

(1)导弹和目标视为二维平面内质点；

(2)导弹导引头和自动驾驶仪动力学与制导回路相比响应足够快；

(3)每枚导弹的推力大小可控。

导弹与目标的相对运动几何关系如图1所示。

图1 多导弹与目标拦截几何示意图Fig.1 Multiple missiles-target engagement geometry

图1中Mi和T分别代表第i枚导弹和目标，ri代表Mi与T之间的相对距离，qi代表Mi的视线角，vmi和vt分别代表Mi和T的速度，θmi和θt分别代表Mi和T的弹道角，ami和at分别代表Mi和T的法向加速度。其中，i=1,2,…,n,n为导弹总枚数。

由图1得到Mi与T的相对运动方程如下：

(1)

(2)

(3)

(4)

将式(1)和式(2)分别对时间进行求导，并与式(3)和式(4)相结合可得

(5)

(6)

式中：uri和wri分别为Mi和T的加速度在视线方向的分量，uqi和wqi分别为Mi和T的加速度在视线法向的分量。

假设目标作匀速直线运动，则有

wri=0,wqi=0

(7)

(8)

本文研究系统(8)。首先，在视线方向设计无需测量x2i的制导律uri，以使x1i及x2i在有限时间内达到一致。然后，在视线法向方向设计无需测量x2i的制导律uqi，以使x3i及x4i在有限时间内收敛到0。最后，将得到的uri和uqi都代入到系统(8)中并通过仿真验证所设计制导律的有效性。

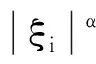
2 协同制导律设计

2.1 视线方向制导律设计

多导弹间通信拓扑关系可由图G(A)=(v,ξ,A)来描述，其中v描述节点组成的集合，ξ代表节点之间的连线，矩阵A=[aij]∈Rn×n代表权系数矩阵，其中i,j∈{1,2,…,n}。若导弹i和导弹j之间能够进行信息交换则aij>0，否则aij=0，特别aii=0。若存在某些实数θi>0，使得θiaij=θjaji对任意i,j都成立，则称图G(A)是细节平衡的[19-20]。定义图G(A)对应的拉普拉斯矩阵为L=[lij]∈Rn×n，其中矩阵的元素为

(9)

引理1[21]. 如果有向图G(A)是强连通且细节平衡的，则存在一个正的列向量θ=[θ1,…,θn]T使得θiaij=θjaji对任意的i,j∈{1,2,…,n}都成立，因而存在Θ=diag(θ1,θ2,…,θn)使得ΘL=(ΘL)T。

引理2[22]. 若有向图G(A)为强连通，则其拉普拉斯矩阵L的秩rank(L)=n-1。

由式(8)可得Mi的协同制导模型如下：

(10)

协同制导的目标是使得多导弹的打击时刻tfi在多导弹击中目标前达到一致，tfi可由下式表示：

tfi=tgoi+t

(11)

式中：tgoi为Mi的剩余飞行时间。由式(11)可得

tfi-tfj=tgoi-tgoj

(12)

由式(12)可知，如果能控制多导弹的tgoi达到一致就可使其tfi达到一致，从而实现同时击中目标，tgoi可由下式估计得到：

(13)

本节的制导律设计目标是，针对每枚Mi的视线方向制导模型，设计无需测量x2i的视线方向制导律uri使得

(14)

从而使式(13)中所示的所有导弹的tgoi在有限时间内达到一致。

下面以定理的方式给出视线方向协同制导律及其稳定性证明。

定理1. 针对系统(10)，如果有向图G(A)是强连通且细节平衡，则设计如式(15)～(18)所示的视线方向分布式协同制导律uri，可使x1i和x2i在有限时间内达到一致且无需测量x2i.

(15)

(16)

(17)

(18)

式中：l1r>0,l2r>0,k1r>0,k2r>0, 0.5<σr<1。

证. 将式(15)～(18)与式(10)相结合，令x1=[x11,x12,…,x1n]T,x2=[x21,x22,…,x2n]T,δr=[δr1,δr2,…,δrn]T,ηr=[ηr1,ηr2,…,ηrn]T可得

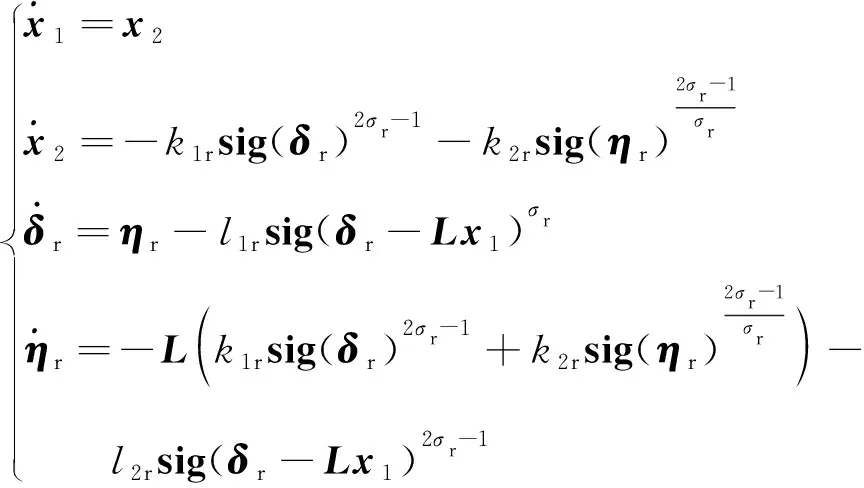
(19)

式中：L∈Rn×n为图G(A)的拉普拉斯矩阵。

令ex=δr-Lx1,ey=ηr-Lx2，则有

(20)

针对系统(20)，有如下Lyapunov函数

(21)

由于σr>0且l2r>0，因而V1r是正定且径向无界的。结合式(20)和式(21)，将V1r对时间求导可得

(22)

(23)

令rT=[r1,r2,…,rn]且满足

rTL=0

(24)

rT1=1

(25)

同时，令

X1=Mdx1,X2=Mdx2

(26)

式中：

Md=In-1rT

(27)

再结合式(26)，则式(23)可转化为：

(28)

将式(25)～(27)相结合并化简可知，系统(19)的状态x1i和x2i各自在有限时间内达到一致，等价于系统(28)的状态X1和X2各自在有限时间内收敛到0。

为证明X1和X2各自可在有限时间内收敛到0，选取Lyapunov函数形式如下：

(29)

LMd=L=MdL

(30)

(31)

X2=k1，k∈R

(32)

将式(25)和式(27)相结合可得

rTMd=rTIn-rT1rT=0T

(33)

由式(26)和式(33)可得

rTX2=rTMdx2=0

(34)

将式(32)和(34)与式(25)相结合可得

X2=0

(35)

定理1中uri的第1项用于补偿系统中的非线性特性，第2项用于调整多导弹的x1i和x2i使其各自在有限时间内达到一致。

2.2 视线法向制导律设计

由式可得Mi视线法向制导模型如下：

(36)

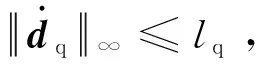
式中：dqi=-2x2ix4i/x1i为系统非线性特性所产生的干扰，所有导弹视线法向受到的干扰由dq=[dq1,dq2,…,dqn]T表示。

本节制导律设计目标是，针对每枚Mi视线法向制导模型，设计无需测量x2i的视线法向制导律uqi使得

(37)

接下来以定理的方式给出视线法向制导律及其稳定性证明。

(38)

(39)

(40)

式中：k1qi>0,k2qi>0,k3qi>0,k4qi>lq, 0<αqi<1。

证. 将方程(40)对时间求导可得：

(41)

令

zqi=ρqi+dqi

(42)

然后由式(36)、式(38)、式(39)、式(41)和式(42)可得：

(43)

选取Lyapunov函数如下

(44)

式中：Pqi∈R2×2>0,ξqi可由下式表示

(45)

将上式中ξqi对时间求导，并结合式(42)和式(43)可得

(46)

式中：

(47)

将式(44)中Vq对时间求导，并结合式(46)可得

(48)

由于k3qi>0且k4qi>lq，式(47)中矩阵Aqi的所有特征值均具有负实部，因而由线性定常系统Lyapunov定理可知，对任意的正定对称矩阵Qqi都有唯一的正定对称矩阵Pqi使得

(49)

故式(48)可写为

(50)

标准二次型不等式形式如下

(51)

(52)

由式(51)和式(52)可知

(53)

由式(45)和式(51)可知

(54)

由于

(55)

将式(53)～式(55)与式(50)相结合可得

(56)

式中：

(57)

由式(44)和式(56)并结合有限时间稳定性理论可知

(58)

式中：

(59)

将式(45)与式(58)相结合可知

(60)

由式(60)可知

(61)

将式(61)与式(41)相结合可得

(62)

再由文献[23]的引理2可知当x3i和x4i到达滑模面后可在有限时间内收敛到0，因而x3i和x4i从初始时刻开始可在有限时间内收敛到0。定理证毕。

定理2中uqi的前2项可使x3i和x4i在有限时间内收敛到0，第3项和第4项用于抵消干扰dqi对系统带来的影响。

注2虽然定理1和定理2并没有给出有限时间上界，但并不影响制导律的实际使用，实际中通常通过调节制导律参数来调整系统收敛时间使其满足要求。

注3在导弹3维制导律设计中，可将导弹的3维运动分解成视线方向和视线法向(高低、方位)3个方向，每个方向均为2阶系统，视线方向可采用定理1方法，视线法向(高低、方位)可采用定理2方法。因此，本文的2维制导律设计方法同样可用于3维制导律设计。

注4实际中制导律与控制律分开，通常制导律在理想条件下进行设计，设计控制律时才会将大气扰动等各种不利因素考虑进去，以使导弹实际过载能实时跟踪制导律产生的期望过载。本文针对制导律进行设计，因而未考虑上述因素影响。

3 仿真校验

为验证本文所提出的多导弹协同制导律的有效性，在不考虑外界干扰、测量噪声和执行机构控制精度等因素影响的理想条件下，针对3枚反舰导弹在水平面内均从各自期望的方向同时攻击一艘匀速直线运动舰艇目标的情形进行仿真，仿真步长取定步长5 ms。视线方向制导律参数取为k1r=10,k2r=10,l1r=5,l2r=5,σr=0.68，视线法向制导律参数取为k1qi=2,k2qi=10,k3qi=5,k4qi=1,αqi=0.95，其中，i=1,2,3。

图2 3枚导弹间的通信拓扑结构Fig.2 Communication topology for three missiles

目标和导弹的初始条件分别如表1和表2所示，目标作匀速直线运动。

表1 目标初始条件Table 1 Initial conditions for target

表2 导弹初始条件Table 2 Initial conditions for three missiles

3枚导弹的脱靶量、打击时刻和视线角误差由表3给出。可见它们的脱靶量都保持在0.22 m范围之内，打击时刻可以达到一致，视线角误差均在2×10-3(°)范围之内，说明在理想条件下，本次仿真中所有导弹可以从期望的方向同时击中移动目标。

表3 协同制导仿真结果Table 3 Simulation results of cooperative guidance

4 结 论

本文针对有向拓扑下多导弹从各自期望的方向同时击中移动目标且无需测量导弹-目标径向速度问题进行研究。首先，设计了视线方向分布式协同制导律，并通过稳定性理论证明其可保证所有导弹的打击时刻在有限时间内达到一致。然后，设计了视线法向制导律，并通过稳定性理论证明了其可保证所有导弹的视线角在有限时间内收敛到期望值。最后，通过仿真校验了所提方法在理想条件下可使有向拓扑下的多导弹从各自期望的方向同时击中移动目标。未来将对考虑导弹间通信拓扑切换的协同制导律和三维协同制导律设计问题进一步研究。

图3 协同制导仿真结果Fig.3 Simulation results of cooperative guidance