基于时变间距和相对角度的无人车跟随控制方法研究

李润梅 张立威 王剑

近些年来,车路协同系统(Cooperative vehicle infrastructure system,CVIS)的相关技术发展迅速.车辆之间可以互相感知和通信,且车辆和道路以及道路和两旁设施之间也能够互相感知和通信[1].在CVIS下,结合无人驾驶技术必将推动无人车的快速发展和传统交通流的变革.目前,国内外的自动驾驶技术已经相当成熟,谷歌无人车项目是这些成功案例之一,谷歌无人驾驶汽车(Google driverless car)是谷歌公司的Google X实验室研发的全自动驾驶汽车,不需要驾驶者就能启动、行驶以及停止[2].谷歌的工程人员使用7辆试验车,其中6辆是丰田普锐斯,一辆是奥迪TT,在加州几条道路上进行测试.测试结果表明,这些车比有人驾驶的车更安全,因为它们能更迅速、更有效地做出反应.在这些背景下,无人车编队控制成为了该领域的研究焦点之一.车辆编队行驶能够提高道路交通的容量和安全性,其中车辆跟随控制是编队行驶的关键问题,车辆跟随控制包含横向控制、纵向控制以及横纵向综合控制.

在车辆的横向控制研究中,一个广泛关注的问题是转向控制的精确性[3−5].王家恩等提出了一种跟踪期望横摆角速度的车辆横向控制方法,基于7个自由度的车辆动力学模型,设计滑模控制器跟踪期望横摆角速度,使得车辆稳定地跟踪目标路径[3].刘伟等简化了汽车运动学模型,设计滑模控制器对无人车的横向运动进行控制,实现了无人车的路径跟踪[4].田涛涛等提出了一种无模型自适应控制方法控制无人驾驶汽车的横向运动,获得了很好的效果,并且实际应用于清华大学无人驾驶汽车实验平台,在横向控制方面做出了很大的突破[5].王家恩等[3]、刘伟等[4]和田涛涛等[5]都考虑了车辆的横向控制,可以看出无人车横向控制的研究已经很成熟.

在车辆纵向控制中,主要是车辆速度和间距的控制.Nouveliere等使用一个二阶滑模技术去控制实验车辆的纵向行驶,考虑了车辆之间的距离和车辆的速度有关,使用Matlab仿真软件和一个配有传感器和执行机构的车辆原型进行仿真验证,可以很好地实现车辆行驶和停止、避障停车以及多车跟随[6].Li等使用了反馈控制算法实现了两轮驱动型无人车的纵向跟随行驶,两无人车之间的间距设置为一个固定值,两无人车之间的相对角度也是恒定的[7].Peters等考虑了跟随车的行驶不仅和其前面一辆车有关,还与第一辆车有关.实现了具有恒定间隔策略的循环纵向队列保持稳定行驶.

在实际道路中车辆是沿着任意轨迹前进行驶的,道路条件复杂,比如笔直的道路,弯曲的道路以及颠簸的道路等,所以考虑车辆的横纵向综合编队行驶更具有实际意义[8].

领航跟随模式对于解决车辆横纵向综合编队行驶是一种简单且有效的建模方法.其原理是将车队中的某一辆车作为领航车,其他车都作为跟随车,然后设计跟随车的控制器去实现跟随车跟随领航车的速度和方向.这个模式的核心思想是在车辆行驶过程中,将编队问题转化为跟随车和领航车保持一个特定的相对距离和角度行驶的问题.所以,跟随车的速度和方向控制是这个模式的关键所在.领航跟随模式由Wang首次提出,他使用导航策略对编队中自治移动的机器人进行控制[9].随后,这个方法被应用到了车辆编队领域.No等使用领航跟随模式结合李雅普诺夫函数实现了车辆的纵向行驶,具体是用李雅普诺夫稳定性理论去推导出一个控制律,用它去控制两车之间的距离,最后仿真了4辆车的列队行驶[10].任殿波等在假定车队中的每个被控车辆能够接收到领航车以及该车前面一个车辆的位移、速度和加速度信息的情况下,应用滑模变结构控制方法得到了关于车辆间距误差的车辆纵向跟随系统数学模型.然后利用非线性关联大系统的稳定性判定条件来设计控制参数,保证了车辆纵向跟随控制系统的稳定性[11].任殿波等在之前研究的基础上,基于非线性车辆纵向动力学模型,采用固定车辆间距跟随策略,设计了车辆跟随系统的纵向滑模控制律;应用向量Lyapunov函数方法和比较原理,对一类无限维非线性关联系统的稳定性进行研究.仿真结果表明设计的车辆纵向跟随控制律能使车辆速度误差和间距误差具有较快的收敛速度[12].Xuan和Lu在系统中每个元素只能获得相对局部信息的条件下提出了一个车辆跟随控制方法.并且为了增加车辆跟随系统的可扩展性,在提出的控制方法上添加了速度约束.他们在微型交通环境下建立了一个包含5辆微型智能车的车辆跟随系统去验证他们提出的控制方法[13].但No等[10]、任殿波等[11−12]和Xuan等[13]的研究都是以两车之间的相对距离和相对角度是常量为前提的.但在实际行驶过程中,无人车之间的相对距离和角度不是固定的常数.

以往研究者是在两车之间期望相对距离或角度是常数的基础上建立误差模型,而本文建立的模型是基于时变的两车期望相对距离和时变的期望相对角度建立.将时变的期望相对距离和角度作为输入,给定领航车的前进轨迹,让领航车做变加速行驶,设计控制系统,输出跟随车的前进速度和横摆角速度,控制系统的作用是在无人车之间保持期望的相对距离和角度的前提下,跟随车的速度和角速度可以很好地跟踪领航车的速度和角速度,而且跟踪误差能够很快地渐近收敛到0.

本文的主要贡献总结如下:结合车辆的实际行驶情况,将无人车之间的期望相对距离和角度作为时变量输入,建立无人车的领航跟随误差模型.基于建立的误差模型,使用反馈控制法结合李雅普诺夫第二法设计出跟随车的速度控制器和角速度控制器.最后,用Matlab对跟随车的跟随效果进行仿真验证.

本文的结构如下:第一部分建立了无人车的领航跟随误差模型;第二部分介绍了怎样得到时变的期望相对距离和角度;第三部分用反馈控制法和李雅普诺夫第二法设计了两个速度控制器,并且使用李雅普诺夫函数和Barbalat引理从理论上验证了控制器的稳定性和跟踪误差的渐近收敛性;第四部分展现了仿真背景,仿真设计和仿真结果分析;第五部分是总结.

1 领航跟随误差模型

无人车的领航跟随结构[14]如图1所示.

在图1中,L(t)是跟随车中心到领航车中心的距离,表示跟随车和领航车的相对距离.ϕ(t)是领航车中心轴线和相对距离连线的角度,表示跟随车和领航车的相对角度.Gl(xl,yl)和Gf(xf,yf)分别是领航车和跟随车的中心点.车身长度为2h,h是车辆中心到车辆前轴的距离,它等于车辆中心到车辆后轴的距离.针对给定车型,h为常数.θl(t)和θf(t)分别是领航车和跟随车相对于x轴方向的夹角即横摆角.φl(t)和φf(t)分别是领航车和跟随车的行驶方向与它的前轮方向的夹角即转向角.vl(t)和vf(t)分别是领航车和跟随车的速度,ωl(t)和ωf(t)分别是领航车和跟随车的角速度.此运动学模型的建立基于以下三个假设条件:1)车轮没有滑动;2)前轮负责转向,后轮负责驱动;3)领航车的前进轨迹和速度是已知的.后文中,为了减少公式的长度,将所有公式中的自变量时间t予以省略.

图1 无人车领航跟随结构Fig.1 Leader-follower structure of unmanned cars

如图1所示,在跟随车的前进方向和与前进方向垂直的方向上,可以将相对距离L分解成两个分量.两车之间的跟踪误差如式(1)所示.分别指的是相对距离横向分量的期望值与实际值之差,相对距离纵向分量的期望值与实际值之差,领航车与跟随车的横摆角之差.是相对距离L的期望值的两个分量.

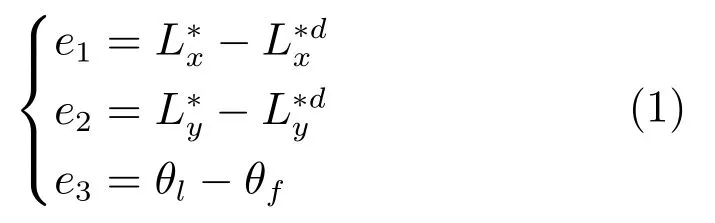
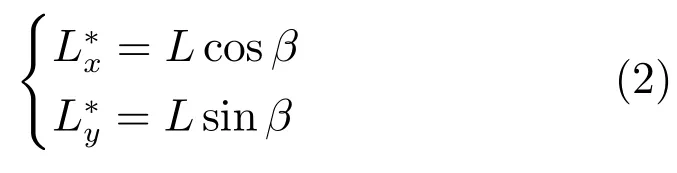
将式(2)代入到式(1)中,得式(3):

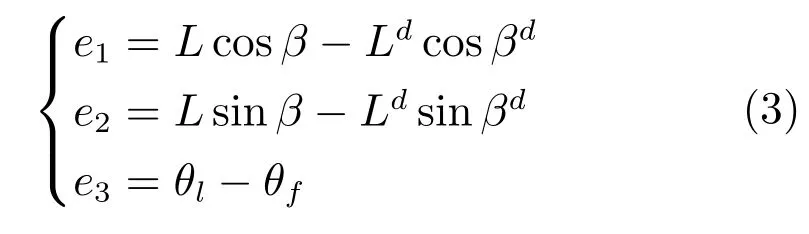
其中Ld是无人车之间期望的相对距离,对式(3)求导可得到式(4).

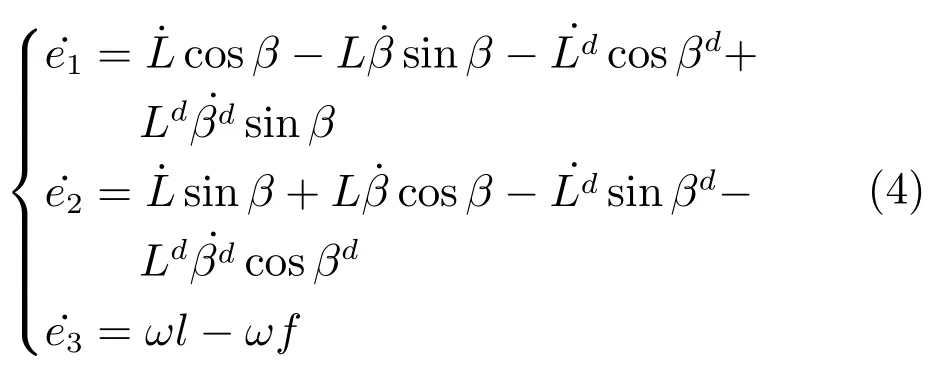
为了得到相对距离L的导数,在平面坐标系中将L沿着水平方向和垂直方向分解成Lx和Ly.可以得出如式(5)所示的几何关系.

对式(5)求导,可以得到式(6).

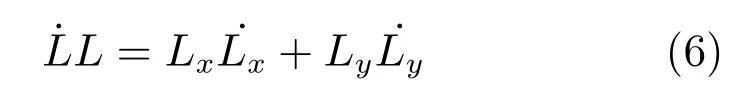
由图1可以看出,Lx和Ly这两个分量可以写成式(7)和式(8)的形式,

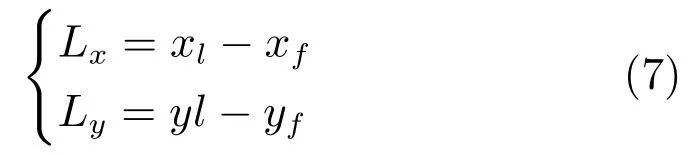
和

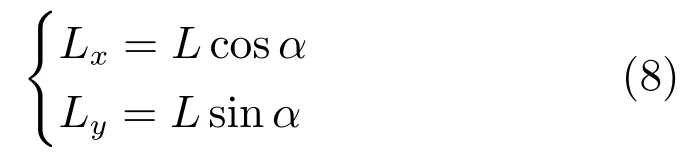
根据图1中各角度的相互关系,可以得到β=ϕ+e3−π/2,θf=α−β+π/2以及θl=α−ϕ+π.将式(8)、式(7)的导数代入到式(6)中,结合积化和差公式与各角度关系,可以推出相对距离L的导数如式(9).

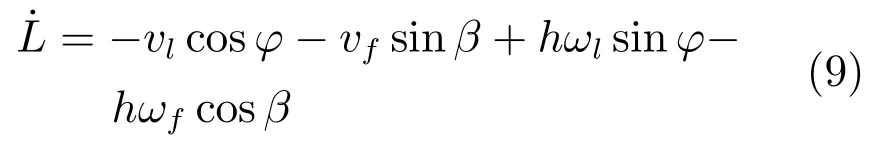
相对角度ϕ如式(10),

将式(10)求导可以得到式(11).

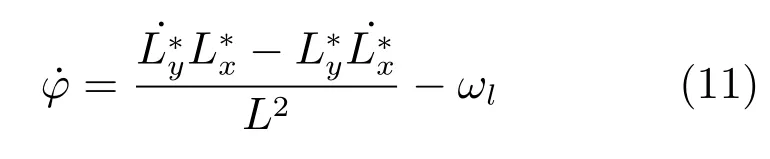
由式(3)可以推出相对距离的表达式如式(12).

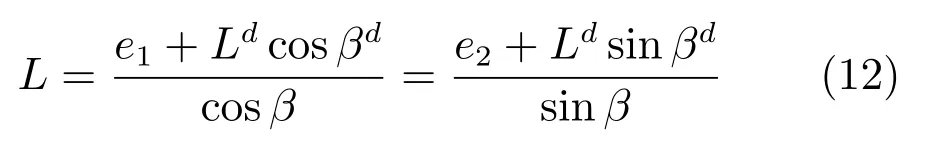
把式(2)、式(9)和式(11)代入到式(12)中,并结合积化和差公式与各角度关系可以推出相对角度ϕ的导数表达式,如式(13).

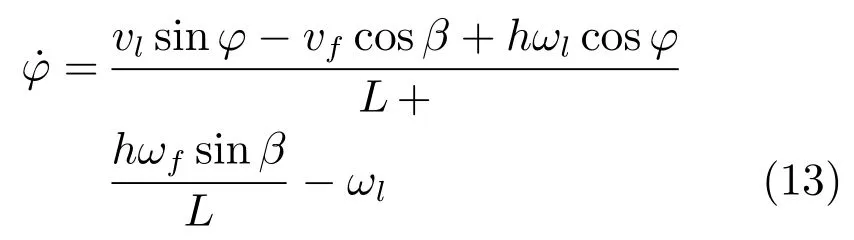
由β和ϕ的关系,得到β的导数表达式如式(14).

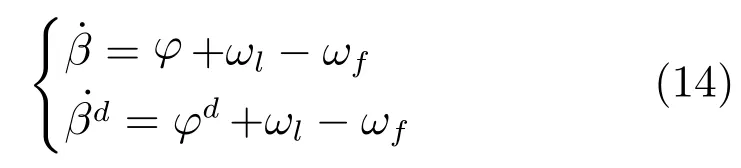
将式(9)、式(13)和式(14)代入到式(4)中,可以推出无人车的领航跟随误差模型,如式(15).

式(15)即为无人车的领航跟随误差模型,接下来通过设计控制器,给定时变的期望相对距离和期望相对角度,使得跟随车能够按照领航车的前进轨迹跟随领航车.

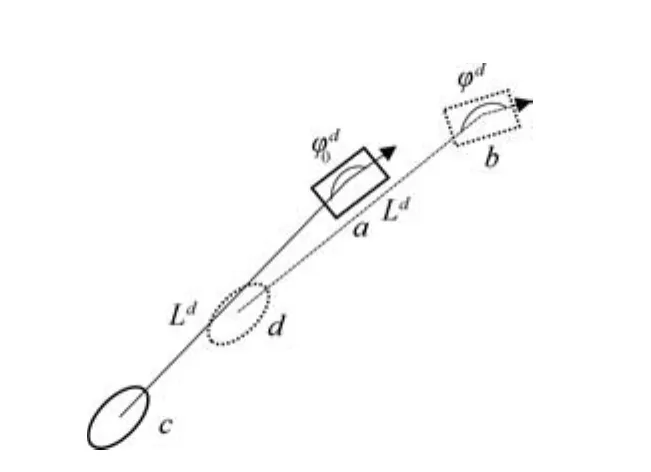
图2 时变期望相对角度简化示意图Fig.2 Simplified schematic of time-varying relative angle

2 时变的期望相对距离和角度

2.1 时变的期望相对距离

期望相对距离是指在确保行车安全的情况下,车辆间要保持的最小距离,无人车在实际行驶过程中,车之间的期望相对距离是时变的.本文参考了文献[15]给出的理想间距公式,期望相对距离与前车和后车的相对速度、前车的速度以及后车的速度相关,如式(16).

其中vf是跟随车的速度.vl是领航车的速度,vrel=vf−vl是二者的相对速度.

针对本文跟随车的跟随控制问题,领航车的速度是给定的,跟随车的速度是由控制系统得到的,考虑到设计控制器的目的之一是为了使跟随车的速度无限接近领航车,故将式(16)简化,设vrel为0,得到式(17).

其中Ld是两车之间的期望相对距离,vl是领航车的速度.同时因为在仿真中速度的单位是m/s,但在实际的高速路上,汽车速度的单位是km/h,经过单位转换.

2.2 时变的期望相对角度

在实际道路上,当领航车改变方向时,无人车之间的相对角度也在变化.为了解决方向跟随问题,文献[16]给出了期望相对角度的表达式.图2是时变期望相对角度简化的示意图,假设长方形代表领航车,领航车从位置a行驶到位置b,假设椭圆形代表跟随车,跟随车从位置c行驶到位置d.将b定义为ϕd,初始的相对角度已知,这两个的差值表示为式(18).

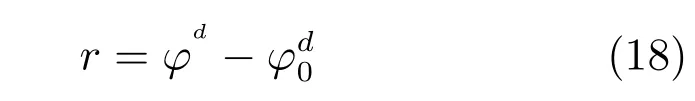
其中,r为转弯半径,由图1可以得到式(19).

根据无人车之间的位置关系图(2)所示和跟随车的运动规律可以得出式(20).

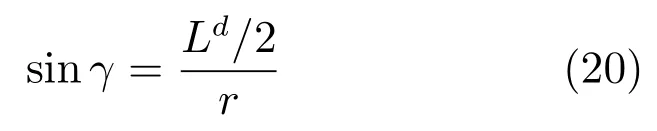
将式(18)和式(19)代入式(20),可以推出期望相对角度ϕd如式(21).

由式(21)可以看出,期望相对角度与期望相对距离、领航车的速度以及角速度有关,它是一个时变量.

3 反馈控制器设计

文献[17]给出反馈控制的思想和过程.反馈控制法是将系统的输出信息反馈到输入端,与输入信息进行比较,并利用二者的偏差进行控制的过程.无人车跟随控制系统如图3所示,本文在无人车之间的期望相对距离和角度输入为时变量的条件下建立了无人车领航跟随误差模型如式(15),不考虑其他外界因素的影响,如噪声和扰动,根据建立的误差模型,本文将使用简单且更接近于实际应用的反馈控制法和李雅普诺夫第二法去设计跟随车的速度控制器和角速度控制器,由误差模型和反馈控制方法可以推出式(22)和式(23).

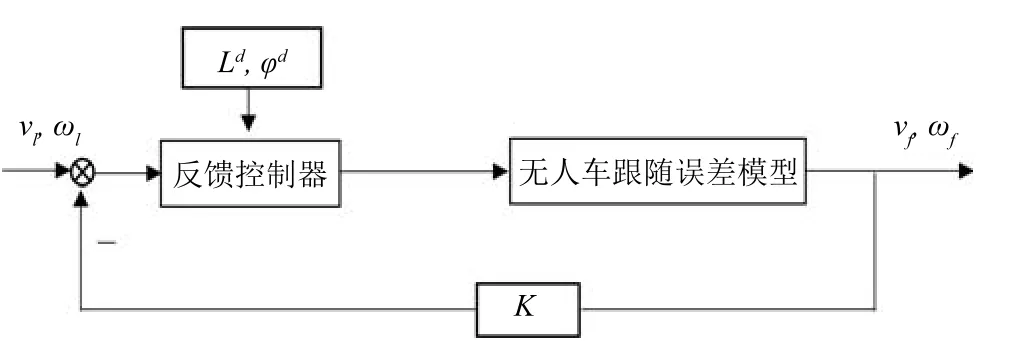
图3 无人车跟随控制系统Fig.3 Control system of unmanned cars following

K是式(23)的补充项,它是由李雅普诺夫函数如式(24)和李雅普诺夫函数的导数如式(25)得到的.常数k1和k2都大于0,本文使用李雅普诺夫函数从理论上去证明设计的控制器的稳定性同时推导出K的表达式.

选择李雅普诺夫函数如式(24).

常数k3大于0,从式(24)中可以看出V≥0.当且仅当时e1=e2=e3=0时,V=0.将式(24)求导可得到式(25).

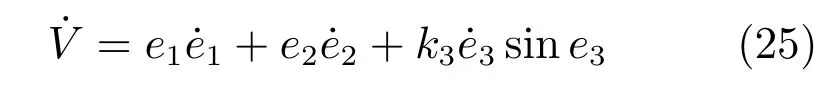
将式(15)、式(22)和式(23)代入到式(25)中,可得到式(26).

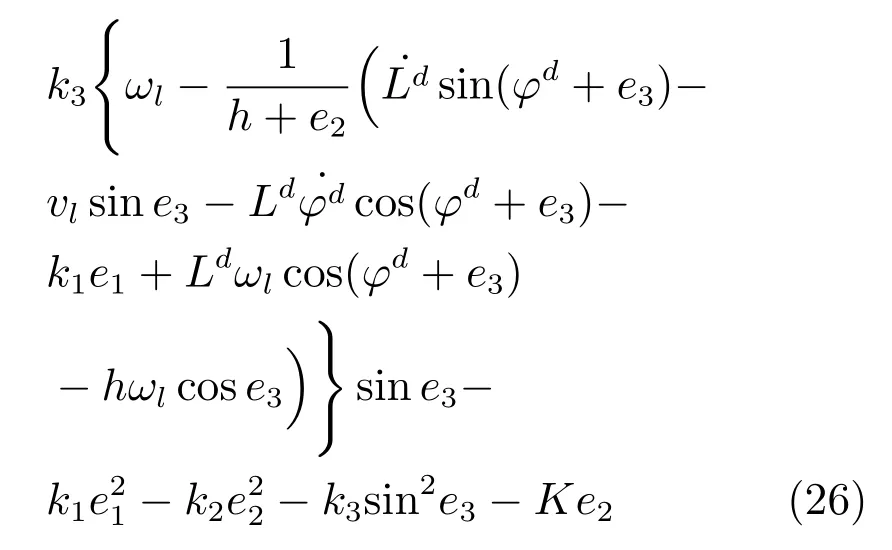
为了保证李雅普诺夫函数的导数小于等于0,则由式(26)结合放缩法可以推出K的表达式如式(27).

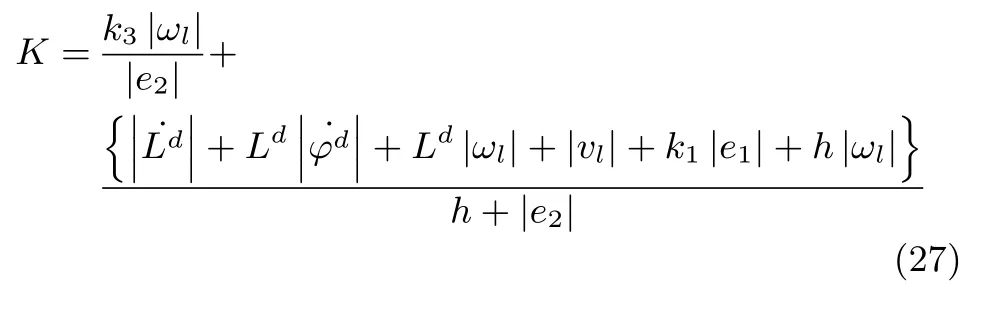
定义A如式(28),

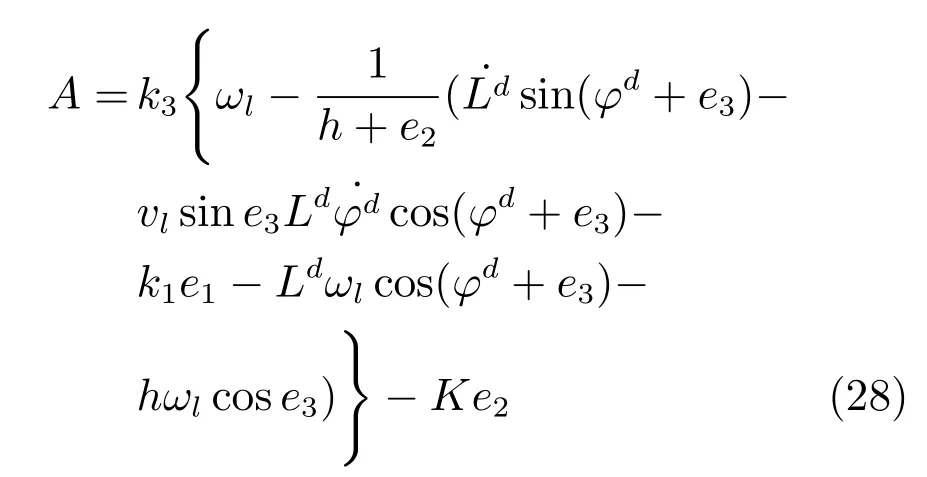
将式(27)和(28)代入到式(26),可以得出式(29).

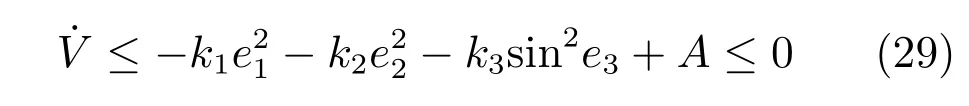
在实际的控制系统中,李雅普诺夫稳定性理论在分析稳定性和理论研究上被广泛使用,当是V正定且是半正定时,系统的有界稳定性可以由李雅普诺夫理论得出,但是不能得到控制系统是否是渐近收敛的.Barbalat引理克服了李雅普诺夫理论的局限性,在是半正定的情况下,它可以得出非线性时变系统的渐近收敛性[18].

引理.Barbalat引理的具体描述如下:

1)如果x(t)有界,并且是一致连续的(即,则当t→0时,成立.

2)如果x(t)和都有界,且,其中M(x)是一个连续正定函数,则当时t→0,x(t)→0成立.

证明.由式(29)可以得到式(30)的关系.

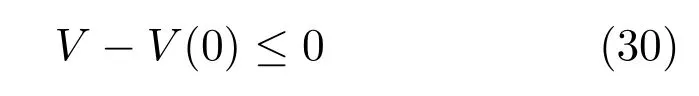
将式(24)代入到式(30)中,可以得到式(31).

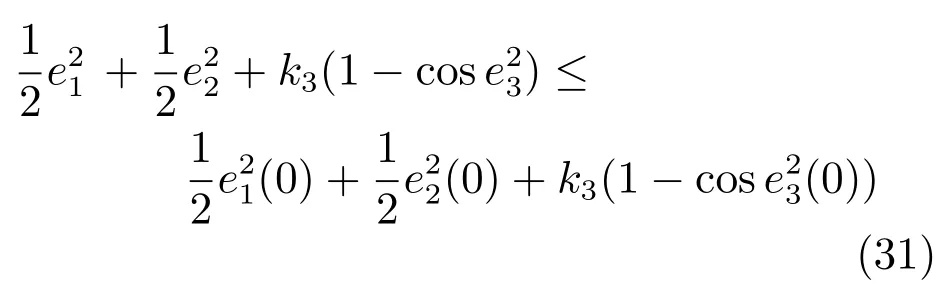
因为e1(0),e2(0),e3(0)∈L∞成立,所以由式(31)可以得到e1,e2,e3∈L∞.然后又由式(29)可以得出式(32).

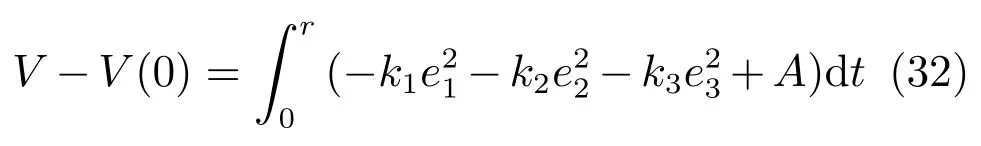
将式(32)转化成式(33).

V(0)是一个常数,通过式 (33)可以看出成立.又结合式(4),可以得到,综上可以得出e1,e2,e3这三个误差是一致连续的.

根据Barbalat引理并结合上述证明可知,当t→∞时,成立,当t→∞时,e1,e2,e3→0也成立.综上,基于两车领航跟随误差模型的控制器稳定性可从理论上得到证明,且本文的控制器能够从理论上使控制系统的跟踪误差渐近收敛于0.

4 Matlab仿真验证

在上一节中,已经用李雅普诺夫第二法和Barbalat引理从理论上证明了控制系统的稳定性和渐近收敛性.因为无人车之间期望的相对距离和角度都是时变的,本文将这两个时变量代入到设计的控制器中进行仿真,并且将这两个时变量也进行了仿真.考虑到实际行驶过程中存在量测噪声,量测噪声会影响领航车的车速传感器准确检测车速,文献[19]也考虑到了噪声对车辆编队的影响.所以本文主要从两个方面进行仿真.首先,在不考虑量测噪声的理想情况下进行仿真验证.其次,将量测噪声加入到控制系统,仿真量测噪声对控制系统的影响.其中,初始化参数编程实现,反馈控制器和两无人车跟随误差模型通过搭建Simulink实现.

Simulink模型搭建过程:先搭建领航车的行驶轨迹模块,再搭建反馈控制器模型,因Simulink模型太大,限于篇幅,以反馈控制器Simulink为例如图4所示,其中常数是k1和k2.

图4 反馈控制器Simulink框图Fig.4 Simulink diagram of feedback controller

4.1 领航车的行驶轨迹

领航车沿着给定轨迹做变加速行驶,假设领航车的行驶轨迹如式(34).

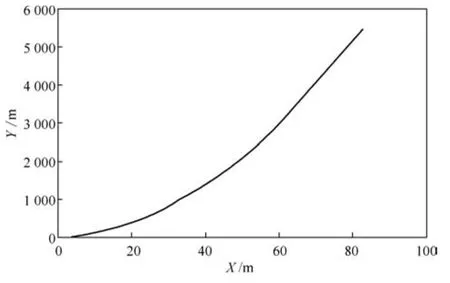
图5 领航车行驶轨迹曲线Fig.5 Travel trajectory curve of leader

4.2 领航车的加速度和速度

根据高速路上车辆正常行驶的状态,设置领航车以一个随时间变化的加速度av行驶,且保证两无人车加速度的变化幅度平稳,加速度曲线如图6所示.文献[20]也考虑到车辆在行驶时的加速度不仅仅是固定的或者为0,而是随时间变化的.

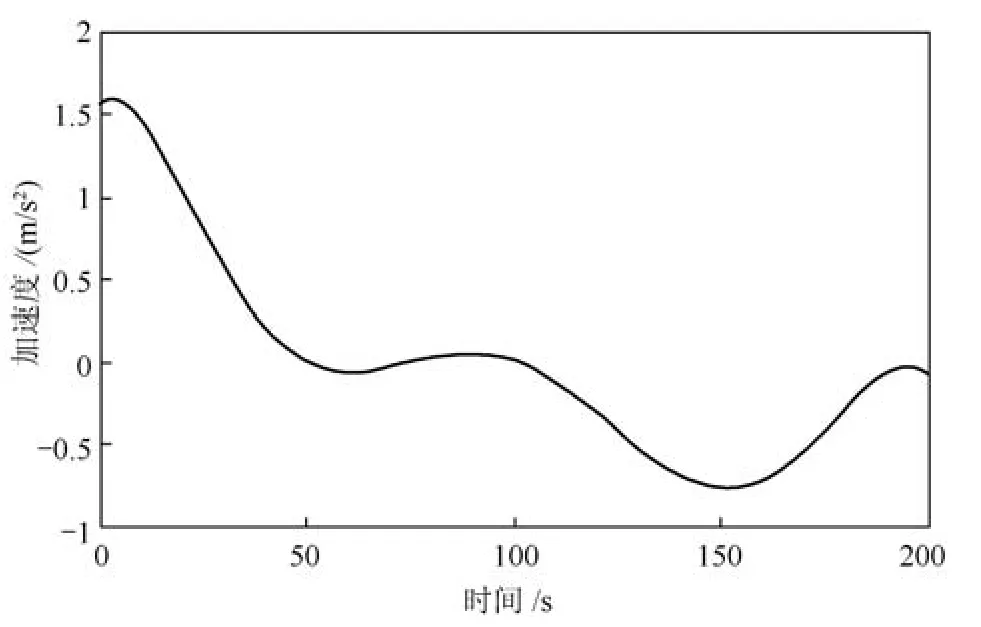
图6 领航车的加速度Fig.6 Leader's acceleration

假设两无人车刚开始是停止状态,领航车的初始速度设置0m/s,领航车的速度曲线也是随时间变化的,曲线如图7所示.

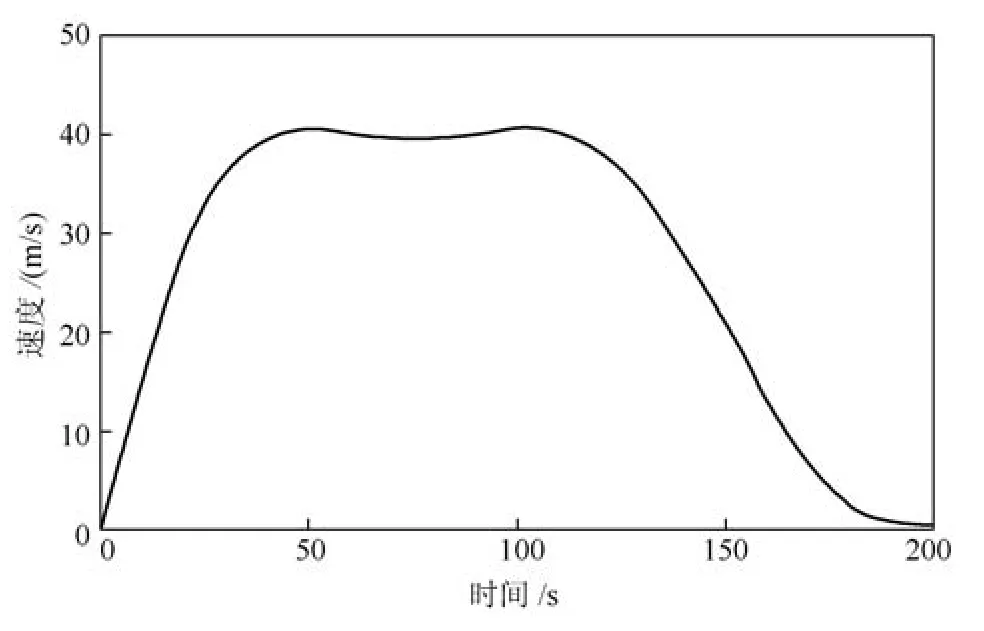
图7 领航车速度Fig.7 Leader's speed

4.3 时变的期望相对距离

两车的期望间距随着领航车车速的变化而变化,如式(17)所示,两车之间的实际距离与领航车速度的变化如图8所示.图8中,将100s前领航车加速领航过程称为前期,之后领航车减速领航的过程称为后期.两车初始距离为2m.

4.4 领航车的角速度

领航车的角速度与其行驶轨迹相关[21],由图1的几何关系可以得出式(35).

因为yl/xl=tanθl,结合式(34)和式(35)可以推出式(36).

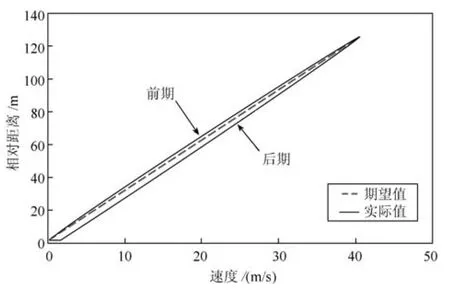
图8 两车相对距离与领航车速度关系曲线Fig.8 The relationship between relative distance between unmanned cars and the speed of the leader car

由式(36)可以推出领航车的角速度如式(37).

当xl(0)取给定时,可以得出和.

本文讨论的无人车是两驱车,前轮负责转向,后轮负责驱动,领航车的角速度仿真曲线如图9所示.

图9 领航车角速度Fig.9 Angular velocity of leader

4.5 时变的期望相对角度

根据式(21),期望的相对角度和无人车之间初始的相对角度、无人车之间的期望距离以及领航车的速度和角速度有关.期望相对角度的曲线如图10所示.当无人车开始行驶时,领航车在跟随车的正前方位置,两车之间的期望相对角度按照式(21)变化的.

图10 期望相对角度Fig.10 Expected relative angle

4.6 跟随车的速度

将无人车之间时变的期望相对距离Ld和角度ϕd代入控制器如式(22)和式(23),为了得出较优的仿真效果,经过多次设置参数实验,三个控制增益分别取为k1=1,k2=0.5,k3=0.01,可以仿真出跟随车速度和角速度曲线分别如图11(a)和图11(b)所示.

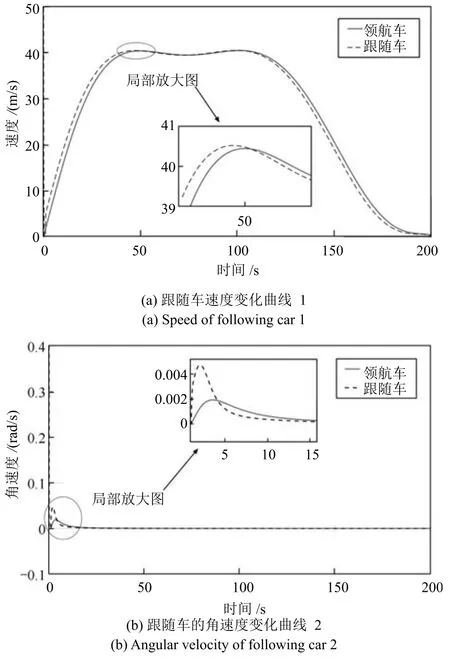
图11 两无人车的速度跟随曲线Fig.11 Velocity following of two unmaned cars

由图11(a),结合图8,分析跟随过程如下:

从领航车启动开始,两车实际距离大于期望距离.在领航车加速期间,领航车速度逐渐变大,期望相对距离也在逐渐变大,但两车实际间距一直大于期望值(如图8中虚线和标注“前期”的实线所示).所以跟随车速度一直稍大于领航车速度,力图使得实际距离逼近于期望距离.其根本原因在于初始距离使得两车实际距离大于期望距离,这个初始距离在跟随的过程中被消耗掉.反之,当领航车速度逐渐变小,跟随车的速度与二者的实际与期望距离表现为“后期”中,二者实际距离要稍小于期望距离,此时跟随车的速度要低于领航车,以增加实际距离.

由图11(b)可见,领航车的角速度和跟随车的角速度最大误差是0.034rad/s,之后跟随车的角速度都可以很好地跟随领航车.

显然,在两无人车之间的期望相对距离和角度是时变的情况下,本文方法对跟随车的速度及角速度起到了较好的控制作用.

4.7 控制系统的三个误差分析

为了更好地反映无人车的跟随控制效果,对包括相对距离横向分量的期望值与实际值之差e1、相对距离纵向分量的期望值与实际值之差e2和两车的横摆角之差e3.它们的仿真曲线如图12.

不考虑前2s调整过程,从图12(a)中可以看出两无人车之间的横向误差在17s后快速收敛到0,最大的横向误差为0.02m.从图12(b)中可以看出纵向误差在10s后快速收敛到0,最大的纵向误差是6.57m,且为负值,这在实际行驶过程中属于安全行为.从图12(c)中可以看出角度误差在40s后快速收敛到0,最大的角度误差为0.057rad.上述三个误差值在实际行驶过程中均是可以接受的.综上,仿真结果表明了本文提出的控制方法对无人车的跟随行驶有很好的控制效果.

4.8 两无人车的行驶路径

从图13中可以看出,跟随车沿着领航车的前进轨迹跟随行驶,为了去说明控制器的控制效果,本文使用了足够大的行驶距离进行仿真,纵向距离最大的仿真值为5500m.仿真结果又一次说明跟随车可以很好地跟随领航车.

5 结论与展望

图12 两无人车之间的三个误差Fig.12 Three errors between two unmanned cars

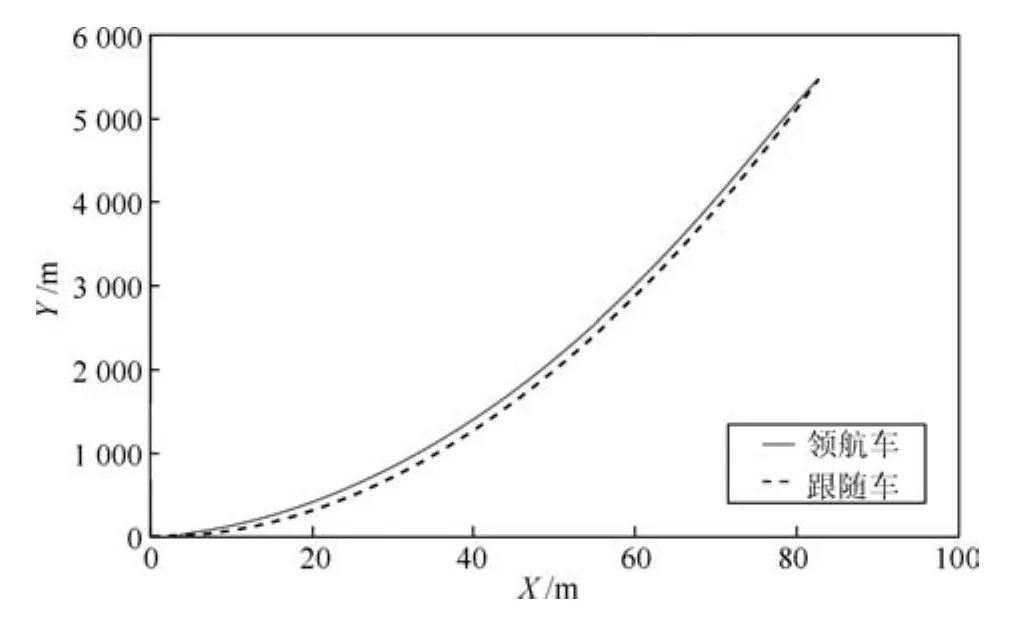
图13 两无人车之间的行驶路径Fig.13 Movement track of two unmanned cars

本文在建立无人车误差模型时,将无人车之间的期望相对距离和角度作为时变量输入,提出基于时变量的无人车跟随行驶方法.首先采用领航跟随模式建立了领航车与跟随车之间的误差模型,接着将无人车之间的期望相对距离期望相对角度设为时变量,使用反馈控制法和李雅普诺夫第二法设计跟随车速度控制器和角速度控制器,用Barbalat引理从理论上证明了跟踪误差渐近收敛.使用Matlab仿真软件对两无人车的跟随行驶进行仿真,仿真结果表明了跟随车可以很好地沿着领航车的前进轨迹跟随行驶.在后续的研究中,将考虑使用滤波方法或者加入抗干扰的控制算法对领航车车速传感器检测的速度中带有的噪声进行处理.