基于复杂网络的封闭小区交通开放策略探究

陈伟哲 李乡儒

随着我国经济快速发展,城市规模不断壮大,汽车数量也日益增多.2000年至2009年,我国城镇化率由36.2%提高至46.6%,年均增长约1.2%;北京、上海、广州、深圳、成都和杭州等城市的机动车保有量先后超过百万量级,全国民用汽车保有量从1609万辆增至6281万辆,年均增长16.3%[1].然而,我国许多地区居住模式主要为封闭式小区,封闭小区在上海占总居住小区的83%,广东省的封闭小区覆盖了70%以上的城乡面积及80%以上的人口[2].封闭式小区具有封闭性和自我完善性,小区内部道路系统呈现出内向型树状结构,多为断头路[3],仅有一两条主要道路(下称主道路)与城市道路网络连接.这些封闭小区切断了城市道路网络的“毛细血管”,使得交通流集中在少数的干道上.导致一旦干道出现交通拥堵,就很容易引起交通系统出现区域性瘫痪.

2016年国务院发布《关于进一步加强城市规划建设管理工作的若干意见》,提出“新建住宅要推广街区制”和“已建成的住宅小区要逐步打开”,引起强烈的社会反响.小区从封闭走向开放,需要解决许多问题.封闭小区该不该开放,应该开放哪些小区,如何开放能使不良影响较小且效益更大,以及开放后小区应该如何设计管理等诸多细节,不一而足.

目前关于封闭小区交通开放的相关研究主要集中在探讨该不该开放[3−4]以及开放后街区式住区的布局设计[5−6],而关于开放哪些小区、具体如何开放则讨论较少.正如文献[4]所言,为推进系统性改革,需要差异化地推行小区开放政策,对于什么类型、地点、面积、条件的小区需要开放,如何开放及开放后的问题如何解决,都要有不同的保障方案.本文利用复杂网络理论,从不同封闭小区开放策略对城市道路网络的效率及稳定性影响的角度探讨小区该不该开放、开放哪些小区以及如何开放的问题.

复杂网络理论从拓扑结构的角度对网络进行分析,把微观和宏观性质联系起来,能预测复杂系统丰富的整体行为.若把复杂网络理论的研究方法应用到道路网络,需要进行实证研究,说明城市道路网络具有复杂网络特性.文献[7]对具有不同形态和历史背景的6个城市的道路交通网络进行了拓扑分析,发现这些网络均为无标度网络[8],并且表现出小世界特性1小世界特性指具有低平均路径长度、高聚类系数.文献[9]对美国40个城市道路网络进行了大范围的分析,也发现类似的性质.Crucitti等[10−11]研究了世界18个城市1km2地面街道网络,发现自组织城市的街道符合幂律分布,具有无标度性质.国内对无锡市新区整体城市道路网络进行的实证研究分析[12],发现是典型的小世界网络[13].

关于利用复杂网络理论对封闭小区开放问题进行分析的相关工作有文献[14].詹斌等使用网络节点度方差作为评价指标,基于不同策略对城市路网与小区路网进行拼接,从城市道路网络脆弱性角度比较了小区交通开放策略,发现小区路网接入节点越多,接入节点度越小,小区路网结构越复杂,城市道路网络脆弱性越低[14].

小区道路网络与城市道路网路是局部与整体的关系,但对二者进行拼接则假设它们为并列关系,因此对该问题的建模有待进一步改进.封闭小区交通开放行为对应于在道路网络中打开一些交叉口以连接小区道路与市政道路.

因此,使用对偶映射将城市道路映射为网络中的节点,交叉口映射为网络中的边,利用Barabsi-Albert(BA)模型[8]对市政道路网络建模,并验证其具有无标度特性.再根据小区的连接偏好特性加入小区道路模块,建模城市道路网络,使得封闭小区交通开放这一变化对应于在网络中添加一些边,以连接小区路网中的节点与市政路网中的节点.

本文首先对若干中国大型城市的道路网络进行实证研究,发现这些网络的度分布具有无标度性质.然后,基于复杂网络理论提出一个城市道路网络模型,使得城市道路网络包含小区道路网络.进而,考虑小区在城市中所处位置、小区的开放程度及新开交叉口所处位置等因素,制定不同的小区开放策略并应用这些开放策略对城市道路网络进行优化.然后,采用网络效率[15]作为度量指标,比较不同开放策略下网络效率的变化情况.同时,为考察网络稳定性,对开放后的城市道路网络进行攻击仿真研究,并使用Crucitti-Latora-Marchiori(CLM)模型[16]对城市道路网络在发生故障后的相继故障过程建模.最后,针对效率和稳定性这两个因子,分析城市道路网络的优化特征,并据此提出封闭小区交通开放建议.

本文的主要贡献包括:发现中国大型城市的道路网络具有无标度性质;提出一个城市道路网络模型;提出利用相继故障过程比较不同策略对城市道路网络稳定性的影响;针对效率和稳定性这两个因子,分析城市路网的优化特征.具体为:

1)发现了使用对偶表示的交通网络具有无标度特性,并基于北京、上海、广州和深圳等典型城市的真实网络数据对此做了实证研究.对北京、上海、广州及深圳等城市的道路网络进行分析,发现这些网络的度分布具有无标度性质.

2)提出一个城市道路网络模型,使得生成的网络中包含小区道路网络模块.该模型的优点包括:a)小区周围道路的统计指标(如度数)及小区内的道路数量等信息可以被方便地访问,从而在制定不同开放策略后能迅速找到符合条件的小区;b)小区内道路数量、道路拓扑结构及小区在城市中的位置可根据不同城市的小区道路情况“因地制宜”.

3)基于上述模型,提出利用相继故障过程比较不同策略对城市道路网络稳定性的影响;同时,利用网络效率比较不同策略对城市路网效率的影响.

4)针对效率和稳定性这两个因子,分析城市道路网络的优化特征,为封闭小区开放规划提供参考建议.

本文结构安排如下:第1节介绍基本定义与概念;第2节对中国大型城市道路网络的无标度特性进行实证研究;第3节给出一个包含封闭小区模块的城市道路网络模型;第4节介绍网络效率的计算;第5节阐述用于描述相继故障过程的CLM模型;第6节进行实验从网络效率及稳定性两方面比较不同小区开放策略的优劣,针对效率和稳定性这两个因子,分析城市道路网络的优化特征,最后进行收敛性分析.

1 基本定义及概念

为了便于阐述,首先给出本文将用的度、度分布、无标度网络及相继故障等概念,并对它们在道路网络中的直观意义进行解释.

1.1 度与度分布

在交通发达的城市中,道路纵横交错,在相互连接的众多道路中,存在一些连接数较多的道路,扮演着枢纽与干道的角色.对于给定的道路,与其连接的道路的数量是一个重要的统计指标.在复杂网络理论中,节点的度与网络的度分布是基本的重要概念,从不同层面反映了上述统计指标.由于使用对偶映射,即将道路映射为网络中的节点,交叉口映射为网络中的边,所以道路的连接数与城市路网中连接数的分布情况可用度与度分布描述.

对于给定的节点i的度定义为与该节点相连接的其他节点的数目,记为ki.网络中所有节点的度的平均值称为网络的节点平均度,记为hki[17].网络中节点度数的分布情况可以用分布函数P(k)来描述,表示在网络中随机选取一个节点,该节点的度数恰好为k的概率.

例如,规则格子中所有节点具有相同的度,故其度分布为δ分布,即单个尖峰.网络连接的随机化倾向会使得这个尖峰的形状变宽.极端情况为完全随机网络,其度分布近似为Poisson分布,该分布在远离峰值hki的地方呈指数下降,说明度数远大于hki的节点存在的概率很小.

但是研究表明[7,9−10,13],许多实际网络的度分布与Poisson分布显著不同,例如无标度网络的度分布符合幂律分布.

1.2 无标度网络

无标度网络的特点是不存在像完全随机网络度分布那样的平均度,使得大多数节点的度都在平均度附近.Barabsi与Albert发现无标度网络符合幂律分布[8].

其中,γ>0.因此k越大,p(k)越小,但p(k)随k的增大而下降的速度比Poisson分布的指数下降慢.这使得无标度网络中,少部分节点拥有很高的度数,大部分节点只有较低的度数.城市道路网络也具有此性质,少部分主干道连接了许多路,而大部分的非主干道只与少数道路相连.研究表明,城市的道路交通网络具有无标度特性[7,9−11].

在对数坐标系中,无标度网络将会近似为一条直线.这也是文献中常用于验证网络是否具有无标度特性的方法[18−19],在介绍城市道路网络模型时,也将以此验证市政道路网络的无标度特性.

无标度网络中大多数节点只有小度数,小部分节点拥有大度数,该特性使得网络在遭遇随机故障时具有高度鲁棒性;另一方面,这种特性使得无标度网络对蓄意攻击具有高度的脆弱性,网络中少量高度数节点发生故障会引发一系列相继故障.

1.3 相继故障

实际网络中,一个或少数几个节点或边发生的故障会通过节点之间的连接引起其他节点发生故障,产生连锁效应,最终导致相当一部分节点甚至整个网络崩溃,这种现象称为相继故障,级联失效或雪崩.

例如,在道路交通网络中,若某路段因故失效,则车辆会涌向周围的道路,当周围道路的负荷超过容量时,会形成堵塞,一旦阻塞蔓延至交叉口便会进一步扩散至与之相连的道路.如此进行下去,如果堵塞道路形成了回路,则该片区交通便瘫痪了.这带来的损失是巨大的,所以监控这种相继故障并防止其发生的意义重大.

相继故障中最初始发生故障的一个或多个节点可能是在网络中随机选定的节点,也可能恰好是网络中最重要的节点.因此在建模相继故障过程时攻击策略一般有随机攻击和蓄意攻击两种.前者在网络中随机选取节点进行攻击(使其失效),后者选取网络中较为重要的节点进行攻击,例如度最大的节点.

2 无标度特性实证研究

若要将复杂网络理论的研究方法和成果应用到城市道路网络中,首先必须说明要研究的城市道路网络具有复杂网络的特性,并对网络进行建模.

在城市道路网络的复杂网络特性实证研究中,文献[9]对美国40个城市道路网络进行了大范围的分析,发现这些道路网络都表现出小世界特性,且道路长度和度分布均具有无标度性质.Crucitti等[10−11]研究了世界18个城市1km2地面街道网络,采样4个介中性指标进行分析,发现自组织城市的街道符合幂律分布,具有无标度性质.文献[7]采用对偶法对具有不同形态和历史背景的6个城市的道路交通网络进行了拓扑分析,发现这些网络均为无标度网络[8],并且表现出小世界特性.其中,对偶法是将城市路网表示为网络的一种方法.

城市道路复杂网络研究中,路网的表示方法主要有原始法与对偶法.原始法将交叉口抽象为网络中的节点,道路抽象为网络中的边;对偶法则将道路映射为节点,交叉口映射为边.

例如,图1是一个城市道路网络的原始法表示，而其对偶法表示则如图2.注意在对偶表示方法中,可以明显地看到华穗路在这一片区所扮演的重要地位,这是对偶法的一个优点.

图1 原始法Fig.1 Primal approach

对偶法能将城市道路网络表示为更简洁的拓扑结构,易于揭示网络的特性;而且,若使用原始法表示网络,则封闭小区开放问题将转化为在网络中合并某些节点的问题,而使用对偶法,则问题简化为在网络中添加一些边.基于上述理论和实现方面的考虑,本文选择对偶法表示城市道路网络.

考虑到本文关注的封闭小区交通开放问题在北京、上海、广州及深圳等中国大型城市较为典型,选择对这几个城市进行实证研究.

借助OSMnx[22],我们获取了OpenStreet-Map[23]上这四个城市的道路网络数据(图3～6),包括每条路段的ID、类型、长度、名称以及每个节点的ID和所在经纬度.

图2 对偶法Fig.2 Dual approach

图3 北京道路网络示意图Fig.3 Road network of Beijing

在城市道路网络拓扑分析方面,原始法比较直观、易于理解,数据可以直接通过地理信息系统获得,距离度量可使用米制距离,而对偶法仅能使用拓扑距离[20].但是,应用原始法分析城市道路网络的统计性质时存在一些问题.由于城市道路网络是存在于二维地理空间的实体网络,与抽象网络不同,网络的一些特性无法通过平均路径长度、度分布等传统参数获得[21].

在这方面,对偶法优于原始法.由于对偶法中,道路被视为节点,交叉口被视为边,这使得一个节点可以拥有大量的边与其相连.事实上,一条道路可以存在很多交叉口,特别是城市中的主要道路.而若使用原始法表示,由于地理空间限制,一个交叉口很难有大量道路与其连接.因此,对偶法使得城市道路网络与其他抽象网络(节点不受地理空间限制的网络)之间具有可比性[7].

图4 上海道路网络示意图Fig.4 Road network of Shanghai

在常见的地理信息系统中,城市街道网络常常被表示为一个图,图中的边代表路段(道路的一部分),节点代表路段间的交叉口.例如,图1中的华利路被表示为三个路段.这样的图是交通建模的传统表达方式[24],但该表达不利于揭示网络中的结构和模式.从这种网络表示中去发掘网络的结构和模式就像根据图中的像素而非事物来感知一幅图(即路段之于道路网络相当于像素之于整幅图像[9]).所以,为了研究道路网络,需要将路段合并为更有意义的道路.

文献中主要的合并方法有两种:1)根据道路名,合并名字相同的路段;2)根据路段横截面,合并相邻路段中横截面相同的.

两种方法各有其优缺点,考虑到以下两个原因,我们采用方法1.

1)OpenStreetMap中的道路名信息由用户共同维护,这使得较为“活跃”的路段都有齐全的路名信息,而未命名的部分多为使用率低或地理位置偏僻的路段.

2)获取的数据集中没有路段的车道数等横截面信息,难以应用方法2.

在下文结果分析中,将进一步阐述使用这种方法对结果有什么影响.

在对偶表示法中,某个节点的度的物理意义为其对应的道路所连接的交叉口数.因此,在合并完道路后,节点的度可以通过统计道路上的交叉路口数方便地计算出来.图7～10展示了双对数坐标下,北京、上海、广州及深圳道路网络对应的度分布.

这四个城市道路网络的节点度分布在双对数坐标系下都近似呈一条直线.注意到度数为1的节点所占比例较少,对该现象进行了探索.

观察未命名的路段,发现未命名路段中存在许多连接数较低的路段(图11).这些未命名路段组成的道路在计算度数时由于名称缺失的原因未纳入计算.事实上,度数为1的道路数量应比图7～10中统计的多.考虑这一影响,可以认为这些道路网络的度分布具有无标度特性.

图5 广州道路网络示意图Fig.5 Road network of Guangzhou

图6 深圳道路网络示意图Fig.6 Road network of Shenzhen

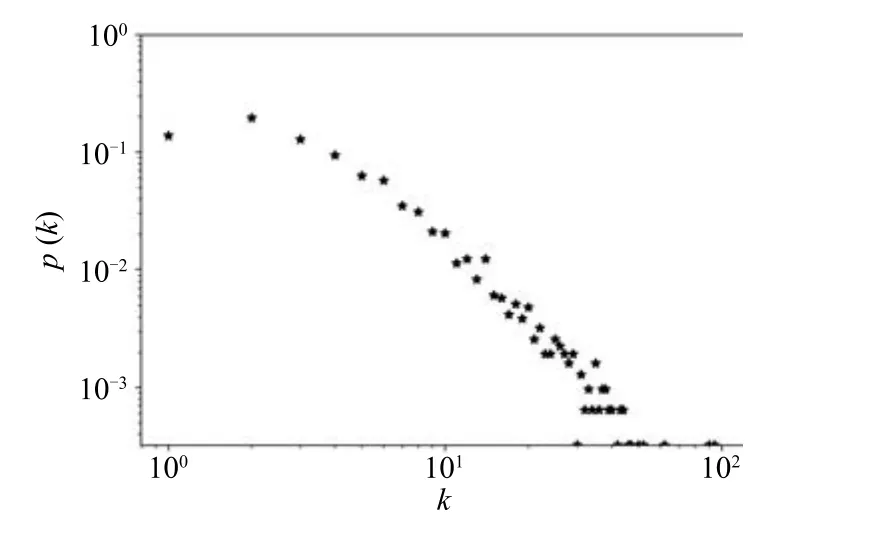
图7 北京道路网络的度分布Fig.7 Degree distribution of Beijing road network

图8 上海道路网络的度分布Fig.8 Degree distribution of Shanghai road network

图9 广州道路网络的度分布Fig.9 Degree distribution of Guangzhou road network

图10 深圳道路网络的度分布Fig.10 Degree distribution of Shenzhen road network

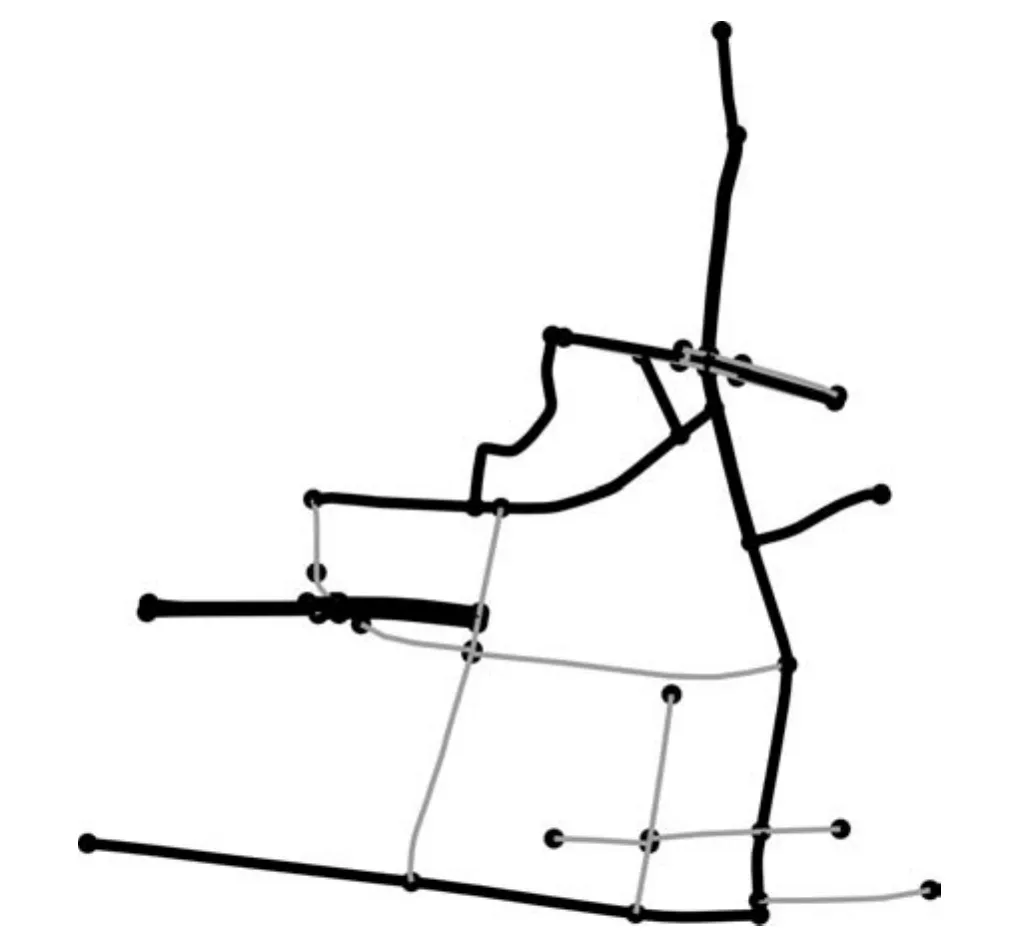
图11 道路网络图.其中,黑色线段代表已命名路段,灰色线段代表未命名路段Fig.11 The road network where black lines represent the named roads,gray lines symbolize the unnamed roads

基于城市道路网络中这种“少数道路拥有大量连接,大多数道路拥有少量连接”的特性,提出一个针对封闭小区开放及对城市道路网络进行描述的模型,该模型可表征市政道路数量的增长特性、道路及小区选址的连接偏好特性,同时便于后续对网络效率和稳定性的研究.

3 城市道路网络模型

将封闭小区交通开放对应于将网络中的小区道路网络与市政道路网络相连,这要求在生成的网络中,代表小区道路的节点与代表市政道路的节点可以被找到并连接,这是最基本的要求;在更高层面,制定不同的小区开放策略后,需要快速找到满足条件的待开放小区,这要求小区周围道路的信息(例如度数)以及小区的大小等属性可以被方便地访问;在最高层面,小区的基本属性(例如道路数量,道路连接情况,小区在城市中所处位置)应可进行适当调整,使得分析不同城市时可做到“因地制宜”.

本文提出的城市道路网络模型可满足上述要求,该模型基于以下假设:

1)市政道路增长特性.随着城市规模和社会经济活动的发展,新的市政道路不断建成.根据广州统计局相关数据资料2http://data.gzstats.gov.cn/gzStat1/chaxun/njsj.jsp,2001年广州的等级公路里程为4384km,到2014年,已经达到8121km,增长了约87.52%.

2)市政道路连接偏好特性.市政道路网络中存在一些较为重要的道路,称为“主干道”,主干道连接了较多的其他道路.为使交通更为便利,新建的道路更倾向于被连接到主干道.连接偏好特性使得模型可以描述城市路网中少数道路拥有大量连接数,而其他大量道路只拥有少量连接数.

3)小区道路网络较为规则.典型的小区路网由一两条主干道与市政道路相连,其余道路常为断头路[3],网络多为规则的网格形.

4)小区选址连接偏好特性.住宅小区、单位大院或学校在选址时,交通便利,配套设施完善的地方更易受青睐.这使得小区选址具有连接偏好特性,即连接数较多的道路上会有更多的小区,且相同功能的小区会“吸引”同类小区.

城市道路网络模型基于以上假设及BA模型[8],其具体构建步骤在模型1中给出.

模型 1.城市道路网络模型

输入.市政道路数(n1),新节点与已有节点连接数(m),小区数量(n2),小区内道路数(node).

输出.城市道路网络(GG G),小区道路网络字典(d).

模型构建的基本思想是维护一个节点列表r,若节点i的度为ki,则i在r中出现次数为ki.在生成市政道路网络阶段,新节点需要与已有节点连接时,从节点列表r中均匀地选取目标节点,如此可实现“连接偏好”特性,而不必为网络中每个节点计算且保存其被连接的概率.经验证明这样生成的市政道路网络具有无标度特性,其度分布在对数坐标下近似为一条直线(图12).

图12 1000个节点的市政道路网络度分布Fig.12 The degree distribution of municipal road network with 1000 nodes

对于小区道路网络,简单起见,在实验中假设小区只有一条主道路,但这可以容易地推广到一般情形.与主道路相连接的市政道路节点刻画了小区在城市中的位置,该节点度数较大,说明小区位于交通较为便利的中心地区,否则位于非中心地区.加入新小区时仍通过从节点列表随机选取目标节点的方式为其分配位置.但如果使用原节点列表r,小区的选址会过于集中,为解决此问题,让r中节点i出现的次数降低为,其中int(·)表示取整.这样可使网络中节点被小区连接的概率不至于相差过大.加入小区后,与该小区相连的市政道路节点在列表r中出现次数加1,使得原本小区多的地方更容易吸引新小区.

模型1中第24行是为建立一个以小区主道路为键,以相连的市政道路度数、市政道路节点索引、小区节点数,小区中其他道路节点索引组成的列表为值的字典.该字典的使用便于制定开放策略后迅速找到符合条件的小区以及小区中待开放的道路.

注意模型1第17行,不同小区中道路数目不尽相同,这可以通过从某个分布中随机生成小区道路数来建模.由于小区的道路规模大小不是本文考虑的因素,所以将其取为定值,但模型可以被方便地扩展.

这个模型对包含封闭小区路网的城市道路网络进行建模,基于该模型可研究不同的小区开放策略.执行小区开放策略会为某些节点间的通行提供“捷径”,使驾驶员不必绕路,以提升网络效率.

4 网络效率的计算

为了比较不同小区开放策略对城市道路网络效率的影响,需要定义网络效率的计算方法.

将城市道路网络建模为拥有N个节点K条边的有权无向网络G,使用一个N×N邻接矩阵{eij}描述G.如果节点i和节点j之间有边相连,则矩阵元素eij是一个属于(0,1]的值,否则eij=0.这个值可用来衡量节点i到节点j间连边的效率.例如,在交通网络中,越小的eij代表道路越拥堵,即传输效率越低.假设网络中的驾驶员都会选择效率最高的通行路线,称为(效率)最优路径.节点i与节点j间最优路径的效率被定义为路径中各段道路效率的调和平均,记为†ij.矩阵{†ij}的计算使用Johnson算法[25].对于一条具有N段道路的最优路径,其效率为

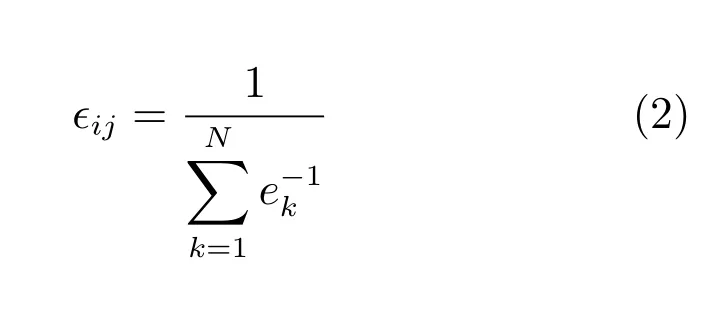
使用调和平均而不使用算术平均的原因可从一个简单例子中看出[26]:考虑与某节点相连的三条路径,第一条路径包含两段效率皆为0.5的道路;第二条路径包含三段效率都是0.5的道路;第三条路径包含两段效率分别为1,0的道路.这三条路径的效率明显不同,但算术平均都为0.5,而调和平均则分别为1/4,1/6,0.由此可见,调和平均考虑了路径中的道路数,途径道路数过多会使得效率下降;另外,若路径中存在效率为0的道路,则该路径效率为0.

为了计算网络平均效率[15],定义

注意到任意两点都直接相连的全连接网络效率最高,其最优路径的效率和为N(N−1)/2.所以,网络G的平均效率可理解为G的最优路径效率和与全连接网络的最优路径效率和之比.在比较网络稳定性时通过这样计算的网络效率,观察道路网络在发生故障后的演变情况,从而比较不同策略对城市道路网络稳定性的影响.

仅从缓解拥堵提高效率的角度进行封闭小区交通开放的探讨稍显片面.若开放后的网络能缓解平常的拥堵,而一旦遭遇局部故障便极易蔓延形成大面积交通瘫痪,即相继故障,则该开放策略也是不可取的.

5 相继故障过程的建模

为了分析不同小区开放策略对城市道路网络稳定性的影响,对网络发生故障后的相继故障过程进行建模.衡量网络稳定性亦可直接计算网络稳定性/脆弱性指标,但与之相比,对相继故障过程建模的优点在于能获得更多的差异信息.例如,网络在发生故障后演变为大面积瘫痪的临界值,相继故障过程演变的速率等.这些信息能为城市交通管理提供更大帮助.

对网络相继故障进行描述的动态模型有节点动态模型[27]、边动态模型[28]、CLM 模型[16]、二值影响模型[29]、沙堆模型[30]和OPA模型[31]等.

在这些模型中,从模型考虑对象的角度进行比较,节点动态模型只考虑了节点的故障,边动态模型只考虑了边的拥堵,二值影响模型和沙堆模型仅考虑节点的状态,而城市交通的拥堵与道路和交叉路口这两个对象都有关系,CLM模型同时考虑了节点和边的作用以及它们之间的互相作用.

从负荷确定方式的角度进行比较,节点动态模型中负荷来自外部作用,每个节点承担相同负荷,相继故障过程中不断抬高该外部作用;边动态模型的负荷由某个负荷分布指定;二值影响模型中,负荷由节点的邻居中发生故障的比例确定;沙堆模型中,先为每个节点指定“高度”(类似于负荷),在相继故障过程中每次选取一个节点抬高其负荷;对城市道路网络而言,负荷即道路的交通压力,受许多因素影响.例如,希望途径该道路的车辆的数目.若某条道路在网络中充当着“枢纽”的作用,许多车辆的最优驾驶路线都需要途径该道路,那么这条道路的车流量常常较大;又如,道路前一刻的交通压力.某片区拥堵后,后继的驾驶员通过电台等途径了解到该片区拥堵,则会选择绕行,从而减轻该片区的交通压力.CLM模型中,节点的负荷由途径该节点的最优路径条数确定,这描述了上述影响交通压力的一个因素;节点发生故障后,CLM模型会降低与其连接的边的传输效率,使得该节点及周围节点不易成为最优路径的选择,从而减小了负荷,这样的更新机制类似于上述影响交通压力的另一个因素.

从承载力确定方式的角度进行比较,节点动态模型中,节点承载力由Weibull分布确定;边动态模型的边承载力指定为1;二值影响模型与沙堆模型中的节点阈值(承载力)均为直接指定的.城市道路的承载力与设计通行能力有关,若某道路被设计承担较大的通行压力,则其承载力会较大.CLM模型中,节点的承载力与初始负荷成正比.

从模型对故障单元处理方式的角度进行比较,节点动态模型直接去除故障节点;边动态模型对故障边的负荷进行分配或直接丢弃;二值影响模型将节点的状态改为故障;沙堆模型对故障节点执行“倾倒”操作,即分配其负荷到邻居节点.事实上,对于道路网络,工作状态不佳的道路很少会被直接移除,拥堵路段的通行状况会在高峰期后慢慢恢复正常状态.CLM模型对故障节点的处理方式为降低与其连接的边的效率,这会使得途径该节点的最优路径数下降,从而使节点缓慢恢复正常状态.

综上比较,在本文研究的应用背景下,选择CLM 模型对网络相继故障过程进行建模较为合适.

CLM模型中,首先将所有边的效率初始化为1

定义t时刻节点i的负荷为通过它的效率最优路径的条数,并记为Li(t),其中效率最优路径的定义与第3节的定义一致.定义t时刻节点i的容量为[15]

其中,α是一个容许参数,大于等于1且不会过大,现实意义为:设计道路网络时,首先须保证道路正常运行;其次,可投入于道路建设的资金是有限的,所以道路的容量不能无止境地大.这样设定节点的负荷与容量保证最开始所有道路都正常工作,然后移除网络的一个节点,使一些节点对之间的效率最优路径发生变化,导致某些节点上的负荷增加,以至于可能超过其容量,从而导致无法正常工作,降低周围边的效率.具体效率更新公式为

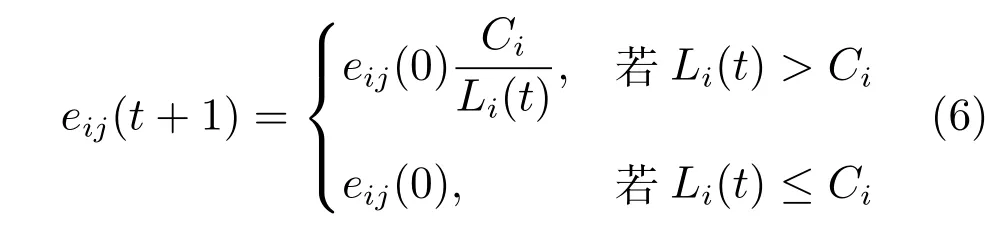
其中,eij(t)表示t时刻与节点i相连的道路的效率.该公式的意义为:若某节点的负荷超过其容量,则降低与之相连的边的效率,且过载程度越严重,降低程度越大;否则保持初始效率.

在道路网络中,若某道路严重堵塞,堵塞的车辆蔓延到交叉口,则交叉口的通行效率会降低,进而使得驾驶员会选择其他的道路,这对应于网络中效率最优路径的变化.

这种降低过载节点效率的处理方式与直接移除过载节点的方式[32]相比,更为适合描述城市道路网络的相继故障过程,因为城市道路很少由于过载而被移除.使用CLM 模型建模相继故障过程的具体步骤见模型2.

模型 2.相继故障过程

输入.城市道路网络(G),容许参数(α),最多迭代次数(iter).

输出.相继故障过程中网络效率变化情况.

6 实验与结果

为了定量分析不同小区开放策略对城市道路网络效率及稳定性的影响,利用模型1构建城市道路网络,对开放后的网络计算网络效率和对相继故障过程建模.实验环境为Intel Core i5-4210M 2.60GHz,内存8GB,Ubuntu操作系统,编程语言为Python2.7,实验过程利用了NetworkX[33].

6.1 构建城市道路网络模型

在对城市道路网络的无标度特性进行实证研究时,使用真实的道路网络数据,但该数据(包括其他已有数据)的精度和信息量不足以用于验证本文提出的模型.现有的基于真实数据的研究[3]使用的都是局部的调查数据,不适用于本文的宏观建模分析.这些真实网络数据存在以下问题:

1)道路类型数据不完整.许多道路(特别是我们感兴趣的小区道路)类型属性为unclassified,无法辨别.而利用道路网络研究封闭小区开放问题的基本要求是代表小区道路的节点和代表市政道路的节点可以被找到并连接.道路的类型属性缺失使得这一基本要求得不到满足.

2)封闭小区信息缺失.哪些道路属于同一小区是未知的.而在制定不同的小区开放策略后,需要找出满足条件的待开放小区.这要求小区内及小区周围的道路信息可以被查询并存储.但小区信息的缺失使得这一要求不被满足.

3)小区开放后的交通数据信息也是未知的,无法直接验证开放的效果,对此只能进行仿真研究.

考虑到封闭小区在上海占总居住小区的83%,广东省的封闭小区覆盖了70%以上的城乡面积[2].设定城市道路网络中拥有1000个市政道路节点(在所获数据集中深圳市道路节点数为1276)与460个节点数为5的小区,这样小区道路数约占总道路数70%,若有具体的小区道路数与市政道路数,该参数可以设置得更精确.为验证市政道路网络具有无标度特性,图12给出了在对数坐标下的度分布,该分布图形近似为一条直线.考虑到一条市政道路一般至少会在道路两端各连接另外一条道路,参数m被设为2,即生成市政道路网络时每个新节点会与两个已有节点相连.

6.2 封闭小区交通开放策略

制定封闭小区开放策略时,考虑以下三个因素:小区在城市中所处位置、交通开放的程度以及新开的交叉口位置.

小区在城市中所处位置是推行差异化开放时应考虑的因素,处于不同位置的小区在交通开放后给城市道路网络带来的正面及负面影响不尽相同.例如,在较为繁华、容易堵塞的地段开放封闭小区,一方面,驾驶员可以选择利用小区内道路避开拥堵路段,缓解拥堵的恶化;另一方面,开放小区后网络的可达性提高了,车辆可以更方便地到达这些拥堵地段,更多的车辆涌向“拥堵重灾区”可能进一步加重拥堵情况.而在远离中心,交通不那么发达的地区开放封闭小区,一方面,可以使得市民出行有更多路线甚至捷径选择,无须依赖主干道,从而缓解主干道负担;另一方面,可能对城市中心地段的拥堵情况没有太大改善.

为体现小区位置带来的差异,以连接小区主道路的市政道路的度数为筛选条件,选择符合条件的待开放小区.具体地,以中位数为临界值,若连接小区主道路的市政道路度数大于所有道路度数的中位数,则称该小区为中心地段小区,否则称为非中心地段小区.

此外,在众多热议中,小区居民对政策执行最大的质疑在于此举可能侵犯小区业主共有权益,例如道路、绿地以及公共场所等[4].对于城市交通而言,一般开通部分道路便可打通封闭小区堵塞的“毛细血管”,而不必开通所有道路.若开通部分道路对城市道路网络效率及稳定性的提升与开通所有道路相当,甚至更优,则从考虑小区业主意见,工程费用的角度来看,只开通封闭小区中的部分道路是更优的.为此,在开放封闭小区时,设置了半开放或全开放策略,区别是在小区内选择不同数量的道路与市政道路相连.若选择半开放策略,则在小区中均匀随机选定一半道路作为开放道路.

最后,小区道路与市政道路如何连接也是备受关注的问题[4],新开交叉口的位置需要谨慎选择,否则会带来一些不良影响.例如在车流量较大的道路新开交叉口可能增加交叉口的冲突数及延误[34].我们找出与小区主道路连接的市政道路,对其邻接节点以及邻接节点的邻接节点取交集得到小区周围的道路集合S.以S中道路度数的中位数为界,称度数大于中位数的道路为繁忙道路,小于中位数的为清闲道路.对于交叉口位置的选定,制定繁忙交叉口策略与清闲交叉口策略.若选择繁忙交叉口策略,则待连接的市政道路在繁忙道路集中随机选择;选择清闲交叉口策略则在清闲道路集中选择.表1给出了根据上述三个因素制定的所有可能策略.

6.3 网络效率比较

首先,根据表1中的策略对原始网络进行小区交通开放优化,得到8个不同的开放后城市道路网络.然后,使用第3节定义的网络效率,分别对开放后的城市道路网络进行网络效率计算.

表1 不同的小区开放策略Table 1 Different community opening strategies

在网络生成、待开放道路及新开交叉口位置选择过程中存在一定随机性,该随机性会对实验结果造成影响.为消除这些随机因素带来的影响,我们进行了多次实验.最终得到图13的比较结果.

图13 不同开放策略优化后的城市道路网络效率对比Fig.13 The comparison of the efficiency of urban road networks optimized by different opening strategies

从图13可以看出,由E,F,G,H开放策略优化过的城市道路网络效率较原始网络有提高,而策略A,B,C,D则无明显区别.从表1可以看出,效率有明显提高的策略具有共同的特点,即选择了位于非中心地区的小区,其中又以策略E优化的网络效率最优,该策略选择非中心地区的小区进行交通开放,对小区内道路采取完全开放的策略,新开的交叉口选择在连接数较多的繁忙道路.网络效率提高程度次优的是策略G,与E策略唯一不同的是小区内道路采取部分开放的策略,比较其他仅由开放程度不同带来的差异,发现从提高网络效率的角度,在待开放小区和新开交叉口不变的情形下,小区内开放的道路越多效率越高.效率提升程度第三的F策略与E策略相比,差异仅在交叉路口位置的选择,对比其他仅由交叉口位置不同带来的区别,发现选择了繁忙交叉口的策略皆稍优于选择了清闲交叉口的策略.

对多次实验结果求平均,整理为表2,从网络效率最优的角度来看,开放策略E是较为理想的.但是对城市道路网络的优化不能仅以效率为优化目标,一个高效而不稳定的网络是不可取的,下面从网络稳定性的角度研究不同的开放策略.

6.4 网络稳定性比较

研究网络稳定性时,我们希望比较不同开放策略优化后的城市道路网络在重要道路出现故障(例如路面坍塌、严重事故等)时展现的抵抗能力.为此,对优化后的城市道路网络进行蓄意攻击:移除网络中度数最高的节点.此举会导致网络中一些效率最优路径发生改变,从而使得某些节点上效率最优路径条数增加,以至于其负荷超过容量,进而降低周围边的效率,再次改变效率最优路径,使得道路故障的影响向外扩散,最终降低网络平均效率.在复杂网络相继故障的研究中,一般采用随机攻击与蓄意攻击两种策略.由于生成的城市道路网络对随机攻击具有一定的鲁棒性,只要容许参数α不至于过小,网络效率一般变化不大(图14),这样难以比较不同的小区开放策略对城市道路网络稳定性的影响,所以选择蓄意攻击策略.

对于容许参数α的选定,如果设定太高,由节点失效引发的相继故障过程不会出现,网络效率会几乎保持不变;若α设定得很接近1,相继故障过程会发生且网络效率剧烈下降,很快便崩溃了;而适中的α值会使得相继故障过程缓慢发生,最后网络效率稳定某个于值.观察发现网络通常在10～20步间重新达到稳定状态[26].为观察不同小区交通开放策略对网络稳定性的影响,我们通过多次实验选取适中的值α=1.8以观察网络的节点失效后的相继故障过程,详见图15.

从图15可以看出.使得网络效率最高的开放策略E在稳定性方面的表现几乎是最差的.虽然一开始其效率远高于使用其他策略的网络,但在节点发生故障后,网络效率剧烈下降,在第5步时便稳定在其最低效率的位置.此外,对比第1步的下降程度可以发现,使用策略E的网络在节点失效后的相继故障过程突发性极强,几乎没有征兆,这对于城市道路网络十分不利,若发生大面积瘫痪前的变化较为缓和,交通管理部门可结合智慧交通[35]捕捉前兆,及时对拥堵进行疏导缓解,防止情况进一步恶化.

表2 不同开放策略优化后网络的效率对比Table 2 The comparison of the efficiency among networks optimized by different strategies

图14 随机攻击策略下网络相继故障过程Fig.14 The cascade failure of network under random removal

图15 不同开放策略优化后城市道路网络的相继故障过程Fig.15 The cascade failure of rural road networks optimized by different opening strategies

策略F虽然在效率方面稍差于策略E,但在网络稳定性方面的表现却是最优的.在节点失效后,网络效率先呈缓慢下降,再加速下降,而在第1步到第9步其表现一直优于其他网络,与其他网络(例如E策略与G策略)的断崖式下降相比,策略F对应的网络效率下降缓慢温和,在将近第10步才下降到其最低位置,而策略G仅在第5步便处于该水平了.

此外,明显能提高网络稳定性的策略还有H.虽然其在效率和稳定性的提升上都不如策略F,但这样的开放策略在效率和稳定性两方面都有相对于原网络的提高.

策略A,B,C,D的曲线很大部分都与原网络代表的曲线重合了,有些表现甚至比原网络差.这些策略的共同点是都选择了中心地区的小区,说明开放周围道路连接数较多的小区,会使得网络稳定性下降.原因是此类开放策略增加了网络中的重要节点,一旦重要节点失效,则容易造成严重的相继故障.在现实道路网络中,开放繁忙地区的封闭小区使得该区域的交通可达性提高,车辆可以更方便地到达繁忙地区,使其负荷增加,而一旦发生故障,大量车辆涌向周围道路.例如,刚开放的小区道路,由于这些道路设计时未考虑如此大的负荷,容易造成进一步的道路故障,如此层层影响.

6.5 网络关于效率及稳定性的优化特征

由于使得网络效率最高的策略在网络稳定性方面表现最差,故在制定封闭小区交通开放策略时,需权衡这方面因素,找到最优的方案.

若为网络稳定性选择了某种度量指标S,并记候选策略中稳定性最优的网络对应的稳定性度量指标值为S∗.同样地,将效率最优的网络对应的网络效率记为E∗.于是,策略i优化后网络的综合评价可表示为

其中,Gi为经策略i优化后的网络,β为重要性参数.β越高代表越重视道路网络的效率,反之则重视道路网络的稳定性.

在制定封闭小区交通开放策略时,可以收集城市道路数据,使用第2节的城市道路网络模型建模城市路网,选定度量网络效率及稳定性的指标后,结合式(7)选择候选策略中的最优策略.

6.6 收敛性分析

上述实验过程中存在一些可能影响结果的随机因素,如生成城市道路网络时,连接节点的选择具有随机性,小区中待开放道路及其新开交叉口的位置的选取都存在一定的随机性.为保证实验结果的参考价值,进行了多次实验,并取其均值.

图16展示了该均值随试验次数的变化情况.9个子图分别描述了8种不同开放策略优化后的网络与原网络的收敛情况.结果表明,该均值在一定实验次数后趋于稳定,因此随机因素不会过分影响实验结果.

图16 多次实验结果的均值收敛到某一值Fig.16 The mean of the experimental results converges to a certain value

7 总结与展望

本文首先对若干中国大型城市的道路网络进行实证研究,发现这些网络的度分布具有无标度性质.然后,基于复杂网络理论提出一个描述城市道路网络的模型,该模型适用于封闭小区的开放问题.与拼接城市道路网络和小区路网的已有做法相比,该模型使得城市道路网络包含了小区道路网络,且道路信息易于查询与筛选,这有利于制定与比较不同的小区开放策略.基于该模型,从网络效率及稳定性的角度研究了不同封闭小区开放策略的优劣.其中,开放策略考虑的因素有小区在城市中的位置、小区开放程度及新开交叉口的位置.结果表明,封闭小区应该开放,且开放位于非中心地段的小区,小区内道路完全开放,新开交叉口位于连接数较低的道路时,网络的效率及稳定性综合提升最优.

由于该问题较新,相关数据缺乏,本文模型中参数的设定有待进一步改善.将来可通过收集某城市市政道路数、小区数量及小区道路数,更精准地对城市道路网络建模.此外,以后的工作中,在统计道路节点度分布前进行路段合并时,若能获取道路横截面信息,结合两种路段合并方法更佳.