具有总能耗约束的柔性作业车间调度问题研究
2018-12-05雷德明杨冬婧
雷德明 杨冬婧
柔性作业车间调度问题(Flexible job shop scheduling problem,FJSP)广泛存在于汽车装配、纺织、化工生产和半导体制造等制造过程和行业中,自Bruker等在1990年的开创性工作[1]之后,FJSP的研究受到广泛关注,取得了很大进展[1−27].
由于FJSP的高度复杂性,精确算法难以在合理的时间内对其求解,使得智能算法成为解决FJSP的主要手段,智能算法已成功应用于各类FJSP的求解,其中关于多目标FJSP,早期的工作为Kacem等[2]提出的基于遗传算法和局部方法的混合算法,在此之后,研究者大量应用GA(Genetic algorithm)[2−9]、粒子群算法[10−11]、和声搜索算法[12]、人工蜂群算法[13]、禁忌搜索[14−15]、变邻域搜索[16]、蛙跳算法[17]和分布估计算法[18]等求解FJSP.
近些年,低碳制造和低碳生产调度受到工业界和学术界的广泛关注,其中关于低碳FJSP,Tang等[19]考虑了FJSP的能耗并运用遗传模拟退火算法求解.Liu等[20]运用GA求解双目标低碳FJSP.He等[21]提出一种节能优化算法,它通过机床选择减少机器加工能耗和操作序列调整减少机器闲置时的能源浪费.Zhang等[22]设计结合改进局部搜索的多目标GA以解决低碳FJSP.蒋增强等[23]提出了基于血缘变异的改进非劣排序遗传算法(Non-dominated sorting genetic algorithm-II,NSGA-II[28]).唐立力[24]给出一种改进型候鸟优化算法.Yin等[25]运用多目标GA解决了具有产能、能源效率和噪声减少等目标的FJSP.文献[26−27]分别利用一种新型蛙跳算法和一种新的教学优化算法求解低碳FJSP.
尽管低碳FJSP的研究取得了较大进展,但其研究仍不够深入,有些问题的研究还未引起研究者的重视,例如,具有总能耗约束的FJSP,在该问题中,总能耗不是目标函数,无需最优化,总能耗只需不超过给定的阈值即可,能耗约束的加入,产生了如下几个新特征:1)总能耗约束不是总能得到满足,即智能算法的解所具有的总能耗经常超过给定的阈值.2)总能耗与机器分配和工件加工顺序密切相关,其阈值难以事先确定.3)由于以上两个特点,需要利用新原理和策略比较问题的解并更新非劣解集.
如上所述,多种智能算法在FJSP和低碳FJSP方面都具有成功的应用,不过,作为一种模拟社会政治行为的帝国竞争算法(Imperialist competitive algorithm,ICA)[29],尽管已在设备布局[30−31]、调度[32−37]、装配线平衡[38−40]、旅行商问题[41]等方面具有一些成果,但ICA较少用于FJSP和低碳FJSP的求解[36−37].根据文献[29],ICA既具有较强的邻域搜索能力,又是有效的全局优化方法,且结构灵活,这些特点表明ICA在求解FJSP和低碳FJSP方面具有不同其他算法如GA的优势,如不必像GA那样要加强局部搜索才能实现全局搜索与局部搜索的协调,因此,有必要研究ICA在FJSP和低碳FJSP方面的应用.
本文研究具有总能耗约束的FJSP,由于该问题的能耗约束经常无法得到满足,为了有效地解决问题,首先将问题转化所有约束都可满足的三目标FJSP,以简化对能耗约束的处理,同时扩大搜索区域,然后直接优化原问题,以进一步改进第一阶段的搜索结果,为此,设计基于ICA和VNS(Variable neighborhood search)的双阶段算法,先应用ICA产生一定数量的可行解,然后运用VNS对可行解改进,其中,ICA不直接求解原问题,而是优化具有总能耗、总延迟时间和Makespan的三目标FJSP;而VNS则从第一阶段获得的解出发,对原问题求解,并通过周期性更新当前解增强VNS的探索能力和它本身较强的局部搜索能力,不断提高解的质量.通过大量仿真实验,验证所得阈值的合理性和算法的搜索性能.
1 问题描述
具有能耗约束的FJSP描述如下:存在工件集J={J1,J2,···,Jn}和机器集M={M1,M2,···,Mm}.工件Ji具有hi道工序,工序oij为工件Ji的第j道工序,该工序可由相容机器集Sij中的任何一台机器加工,Sij⊂M.机器Mk具有两种模式:加工模式和空闲模式.Ek,SEk分别表示机器Mk在加工模式和空闲模式时单位时间的能耗.
存在一些与机器和工件相关的约束,包括同一时刻一台机器最多只加工一道工序,同一时刻一个工件最多只能在一台机器上加工,工序加工不能中断准备时间和清理时间包含在加工时间内等.
另外,还考虑总能耗约束TEC≤QEC,式中,

其中,TEC表示总能耗,yijk(t)为二进制量,如果在时刻t机器Mk∈Sij处于加工模式,则yijk(t)=1;否则,yijk(t)=0;如果机器Mk在时刻t处于空闲,则zk(t)=1;否则,zk(t)=0.QEC为总能耗阈值.Cmax表示最大完成时间.
问题包括调度子问题和机器分配子问题.问题的目的在于在所有约束满足的条件下同时最小化如下两个目标函数.
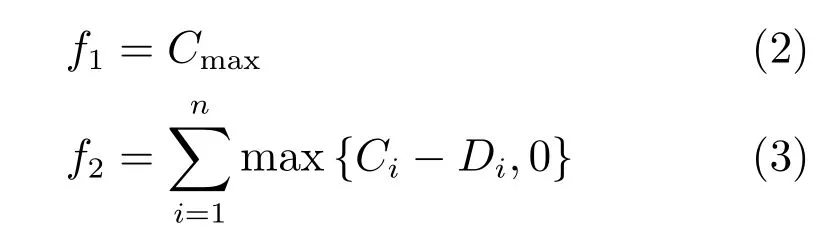
其中,Ci,Di表示工件Ji的完成时间和交货期,目标函数f1,f2分别为Makespan和总延迟时间.
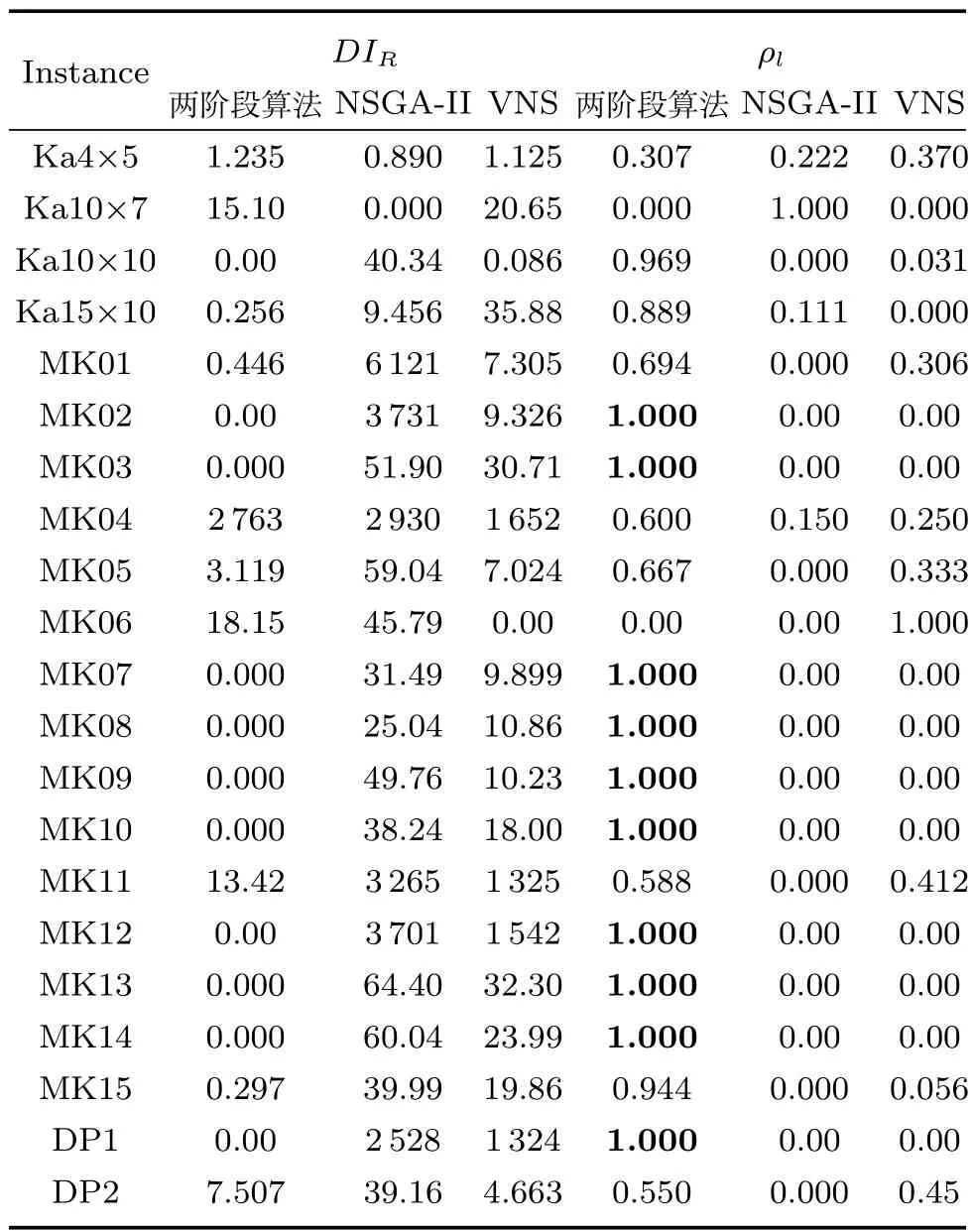
对于多目标优化问题,假设其目标总数为G且都是最小化目标,其最优解不再只是单独一个解,而是一组解的集合,且需要通过比较所有解才能确定最优解集.通常,要用到如下几个概念:对于解x,y,如果对于∀i∈{1,2,···,G},fi(x)≤fi(y);且∃i∈{1,2,···,G},fi(x) 对于所研究的FJSP,需要确定合适的能耗阈值,同时在所有约束条件满足的情况下,最优化两个目标函数,为了完成这两个任务,提出一种基于ICA和VNS的双阶段算法. 针对具有n个工件和m台机器的FJSP,通常利用调度串 [(θ1,r1),(θ2,r2),···,(θi,ri),···,(θh,rh)]和机器分配串 [q11,q12,···,q1h1,···,qnhn]来表示问题的一个解,其中,表示工序总数. 在第一个串中,θi∈{1,2,···,n},1≤ri≤hθi,二元组(θi,ri)对应工序oθiri,这样整个串对应一个有序工序表 [oθ1r1,oθ2r2,···,oθiri,···,oθhrh].第二个串中,基因qij∈Sij表示用于加工工序oij的相容机器.上述编码方法[27,41]能保证除总能耗约束TEC≤QEC之外的其他约束总是成立,但无法保证能耗约束总是成立.对于新加入的约束TEC≤QEC,需要确定阈值QEC并处理不可行解. 本阶段首先将能耗约束从原问题中去掉,而增加第三个目标f3=TEC,这样问题变成具有f1,f2,f3的FJSP,通过问题的转化,将原问题转化为所有约束都可以得到满足的问题;然后,设计一种新的ICA对三目标FJSP进行求解;最后,根据ICA的结果确定合适的阈值.由于原问题的不可行解是转化后问题的可行解,这样扩大了ICA的搜索区域,有助于获得高质量的解. ICA的主要步骤包括构建初始帝国、殖民地同化、殖民地革命、交换和帝国竞争,本文根据转化后的FJSP的特点,采用一些新策略实现ICA的以上步骤,构建新的ICA. 由于只增加一个目标,只在第一阶段优化三目标FJSP,ICA的非劣排序复杂性将有所增加,但非劣排序不是每代都做,故问题转化对算法复杂度的影响不大. 2.2.1 初始帝国构建 由于所研究FJSP的多目标特性,导致种群中的优秀个体经常彼此非劣,当这些个体被选作殖民国家时,应该分配相近数量的殖民地以同等对待它们.基于该思想,提出了一种初始帝国构造新方法.假设初始帝国总数为Nim,种群规模为N,显然,殖民地总数Nc=N−Nim,其具体过程如下: 步骤1.对初始种群P中的解按文献[28]的方法进行非劣排序,得到每个解的rank值. 步骤2.确定rank值为1的η个解. 步骤3.如果η 步骤4.对于每个帝国k=1,2,···,Nim,如果k 其中,round(z)为最接近z的整数. 当η 2.2.2 同化与革命 同化和革命是ICA的重要步骤,本文提出了革命的实现新途径.对于调度问题,同化往往通过利用殖民地和殖民国家之间的交叉[32−37]来实现. 本文的同化过程如下:对于帝国内的殖民地λ和殖民国家v,随机产生一个随机数s,如果s<ζ,则对两个解的调度串应用第一种交叉;否则,对两个解的机器分配串应用第二种交叉,产生新解z,并与殖民地λ进行比较,若新解支配殖民地λ或者与殖民地λ彼此非劣,则利用新解替代殖民地λ,并更新非劣解集Ω,其中两种交叉的详细过程见文献[26−27]. 通常,调度子问题比机器分配子问题更复杂,求解难度更大,为此,令ζ>0.5以分配更多的计算资源给调度子问题,通过实验确定,ζ=0.6. 非劣解集Ω的更新过程如下:将新解加入到集合Ω之后,对集合内的所有解进行Pareto比较,保留非劣解,剔除受支配解.以上更新过程是根据三个目标f1,f2,f3对解进行比较,而不是原问题中的f1,f2. 殖民地革命模拟某种非预期的改变,例如,改变殖民地的语言或宗教,从而改变其特征和地位[29].本文采用新的策略实现殖民地革命,其具体过程描述如下: 对于帝国k 步骤1.令α←1,对于每个τ=1,2,···,Fk,产生随机数rand,若rand 步骤2.根据Pareto支配对帝国内的所有殖民地进行比较,确定每个殖民地λ的wλ. 步骤3.若α>1,则对于l=1,2,···,α,执行如下步骤: 确定具有最小wλ的殖民地λ,令g←1 重复执行如下步骤R次: 若g=1,则对殖民地λ执行insert;否则,对殖民地λ执行change,产生新解z; 若新解支配殖民地λ或者与殖民地λ彼此非劣,则利用新解替代殖民地λ并更新集合Ω;否则g←g+1,若g=3则g←1. 其中,R为整数,UR表示革命概率. 关于革命概率UR,文献[42−43]分别将其设置为0.35和0.3.与文献[42−43]不同,只有部分相对优秀的殖民地参与革命过程,基于这一特征,本文选择一个较小的UR,根据实验确定UR为0.1. 3、外文字母的大、小写和正斜体要分清,希腊文要写清并注明;符号上下角的高低位置应明确区别,例如;凡国内尚未用过的译名,请在译名后附原文,外国人名及企业名称直接用外文,不要译成中文。 对于帝国内殖民地,如果殖民地λ受同一帝国的其他wλ个殖民地支配,则该殖民地赋给值wλ.只有wλ值最小的部分殖民地参与革命,这是因为利用较优秀的殖民地更容易获得更好的殖民地,甚至产生新的殖民国家. 由于FJSP具有两个子问题,为此,运用多种邻域结构insert,swap和change产生新解,其中,insert将随机选择的调度串元素(θi,ri)插入到新位置k 6=i并随后根据θi在调度串中出现的次序为ri重新赋值[26].swap则在互换调度串的两个不同元素之后为ri重新赋值.change的实现过程如下:首先构建集合Θ={qij||Sij|>1,i=1,2,···,n,j=1,2,···,hi},然后从集合中随机选择一些元素,为它们重新赋值,例如,qij被选中,则从Sij中随机确定一台机器替代当前的qij. 2.2.3 帝国竞争 帝国竞争是ICA的重要步骤.对于本阶段考虑的三目标FJSP,给出了一种新方式来计算一个解的成本(cost),成本值主要根据解的rank值和拥挤距离来确定,为此,首先通过非劣排序[28]将种群分解成rankmax个Hl,其中,Hl内元素的rank值均为l;然后,对每个集合Hl的非边界解,按文献[28]的方法计算拥挤距离,得到这些距离的最大值ψ,边界解的拥挤距离为ψ+α,其中,α≥1,利用α是为了区分边界解与其他解. 帝国竞争的新过程描述如下:如果Nim≥2 步骤1.确定种群P内所有解的rank值和拥挤距离. 步骤2.对于集合Hl,l=1,2,···,rankmax,将该集合内解的成本定义为,其中,distf表示个体f∈Hl的拥挤距离. 步骤3.按照基本ICA[29]的过程实现帝国竞争的剩余步骤. 计算帝国总成本时的参数ζ仍取0.1. 2.2.4 ICA描述 ICA的具体过程如下: 步骤1.随机产生初始种群并确定初始集合Ω. 步骤2.殖民地同化与革命. 步骤3.殖民地与殖民国家之间的交换. 步骤4.帝国竞争. 步骤5.如果第一阶段的终止条件成立,则停止搜索;否则转到步骤2. 其中交换过程如下:对于帝国内的每个殖民地,确定殖民地能否支配殖民国家或者与殖民国家彼此非劣,是,则利用殖民地替代当前殖民国家,成为帝国新的殖民国家,而原殖民国家则变成殖民地. 第一阶段终止条件为目标函数估计次数,由于步骤2每次循环产生的解个数不一样,在步骤2执行过程中,要判断终止条件是否成立,成立则停止搜索. 总之,ICA根据所研究FJSP具有多目标、双子问题和调度子问题更复杂等特点,构建初始帝国、让优秀殖民地参加革命、同化过程偏重于调度子问题的优化以及结合rank值和拥挤距离进行帝国竞争,这些策略与问题特点相适应,有助于提高ICA的求解质量. 2.2.5 总能耗阈值 文献[44]考虑了能耗阈值QEC,但并未讨论如何确定阈值大小.本文根据第一阶段ICA的优化结果来确定阈值,这样可以减少决策者的认知和决策负担. 关于每个实例,获得QEC的具体过程如下: 步骤1.ICA随机运行20次; 步骤2.计算Qi=max{TEC(z)|z∈Ωi},; 步骤3.从所有满足Qi≥的Qi中剔除一些相近的Qi; 步骤4.运行两阶段算法并根据计算结果确定哪个Qi≥¯Q可以作为QEC. 其中,Ωi表示ICA第i次运行所获得的非劣解集. 本阶段利用VNS求解具有TEC≤QEC的FJS-P,由于总能耗约束不总是得到满足,需要处理不可行解,为此,给出一种新原则来比较两个解x,z: 1)TEC(x)>QEC和TEC(z)≤QEC; 2)x,z都是可行解,且z不受x支配; 3)x,z都是不可行解,且TEC(z)≤TEC(x). 以上三个条件只要有一个满足,则解x被z替代,其中条件(2)根据f1,f2对两个解进行Pareto比较. 关于集合Ω,第一阶段它由通过比较f1,f2,f3而得到的非劣解组成,在从第一阶段过渡到第二阶段,该集合被直接保留下来,这样,导致Ω中存在一些不可行解. 第二阶段集合Ω的更新过程如下:对于解x 1)若TEC(x)>QEC 如果集合Ω中至少存在一个不可行解y,且满足TEC(x) 2)若TEC(x)≤QEC 如果集合Ω所有解都可行,则存在两种情况. a)解x与Ω中的一个成员具有相同的f1,f2,但x的总能耗更小,则利用x替代该成员. b)情况1的条件不成立,则直接将x添加到集合Ω中,对所有解根据f1,f2进行Pareto比较,剔除所有受支配解. 如果集合Ω中存在不可行解,则直接用x替代其中一个不可行解. VNS的详细步骤如下: 步骤1.将集合Ω中的第一个解当作当前解,令w←max_it1. 步骤2.令g←1. 步骤3.重复如下步骤直到g=3或w>max-it随机产生解z∈Ng(x). 根据上述原则,如果x能被z所替代,则直接替代,并利用新的x更新集合Ω且g←1;否则,g←g+1. 如果w能被整数β整除,则选择y∈Ω并替代x. 步骤4.如果w≤max-it,则转到步骤2;否则,停止搜索,剔除Ω中的非可行解. 其中,max-it1为第一阶段的终止条件,max-it为整个两阶段算法的终止条件,N1,N2,N3分别表示邻域结构swap,insert,change,Ng(x)表示运用Ng所产生的x的邻域解集. 集合Ω更新过程中,每次最多只剔除一个非可行解,是为了使Ω中保留足够多的解,以便在重新选择当前解时有更多的可能性. 如上所述,运用两阶段算法可以简化对能耗约束的处理,扩大ICA的搜索区域,从而提高搜索质量. 另外,它还具有如下特点:它不仅能求解所考虑的FJSP,而且能获得合适的总能耗阈值;它将全局搜索算法和局部搜索算法有机地结合在一起. 为了测试两阶段算法在求解具有总能耗约束的FJSP方面的性能,利用37个实例MK1-15[45]、DP1-18[46]、Ka4×5、Ka10×7、Ka10×10、Ka15×10[2]进行计算实验,这些实验由Microsoft Visual C++6.0编程实现,并运行于4.0GB RAM 1.70GHz CPU PC. 为了用于所研究的FJSP,在37个实例中引入能耗信息:Ek∈[2,4],SEk=1,其交货期计算公式如下: 其中,δ的值如表1所示. 表1 δ的设置Table 1 The setting onδ 其中,σxy表示解x与参考解y在归一化目标空间中的距离, 选用NSGA-II[8]和VNS[16]作为对比算法,这两种算法对FJSP具有较多的应用[5,8,16,23],且很容易应用于所研究的FJSP的求解.NSGA-II作为求解多目标优化问题的著名算法,其主要步骤包括非劣排序和拥挤距离的计算等.文献[8]针对具有随机故障的FJSP,应用NSGA-II求解,为了应用于具有总能耗约束的FJSP,对该算法做如下修改:去掉与随机故障相关的部分,对可行解采用算法原来的非劣排序和拥挤距离计算,所有不可行解赋予同样的且大于可行解最大rank值的rank值,拥挤距离设置为ωmax−TEC(x),其中,ωmax为足够大的正数. 文献[16]所设计的VNS用来解决具有加权目标的FJSP,将第2.3节中新旧解更替原则和非劣解集更新策略引入后,该VNS可直接求解本文所研究的FJSP,但该VNS与两阶段算法中的VNS的邻域结构和算法结构不一样. 两阶段算法的参数设置如下:N=80,Nim=6,max_it1=20000,max-it关于Ka4×5为2.5×104,关于其他实例为105,β关于Ka4×5为4000,关于其他实例为5000,R=8. NSGA-II的参数如下:种群规模为100,交叉概率为0.8,变异概率为0.1,最大代数为max_it/100.这些参数值根据计算实验而得,是使算法获得最佳结果的一组值. 关于 VNS,nmax=350由文献 [16]给出,max-it与两阶段算法相同. 关于总能耗阈值QEC,如果阈值过大,大多数解都满足总能耗约束,这样的阈值没有意义;如果阈值过小,则算法很难得到可行解,导致整个算法的优化只是处理能耗约束,目标函数难以得到充分的优化,故需要设置一个合适的阈值. 第2.2节给出了确定阈值的详细过程,以Ka10×7为例,随机运行ICA20次,得到20个Qi,如表2所示,等于229.7;然后,对于大于的Qi,剔除230.2,232.4,244.4,254.1等相近的值,得到剩余的Qi;最后,运行整个两阶段算法,分别测试剩余的Qi,根据上述两种指标评价计算结果,最终确定245.9作为阈值. 表2 阈值的确定Table 2 Decision on threshold 由于阈值是ICA进化的结果,同时又大于¯Q,故阈值大小合适.表3给出了关于各个实例的阈值以及三种算法最终所获得的非劣解所对应的实际能耗,其中ATEC和MTEC表示非劣解集中所有非劣解的最小能耗值和平均能耗值. 如表3所示,三种算法关于所有实例所得到的ATEC和MTEC都小于QEC,而且关于大多数实例这两个指标都与QEC接近,这说明第二阶段总能耗的下降速度显著降低了,从而说明第二阶段的新旧解更替原则和集合的更新策略是合理的,第二阶段主要用于目标函数f1,f2的最小化处理. 表4和5描述了三种算法的计算结果和计算时间,可以看出,两阶段算法关于几乎所有实例所产生的结果明显由于另外两种算法.两阶段算法关于19个实例提供了参考集的所有元素,而NSGA-II和VNS关于这19个实例所获得的解都受两阶段算法的非劣解支配,NSGA-II只是关于Ka10×7产生了参考集的全部成员,MK06的参考集全部都由VNS提供,另外,NSGA-II和VNS搜索所得的解总是距参考集较远,总之,两阶段算法利用和另外两种算法相似的计算时间取得了明显占优的计算结果. 表3 总能耗阈值和三种算法的ATEC和MTECTable 3 Total energy consumption threshold and ATEC and MTEC of three algorithms InstanceQEC两阶段算法 NSGA-II VNS ATEC MTEC ATEC MTEC ATEC MTEC MK10 9728 8537.1 8536.2 8991.6 8955.6 9022.7 8972.6 MK1112890 12415 12276 12640 12577 12417 12353 MK1214933 14291 14220 14314 14148 14214 14109 MK1314202 13131 13104 13845 13763 13382 13310 MK1416985 14916 14856 15307 15239 15020 14981 MK1517000 13793 13656 13877 13786 13643 13612 DP1 34534 33829 33745 34117 34026 33902 33758 DP2 40332 38574 38394 38874 38813 38654 38512 DP3 36428 35271 35086 35701 35504 35367 35215 DP4 36880 36171 35656 36077 35742 36225 36089 DP5 40085 38815 38766 39428 39252 38882 38619 DP6 37091 35882 35729 36445 36162 36185 35897 DP7 26373 60667 60542 61033 60989 60707 60673 DP8 52422 49948 49870 50638 50627 50722 50527 DP9 64539 62395 62232 63458 63202 63282 62966 DP10 60350 58580 58133 59242 59145 59277 59070 DP11 57613 55548 55373 56332 56260 56118 55612 DP12 60711 58022 57981 59288 58947 58260 58220 DP13 86142 84382 84335 85046 85027 85200 85062 DP14 83000 80940 80803 82332 82135 81889 81787 DP15 73000 70977 70631 72033 71854 71800 71702 DP16 80468 78790 78584 79976 79878 79417 79266 DP17 86677 84886 84798 85963 85675 85394 85324 DP18 86330 84114 83685 84951 84785 85045 84679 表4 三种算法的计算结果Table 4 Computational results of three algorithms Instance DIRρl两阶段算法NSGA-II VNS两阶段算法NSGA-II VNS DP3 1.424 37.62 5.638 0.915 0.000 0.085 DP4 1427 2911 7302 0.750 0.000 0.250 DP5 5.861 50.89 4.452 0.583 0.000 0.417 DP6 0.000 52.16 12.64 1.000 0.00 0.00 DP7 0.000 33.53 19.41 1.000 0.00 0.00 DP8 0.652 42.3 20.47 0.988 0.000 0.012 DP9 0.000 66.43 34.33 1.000 0.00 0.00 DP10 0.543 4836 11.20 0.950 0.000 0.050 DP11 0.000 34.21 14.03 1.000 0.00 0.00 DP12 2.597 67.65 4.814 0.667 0.000 0.333 DP13 0.00 3326 20.31 1.000 0.00 0.00 DP14 0.258 46.08 1264 0.981 0.000 0.019 DP15 0.000 46.20 19.04 1.000 0.00 0.00 DP16 0.000 67.34 44.41 1.000 0.00 0.00 DP17 0.000 34.69 16.09 1.000 0.00 0.00 DP18 0.000 39.64 21.59 1.000 0.00 0.00 表5 三种算法的计算时间Table 5 Comparisons on the computational times of three algorithms 两阶段算法的优良性能主要来自于算法的两阶段结构以及全局搜索和局部搜索的良好协调,而ICA和VNS的一些改进策略进一步增强了算法性能,因此,两阶段算法是解决具有总能耗约束的FJSP具有较强竞争力的方法. 尽管FJSP已得到较充分的研究,但具有总能耗约束的多目标FJSP的研究相对较少,随着绿色制造和低碳制造的应用不断深入,需要进一步研究节能FJSP.本文提出一种基于ICA和VNS的两阶段算法在总能耗不超过给定的阈值条件下最小化Makespan和总延迟时间.第一阶段将原问题转化为包括总能耗的三目标FJSP,然后利用新策略构建ICA以优化转化后的FJSP,并根据第一阶段的结果确定总能耗阈值;第二阶段则运用一种高效的VNS对原问题求解.计算结果表明,两阶段算法具有较强的搜索性能和优势. 未来我们将继续深入研究具有总能耗或峰值能耗约束的调度问题,并进一步研究帝国竞争算法在低碳生产调度方面的应用;另外,分布式调度也是我们未来研究的主题之一.2 求解具有总能耗约束的FJSP的双阶段算法
2.1 编码
2.2 第一阶段:ICA

2.3 第二阶段:VNS
2.4 算法描述:两阶段算法
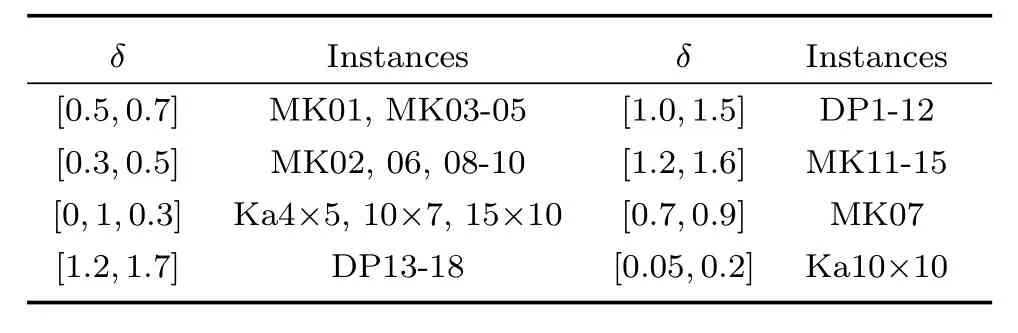
3 计算实验


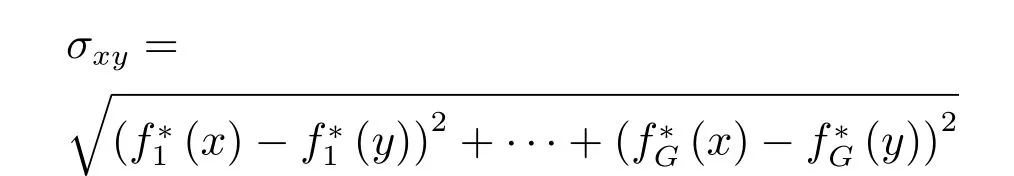



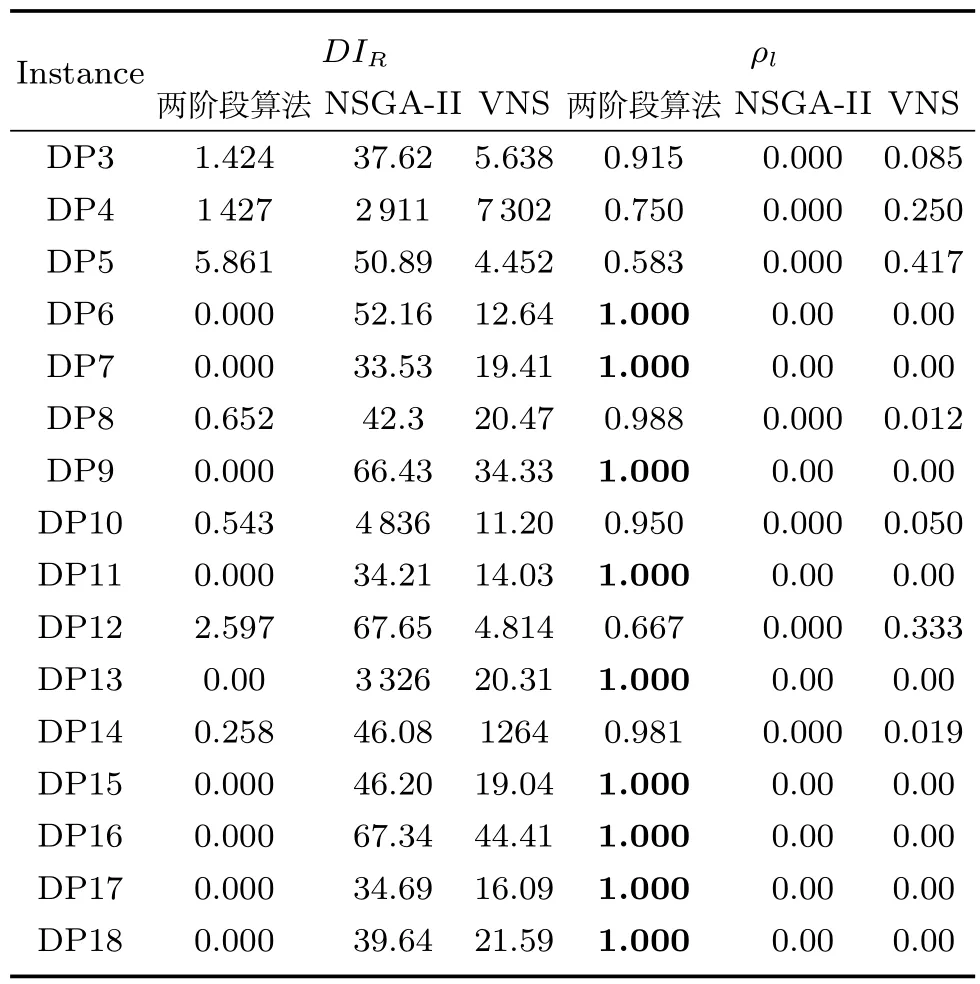
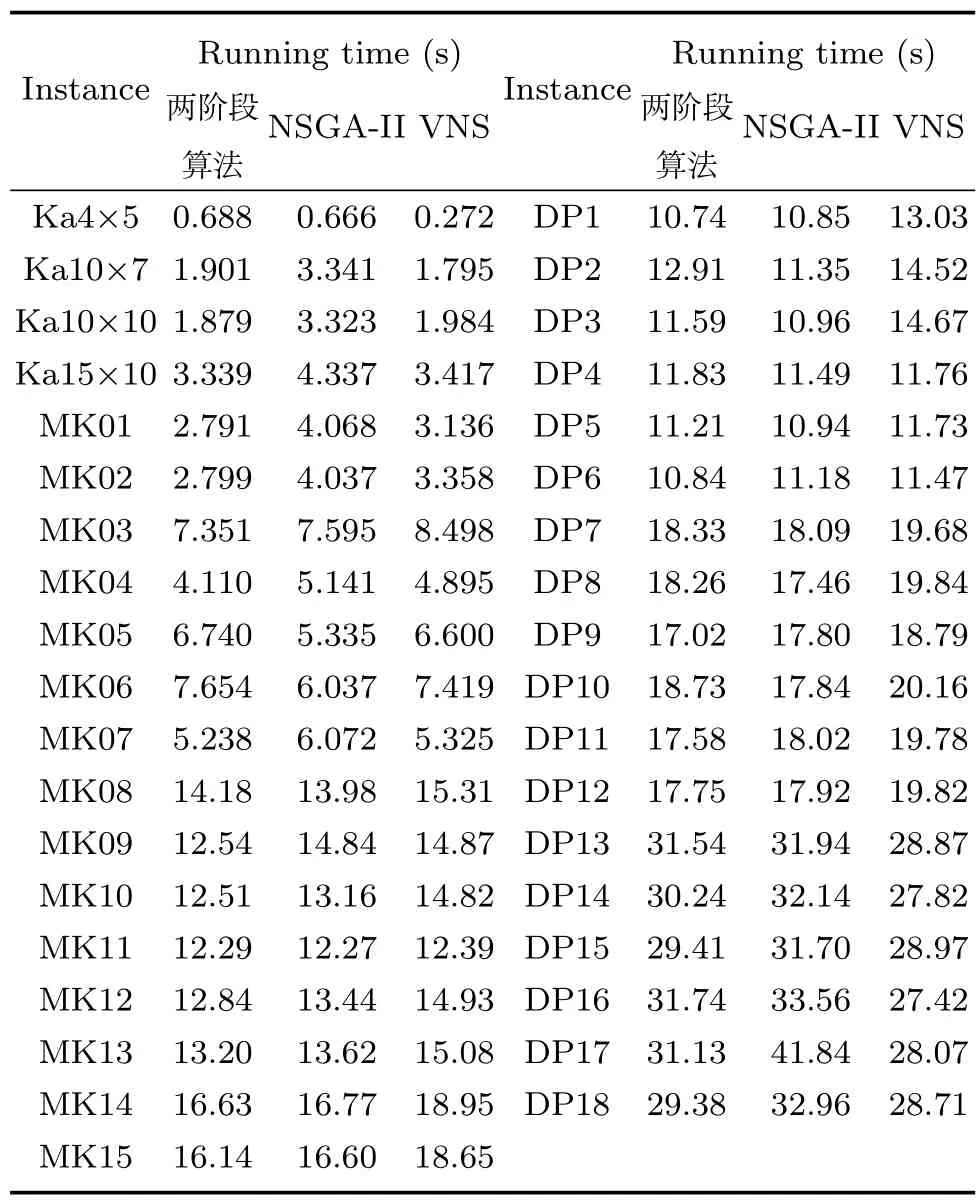
4 结论
