城市社区公共设施数量配置与空间布局模型及其应用

杨西宁，程志刚

(安徽省城乡规划设计研究院，安徽 合肥 230022)

0 引言

社区是城市的基本细胞，是维持城市功能正常发挥的基本空间单元。社区中的公共设施为人们提供如教育、商业娱乐、医疗卫生、文化体育、金融邮电、行政管理、市政公用等各种公共服务，是保证社区正常运转的关键节点与核心要素。社区公共设施的规划布局事关居民的日常生活，是生活是否便利的重要衡量指标。目前，国家在城市社区公共设施规划布局上采用的是基于千人指标法的配套模式[1～3]。这种模式建立在每个社区都是一个封闭的静态系统并且公共设施都是自给自足的假设之上[4]，实际操作中，这种模式带来了一些问题。首先，社区公共设施的完全自我满足尚无法实现。其次，各自为政、自成一体的自我配套使得各个社区都形成一个个独立的小社会，这使得相邻社区之间的公共设施整合与资源共享无法实现，由此导致公共设施的使用效率低下，更重要的是造成了严重的资源浪费。最后，用千人指标法进行公共设施规划布局时，其能较为直观地反映社区所需公共设施的配置数量，由此发挥重要的规划协调作用[5]，但其不能确定各个公共设施的具体空间位置，更不能确定各个公共设施所处的最优空间位置。这使得目前社区公共设施的空间选址具有很大的随意性和主观性，缺乏精确地定量分析和计算，空间选址结果也常常因人而异。而这又可能进一步导致公共设施空间布局不合理，由此带来使用效率低下和一些不合理与不必要的交通成本，从而再次造成资源浪费。

本质上看，社区公共设施规划布局也是一个公共资源的规划布局问题，同时又是一个典型的区位配置问题[6～10]。但是，不同于城市大尺度层面上的公共设施(如消防站、医院、垃圾站、加油站等)规划布局[11～15]。社区是一个尺度更小的城市空间，为其配置的公共设施数量和类型均较多，但与城市级的公共设施相比，社区公共设施的规模较小。同时，在千人指标作为一项国家标准仍在实行的背景下，社区公共设施的规划布局还要满足这个要求。目前，城市公共设施规划布局方法，如中值模型[16]、Voronoi图模型[17]、概率模型[18]、最大覆盖选址模型[19]、复杂网络聚类模型[20]、分级层次选址模型[21～23]、空间分析及遗传算法选址模型[24]、GIS 空间分析模型[25～27]等都没有考虑到千人指标要求，难以在社区小尺度层面上的公共设施规划布局中应用。因此，社区公共设施规划布局必然要在方法上进行改进和优化，从而既能满足国家标准要求，又能有效避免上述弊端，由此做到公共设施的充分利用和资源的最大节约。

基于此，本文在千人指标法的基础上，构建了社区公共设施规划布局的模型和方法，并采用现代交互式搜索算法进行求解，从而既能得到社区公共设施的最佳配置数量，又能得到公共设施的最优空间位置，由此实现科学合理的社区公共设施规划布局。

1 模型和方法

社区公共设施是一种公共资源产品，其规划布局的根本目的在于合理确定资源或服务供给者(公共设施)的数量和位置。在社区规划建设中，要求在合理的空间位置上规划布局公共设施，使之能够在相等投入的基础上尽可能服务更多的居民。简言之，就是以最小的投入来获取最大的收益。同时，还要科学合理地计算社区公共设施的配置数量，使其既能充分满足居民需要又能做到不过度配置而产生资源浪费。这样，如何实现社区公共设施在空间上的最优布局和确定其最佳数量是社区公共设施规划的两大技术焦点。

加大产品质量管理力度，实行质量监督制度，及时制修订有关工程技术规范并制定完善行业标准，加大监督力度，对产品实行推广认定、监督检查和进场复查，禁止假冒伪劣产品用于建设市场，同时规范市场行为，防止以次充好、低价销售等不良竞争行为发生，促进行业市场健康有序发展。

每个社区和每项公共设施都是具有一定面积的面状区域，为便于分析，通常以点的形式来表达，其中，社区是需求点，公共设施是供应点。本文将社区和公共设施抽象为空间坐标点，以面状区域几何中心的平面坐标(x，y)代表社区和公共设施的空间位置。设有m个城市社区，每个社区的居住人口为 pi(i=1，2，3，…，m)，利用现行的社区公共设施配套的千人指标法，计算得到m个社区公共设施的配置数量n，公式如下：

根据(1)式的计算结果，可把社区公共设施规划布局分为n＜m和n≥m两种情况，总体技术路线可总结为如图1所示。

1.1 n＜m情况

公共设施配置数量。若n为整数，此即为m个社区公共设施的配置数量；若n为小数，本着资源节约和方便居民的原则，采用四舍五入法计算m个社区公共设施的配置数量。特别的，当四舍五入后的n等于m时，则按n≥m时的情况进行公共设施的规划布局。

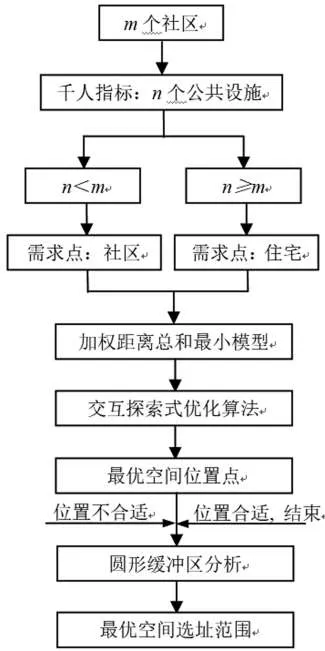
图1 社区公共设施规划布局技术路线

公共设施空间选址。当n＜m时，每个社区分配的公共设施平均数量将小于1。此时若再按照千人指标法为每个社区配套公共设施必然会产生过度配套而造成资源浪费。因此，在m个社区所需公共设施总量一定(即n)的情况下，必然存在多个社区共用1个公共设施的情况。这样，社区公共设施规划布局要做的就是把这n个公共设施布置到最优的空间位置上，具体方法为：

建立科学的教师专业标准是教师从一种“职业”成为一种“专业”的基本标志，是客观评价教育质量的依据[10]。然而，体育教育在整个教育领域中处于边缘地位，与其他学科的教师相比，体育教师似乎也低人一等。体育教师的专业发展的生涯始于进入大学的体育教育专业，但是，无论是职前的培养、毕业，还是新体育教师的准入、职后的培训，都处于“无章可循”的状态[11] 。因此，制定体育教师的专业标准迫在眉睫。在个体层面，职前、职后的专业标准为体育教师提供衡量自身专业水平的基本准则；在群体层面，专业标准形成体育教师之间专业对话的交流工具；在组织层面，为机构在选择、培训体育教师方面提供准则。

设i是m个社区中的任意一个，(xi，yi)是已知社区的空间位置坐标点(i=1，2，3，…，m)；j是 n 个公共设施中的任意一个，(xj，yj)是要计算的社区公共设施的空间位置坐标点(j=1，2，3，…，n)。寻找n个公共设施的最优空间位置意味着使得每个社区i都被分配到与其距离最近的公共设施j的服务范围内，同时要求m个社区和n个公共设施之间的加权距离总和达到最小值，这将使得整体距离耗费最小，在速度一定的情况下，所需到达时间也最少，此时的公共设施空间位置就是所求的最优空间位置。由此，建立选址模型为：

其中，dij是社区i与公共设施j之间的最短距离，表示每个社区i都被分配到与其空间距离最近的公共设施j的服务范围内，dij的计算公式为：

wi是社区i被赋予的权重。由于社区人口数量pi是决定公共设施规划布局的最重要因素，因此wi定义为社区人口pi占m个社区总人口的比率，即wi为：

2.2 基于K-means算法的优秀班集体评选方法首先将真实数据集按年级进行划分，分别得到2015级、2016级和2017级各班级的参评数据，然后从3个年级的数据集当中分别选取所有属性取值较平均的班级（均衡发展班级）、若干属性取值较大的班级（偏离发展班级）和大多数属性取值较小的班级（最差发展班级）作为初始聚类的中心，按K-means聚类算法的执行过程，将各年级的数据集分别聚为3类，最后将均衡发展的类内的班级作为本年级的优秀班集体。具体的实现过程如下。

式(5)能保证每个社区只能接受一个公共设施的服务，但并不排斥每个公共设施可向多个社区提供服务，从而保证了公共资源能够得到节约集约利用。

aij表示了社区i与公共设施j之间的关系。当社区i与公共设施j距离最近即i当且仅当由j提供公共服务时，aij为1，否则为0。为了避免两个或两个以上的公共设施向同一个社区重复提供公共服务，此处增加一个限制条件，即：

式(2)是一个典型的空间寻优问题，在此采用交互探索式优化算法进行求解，从而得到n个公共设施的最优空间位置，主要步骤如下：

(a)首先随机产生n个公共设施的初始位置点(xj，yj)。

那段时间，日子是灰色的。钱海燕觉得自己的整个世界都坍塌了。婚后这一年，周启明将她宠得像个孩子，现在他倒下了，她只能扛起所有的事。

当ni≤1时，以方便社区居民为原则，取第i个社区公共设施的数量为1。当ni＞1时，若ni为整数，则即为第i个社区公共设施的配置数量；若ni为小数，本着资源节约和方便居民的原则，采用四舍五入法计算第i个社区公共设施的配置数量。

(c)公共设施点j的最优空间位置就是使(2)式取得最小值时的空间位置。由(2)式可知，若总体加权距离和取得最小，就必须使每组社区中的社区和为其提供服务的一个公共设施点之间的加权距离总和取得最小，此时该组社区的公共设施点和其他组中的社区之间的加权距离和为0(因为aij=0)。这样，n个公共设施点的最优空间布局问题就转化为n组社区中的单一公共设施点的最优空间布局问题，即由多点寻优转化为单点寻优。

(d)对于每组社区集合(设其中有l个社区)，计算该组社区的单个公共设施点j的最优空间位置，也即j到该组所有社区点i的总加权距离和最小时的位置。此时，由于aij=1，同时又只有一个公共设施点，所以式(2)可以简化为：

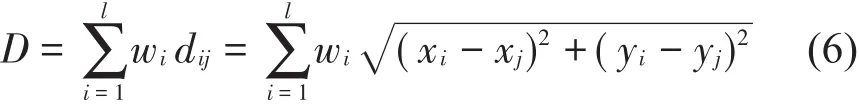
对于上式的二元函数来说，若使D最小，也就是要求此函数的各个变量的偏导数等于0，由此计算得到 xj和 yj。

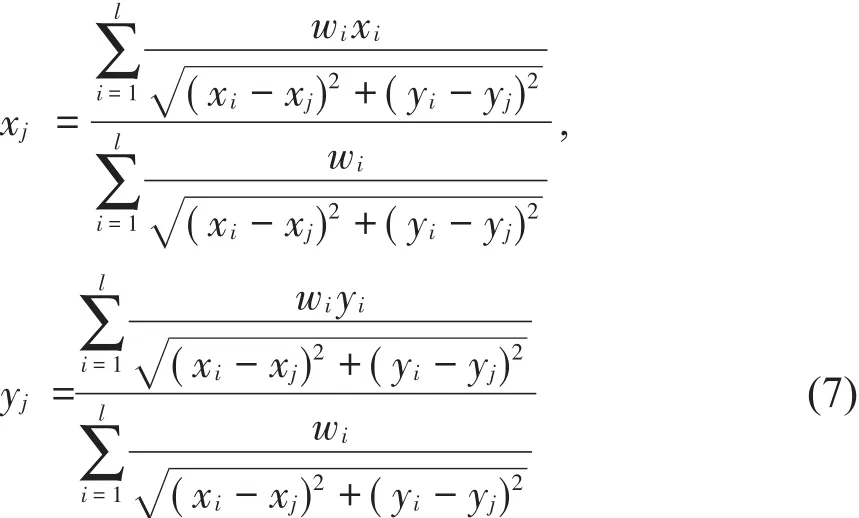
(e)式(7)中，方程两侧都有 xj和 yj，因此并没有求出公共设施点的最优空间位置。为此，采用迭代算法进行求解。将该组社区空间范围中的任意一个位置(x1，y1)赋给式(7)的右侧，由此解出左边的xj和yj。如此多次迭代计算，当左边求出的xj和yj与右侧给出的位置值足够接近时，即二者之间的差距均小于一个预设的容许差值时(如0.1)，则可以停止计算，此时求得的(xj，yj)就是该组社区集合中单个公共设施点的最优空间位置。

贯通培养项目致力于培养具备扎实的基础知识和一定的实践能力与创新能力的高端技术技能人才。相比于普通高中的学生，贯通培养项目高中阶段的学生摆脱了应试教育的藩篱，教师可以更多地关注如何培养学生的语言交际能力，因此他们的学习内容要更加突出实用性和实践性。同时，贯通培养项目的学生经过两年的高中阶段学习后将升入大专，比普通高中的学生更早面临专业和职业的选择。因此，贯通培养项目高中阶段的英语视听说选修课的教材编写和课程设计必须兼顾专业性和职业性。

(f)对n组社区集合分别按照步骤(e)进行计算，由此得到n个公共设施的最优空间位置点，此时，式(2)和式(6)都将取得最小值。

(g)为了保证上述所得结果是全局最优，可以在步骤(a)的初始阶段定义至少3套不同的起始点方案进行验证。如果循环运行到最后，所得结果是一致的，就可以认为结果具有全局最优性。否则，结果只具有局部最优性，需要重复上述步骤(a)～(f)，直至得到全局最优解。

1.2 n≥m情况

公共设施配置数量。此时，每个社区分配的公共设施平均数量将大于或等于1，第i个社区公共设施的数量 ni(i=1，2，3，…，m)按千人指标法进行计算，公式为：

(b)将m个社区空间位置点分成若干组，使得每组中的社区点i都被分配给与其距离最近的公共设施点j，此即由j为i提供服务，由此获得对应n个公共设施点的n组社区的集合。这样，每组社区集合都将分配到一个公共设施点，该公共设施点是所有的n个公共设施点中距离该组社区集合中的各个社区空间距离最近的点，该公共设施点当且仅当为该组社区中的各个社区提供服务(aij=1)，而不为其它组中的社区提供公共(aij=0)。

至此，以千人指标法为基础，构建了社区公共设施数量配置和空间选址的规划布局模型和方法。其以社区本身(n＜m)或社区住宅(n≥m)为需求点，通过千人指标法计算配置数量，利用加权距离总和最小模型和圆形缓冲区分析法获得最优空间位置点和最优空间选址范围，由此既能使得不同社区能够共享公共设施而实现资源节约，又能获得最优空间位置而方便居民使用。

每栋住宅建筑都是具有一定面积的面状区域，仍可将其抽象为空间坐标点，以面状区域几何中心的平面坐标(x，y)代表每栋住宅建筑的空间位置。设第i个社区拥有s栋住宅(即s个需求点)，每栋住宅的居住人口为 tk(k=1，2，3，…，s)。tk可经实际调查得到，当条件不允许时，也可由每栋住宅的总户数乘以社区所在城市的户均人口数估算得到。

那么比如说，有的时候看了一些具有社会学、民俗学价值的小说以后是有些体会的。最近因为搞鸳鸯蝴蝶派，我就看了张恨水的《春明外史》，这本书100万字，看完之后我当然对张恨水也有一个具体的了解，而且得到很大的收获。如果现在让我讲鲁迅《社戏》的前半篇，那么这个一百万字就给我起了一种民俗学的参考作用，因为它讲北京的戏院讲得太详细了，写各种各样背景的剧院，而这种剧场以前在我的脑子里是非常空泛的。你如果去读茅盾的《幻灭》《动摇》《追求》，你读《动摇》的时候对大革命这一段时期的生活就会比较具体化，不读的话就是很抽象的在讲大革命。

特别的，当m=1即只有1个社区时，按照方便居民原则，至少要配置1个公共设施，此即n≥m情况，要按照上述n≥m时的方法进行空间选址。

(2)把4个社区分别分配给与其距离最近的卫生站，由此形成2个子区域，每个子区域都有1个卫生站为其中的社区提供服务，如图2(右上)所示。此时即把2个卫生站的多点空间寻优问题转化为2个子区域中的单点寻优问题，目的是使每个子区域的社区和卫生站的加权距离和最小，进而使整体4个社区和2个卫生站之间的加权距离总和最小，从而找到2个卫生站的最优空间位置点。

要指出的是，应用上述模型和方法得到的公共设施空间位置将是一个精确的坐标点，但在实际操作中，该点可能是一个并不适合的位置，例如可能是道路、水体或已被开发建设。此时，要采用圆形缓冲区法而得到选址的一个空间范围，缓冲区的中心为计算得到的空间位置点，半径可根据实际情况灵活决定，在缓冲区圆形空间范围内的任意一个适宜位置布置公共设施都是实现了最优布局。

公共设施空间选址。每个社区都是由不同的建筑物所组成，总体上，这些建筑物可分为住宅建设和非住宅建筑两大类。其中，非住宅建筑是为居民提供各种服务的公共建筑。因此，当某个社区公共设施数量一定的情况下，每栋住宅建筑及其居住人口成为社区公共设施的各个需求点，进而成为社区公共设施空间选址的决定因素。

1.2 架藏法：鲜藏的大葱为保证鲜藏的质量，在贮藏前需将大捆大葱打开，剔去受伤，受潮，受冻和腐烂的茎株，分扎成小捆，每捆重约7～10千克，依次堆放在贮藏架上，中间留一捆葱位置的通风空隙，可以横放，也可以竖着放。对贮藏的大葱要加强检查，检查时，可打开葱捆查看，中间如有发热变质的，就及时剔除，防止腐烂蔓延。如发现潮湿现象必须在日光下摊晒晾干后再入库。

2 应用示例

2.1 社区卫生站配置与选址

设有4个社区A、B、C和D，人口分别为300人、400人、600和900人，现在为其配置社区卫生站，要求每千人需要配置1个卫生站。

当第i个社区所需公共设施数量为1时，此即是为s个需求点提供服务的单点寻优问题。当第i个社区所需公共设施数量大于1时，此即是为s个需求点提供服务的多点寻优问题。这两种情况可根据公式(2)的选址模型并再次利用步骤(a)～(g)的交互探索式优化算法进行最优空间位置求解。区别在于把模型中的社区变为住宅，同时，模型中的w要改为每栋住宅被赋予的权重，w定义为每栋住宅的居住人口占s栋住宅居住总人口的比率，即：

卫生站数量。根据公式(1)计算得到4个社区共需要的卫生站数量为2.2，按四舍五入法取为2，此为情况1中的n＜m状态。按照资源节约要求，必然要使多个社区共用1个卫生站。这就要利用最小加权距离和的规划选址模型即公式(2)计算2个卫生站的最优空间位置点。

卫生站选址。根据步骤(a)～(g)进行求解。

(1)在4个社区所形成的空间范围内，随机选择2个卫生站的空间位置点，见图2所示。

Google提出了一套影像分割规范，并对应地开发了一套对应的API［1］，在地理信息行业得到了广泛应用。

图2 卫生站空间选址

第一级别是餐馆：菜马上就来；第二级别是同事：改天请你吃饭；第三级别是领导：我只说两句；第四级别是老公：在开会呢；第五级别是三陪：昨天才来，今刚上班；第六级别是组织部：不让老实人吃亏；第七级别是开发商：房价还会涨；第八级别是医院：我们已经尽力了；第九级别是教育部：再穷不能穷教育！

(3)对每个子区域的单个卫生站的最优空间位置按照公式(7)进行迭代计算，得到卫生站的新位置如图2(右下)所示。当两次迭代计算的结果差距小于预设的容许差值时(0.1)，便得到每个子区域中单个卫生站的最优空间位置如图2所示，由此获得2个卫生站的最优空间位置点。

为了保证上述所得结果是全局最优，可以定义至少3套不同的2个卫生站的起始点方案进行验证，如果最后所得结果是一致的，就可以认为结果具有全局最优性。否则，结果只具有局部最优性，需要重复上述计算步骤。

最后，如果选址点不合适，则以计算得到的2个卫生站的坐标点为圆心，以500 m(此即人步行可达的服务半径上限)为半径进行圆形缓冲区分析，得到2个卫生站选址的空间布局范围，卫生站只要规划布置在此圆形缓冲区内就实现了最优空间布局。

2.2 社区活动室配置与选址

设有4个社区A、B、C和D，人口分别为1600人、700人、1300和2000人，现在为其配套社区卫生站，要求每千人需要配套1个活动室。

活动室数量。根据公式(1)计算得到4个社区共需要的活动室数量为5.6。显然，此即为n≥m的情况。首先由公式(8)计算得到每个社区配置活动室数量的初始值，进而根据配置原则得到最终的配置数量，结果见表1。

《饥饿艺术家》是卡夫卡写于1922年春的短篇小说，发表于同年10月《新观察》，为作者自己所珍重的几个短篇小说之一。1924年作者曾以此为书名，与其他三个短篇结集出版。同年4月，即在他去世前一个多月，他在病榻上阅读本篇清样时，不禁泪流满面，可见与书中主人公发生共鸣。该集子出版时，作者已辞世。

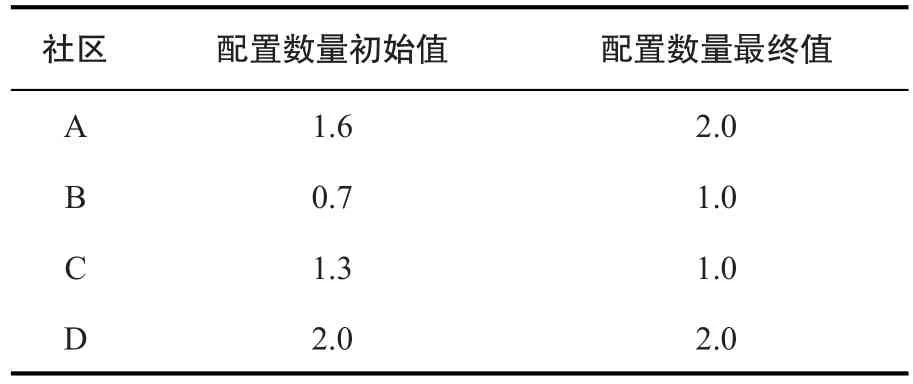
表1 活动室配置数量

活动室选址。社区B和C都需配置1个活动室，此即是为社区B和C的住宅及其居住人口提供服务的单点寻优问题。社区A和D都需配置2个活动室，此即是为社区A和D的住宅及其居住人口提供服务的多点寻优问题。

以社区A为例，设其有32栋住宅建筑(图3)，即32个需求点，现在即计算为这32个需求点服务的2个活动室的最优空间位置。利用(9)式计算住宅建筑的权重，进而根据步骤(a)～(g)的交互探索式优化算法进行求解，得到2个活动室的最优空间位置点(图4中黑点所示)。同理，依次求解社区B、C、D所需配置活动室的最优空间位置。

法律认同是现代国家走向法律趋同的最佳方式，也是改变发展中国家一味依赖发达国家法律规则的现状，增强自身法律制度世界影响力和竞争力的契机。就我国而言，虽然经济总量位居世界前列，但非传统经济大国，法律的世界影响力比较有限，所以，以法律认同的方式提升我国法律的国际地位，具有更为重要的积极意义。

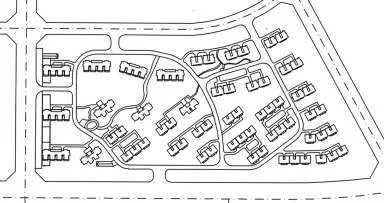
图3 社区A住宅布局平面图

图4 社区A活动室空间选址结果

最后，如果计算得到的选址位置点不合适，同样以计算得到的活动室的坐标点为圆心，以500 m为半径进行圆形缓冲区分析，得到活动室选址的空间布局范围，活动室只要规划布置在此圆形缓冲区内就实现了最优空间布局。

图5 选址缓冲区示意图

上述算例表明，这种模型和方法既结合了千人指标法，又对其进行了改进和优化，从而得到社区公共设施最合适的配置数量和最优的空间位置，由此为社区公共设施规划布局提供了科学理性的决策依据。

表4和表5为PB实验设计及结果分析。由表5可以看出，PB实验的模型P值为0.0004（小于0.01），达到极显著，该模型具有统计学意义。从各因素的P值可知，各因素对酸奶品质的影响力从高到低为果汁添加量＞白糖添加量＞发酵温度＞奶粉添加量＞菌粉添加量，其中果汁添加量、白糖添加量、发酵温度达极显著水平（P＜0.01）。从系数估值可知，白糖添加量和发酵温度对酸奶品质呈正效应影响，其余因素为负效应影响。选择Box-Behnken试验时至少需要3个因素，因此，结合各因素的P值大小，选择果汁添加量、白糖添加量和发酵温度这3个因素进行最陡爬坡实验。

3 结论与讨论

本文突破了社区是封闭系统的传统思路，在千人指标法的基础上，以公共资源共享的开放社区系统为理念，初步构建了社区公共设施规划布局的优化模型，为该类问题的解决提供了一种新思路和新方法。基于这种模型与方法的实例测试表明，应用本文提出的模型和方法可以提高社区公共设施规划布局的精准度和科学性，能有效克服传统方法的不足，同时可为同类型问题的解决提供一定的理论参考和方法借鉴。

最后应指出，本文是社区公共设施规划布局方法研究上的一种尝试，从理论模型上给出了社区公共设施数量配置和空间布局的技术方法，但研究还存在一些有待探讨的地方：首先，本文提出的规划模型仍是理论上的探索，是一种理想化的分析研究，而实际应用上则要受到更多的影响因素，例如要考虑社区的区位因素、人口结构、服务半径等对公共服务设施数量配置和空间布局的影响和约束；在算法上，是否可以采用更先进的智能优化算法，从而获得更优的空间布局结果；此外，这种模型和方法仍需大量的实践验证。尽管存在着种种不足，但也应看到社区公共设施配置是一个复杂系统的科学决策过程，是一种对客观事物不断深化的认识过程，不可能一蹴而就。本文研究正是一次大胆尝试，是社区公共设施规划技术方法层面上的一种有益探索。相信随着未来研究的不断深入，社区公共设施规划布局的技术方法体系将更加完善和成熟，由此可为实践应用提供更科学的决策支持。