带胸墙斜坡堤单波越浪量的数值研究

王 键，孙大鹏，吴 浩

(大连理工大学 海岸与近海工程国家重点实验室， 大连 116024)

越浪是斜坡堤设计时关注的重要指标，目前反映越浪效果的参数主要有平均越浪量和单波越浪量两种，其中平均越浪量适用于反映越浪的长期效果；而对于越浪的瞬时效果(例如：波列中个别大浪对斜坡堤结构的稳定性及堤后行人和车辆安全的影响等)，就需要采用单波越浪量(单位堤长上单个波浪产生的越浪水体体积)来作为评估指标。由于波浪的随机性，单波越浪量的大小也是随机的，工程设计中通常采用某一超值累积频率(例如：1%)的单波越浪量作为允许越浪量的控制指标。目前关于越浪量的研究多针对于平均越浪量[1-3]。而对于单波越浪量问题的研究则相对较少，Franco C和Franco L[4]通过物理模型试验对非破碎波浪在直立堤上的单波越浪量分布和单波越浪量进行研究，应用两参数Weibull分布函数对单波越浪量超值累计频率进行拟合，进而通过数学推导给出了直立堤上单波越浪量的计算公式；Besley[5]和Van der Meer[6]均采用两参数Weibull分布函数拟合超值累计频率，给出了斜坡堤的单波越浪量的概率分布函数和单波越浪量的计算公式；Victor和Van der Meer[7]针对较低堤顶超高的光滑不透水无胸墙斜坡堤的单波越浪分布进行了系统的试验研究，给出了Weibull分布参数的计算公式；李晓亮等[8]通过三维物模试验，给出了斜向和多向不规则波作用无胸墙斜坡堤单波越浪量的计算公式；范红霞[9]通过物模试验对斜坡堤最大越浪量分布及影响因素进行了研究。

目前关于斜坡堤单波越浪量的研究多针对于无胸墙斜坡堤，且成果大多基于物模试验；而由于人力物力等因素限制，物模试验成果相对有限，尤其是带胸墙斜坡堤单波越浪量的相关研究成果。本文借助FLUENT软件，建立无二次反射的不规则波数值水槽，对斜坡堤越浪进行数值模拟。在和已有物模试验成果对比验证的基础上，分析给出了带胸墙斜坡堤单波越浪量的计算关系式。

1 控制方程

本文采用二维粘性流体的连续性方程，动量方程作为基本 控制方程，VOF法捕捉水体自由表面。相应方程如下：

(1)

(2)

(3)

(4)

式中：ρ为流体密度；u和w分别为x和z方向的速度；p为压强；μ为粘性系数；Fx和Fy分别为附加的源项；F为流体体积函数。

2 数值水槽

2.1 主动吸收式造波

不规则波与结构物作用，模拟时间较长，波浪会在建筑物与造波板之间产生多次反射，这将改变水槽内的波浪特性，影响模拟准确度。为了消除造波端的二次反射波，本文采用Frigaard和Christensen[10]提出的主动吸收式造波理论建立数值水槽。其原理如下：在水槽造波边界前端放置两个浪高仪实时采集波面变化，将采集的波面信号通过滤波变换求出造波修正信号，根据修正信号在造波端添加额外造波速度吸收掉反射波，最终消除造波端的二次反射。

根据上述方法，采用等分能量法划分不规则波频率区间，得到造波板速度为

(5)

M为频率区间划分段数，本文取M=100；ηp和ηm分别为造波端目标波面和实际波面；Kni，Kfi表示水动力传递系数；X0为原始造波信号；X*p为造波修正信号，表达为

(6)

式中：X*p表示p·Δt时刻的造波修正信号；ηp-j表示采集的(p-j)·Δt时刻实时波面数据；N表示滤波器数组长度；hj表示t=j·Δt时刻的滤波系数；Δt表示采集时间间隔。

2.2 数值水槽性能验证

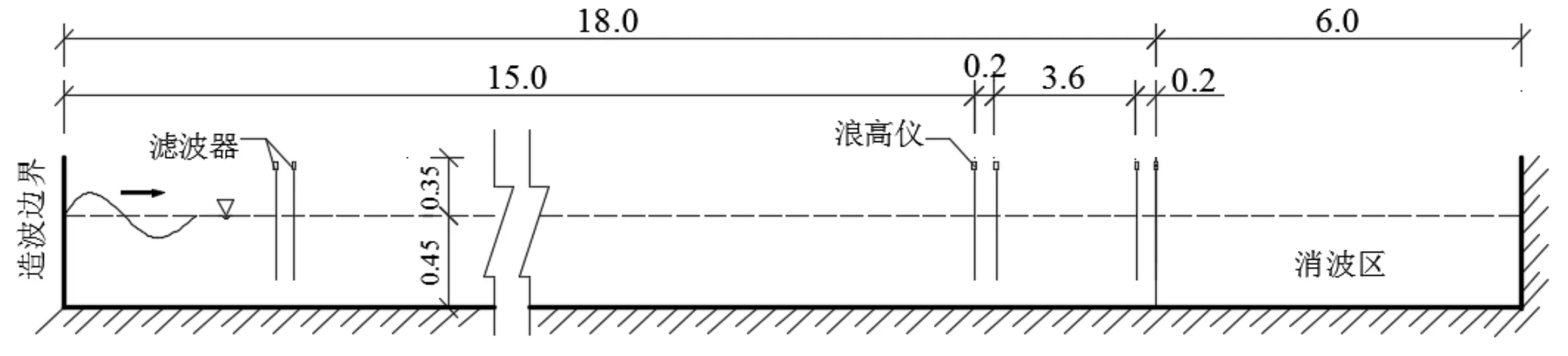
图1 数值水槽示意图(m)Fig.1 Sketch of numerical wave flume

基于上述理论建立数值水槽，水槽的示意图见图1。水槽全长24.0 m，高0.8 m，水槽左边界为造波边界，右侧为6 m长的消波区。

2.2.1 不规则波模拟的有效性验证

采用JONSWAP谱(γ=3.3)作为靶谱，模拟波况：水深d=0.45 m，有效波高Hs=0.094 m，谱峰周期Tp=1.46 s。采集x=15.0 m和18.0 m处的波面数据。根据波面数据，计算得到模拟波谱和统计波要素。图2为模拟谱与靶谱的对比，表1为波要素的模拟值与目标值的对比。可以看到模拟谱与靶谱吻合良好，波要素模拟值和目标值相对误差<5%。结果表明：本文水槽可准确有效地模拟不规则波。

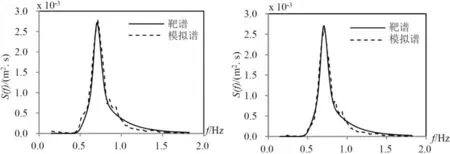
2-a x=15.0 m 2-b x=18.0 m图2 数值水槽不同位置处的模拟谱与靶谱的对比Fig.2 Comparison between simulated spectrum and the target at different locations of the numerical flume

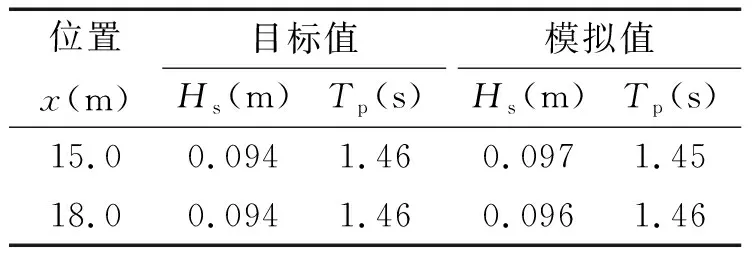
位置x(m)目标值Hs(m)Tp(s)模拟值Hs(m)Tp(s)15.00.0941.460.0971.4518.00.0941.460.0961.46

2.2.2 主动吸收式造波验证

3-a x=15.0 m 3-b x=18.0 m图3 分离的入射谱与靶谱的对比Fig.3 Comparison of the separated incident spectrum and the target

在上一节水槽的基础上，去掉消波区，18.0 m处设置为固壁边界。采集15.0 m、15.2 m、17.8 m和18.0 m处的波面数据，对采集的波面数据进行频谱分析并通过两点法分离出x=15.0 m和18.0 m处的入射谱。图3为分离的入射谱与靶谱的对比图，可以看到入射谱与靶谱吻合较好，表明了本文数值水槽消除二次反射效果良好。

综上所述，本文的数值水槽，可以准确地模拟不规则波，并且能够很好地消除造波端的二次反射；可以运用该水槽进行不规则波与结构物相互作用的数值模拟。

3 斜坡堤越浪量数值模式的验证

3.1 无胸墙斜坡堤的平均越浪量、单波越浪量

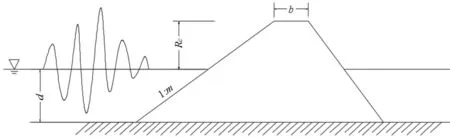
图4 无胸墙斜坡堤示意图Fig.4 Sketch of sloping breakwater without crown-wall

李晓亮等[8，11]对斜向和多向不规则波作用无胸墙斜坡堤越浪进行了系统的物模试验(试验断面如图4)，给出了不规则波作用下无胸墙斜坡堤平均越浪量和最大单波越浪量的计算公式。本文对李晓亮等[8，11]试验中单向波正向入射的部分工况(护面结构为混凝土板)进行数值模拟，采用堤脚处波浪时间序列及越浪历时曲线计算每个波浪所对应单波越浪量，给出平均越浪量和最大单波越浪量Vmax(波列中单波越浪量的最大值)，并与李晓亮等[8，11]的物模试验结果进行了对比。图5给出了两种模拟工况的越浪历时曲线，图6给出了堤脚处单波波高H与相应的单波越浪量V的对比图，表2给出了本文数模值与李晓亮等[8，11]的物模值的对比。

图5 无胸墙斜坡堤越浪量历时曲线Fig.5 Duration curve of overtopping flux of sloping breakwater without crown-wall

图6 无胸墙斜坡堤堤脚波高与相应的单波越浪量的对比Fig.6 Comparisons between the wave height at the toe of the seawall and corresponding individual wave volume

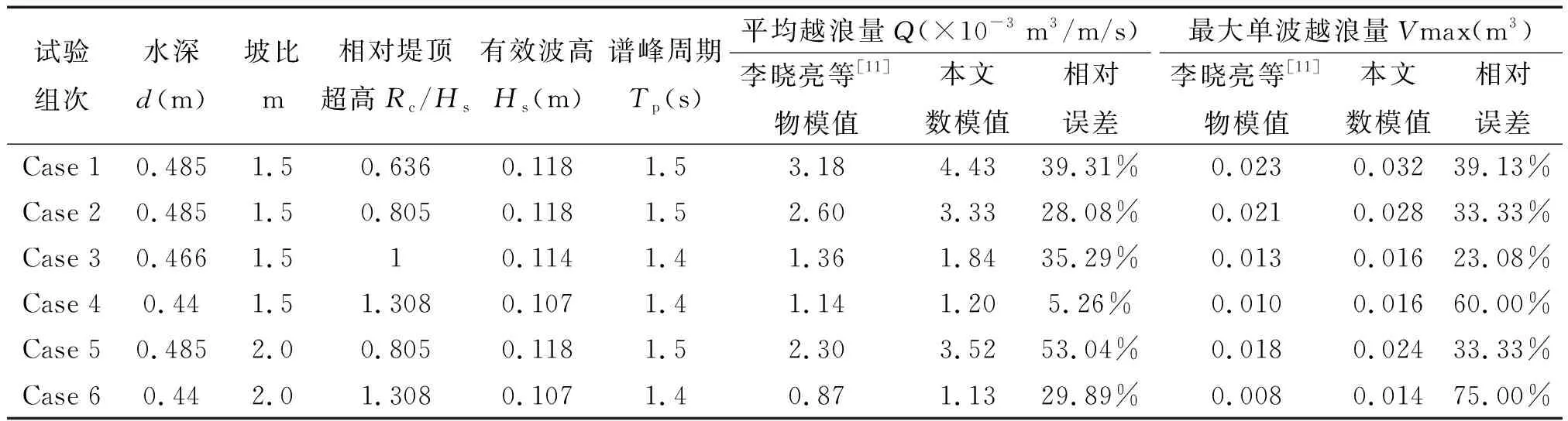
试验组次水深d(m)坡比m相对堤顶超高Rc/Hs有效波高Hs(m)谱峰周期Tp(s)平均越浪量Q(×10-3 m3/m/s)李晓亮等[11]物模值本文数模值相对误差最大单波越浪量Vmax(m3)李晓亮等[11]物模值本文数模值相对误差Case 10.4851.50.6360.1181.53.184.4339.31%0.0230.03239.13%Case 20.4851.50.8050.1181.52.603.3328.08%0.0210.02833.33%Case 30.4661.510.1141.41.361.8435.29%0.0130.01623.08%Case 40.441.51.3080.1071.41.141.205.26%0.0100.01660.00%Case 50.4852.00.8050.1181.52.303.5253.04%0.0180.02433.33%Case 60.442.01.3080.1071.40.871.1329.89%0.0080.01475.00%

从图5和图6可以看出不规则波越浪过程中，较小的波浪不发生越浪，越浪波数量随堤顶超高Rc的增高而减少，堤脚处所测单波波高H与相应的单波越浪量V具有较明显的相关关系，这与实际物理现象是相吻合的。根据表2的结果，可以看出本文数模的平均越浪量和最大单波越浪量的模拟值均比李晓亮[8，11]物模试验结果偏大，造成偏差的可能原因：在数值模式中忽略了波浪爬高破碎过程中的能量耗散；同时发现表中越浪量较小时(case4和case6)的最大单波越浪量的相对误差比平均越浪量的相对误差要大，原因可能是：当越浪量较小时，往往伴随着波浪的破碎飞溅等现象，这些现象增大了单波越浪量的随机性。但本文数模值与李晓亮[8，11]物模值总体趋势一致结果较为接近。表明本文数值模式计算的无胸墙斜坡堤平均越浪量及单波越浪量具有较高的精度。

3.2 带胸墙斜坡堤的平均越浪量

图7 带胸墙斜坡堤示意图Fig.7 Sketch of sloping breakwater with crown-wall

当堤顶高程相同时，带胸墙斜坡堤越浪量明显小于无胸墙斜坡堤(波浪与胸墙作用会产生复杂的变形和破碎，损失能量)；因此斜坡堤工程设计更多地采用堤顶设置胸墙的结构型式(图7)。章家昌等[1]通过物模试验对不规则波作用带胸墙斜坡堤的平均越浪量进行了研究。本文对章家昌等[1]的中带胸墙斜坡堤的物模组次(护面结构为混凝土板)进行数值模拟，并将本文数模值与章家昌等[1]的物模值及《港口与航道水文规范》[12]公式计算值进行对比，结果见表3。

从表3对比结果可以看出本文数模值与章家昌等[1]物模值及规范公式计算值吻合良好，同时比规范公式更接近物模试验值。表明了本文数值模式计算的带胸墙斜坡堤平均越浪量具有较高的精度。

鉴于现行规范中还没有带胸墙斜坡堤单波越浪量的计算方法，而一些学者[5，6，8]提出的单波越浪量计算方法也是针对于无胸墙斜坡堤的；因此本文在上述无胸墙斜坡堤平均越浪量、单波越浪量及带胸墙斜坡堤平均越浪量数模值与物模试验值比较、验证的基础上，试图通过数值模拟手段对带胸墙斜坡堤的单波越浪量进行分析探讨。

表3 本文数模值、章家昌等[1]物模值及规范值的对比Tab.3 Comparisons between results of this paper, Zhang Jia Chang[1] and normal value

4 带胸墙斜坡堤单波越浪量的数值研究

4.1 带胸墙斜坡堤单波越浪量的分析方法

由于波浪的随机性，单波越浪量的大小也是随机的，工程设计中通常采用某一超值累积频率(例如：1%)的单波越浪量作为控制指标。对于无胸墙斜坡堤，李晓亮等[8]和Victor和Van der Meer[7]的物模试验结果证实单波越浪量的超值累积频率符合Weibull分布。若超值累积频率符合Weibull分布，则可以给出单波越浪量的计算公式[8]

(7)

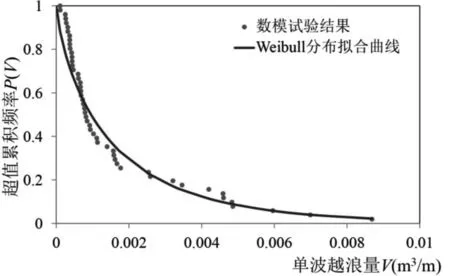
图8 Weibull分布拟合带胸墙斜坡堤单波越浪量的超值概率Fig.8 Fitting of exceedance probability of individual overtopping volume by Weibull distribution function

本文选定超值累积频率1%对应的单波越浪量(下文简称“1%单波越浪量”)为研究对象，参照式(7)设定带胸墙斜坡堤1%单波越浪量的计算关系式

(8)

4.2 经验系数A的影响因素

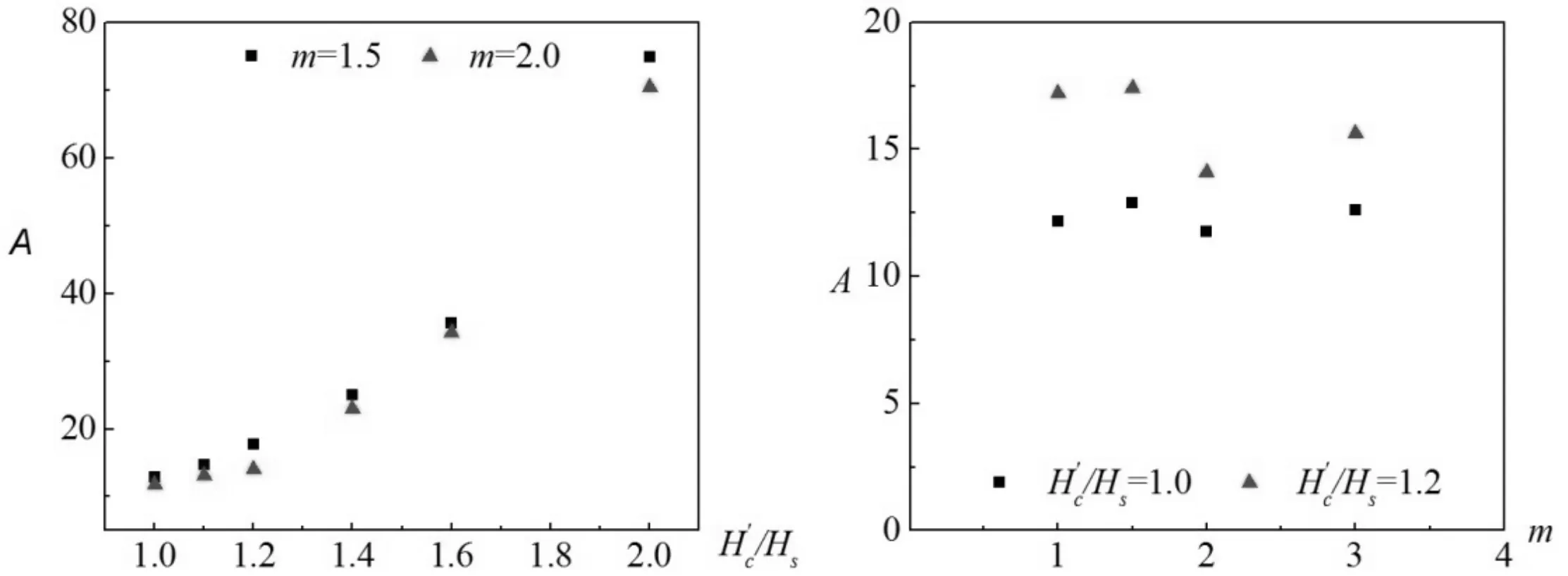
图9 A与的关系图10 A与m的关系Fig.9 Relational graph of /Hs Fig.10 Relational graph of versus A m versus A

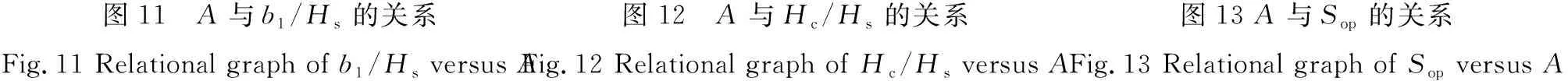
图11 A与b1 /Hs的关系Fig.11 Relational graph of b1/Hs versus A图12 A与Hc /Hs的关系Fig.12 Relational graph of Hc/Hs versus A图13 A与Sop的关系Fig.13 Relational graph of Sop versus A

4.3 带胸墙斜坡堤单波越浪量的计算

4.3.1 计算关系式

(9)

表4 式(9)中的系数取值Tab.4 The value of the coefficient in formula 9th

经非线性拟合，式(9)中的待定系数a、b、c、d取值见表4。

图14 V1%式(9)计算值与模拟值对比Fig.14 Comparison between simulated and calculated value of V1%

图14给出了V1%式(9)计算值与本文数模值的比较。

从图14对比结果可见：式(9)的计算值与本文数模值吻合良好，表明了本文对带胸墙斜坡堤单波越浪量影响因素的单因次分析是合理的，分析给出的带胸墙斜坡堤1%单波越浪量计算关系式是可用的，为带胸墙斜坡堤单波越浪量的计算探索了一种可行的途径。

4.3.2 计算关系式验证

下面将通过与已有物模试验结果对比，验证关系式(9)的有效性和计算精度。首先介绍一种式(9)的使用方法：采用《港口与航道水文规范》[12]中带胸墙斜坡堤平均越浪量公式(式(10)所示)计算式(9)中的平均越浪量Q。

(10)

式中：Q为平均越浪量(m3/m/s)；B为经验系数；KA为护面结构影响系数。

范红霞[9]通过物模试验对最大越浪量分布及影响因素进行了研究；本文针对范红霞[9]中适用式(9)的工况，应用规范公式计算平均越浪量Q，带入式(9)计算相应的1%单波越浪量。并与范红霞[9]物模值(本文通过范红霞[2]中的最大越浪量，计算出相应的最大单波越浪量，鉴于其试验波列为120～150个不规则波，可用其最大单波越浪量近似作为1%单波越浪量)进行对比，结果见表5。

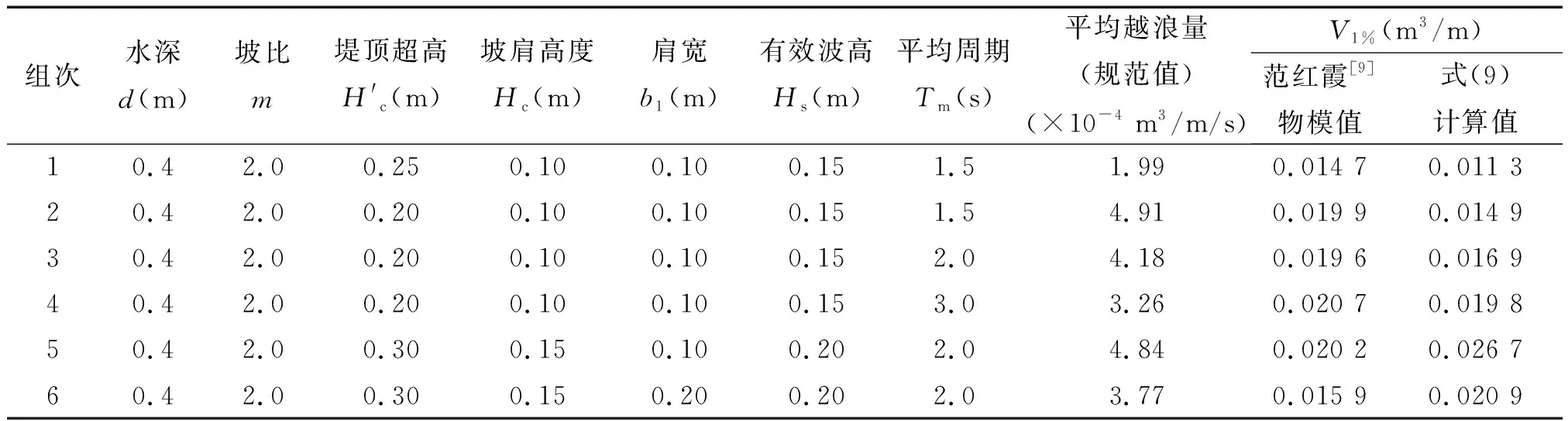
表5 式(9)计算值与范红霞[9]物模值的对比Tab.5 Comparisons between results of formula 9th and Fan Hong Xia[9]

根据表5的对比结果，可见式(9)计算的带胸墙斜坡堤1%单波越浪量与范红霞[9]物模值比较接近，具有较高的计算精度。表明了计算关系式(9)的合理性和计算精度，同时也表明了结合规范平均越浪量公式和式(9)计算带胸墙斜坡堤1%单波越浪量的方法的可行性及准确性，通过式(9)拓展了《港口与航道水文规范》[12]中带胸墙斜坡堤平均越浪量公式的应用方式，使其可用于计算带胸墙斜坡堤1%单波越浪量。以上计算方法可供工程设计时参考和应用。

5 结论

本文借助 FLUENT 软件，采用主动吸收式造波理论，建立了无二次反射的不规则波数值水槽，进行了斜坡堤越浪的数值模拟。通过与已有物模试验结果的对比验证，表明本文数值模式计算的无胸墙斜坡堤平均越浪量、单波越浪量及带胸墙斜坡堤平均越浪量具有较好的计算精度。在此基础上，本文尝试通过数值模拟，分析给出了带胸墙斜坡堤1%单波越浪量的计算关系式，通过公式计算值与本文数模值及已有物模试验结果的对比验证，表明：本文对带胸墙斜坡堤单波越浪量分析探讨的合理性，计算关系式具有较高的计算精度。研究成果可为带胸墙斜坡堤单波越浪量的基础研究及相关工程设计提供参考。