基于原始物理问题 发展科学思维能力①
2018-12-04
(江苏省太仓高级中学,江苏 太仓 215411)
1 什么是原始物理问题与科学思维
原始物理问题基于实际情景,是自然界及社会生活、生产中客观存在且未被加工的物理问题,具有生态性和开放性的特点。原始物理问题不同于物理习题,它们之间的关系如图1所示。

图1
科学思维是人们在认识和改造客观世界的实践活动中总结出来的思维方式和行为方式。科学思维的种类繁多,分类角度不同,结果也就不同,从心理学理论和物理学科特点角度进行分类,结果如图2所示。
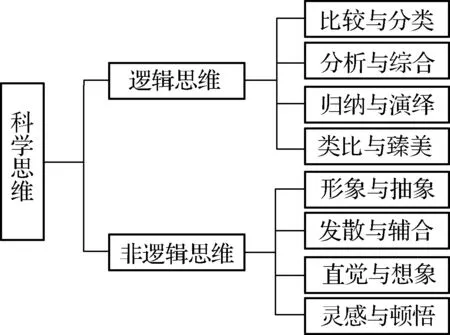
图2
2 为什么原始物理问题能有效发展科学思维能力
2.1 原始物理问题有助于渗透科学思维方法的教育
原始物理问题是基于物理现象的实际问题,没有已知量、未知量和情境图,物理模型需要学生自己去抽象,物理量需要学生自己去设置。因此,学生在解决原始物理问题的过程中要综合应用类比、分析、归纳等逻辑思维方法和猜想、发散、抽象等非逻辑思维方法。
2.2 原始物理问题有助于突出思维过程
因为原始物理问题将活生生的物理现象和物理过程返璞归真地呈现出来,让学生面对原汁原味的物理问题,从而去亲历物理模型、物理概念的形成过程、物理规律的发现过程以及物理问题的解决过程。这些过程是发展物理科学思维的肥沃土壤,也是培育物理学科核心素养的基石。
2.3 原始物理问题有助于显化和内化科学思维方法
研究表明,显化科学思维方法有助于科学思维能力的提升,显化后更重要的是要内化,显化的目的是促进内化。在原始物理问题的解决过程中,蕴含着丰富的科学思维方法教育素材,在解决原始物理问题后,可以通过思维监控的方式,将这些科学思维先显化,再内化,从而有效发展学生的科学思维能力。
3 如何运用原始物理问题发展科学思维能力
在运用原始物理问题发展学生的科学思维能力的过程中,首先,要根据教学内容精心编制原始物理问题;其次,对原始物理问题进行科学建模;再次,赋值解决原始物理问题;最后,通过思维监控内化科学思维方法。
3.1 基于真实生活情境编制问题
编制原始物理问题的方法主要有两种:一种是自下而上的编制方式,即把一些符合标准的习题还原至原始物理问题;另一种是自上而下的编制方式,即对生活中的物理现象、物理问题等进行文字描述,使其成为原始物理问题。不论采取哪一种编制方法,原始问题一定要与真实的生活情境相对应。
3.1.1 自下而上还原
根据原始物理问题和物理习题的关系,如图1所示,把物理习题经过与具体的生活情境对应还原后就可以得到原始物理问题,笔者发现很多物理习题可还原为同一个原始物理问题,可见,原始问题是物理教学的出发点和基石。

图3
例1(2007年全国Ⅱ卷第23题):如图3所示,位于竖直平面内的光滑轨道,由一段斜的直轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动。要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度)。求物块初始位置相对于圆形轨道底部的高度h的取值范围。
类似这样的物理习题有很多,把它们还原后得到的都是过山车问题。因此,应通过原始问题教学,从根本上认识和解决这一类问题。本习题可以还原为这样的原始问题:过山车是一种富有刺激性的娱乐项目,当你在进入“疯狂之圈”之前,过山车先要先从一个较高的坡道上滑下,在通过‘疯狂之圈’的最高点时你对座椅的压力有多大?
3.1.2 自上而下描述
从学生的真实生活背景出发,对一些现象进行描述,就可以得到原始物理问题,也可以创设实验情境,对实验现象进行描述,得到原始问题。
例2:高铁技术是我国的骄傲和“中国智造”的标志,现在很多同学出行首选高铁。在“质点”概念的教学中可以编制这样的原始问题:从上海到北京的高铁需要经过南京大胜关长江大桥,请估算一下高铁列车通过大桥需要多长时间。
3.2 科学建模,发展非逻辑思维能力
由于原始物理问题来自于真实的情景,没有已知量、未知量和情景图,在解决原始问题时首先要对其进行科学建模。分析所研究的问题与哪些因素有关,突出主要因素,忽略次要因素,抓住问题的本质。理清已知量和未知量,并对运动过程进行抽象和理想化处理,建立物理模型,画出情景图,从而有效发展学生的非逻辑思维能力。
针对例1中的原始问题,可以通过“问题串”引导,让学生感知人对座椅的压力大小与哪些物理量有关,进而抽象出运动过程,建立物理模型。
问题1:现在大家坐在凳子上,你对凳子的压力由你的质量决定,当你和凳子一起在竖直平面内做圆周运动时,压力是不是还只与质量有关呢?
问题2:在过山车半径确定的情况下,过山车在最高点的速度大小与什么因素有关呢?
问题3:开始下滑的高度和轨道的粗糙程度如何影响过山车在最高点的速度大小?
问题4:请画出过山车从斜坡上开始运动到圆轨道最高点的过程示意图。
问题5:请在图中标出解决这一原始问题所需要的物理量,用符号表示。
物理习题教学如少了科学建模这一重要环节,也就少了培养学生抽象等科学思维很好的机会。通过问题引导,建立科学模型,构建认知图示。
3.3 赋值解决,发展逻辑思维能力
原始问题的定量解决不同于物理习题,不同点在于:已知量由每个学生自己去赋值,当然计算结果也不同,不追求统一性。这样不仅能激发学生的学习兴趣,更能发展学生的分析、综合和归纳等逻辑思维能力。
针对上述例1中的原始问题,可以通过下面的问题进行引导,促进原始物理问题的解决。
问题1:请根据你的经验估计过山车的轨道半径和在斜坡上开始运动的高度,先假设轨道光滑,根据自己的体重算一算你在最高点时对座椅的压力大小。
问题2:有同学根据自己估计的高度,算出来座椅给人的弹力方向是向上的,想一想有没有生命危险?
问题3:要使人和过山车能安全地通过“疯狂之圈”的最高点,开始下滑的高度与半径之间必须满足什么关系?
问题4:在轨道不光滑的情况下,请估算摩擦力做的功。
学生在估算摩擦力做功时发现:斜面上摩擦力恒定,但进入圆轨道后,摩擦力在变化,此时教师再出手帮助学生。让学生自己赋值,不仅使学生对运动过程的认识更加清楚,还使物理问题生活化,思维更加灵活。
3.4 思维监控,内化科学思维方法
引导学生对原始物理问题的解决过程进行总结、反思和评价,不仅能理清知识脉络,而且能促进科学思维方法的显化和内化。让学生形成自己的思维策略,懂得如何去思考、分析,有效发展科学思维能力。
在“过山车”的问题解决后,进行思维监控,列表显化科学思维方法。

表1 显化科学思维方法
问题1:解决这个原始问题的关键性步骤有哪些?
问题2:这些关键步骤用到了哪些科学思维方法?
可见,在解决一个原始问题的过程中要用到多种逻辑思维和非逻辑思维方法。列出表1后,再通过下面的问题引导促进内化。
问题3:你是怎么想到这些步骤和方法的(对于能解决的同学)?如何才能想到这些方法(对于未能解决的同学)?
基于原始物理问题的教学要放慢节奏,以学生的思维发展情况作为教学的出发点,通过建立物理模型,突出思维过程,通过思维监控内化科学思维,来发展科学思维能力,让学生学会思考、学会学习,有效落实核心素养的培养目标。
