基于北斗和光电平台的无人机单点测距测角的目标定位方法研究

2018-12-04陈海霞左胜甲赵立刚

通化师范学院学报 2018年12期

李策，陈海霞，汉语，左胜甲，赵立刚

早期的目标定位技术可以追溯到20世纪初期，用于提供导航台方位的无线电罗盘出现后，定向器、四航道信标等无线电振幅测向设备也相继问世，另外，还出现了用舰载或机载的测速仪与测向仪结合，推算出舰船或飞机位置的多种算法［1］.20世纪40年代，双曲线定位的近程导航定位系统得到广泛应用［2］.50年代初，应用高频全信标和距离测量设备相互结合构成近程定位导航系统的极坐标系统，能同时向飞机提供相对地面导航台的方位和距离信息［3］.到了70年代，以卫星导航为代表的新型定位系统陆续出现，随之而来的多种组合定位方式为以后定位技术提供了一条发展之路.

随着应用光电平台对目标进行定位测量系统的相关技术在各个领域应用越来越广泛，基于光电探测设备的相关产品逐步具备了完成高精度侦察目标定位任务的基本硬件条件.本文研究基于高精度北斗定位和双天线寻北定向的方法，设计单点测距测角的目标定位方法，并且以“翼龙”无人机为模型，对目标定位方法进行误差分析.

单点测距测角的目标定位方法是在某一点利用无人机的光电平台采集目标的距离和角度信息，返回无人机综合处理器对目标进行实时定位.在实际应用中，此技术依赖于机载光电平台的图像识别跟踪技术以及各种仪器测量技术.

无人机到达目标区域范围后，通过机载光电平台图像系统识别目标，并且完成对目标的闭环跟踪.随后进入测量阶段，无人机在某点测量时，测量出无人机此刻的自身位置、北向角、姿态角、光电平台的转角、无人机与目标的距离.随后将测量信息返回无人机中的综合处理器，通过定位算法，完成对目标的实时定位，详见图1.

图1 无人机测距测角定位示意图

1 北斗定位和双天线寻北定向

1.1 北斗定位

北斗卫星定位的基本原理是测量出已知位置的卫星到用户接收机之间的距离，然后综合多颗卫星的数据来确定接收机的具体位置.为达到目的，卫星的位置可以根据星载时钟所记录的时间在卫星星历中查出.而用户到卫星的距离则通过记录卫星信号传播到用户所经历的时间乘以光速得到［4-6］.

考虑到一般通用性，无人机在飞行过程中的定位数据仿真中采用单点的定位方式，根据目前高精度的北斗接收机单点定位精度能够达到2.5m，若是在有地基增强站的情况下，采用差分定位方式精度可达到亚米级.

1.2 双天线寻北定向

利用北斗接收机双天线可以完成对于两个天线基线的寻北定向，在理论上运用两个天线不仅可以完成寻北定向而且可以完成对于无人机自身的俯仰角测量.所以，为了简化系统，无人机姿态测量也采用北斗卫星的测量方式.

双天线寻北利用接收机天线的载波相位差分，先求单差和双差.单差观测是指两个接收机对同一颗卫星i同步载波相位观测值取差，有

双差指在单差的基础上，不同卫星i，j之间再作差

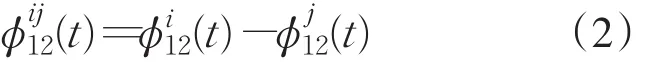
式中，ϕ(t)=ρ-λN+υ，λ是载波波长，ρ=λ(φj-φi)为星站之间的距离，N为整周模糊度，υ为观测噪声.

天线1到天线2的距离远远小于导航卫星之间的距离，所以此时一般把不同卫星到两个天线之间的距离当作相同，此时两天线的载波相位差分观测方程为

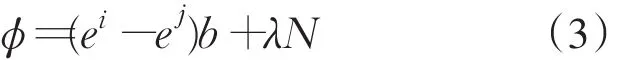
式中，ei和ej分别表示天线到卫星i和卫星j的单位方向矢量；b=[x，y，z]T为在当地地理坐标系下的基线向量，详见图2.

图2 双天线寻北

假设观测到n颗卫星，则可以得到n组基线矢量坐标，得到观测方程：

上述方程有两组未知数需要求解，一组是(x，y，z)，另一组是整周模糊度.

将双天线分别放置在无人机的两端，则两天线基线坐标在载体坐标系下为：

根据卫星接收机得到两天线在载体坐标系下的位置分别为b1=[x1，y1，z1]，b2=[x2，y2，z2].设俯仰角为ε，横滚角为γ，北向角β.根据上面提到的旋转转换矩阵，得到有关北向角β的关系式：

其中，Rβz为绕z轴的旋转矩阵，Rεy为绕y轴的旋转矩阵.将矢量坐标带入上式：

由三个方向的旋转矩阵及基线向量关系，得

带入ε和β入上式，得到横滚角

2 目标定位解算

本文所采用的目标定位解算方式如图3所示，具体步骤如下：

第1步：初始状态.

由于基于北斗系统的定向是测量无人机上安装的两个天线的基线与北向的夹角，但是测量时所需要的夹角是光电平台的图像镜头（或者认为重合的激光测距机）与北向的夹角.所以在初始状态需要在水平面上调整光电平台镜头使之与寻北的双天线基线保持一致，方便后面的解算.

图3 目标地理坐标计算示意图

在计算中，忽略无人机北斗定位与光电平台自身位置的定位误差，将北斗系统对无人机位置的测量值当成光电平台位置值，且认为光电平台的载体坐标系与无人机平台的载体坐标系一致.

第2步：在无人机飞行过程中完成目标稳定跟踪后，选择测量时刻.在测量时刻，测量目标与无人机的距离为R，图像镜头在水平和俯仰相对于初始状态转过的方位角和俯仰角角为α、λ，求出目标在载体坐标系中的坐标值（Xb，Yb，Zb），则

其中，α，λ，R为测量得到的目标与载体坐标系的相对方位角、俯仰角测量值及相对的距离测量值.

第3步：采用齐次坐标转换的方法，求出载体坐标系到大地直角坐标系的转换矩阵；

其中，C为大地直角坐标系与地理坐标系的转换矩阵.

其中，αs，λs，hs分别为光电探测设备的大地经度、纬度和高度，e为地球参考椭球的第一偏心率，RN为卯酉圈曲率半径.

C为地理坐标系到载体的变换矩阵：

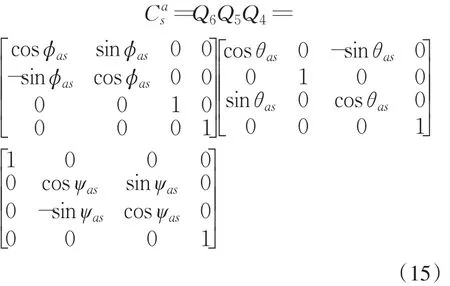
其中，ϕas，θas，ψas分别为光电探测设备的横滚角、俯仰角和北向角.

第4步：完成大地直角坐标系到大地坐标系的转换，即求出目标在大地坐标系中的经度B，纬度L和高程H.目标经度为：

目标纬度L和高度H可以利用迭代法求取，取迭代初值为：

直至

其中，ε1，ε2按所要求的精度决定，一般取值0.1.

最后求得的目标在大地坐标系下的坐标（B，L，H）即为最终定位结果.

3 误差分析

在对目标的定位过程中，由于存在很多的测量过程，以及无人机在飞行中存在姿态的误差，导致整个定位过程中存在众多的随机误差和系统误差.

3.1 无人机目标定位误差源分析

在单点无人机进行目标定位时，误差源主要来源于表1.

表1 误差源

目标定位方法的误差均属于测量误差，在目标定位误差方程中，带入各参数的名义值和其相对应的误差值，这些参数的误差分布基本属于正态分布.

目标定位方程中，要获得各参数对计算结果的影响，首先要建立误差传递方程，运用蒙特卡洛法获得的数学模型为xi为各参数的测量真实值，Δxi为测量误差，F代表定位过程.

本文误差分析采用蒙特卡洛误差分析方法，步骤如下：

（1）在MATLAB软件中输入定位过程中使用的各个参数变量的真实值，并计算出无误差情况下的定位结果.

（2）输入各个参数误差的均方根值；

（3）使用randn（）函数，生成还有误差的各个参数变量的随机序列；

（4）运用蒙特卡洛方法进行模拟仿真，计算含有误差的目标定位结果；

（5）重复以上方法对目标的定位进行多次循环仿真，对定位结果进行统计输出并分析.

3.1.1 激光测距机误差

激光测距产生的误差主要来自两个方面：一是距离测量的误差；二是激光测距机与光学镜头的光轴一致性的误差.

现代光电平台中己经普遍采用固态激光测距机，激光测距机原理是激光器产生高能激光，对准目标进行发射后，通过计算激光回波与激光发射的时间差乘以光速，即可得到激光器与目标的距离.激光测距机有采用相干测距和非相干测距（普通）两种方式，其定位精度也不同，详见表2.

表2 激光测距机性能

通常无人机机载光电平台均设计为可见光摄像机与激光测距机独立光路，即可见光摄像机与激光距机是两个独立的设备，独立安装于光电平台的内框架.由于光电平台内框架安装基面的加工误差，可见光摄像机的安装基面的加工误差、激光测距机安装基面的加工误差，内框架变形等因素，造成可见光摄像机与激光测距机安装在平台内框架后，光轴不能完全平行，此情况带来的定位误差也会累加在激光测距误差里，如图4.

图4 光轴不一致

3.1.2 光电平台转动误差

在对目标位置进行解算时，需要知道光电平台自身转动的角度.目前，主流的光电平台通过装配在方位轴系上和俯仰轴系上的角度编码器测量目标在平台坐标系下的转动的角度.当光电平台的光轴对准目标时，光电平台编码器俯仰角、光电平台编码器方位角.由于编码器自身分辨率精度、重复性、光电平台的编码器安装面不平整、编码器轴与光电平台的轴不完全重合等因素，造成方位角、俯仰角编码器测量误差，如图5所示.

图5 角度编码器

除了角度编码器，还有应用IMU等其他测量设备对光电平台转角进行测量的工具.目前常用的高精度光电平台转角精度测量可以达到0.2mrad，相对于北向角测量误差显得很小.

3.1.3 北斗系统双天线寻北定向误差

（1）误差公式分析.在第（3.1）小节中，推导了通过北斗接收机三天线的方法进行寻北定向和无人机姿态角的测量.

对式（8）进行微分，得到

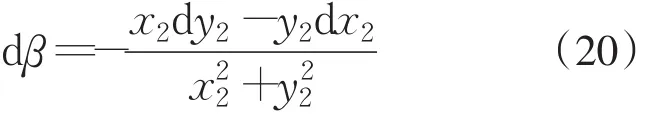
得到北向角误差：

同理，对无人机的俯仰角和横滚角进行微分，得到俯仰角和横滚角的误差分别为：

由此可见，无人机北向角、横滚角和俯仰角都与基线长度呈反比，在无人机上的三个基线两两越远则越有利于无人机姿态角的精度提高.

（2）姿态角误差仿真.传统的光钎陀螺寻北仪目前的寻北定向精度在1密位（约0.06°），本文所提出的利用北斗多天线寻北能否具有使用价值则取决于误差因素.通过不同基线长度的仿真，得到三个角度的误差如表3.

表3 双天线寻北误差

总体上看，双天线的基线长度与定位误差呈反比关系，随着基线长度增加误差收敛减慢，趋于平缓.在基线长度达到9m时，北向角的测量误差接近传统光纤陀螺寻北仪的定向精度.我国翼龙无人机，机身长度11m，若是在机头和机尾分别安装用于寻北的天线，则在无人机可以达到高精度的寻北.但是由于测量横滚角的基线长度取决于机身高度，目前无人机的机身高度不会高于4m，所以横滚角的测量在此方法中会相对较大.将上表绘制成图像，如图6.

图6 基线长度与寻北姿态误差

3.2 误差分析与仿真

本节分析的误差的来源主要来自于三个方面：一是采用双天线对无人机寻北定向；二是激光测距机对目标的测距；三是无人机自身的位置精度.根据上面的定位公式，目标在大地坐标系下与各个测量量的关系为：

下表列出了定位过程中，本章所分析误差源参量的模拟值、误差值及各变量误差服从的概率分布情况如表4、表5、表6.

表4 误差源仿真数值

表5 数据来源

仿真数据说明，无人机位置误差（纬度、精度和高程）来自于成都通航公司所产3040型接收机的单点误差参考值，位置的信息来自于成都市的纬度、精度和海拔高程.无人机的北向角、俯仰角和横滚角数据来自于北斗三天线进行寻北测姿时的仿真数据，无人机机身长度参考中国“翼龙”型无人机，模拟无人机在飞行过程中与地平面保持水平平稳飞行.光电平台的俯仰角和方位角参考一般数据.激光测距机测距参考“翼龙”型无人机的测距作用范围.

表6 其他分量仿真值

本文误差分析中，没有对无人机的俯仰角和横滚角进行误差分析，目前的机载光电平台往往是独立于机体，即机体的微小俯仰和横滚转动不会影响光电平台的姿态，在本文的模型中，将无人机载体与光电平台载体坐标系简化为一体，所以认为在定位过程中无人机一直保持平稳.

在无人机机载光电平台目标定位过程中，表中各个定位用参数相互独立，所以，采用控制变量法分析单个参数与定位结果的对应关系，分析定位结果的误差同各变量之间的关系，即只改变以上参数中的某一个参数的真实值或误差值，其他变量的名义值或误差值不变，由此得出这个参数或其误差对定位精度的影响.利用MATLAB软件，通过误差图直观地表现各个误差源对定位精度的影响.

（1）无人机测距误差对定位精度的影响.在定位误差中只加入激光测距机的测距误差，其他仿真数值采用表中的数据，激光测距定位误差采用非相干激光测距的3m误差，得到定位误差和误差值分布图（如图7所示）.

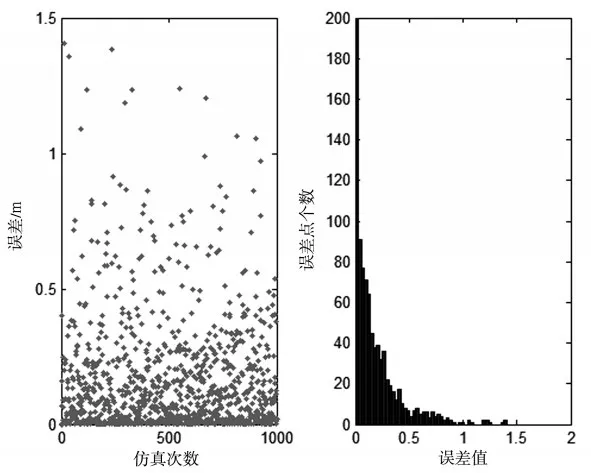
图7 误差值及分布

定位误差的均值为1.583m.在定位公式中可以看出，激光测距的误差对于整个定位精度的影响较小，在定位过程中不是主要的误差源.

（2）无人机寻北对于目标定位的影响.在其他误差源不加入误差的情况下，只加入由于双天线基线长度为9m时，寻北定向导致的北向角误差，误差为0.0621°，得到误差结果如图8.

图8 误差值及分布

通过计算，定位误差的平均误差为25.6m，与激光测距误差相比，北向角误差对于定位误差的影响较大.

（3）基线长度与激光测距对目标影响.

图9 基线长度、测距与定位误差关系

经过误差仿真，如图9，可以看出，随着双天线基线长度的不断增加，定位误差大幅度增加，激光测距的误差随着基线长度的增加对定位误差的影响不明显.双天线基线从9m到1m的仿真中，定位误差从20m增加近2000m.在双天线架构基线小于过5m时，则定位误差会超过100m.所以在本文设计的基于“翼龙”型无人机的双天架设中，尽量选择远距离的双天线架构.

（4）加入全部误差源后的目标定位误差.对表4中的误差源全部带入，观察在本节所提的定位方法中目标定位的精度值.

在加入无人机自身定位误差、9m基线时的寻北误差和激光测距误差后，定位的平均误差33.563m，结果如图10所示.

图10 误差值及分布

（5）无人机不同位置时误差情况.本方案设计的误差仿真分析仅对北纬度30.5°，东经104°，高程为3600m的一个孤立点上（本文所述孤立点为无人机单独的位置点），对所设计的单点测距测角定位进行误差分析.基于此，模拟无人机在北纬0°到90°，步进为10°；东经0°到180°，步进为20°；高成为3600m的100个点，采用本文所述的双天线寻北9m基线、激光测距为5km，且误差源分布服从表4时，各个位置的误差情况.