点阵结构空气舵及内部流体热流固耦合研究

向 羽，刘 彬，张树哲，李俊峰，魏 培，魏正英

(1. 西安交通大学机械制造系统工程国家重点实验室, 西安 710049；2.北京宇航系统工程研究所，北京 100076)

0 引言

空气舵是高速飞行器飞行控制系统的执行机构和关键部件，工作环境异常严酷，舵轴使用载荷要求在1300℃高温环境下达到3200N·m，其气动加热效应相当严重。随着飞行器性能指标的不断提高以及服役环境越来越苛刻，飞行器结构设计和材料选用向轻质化、高性能化、整体化、结构功能一体化的方向发展，复杂型面薄壁结构和变截面内流道结构越来越多，高性能但加工困难的钛合金使用越来越广泛，现有的制造技术体系面临的挑战也日益严峻[1]。近年来，激光增材制造技术逐渐成熟，为解决上述关键金属构件的制造难题提供了新的途径，可望为航天领域制造业的发展带来革命性的变化[2]。

在此背景下，结合增材制造技术，研究轻质、散热及高强韧的多孔轻质结构的先进新型空气舵具有广阔的前景[3]。点阵结构是一种新型多孔材料，具有优异的散热和力学性能，目前国内外学者对点阵结构的流动及传热特性进行了研究，如Evans等[4-5]和Hutchinson等[6]通过数值传热学分析了点阵结构的散热特性;Mohr等[7]运用介观力学的理论，构造了点阵结构的非线性行为本构模型； Dostert等[8]把点阵结构的流道看作多孔介质，用有限单元法(FEM)研究了多孔介质的流动及传热特性；卢天健等[9-10]和罗树坤等[11]通过流固耦合共轭传热数值计算方法，获得了流体与结构的三维瞬态温度场，并通过顺序耦合求解获得了结构的应力场。然而，将点阵结构应用于空气舵结构中缺乏严谨的科学验证，点阵结构的空气舵与热服役之间的耦合关系及热结构响应需要进行深入研究。

当前，金属增材制造技术如激光粉末床熔融(LPBF)技术仍需要在制造件的致密度、强度以及疲劳性能等方面开展相关研究。为此，针对空气舵制造要求的高精度、结构功能一体化等特点，本文采用LPBF技术作为研究对象，采用空气舵加工常用的TC4材料，通过对LPBF技术工艺的研究，并结合LPBF工艺，设计了传统工艺难以制造的点阵结构空气舵，并且采用基于有限差分法(FDM)计算流体力学模拟验证的方法对点阵结构空气舵的防热特性进行研究。在外加热流通量的情况下，冷却液(水)通过流道，与冷壁面热流固耦合共轭传热。计算过程中考虑了水和钛合金材料的热物性参数随温度的非线性变化行为及湍流换热特性，采用顺序耦合求解进行热分析。冷却水流动过程中的自由界面采用流体体积法(VOF)，用来追踪流动过程中的自由界面。得到了满足空气舵服役条件的LPBF工艺和冷却液添加的入口条件，为下一步开展结构功能一体化的点阵结构空气舵防热实验奠定了基础。

1 实验材料及方法

1.1 设备与材料

采用自主研发的SLM-300设备开展相关实验，使用德国TLS公司生产的TC4粉末作为实验材料。图1是在扫描电镜(SEM)下观察到的原始粉末形貌，大多数粉末颗粒呈球形状，这有利于提高铺粉的均匀性和熔池的润湿特性。粉末化学成分如表1所示。该粉末是将高纯合金棒料经气雾化方法制备而成，粉末成分均匀，粉末粒径分布在15μm～53μm之间，粉末粒径分布服从正态分布，粉末的累计粒度分布百分数达到x%时所对应的粒径，x=10、50、90，D10=21.30μm，D50=32.42μm，D90=49.25μm，粉末平均粒径为33.55μm。

表1 TC4化学成分

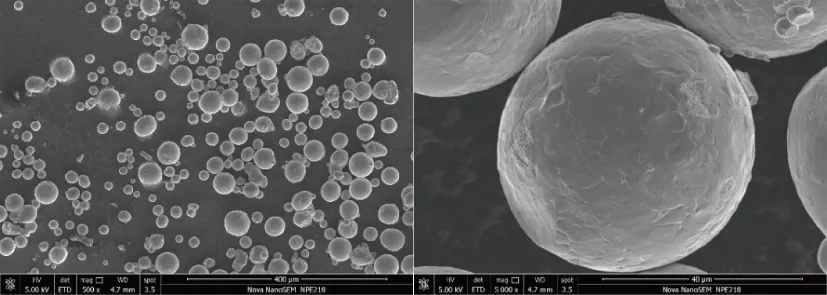
图1 TC4粉末的SEM图像Fig.1 SEM images of TC4 powders

1.2 试件制造及性能测试

1.2.1 单道实验研究

围绕扫描速度(v)、激光功率(P)两个参数,确定成形材料TC4的单道基本成形工艺参数窗口，如图2所示。激光功率取值范围为200W～380W，扫描速度取值范围为1200mm/s～3800mm/s，线能量密度E=P/V，取值范围为52.6J/m～316.7J/m，单道成形后，观察各单道的成形形貌，将其划分为成形单道过宽、成形正常、单道不规则及单道不连续等4个种类。成形单道过宽，是由于扫描速度低能量密度大，单位时间内粉体接收能量多，导致熔池成形过宽，同速度下，随着功率的增大熔道变宽；单道不规则，是由于随着扫描速度的增加，激光输入能量不足，导致单道成形呈现出葫芦状，随着速度的再度增大，出现断续、未熔的现象。正常的单道形貌呈现前后熔合匀称，熔宽略大于激光光斑，与基板的熔合角度约90°，从图2中得知，较优的成形工艺参数为：功率为280W～320W，扫描速度为1800mm/s～2200mm/s。

图2 单道成形工艺窗口Fig.2 Single track forming process window

1.2.2 致密性研究

设计工艺实验开展致密化研究，实现高致密TC4成形，工艺实验所用参数如表2所示。实验过程中扫描填充策略为错层扫描方式，如图3(a)所示，成形块体为立方块体，如图3(b)所示，铺粉层厚为固定值0.03mm。

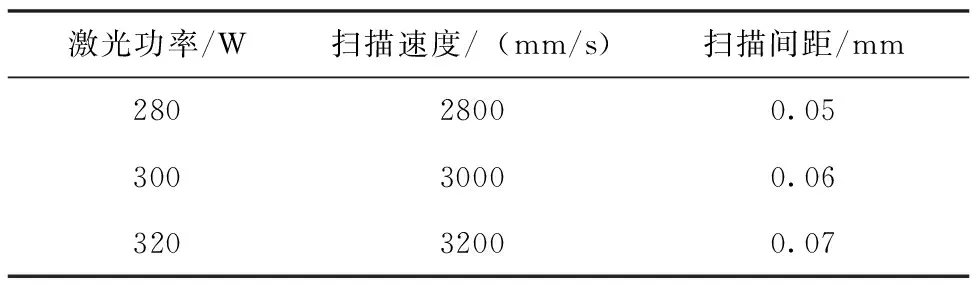
表2 工艺参数

(a)扫描填充策略 (b)成形块体 图3 扫描填充策略及成形块体Fig.3 Scanning filling strategy and forming block

定义体能量密度表征致密度变化规律。体能量密度表达式如式(1)所示。

V=P/(v·h·t)

(1)

式中，体能量密度为V，单位J/mm3；激光能量为P，单位W；扫描速度为v，单位mm/s；扫描间距为h，单位mm；铺粉层厚为t，单位mm。

基于阿基米德原理，采用排水法测量样块致密度(相对密度)，得到致密度随体能量密度变化规律，如图4所示。

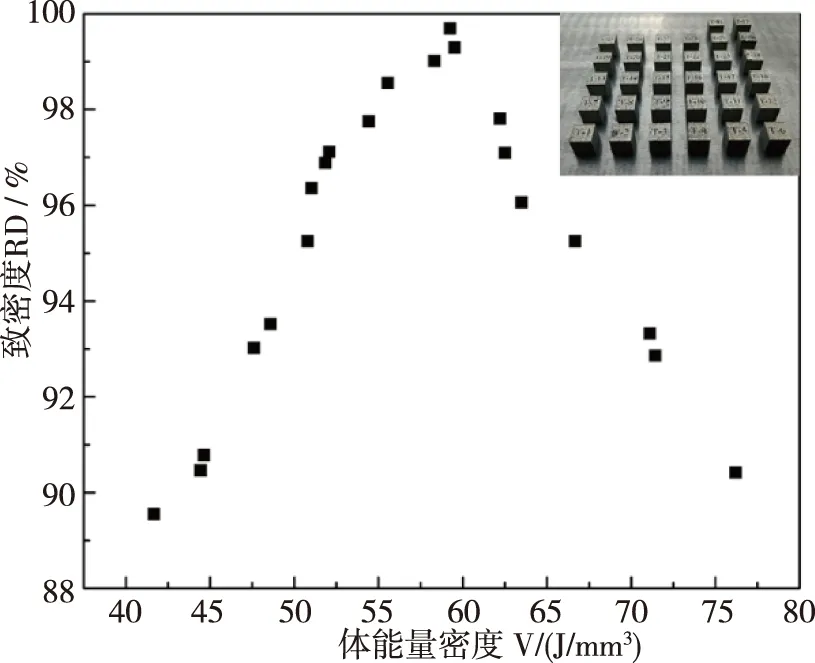
图4 致密度随体能量密度变化规律Fig.4 Change of density with volume energy density

从图4可以看出，随着体能量密度的逐渐增加，样块的相对密度呈先上升后下降趋势，可以得到相对致密度较为优化的工艺参数区间为V=55J/mm3～62.5J/mm3。

2 增材制造模型设计及流固耦合分析

2.1 模型设计及成形可行性验证

首先进行空气舵的结构CAD结构设计，整体外形按照一般空气舵外形设计，底面最大长度为332mm，顶面最大长度为234mm，模型最大宽度为30mm，高度为170mm，其整体结构如图5所示。其中舵芯内部结构为空结构，舵芯和外部蒙皮之间采用如图6所示轻质点阵夹心结构构成复杂的流向结构连接。空气舵下端为进水口，冷却水由此进入。舵芯四周和蒙皮之间的空腔形成流道，蒙皮上设计有流道出口，每一面设计25个直径1mm的出口，根据空气舵使用要求，冷却水由流道出口以发汗形式流出。

图5 空气舵三维结构Fig.5 Air rudder three-dimensional structure

(a)排列 (b)单个图6 轻质点阵夹心结构Fig.6 Lightweight lattice sandwich structure

采用较优工艺区间V=55J/mm3～62.5J/mm3中的激光功率300W，扫描速度3000mm/s、扫描间距0.06mm以及铺粉层厚0.03mm进行的空气舵(部分)的打印，如图7所示，可以看出制件成形质量良好并且表面致密，表明了通过工艺研究找到优化工艺区间的可行性。

图7 空气舵LPBF工艺打印件Fig.7 Air rudder by LPBF

2.2 物理模型及计算模型

2.2.1 流动计算主控方程

空气舵内流体流动受三大物理守恒定律的支配，即质量、动量和能量守恒定律。

2.2.2 湍流模型

模型中的流体假设为不可压缩牛顿流体，点阵结构中的流动形态比较复杂，呈现出湍流的特性。大量的理论和实践经验表明，标准的k-ε湍流模型具有很好的稳定性、经济型和高精度，在复杂流道模型的湍流计算中得到广泛的应用[12]。因此本文湍流模型采用k-ε模型,如式(1)～式(2)所示：

(1)

CεlPk-Cε2ρkε2

(2)

计算中，取

σk=20,σε=1.4,Ck1=1,Ck2=0.09,Cε1=0.555，Cε2=0.83，Cμ=0.09。

2.2.3 空气舵内流道传热计算模型

外壳传热：

Q=WsCp(Tout-Tin)

(3)

式中，Ws为流体的质量流量，Cp为流体的定压比热容，Tin、Tout分别为流体进、出温度。

空气舵的传热系数：

h=Q/(A·ΔT)=Q/[A(Tw-Tb)]

(4)

式中，A为传热面积，Tw为壳体壁面温度，Tb为定性温度。

管程传热系数：

(5)

式中，Qtube为传热量，Atube壁为面积，Tf、Tw分别为流体温度和壁面温度。

为了提高计算模型精确度,得到更加符合实际情况的计算结果,水的动力黏度μ和导热系数λ如图8所示。

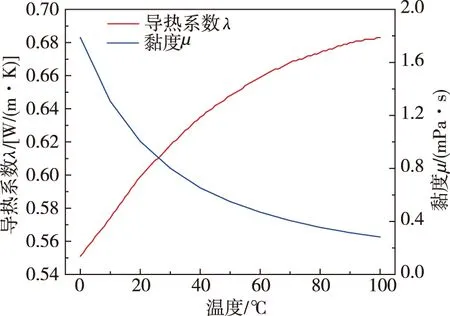
图8 水的导热系数及动力黏度Fig.8 Thermal conductivity and dynamic viscosity of water

2.2.4 VOF方法

空气舵内部流道中的液面与空气的边界为自由界面，而冷却水在高温下发生蒸发，此时对于两相之间的界面捕捉是一个难题。本文采用VOF方法，对蒸发冷凝、表面张力、界面传热传质、对流传热传质等进行计算[13]。

2.2.5 计算模型及边界条件加载

模型输入CFD软件FLOW3D中作为计算的几何模型，如图9所示。模拟过程中，空气舵为实体模型，工作介质为水。空气舵下圆孔为速度进口(velocity inlet)，进口初始速度v0为2m/s～4m/s，初始温度T0为20℃，初始时刻水的比热容Cp1随温度变化可忽略，因此可定义为4191(J/kg·K)。

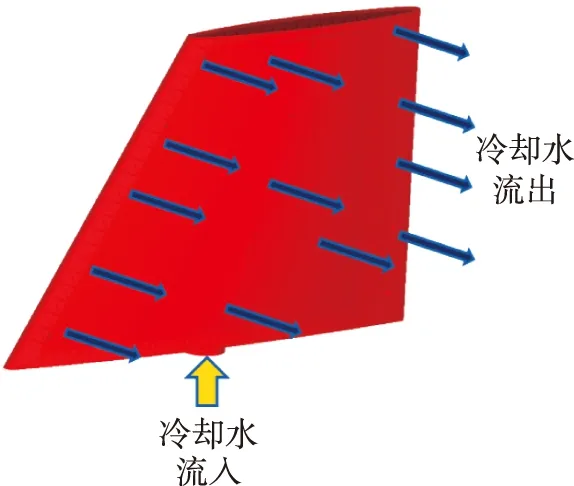
图9 空气舵计算流体力学的CFD几何模型Fig.9 CFD geometric model of computational fluid dynamics for air rudder

壁面和流体为无滑移边界条件，外蒙皮与舵芯间充满水，水在压力下以发汗形式流出空气舵，其出口设置为压力出口条件(pressure outlet)，出口压力为常压。外蒙皮为墙体(wall)，加载热流密度qe的值由实验得到，取均值20kW/m2。求解方式采用瞬态求解，湍流模型采用标准k-ε模型。冷却水液相的密度ρl和沿着界面的两相表面张力σ均认为是与温度T相关的函数，分别由式(6)、式(7)确定(CGS单位制)[14-15]：

ρl=-0.0022T2+0.9237T+919.8

(6)

σ=-2.3×10-7×T2-1.845×10-5T+0.09805856

(7)

空气舵外蒙皮为钛合金(TC4)，并且温度不能超过钛合金的熔化温度，固态的钛合金密度随温度的变化不大，故钛合金蒙皮的密度可以视作常量，ρTC4为4.44×103kg/m3，而热导率km2(W/m·K)和比热容Cp2(J/kg·K)均认为是与温度T相关的函数[16]，分别由式(8)、式(9)确定。

km2=1.2595+0.0157T

(8)

Cp2=483.04+0.215T

(9)

2.3 结果与讨论

由于整体模型的复杂性，要保证计算的精确性，其整体计算网格在1亿以上，并且计算过程中存在汽化蒸发、湍流等现象，求解过程中，迭代时间步长在10-16s左右。如果取整体计算，会大大降低计算效率，如图10所示，计算1s时间，耗时一周，如果采用整体模型结构计算寻找规律，耗费时间，效率非常低下。

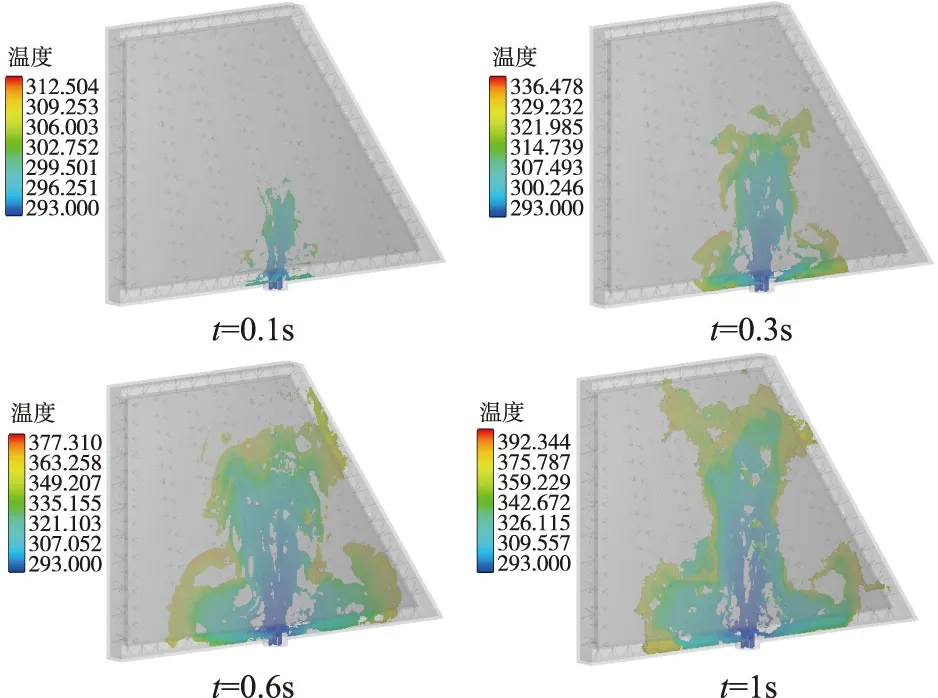
图10 1s内的水在空气舵中的发展流动过程中冷却水温度分布Fig.10 Temperature distribution of cooling water in the development of air rudder within 1 second

空气舵内部由于靠近出口段的入口速度及蒙皮出口的压力最大，充分发展时，若出口处的速度和压力满足设计要求，可以认为空气舵的设计满足要求。而对温度的研究也一样，采用分段求解的方法，取通道的一段作为研究对象，计算的数据结果可以作为下一段的计算入口，最终可以得到每段通道流场中的温度、速度、压强分布情况，如图11所示。模拟中采用heat transfer求解器，设置时间步长10-16s，计算模型通过收敛性验证。

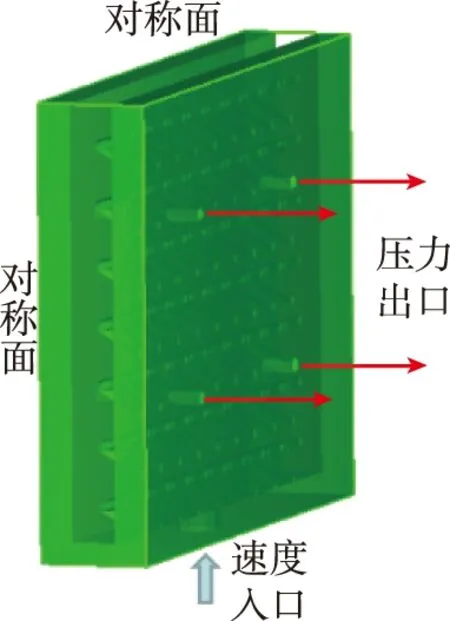
图11 局部分段计算模型Fig.11 Partial segment calculation model

2.3.1 压力分布

首先截取入口段40mm×60mm作为研究对象，入口采用速度入口，水流速度为0.4m/s～2m/s，出口采用压力出口边界条件，其他段采用对称结构，研究水流速度对空气舵出口的压力影响。实体表面加载20kW/m2的热流密度，计算过程单位采用cm。

冷却水填充空气舵是一个过程,但是研究水流速度对空气舵出口压强的影响规律，需取冷却水充分充填时的压强进行研究，取入口速度为0.4m/s、0.8m/s、1m/s和2m/s的速度入口条件，即图12中1.2s时的情况进行比较。

由图12可以看出，不同的入口水流速度，将产生不同的出口压强。当入口水流速度为2m/s时，出口压强将达到2MPa(计算采用的CGS单位制)。随着入口水流速度的降低，内部压强逐渐降低，当入口水流速度为0.4m/s时，内部压强只有0.12MPa～0.13MPa。根据空气舵的服役要求，在空气舵工作时，水流须以发汗的形式流出，不能形成水柱。当入口速度为2m/s时，出口压强高达2MPa，高压情况下，容易形成水柱，不符合空气舵工作的要求。

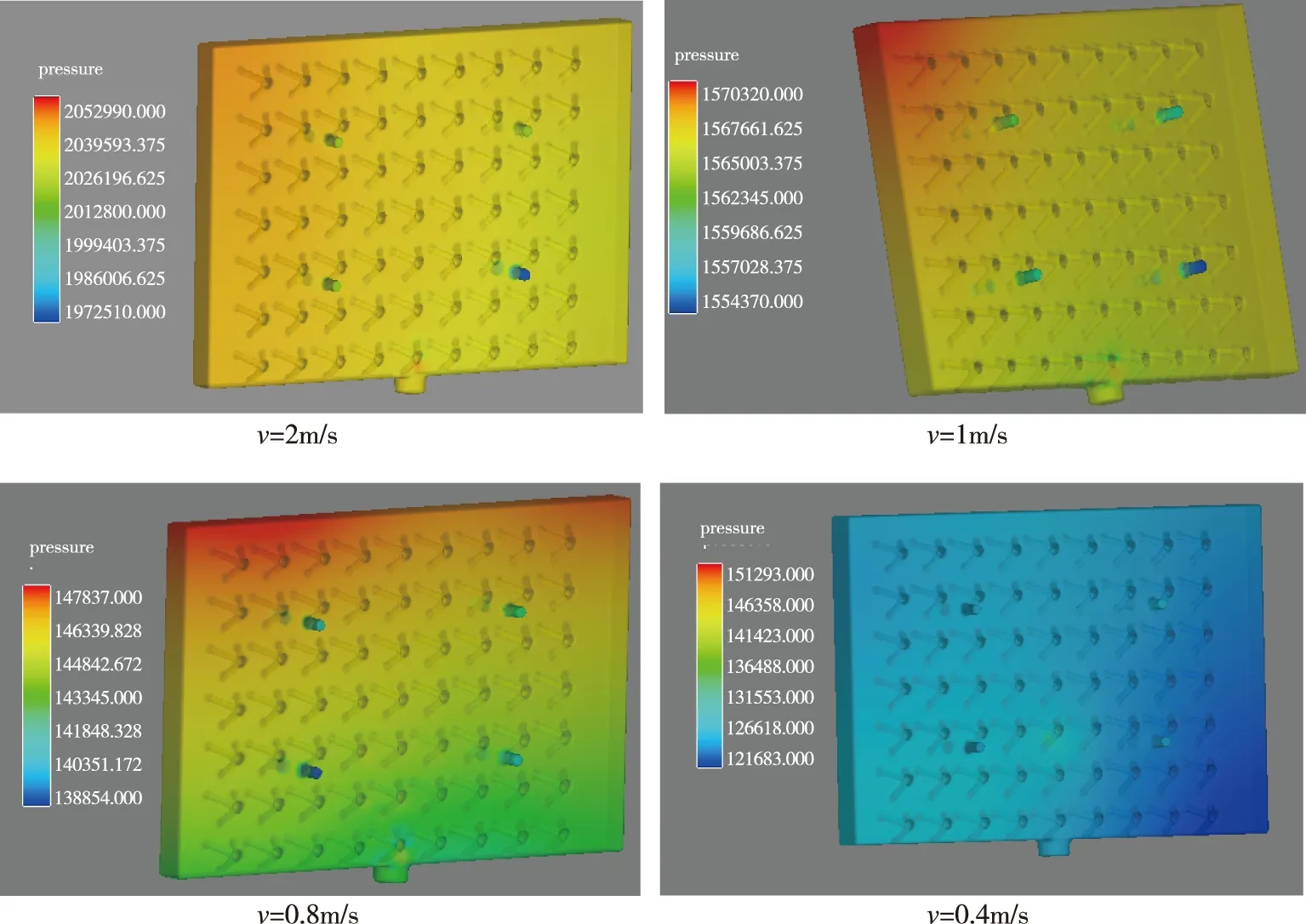
图12 速度对空气舵出口压强的影响Fig.12 Effect of velocity on outlet pressure of air rudder

2.3.2 速度分布

不同的内部压强将对出口的水流速度产生影响，研究入口水流速度为0.4m/s～2m/s时，入口水流速度对出口速度的影响，如图13所示。

由图13可以看出，当入口水流速度为2m/s时，出口速度达到3m/s～3.5m/s(计算采用cm)。随着入口水流速度的降低，出口速度逐渐降低，当入口水流速度为0.4m/s时，出口速度只有0.35m/s～0.55m/s。

当出口液体流速过大时，空气舵出口的水流将产生一个水柱喷出，如图14所示。出口的长度为4mm，计算区域为2cm，当出口压强为2MPa时(外部压强设置为0.13MPa)，出口速度为3m/s左右，在计算区域内，为一条水柱。空气舵的要求为水要以蒸汗形式流出，即出口速度应该很小，可以通过控制入口水流控制出口水流压强，获得较小的出口速度。

图15显示当水流入口速度为0.4m/s时(此时出口压强为0.131Mpa)，出口的速度为0.5m/s左右，此时水柱若只在重力影响下时为1cm左右；而当空气舵实际工作时，由于重力加速度的作用，水流几乎是贴着外蒙皮流出，可以认为是以蒸汗形式流出。

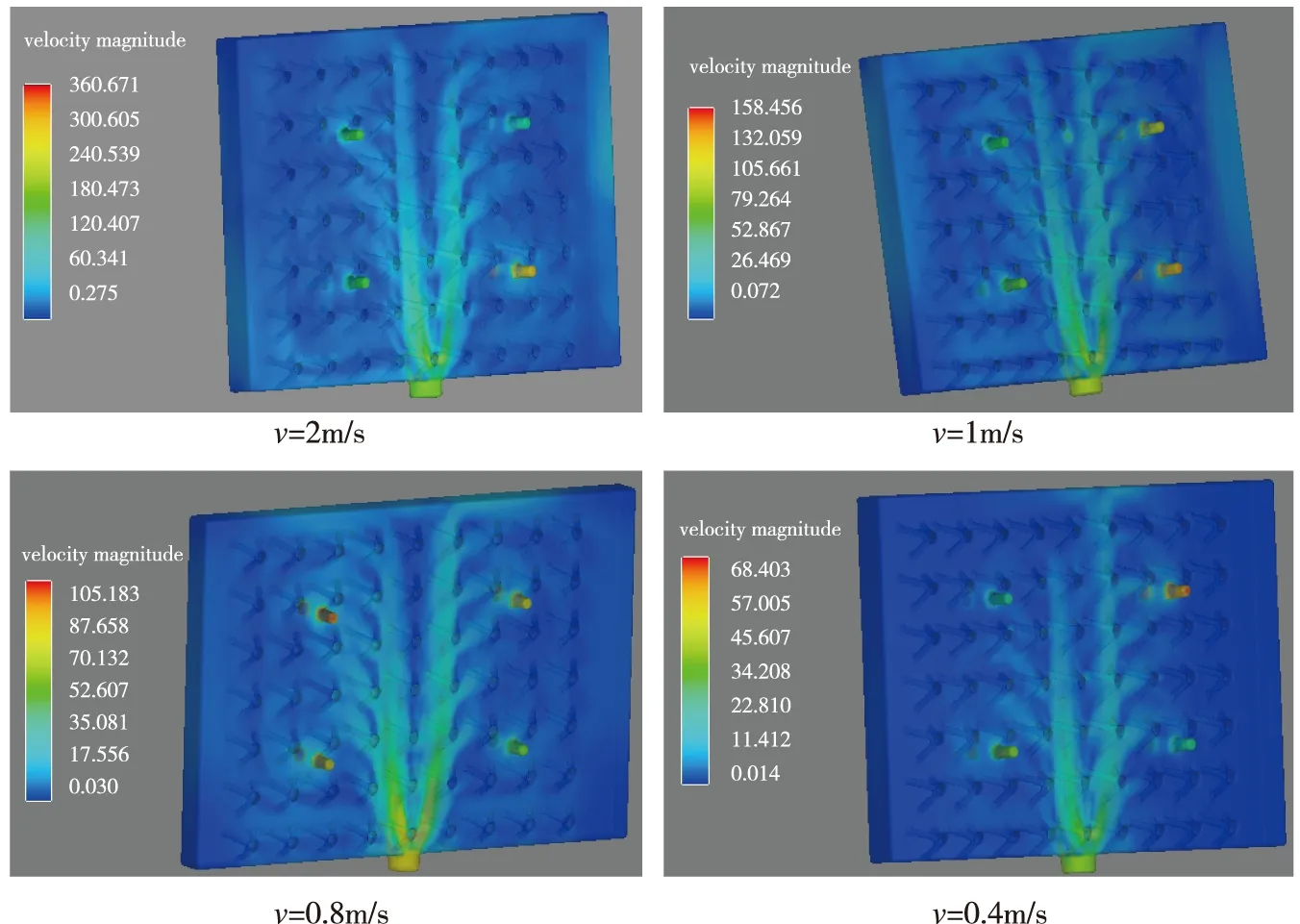
图13 入口水流速度对出口水流速度的影响Fig.13 Effect of inlet velocity on outlet flow velocity

图14 出口压强为2MPa时的出口速度Fig.14 Exit velocity at outlet pressure of 2MPa

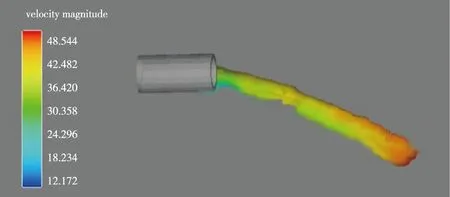
图15 出口压强为0.131Mpa时的出口速度Fig.15 Exit velocity at outlet pressure of 0.131Mpa

2.3.3 温度分布

水对壁面的影响也是一个逐渐降温的过程。冷却水流出的同时带走大量的热量，从而冷却外壁面，以入口速度为2m/s时为例，如图16所示的壁面温度分布，0.2s时内壁面的最低温度为730.458K，而1.2s时(图17)刻内壁面的最小温度已降到669.502K (396.502℃)，降温效果比较明显，下降温度为60.956K。

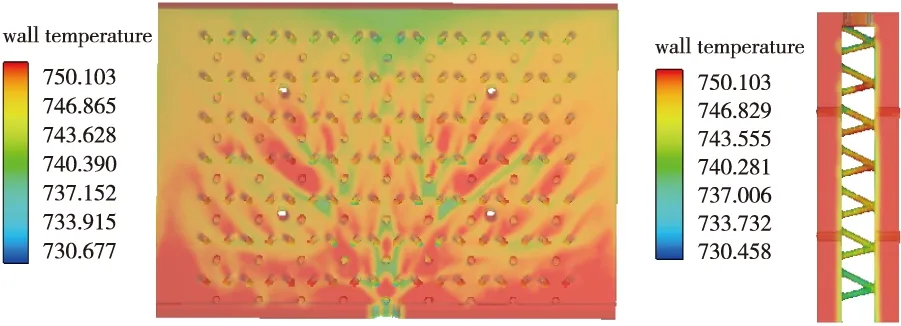
(a)轴向 (b)径向 图16 蒙皮外壁面的温度随时间0.2s时刻的分布情况Fig.16 Distribution of temperature on the outer surface of the skin with time 0.2S

(a)轴向 (b)径向 图17 蒙皮外壁面的温度随时间1.2s时刻的分布情况Fig.17 Distribution of temperature on the outer surface of the skin with time 1.2s

不同的入口水流速度对壁面的冷却程度不一样。取冷却水充分流通后的壁面温度研究入口水流速度对壁面温度的影响。

由图18可以看出，当入口水流速度为2m/s时，冷却效果最好，其壁面最小温度可以达到680K(407℃)左右。随着入口冷却水的速度减小，冷却效果降低，但幅度不大。当入口水流速度为0.4m/s时，壁面的最低温度为695K(422℃)，相比入口水流速度为2m/s时温度仅上升15K。

2.3.4 综合性能比较

从传热角度来说，入口速度越大，冷却水带走的热量越多，但分析发现，当冷却水速度由2m/s降低到0.4m/s时，壁面最低温度仅略微提高。从压强角度来看，当冷却水入口速度由0.4m/s提高到2m/s时，压强提高了数十倍。空气舵使用过程中，为了避免产生回流后，出口水又将以汗蒸形式流出的情况，因此综合考虑入口水流速度对空气舵表面温度以及出口压强的影响，应选择较低速度，此时空气舵出口压强较小，而且表面温度变化不大。

3 结论

本文结合LPBF工艺设计了结构功能一体化的复杂点阵结构空气舵模型，并通过实验研究确定了适用于TC4材料成形可获得较高相对致密度的V=55J/mm3～62.5J/mm3的较优工艺区间，并进行了空气舵(部分)的打印，验证了优化工艺参数的可行性。并基于有限差分法，建立了点阵结构空气舵的CFD流固耦合共轭传热的计算模型，利用VOF方法追踪流体自由液面，计算过程中考虑了水和钛合金材料的热物性参数随温度的非线性变化行为及湍流换热特性，采用顺序耦合热结构进行热分析，考虑了计算的效率及准确性采用局部分析的方法，分析了冷却水的入口速度分别为0.4m/s、0.8m/s、1m/s、2m/s时，空气舵内部的流体速度、压强计空气舵壁面的分布情况。研究表明，空气舵的内部流体压强随速度的增加剧烈增加，从而导致流体出口的速度增加。当压强增加到一定程度时，流体的出口以水柱形式喷出。综合空气舵的使用要求，即达到降温的要求，又满足空气舵的出口水以汗蒸形式流出的情况，冷却水的入口速度采用0.4m/s～0.6m/s为最佳。