飞行器气动参数智能在线辨识技术研究

浦甲伦，韩业鹏，张 亮

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

对于大气层内长时间飞行的飞行器，如巡航导弹、滑翔导弹，空气动力是影响最大也是最复杂的外力[1]。在实际飞行中，如果气动参数变化剧烈，在地面基于标称气动设计的轨迹及控制系统可能无法满足实际需求，此时通过在线气动参数辨识可规划更准确的飞行轨迹，对控制参数进行自适应调整，从而适应气动参数变化的情况。因此,针对导弹飞行中的在线快速、精确辨识技术进行研究显得极为迫切[2]。

导弹气动参数辨识是指利用导弹在试验或实际飞行中测得的输入和输出数据，采用系统辨识技术，建立反映导弹本质动态特性的气动力数学模型，并辨识出数学模型中的待定系数[3]。气动参数辨识核心3要素是：模型、数据和等价准则。从是否依靠模型的角度可将系统辨识的方法分为两大类：一类是基于模型的参数辨识，即首先建立系统的状态方程和观测方程，利用参数辨识方法对模型的参数进行辨识；另一类是部分依靠模型或完全不依靠系统模型的辨识方法，利用给出的输入和输出数据，同步辨识出系统模型和模型参数[4]。

一般来说，导弹气动参数辨识通常是基于模型的参数辨识：首先根据导弹特性和力学基本规律，采用推理方法，建立系统动力学方程组——状态方程组。然后利用系统试验或系统运行中测得的输入和输出数据，辨识出动力学方程组中的气动因素，包括建立气动力数学模型，并辨识出气动力数学模型的待定参数[5]。此类基于模型的常规辨识方法适用于离线气动参数辨识问题，包括基于气动数据插值表的气动系数、气动导数及配平舵偏角参数化模型的离线辨识技术，以及基于历史飞行试验数据的气动系数、气动导数、配平舵偏角模型的修正技术。所涉及的算法包括极大似然法、最小二乘方法和如粒子群优化、混合遗传算法等智能优化算法[6]。

对于大多数导弹动力学系统，理论建模工作比较成熟，有现成完整的动力学方程组，且气动力数学模型有工程应用较为简便而合理的形式。故而，导弹气动参数辨识变成了利用飞行或地面试验的实测数据，估计气动力数学模型中未知参数的问题。参数估计的任务是根据试验测得的样本推断未知参数的数值，因此导弹气动参数辨识问题主要解决参数估计准则和估计算法两个问题[7]。

通常来说，不依靠系统模型的参数辨识相对基于系统模型的参数辨识来说，在算法效率、辨识精度上都处于劣势，随着人工智能特别是神经网络的发展，通过机器学习的方式得到逼近真实系统模型的训练模型的辨识方法，获得了新一轮关注，在诸如气动参数辨识、电机参数辨识、惯性器件参数辨识等方面成为了新的研究方向[8]。目前，神经网络在气动参数辨识方面已获得较为广泛的研究和应用，如PNN(感知器神经网络)、BP(反向传播)神经网络、Hopfield网络等，以及近年来获得关注的基于多层神经网络的深度学习网络，如RBM(限制玻尔兹曼机)、CNN(卷积网络)、DBN(深度置信网络)等[9-11]。

本文将以神经网络(Neural Networks，NN) 为基础，研究单隐层和多隐层神经网络在气动参数辨识问题中的应用,并针对在线气动参数辨识的需求，结合支撑向量机(Support Vector Machine，SVM)方法与神经网络技术，设计可行的在线气动参数辨识方案。

1 气动参数智能辨识流程设计

当导弹飞行时，纵横向运动相互耦合，必须采用六自由度运动方程作为导弹动力学系统的数学模型，其中气动参数是未知的。首先给定气动参数的一组初估值，计算六自由度运动方程对输入测量值的响应，并与真实系统输出的测量值进行比较，判断是否满足一定的等价准则，如果不满足，则修正气动参数。反复这一过程，直至满足等价准则为止，从而得到正确的气动参数。

智能气动参数辨识方法主要是基于神经网络方法和SVM方法。SVM可以用于对其他方法建立的模型的参数进行训练，如图1所示。SVM可以对神经网络的参数或六自由度模型的参数，以及其他一些算法的参数进行学习。SVM可直接利用输入输出数据进行训练，给出训练后的模型，同时给出关注的参数，也可以对经其他方法处理后的样本进行学习。SVM还可用于子样的扩充，即利用已有的小样本数据作为SVM的原始训练样本，寻找SVM的最优参数，继而用训练后的模型对小样本数据进行预测扩充。并且，针对在线参数辨识问题，可以将SVM方法与神经网络结合使用。即利用SVM的快速和少数支撑向量决定结果的特点，设计模型修订策略，在线对已经离线训练好的神经网络模型进行修订。

图1 结合SVM的气动参数智能辨识Fig.1 Intelligent parameters identification with SVM

传统的气动参数辨识需要解决的是参数估计准则和估计算法问题，而智能参数辨识主要解决的是神经网络的网络模型、输入输出数据和网络训练问题。

2 导弹气动参数智能在线辨识方案设计

在对导弹气动参数进行在线辨识时，应着重考虑快速性和准确性，并考虑一定的自适应性。其基本的辨识模型和辨识方法与离线工况类似，不同之处在于要结合离线辨识的结果，针对在线辨识的时间、计算量等较为严苛的约束条件，设计合理的辨识流程和方案。

在对离线参数辨识研究的基础上，还需针对性地对模型简化和快速辨识方法及方案、流程设计进行深入研究。

2.1 气动参数辨识模型的简化

可按如下两种思路对气动参数辨识的模型进行简化：一是通过参数分析，减少待辨识参数数量，降低辨识模型维度；二是结合特定辨识方法，将基本模型拆解为多个简单的、低维的待辨识模型。

假定气动参数辨识基本模型(具体的模型将以基本模型为基础，根据导弹的特点进行一定的修正，然后可根据实际需求选择状态变量和观测变量，建立相应的状态方程和观测方程)如下：

(1)

2.2 在线快速辨识算法

通过滤波的方法可以把改变参数估计问题转化为状态估计问题，依据飞行器系统实际情况，采用连续估计模型，并通过离散时间测量和离散滤波算法达到实时效果。针对一般问题，扩展卡尔曼滤波、无迹卡尔曼滤波、自校正滤波等算法均能保持良好的滤波质量和收敛速度。其中，自校正滤波采用的现代时间序列分析方法是最优滤波的新方法论。基本工具为向量自回归滑动平均模型(Autoregressive Moving Average，ARMA)， 因其在快速参数估计上的口碑，本文采用ARMA模型来提高在线估计速度。

现代时间序列分析方法的理论基础是白噪声估计理论，利用该理论可以解决状态和信号估计问题的机理是：由状态空间模型或传递函数模型，可将系统状态和信号表为输入白噪声、观测白噪声和观测信号三者的线性组合，因而可将状态和信号估计问题转化为白噪声估计和观测信号预报问题，即状态空间模型可按规则转化为ARMA模型，二者是等价的。用ARMA的递推辨识器伴随最优滤波器得到自校正滤波器。采用某种辨识方法估计ARMA模型参数，用其代替真实值代入最优滤波器，得到相应的次优滤波器。如参数估值收敛，则此次优滤波器渐进于相应的最优滤波器。

(1)ARMA模型

设系统的随机输入e(t)∈Rm为m维白噪声Ee(t)=0，E[e(t)Te(j)]=Qeδtj，其中δtj=1(t=j)，δtj=0(t≠j)，且输出y(t)∈Rm，有模型y(t)∈Rm

y(t)+A1y(t-1)+…+Anay(t-na)=
C0e(t)+C1e(t-1)+…+Cnce(t-na)

(2)

其中Ai、Ci为m×m系数阵，na、nc为模型阶次。

引入q-1为滞后算子，满足

q-1x(t)=x(t-1)

(3)

并引入多项式矩阵

A(q-1)=Im+A1q-1+…+Anaq-na

(4)

C(q-1)=C0+C1q-1+…+Cncq-nc

(5)

则ARMA模型可表示为

A(q-1)y(t)=C(q-1)e(t)

(6)

在不引起混淆的情形下，可省略q-1，记为

Ay(t)=Ce(t)

(7)

(2)状态空间模型与ARMA模型的转化

状态空间模型与ARMA模型可以相互转化。通过如下转化过程，可将参数辨识的基本状态空间模型转化为ARMA模型，之后可利用估计方法求解。

为了表述方便，首先将状态空间模型写为：

x(t+1)=Φx(t)+Γw(t)

(8)

y(t+1)=Hx(t)+ν(t)

(9)

引入无关测噪声信号s(t)=Hx(t)，则有

s(t)=H(In-q-1Φ)-1q-1w(t)

(10)

利用矩阵求逆公式有如下ARMA模型

det(In-q-1Φ)s(t)=Ηadj(In-q-1Φ)-1Γq-1w(t)

(11)

y(t)=s(t)+ν(t)

(12)

现代时间序列分析方法的基本工具是ARMA新息模型，而Kalman滤波的基本工具是Riccati方程的求解。比较构造ARMA新息模型和Riccati方程求解的计算量，可以得出结论：在Kalman滤波方法中，用迭代法求解Riccati方程，要求进行m×m矩阵求逆和n×n矩阵的乘法运算；而现代时间序列分析方法中，用Gevers-Wbuters迭代算法构造ARMA新息模型要求m×m矩阵求逆和m×m矩阵的乘法运算。因此当n>m时，通常构造ARMA模型的计算量要比求解Riccati方程小。

2.3 在线快速辨识方案设计

在上述参数辨识方法的研究基础上，可设计采用神经网络方法结合SVM方法的在线辨识方案：

1)利用神经网络进行离线学习，训练和校核神经网络模型(或系统动力学模型)的参数，然后在此基础上简化(考虑参数灵敏度、参数重要程度、参数影响程度)和设计(结合SVM)在线辨识模型。

2)在线辨识时不再对模型进行复杂训练，可采用固定参数、参数切换和利用SVM在线快速修正几种不同方式，避免在线进行大量计算且能够有效节省存储空间。其中，将重点研究结合SVM的神经网络在线快速修正技术，即利用SVM的特点，在新的数据处于分类间隔外时，不对辨识模型进行修正；反之，通过更新支撑向量的方式快速修正模型。

3)对模型的描述(包括离线模型建立及其训练阶段)采用现代时间序列分析方法，以进一步满足在线要求，在线计算过程中的优化方法也将采用递推最小二乘、混合蛙跳等计算量较小的方法。

最终采用的在线智能快速气动参数辨识方案如图2所示。

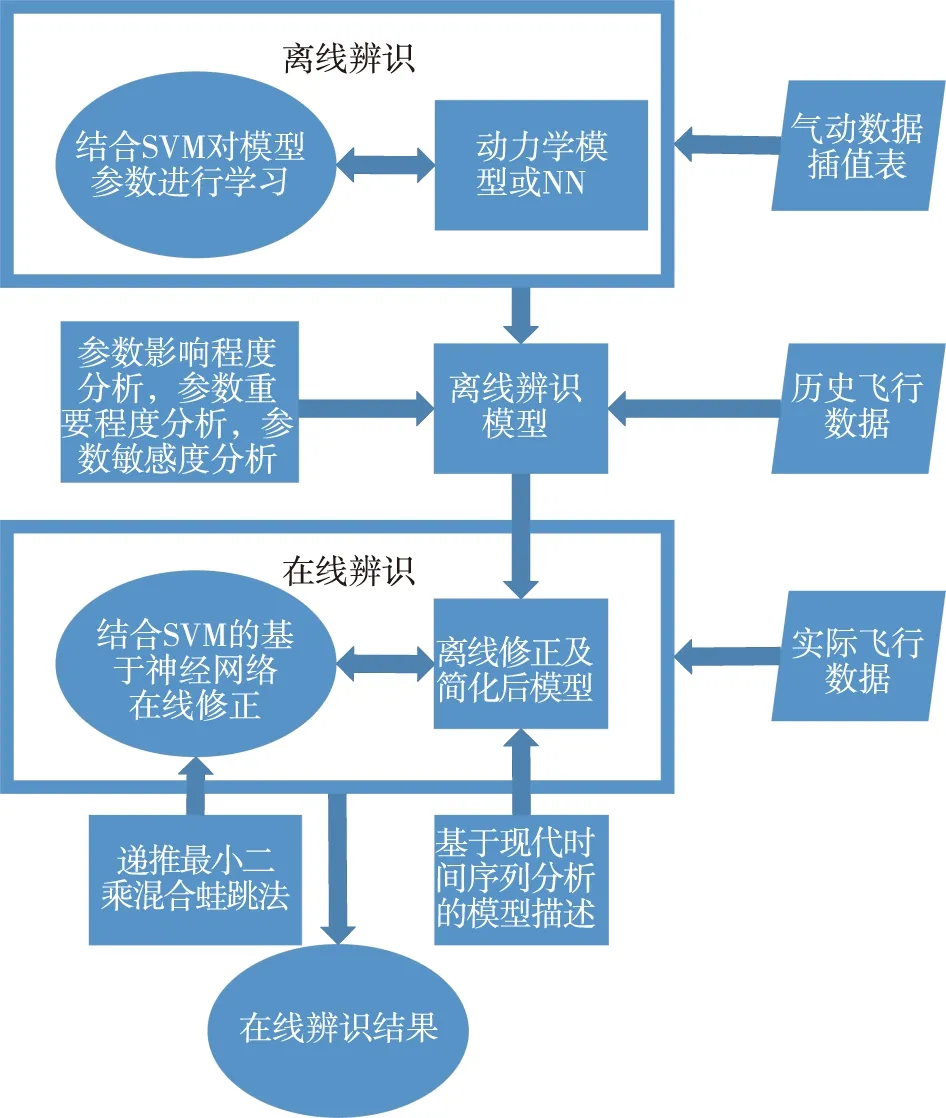
图2 导弹气动参数在线快速辨识方案Fig.2 Project of online missile aerodynamic parameters identification

3 基于小波神经网络的气动参数辨识

本文首先采用神经网络中的小波网络(Wavelet Neural Network, WNN)建模方法进行气动参数辨识方法研究。

3.1 小波神经网络的构建

小波建模首先根据样本数据的时频特性，初步确定出可用的小波基函数及其数目L，然后根据预测误差最小的思想将样本数据分成两部分，进一步按输出均方误差准则确定出模型的最优小波基数目S，同时进行优选确定相应的小波基函数集，最后，选择参数调整训练算法确定小波网络权值。

小波网络结构设计中包括隐层节点数确定和节点激励函数选取两个方面。在实际应用中，一般选取具有单隐层的3层神经网络结构。单隐层前向神经网络对非线性函数的逼近研究得最早，且理论上早已证明单隐层神经网络能以任意精度逼近连续函数。

常用的激活函数有δ(x)=1/1+e-x，δ(x)=(ex-e-x)/(ex+e-x)等。小波网络与一般前向神经网络不同之处在于隐层神经元的激活函数为小波函数，并且每个激活函数的参数都不同。

本文选用连续参数小波网络，即小波参数(aj,bj)是连续变化的，单输入单输出网络模型可表示为：

(13)

wj为输出变量与第j个小波基之间的连接权值，aj和bj分别为小波基的伸缩和平移参数，S为小波基的个数。上面结构中加入了线性项cx+d,它反映系统的线性特性，这在实际应用中是非常有意义的，因为实际系统是线性和非线性的统一，一定条件下可表现出明显的线性特性，特别是对于导弹气动系数的建模，系数同时具有线性和非线性特性，加入一些具有明确物理意义的线性项是适当的，这既能扩展模型的适用范围，又能提高建模精度。

对于多输入多输出(MIMO)系统建模，可以得到类似的结构形式。因为气动力系数模型属于多输入多输出系统，所以下文主要针对MIMO系统的建模展开论述。

设p维输入向量为X,X∈Rn,q维输出向量为Y,小波网络的隐层节点数量随输入维数p呈指数级增长。假设单输入时隐层节点数为n，在p维输入情况下采用小波基标量积的方式构造网络结构，即用式(14)构造多维小波网络隐节点函数。

ψ(x1,x2,…,xp)=ψ(x1)ψ(x2)…ψ(xp)

(14)

则所需隐层节点数就变为np，随着输入维数的增加，隐层节点数将达到很高的数量级，这就是小波网络的所谓“维数灾(curse of dimensionality)”问题。

输入和输出的关系式可表示如下：

(15)

Y=W×ψ+CX+D

(16)

其中权值和参数矩阵表达式为：

(17)

3.2 小波神经网络的训练

训练采用基于最小二乘的递推正交最小二乘法(ROLS算法)。正交最小二乘算法虽然避免了求逆矩阵，但当N很大时，QR分解计算量非常大，难于实现在线计算。因此，本小节将采用ROLS算法来实现QR分解。

(18)

(19)

J(W(n))取极小值的线性输出权矩阵W(n)和n组样本输入时网络输出与期望输出的偏差分别计算如下：

(20)

(21)

ROLS训练的算法程序如下：

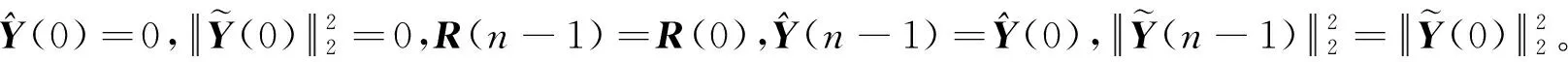
可以看到，ROLS算法解决了矩阵H为病态的问题；W为唯一确定且误差平方和最小；不需要计算中间步骤的W(n)；每增加一组新数据，做L次变换，计算量小，可用于参数的在线辨识。

4 结合SVM方法的气动参数辨识

在气动参数辨识中，可将多个参数的辨识问题处理为测量值与预测值之间误差的正负分类，然后利用诸如最小二乘、极大似然、智能算法等方法进行参数估计。也可按一对其余的或一对一办法转化为多个二分类问题，再求解对应的回归问题。

4.1 SVM对回归问题的求解

SVM用于回归问题的基本思想是：根据观测数据y=[y1,y2,…,yl]T估计未知函数f(x,w)的参数w=[w1,w2,…,wl]T，即

y=f(x,w)+b

(22)

式中，b表示观测值与预测值间的误差，x表示特征变量，与对应的观测数据y组成训练数据集合，{(x1,y1),(x2,y2),…,(xl,yl)}。

未知函数项f(x,w)可表示为：

(23)

式中，Φ(·)为将训练数据从输入空间映射到希尔伯特(Hilbert)空间的函数。

针对气动参数辨识问题，y=[y1,y2,…,yl]T为观测数据，x对应于待辨识的参数(气动系数、气动系数导数或模型的参数)，f(x,w)为未知的，用于描述待辨识参数和观测数据之间关系的函数。

用于回归问题的SVM又称支撑向量回归机(Support Vector Regression, SVR)，其模型可表示为：

(24)

式中，ε表示SVR预测值与实际值之间的最大误差。在ε合适的情况下，式(24)可得可行解。二维平面下的几何意义是所有训练点都应该在回归直线的ε之内。

在实际应用中，存在干扰、误差等各种因素，通常不能够求出可行解。因此，引入ξ、ξ*容许少量实例的训练误差落到ε外：

(25)

其中，每个训练实例都有对应的ξ、ξ*，用于确定该实例的训练误差是否落在ε之外，惩罚系数C用于调节训练模型，避免模型过拟合或欠拟合。

式(25)是定义在Hilbert空间上的凸二次规划问题，难以直接求解。引入拉格朗日乘子a、a*、β、β*，得到拉格朗日方程：

(26)

当拉格朗日函数对个变量的1阶偏导数等于0时，原问题的目标函数取最小值，即：

(27)

可得到回归估计函数的参数：

(28)

同时得到了原优化问题的对偶问题：

(29)

(30)

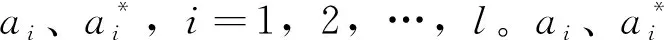
从而有未知函数可写为：

(31)

为了便于计算，通常将Φ(xi)TΦ(x)用核函数代替，即：

K(xi,x)=〈Φ(xi)TΦ(x)〉

(32)

于是有

(33)

(34)

(35)

从而得到回归估计函数为：

(36)

在诸多核函数中，采用径向基核函数(Radial Biasis Kernel Function，RBF)的SVM对非线性系统有较好的逼近能力。所以在对非线性系统进行黑箱辨识时，选取RBF核函数的精度比较高，而对于线性系统进行参数辨识时，多采用线性核函数。

4.2 基于SVM的小子样修正问题

气动参数辨识中往往会面临样本数不充足的问题，此时可采用基于SVM的小样本修正。利用已有的小样本数据作为SVM的原始训练样本，采用网格搜索法寻找SVM的最优参数，继而用训练后的模型对小样本数据进行预测扩充，最后利用扩充的样本进行可靠性参数估计。方法利用了SVM在处理小样本回归问题上的优势，无需先验知识，有效改善了最小二乘参数估计对样本容量非常敏感的问题。

5 飞行器在线参数辨识仿真结果对比

仿真工况设置如下：

1)飞行器为再入飞行器，保持纵平面内飞行；

2)飞行器外形为轴对称，横截面为半椭圆形；

3)仿真中所用飞行器气动数据以CFD软件仿真结果为“真实值”，离线训练数据用“真实值”+单向20%均值随机偏差获得；历史飞行数据用“真实值”+10%单向随机偏差生成；实际飞行数据分为两组，第一组与历史飞行数据生成方法一致，第二组在“真实值”基础上附加单向5%随机偏差，用于考核在线修正性能。上述偏差均为正态分布。

4)离线样本数每次仿真使用10000组；历史飞行数据样本数每次仿真使用10～100组；实际飞行数据每次使用1组。

5)本文重点分析各辨识算法，尤其是智能方法在在线气动参数辨识的可用情况，因此，将气动力和气动力矩模型简化至1阶。

6)用于对比的辨识方法包括：传统的最小二乘准则及最小二乘优化、传统极大似然准则及优化方法、极大似然准则加粒子群优化、单层小波神经网络、结合SVM方法可在线调整参数的神经网络、利用SVM扩充样本的神经网络。

经过1000次仿真后，分别对0阶气动力、0阶气动力矩、1阶气动力、1阶气动力矩参数的辨识结果进行统计，求取相对于“真实值”的误差均值，最终得到的对比结果如表1～表4所示。

表1 0阶气动力参数辨识对比(3σ)

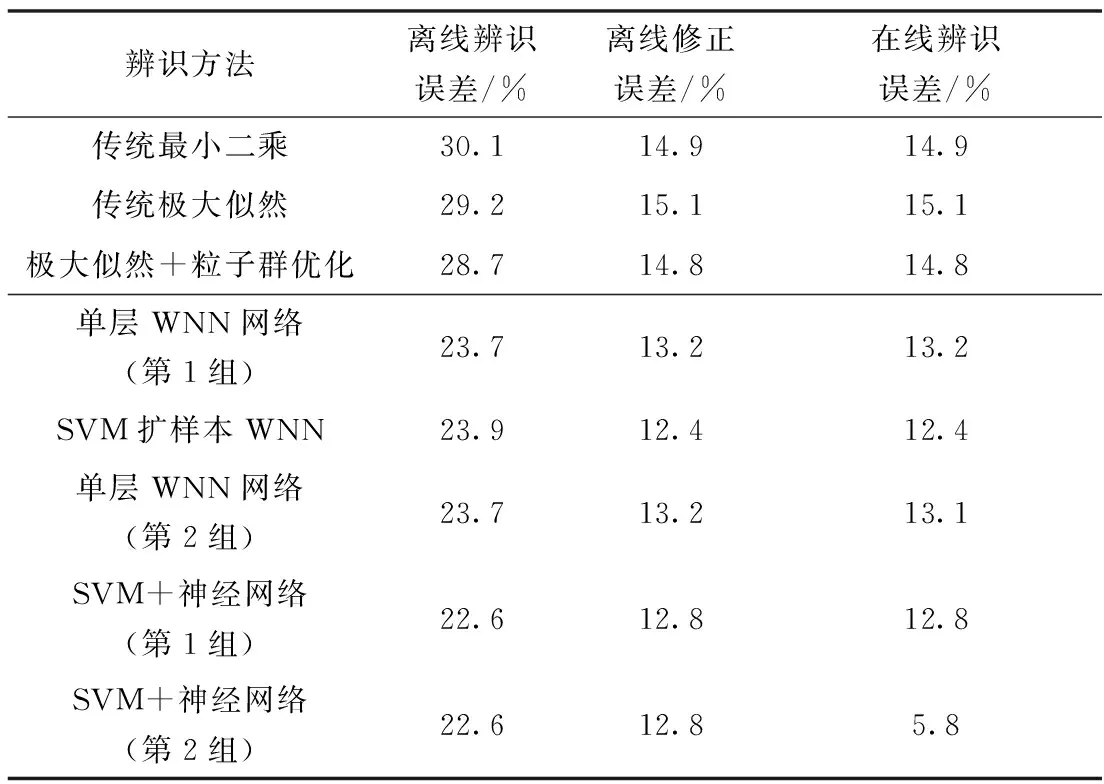
表2 0阶气动力矩参数辨识对比(3σ)

表3 1阶气动力参数辨识对比(3σ)

表4 1阶气动力矩参数辨识对比(3σ)

可以看到，利用神经网络的智能参数辨识方法与“真实值”相比的辨识精度上比传统方法有3%～10%的提高。并且，辨识结果相对真实值的误差与生成离线训练数据相对“真实值”增加的偏差均值(20%)更为接近，说明利用神经网络能够更好地拟合复杂的气动模型。

表5中的数据是在相同的配置和仿真试验条件下获得的，其中离线训练采用10000组数据、离线修正采用100组数据。在线辨识速度给出的是连续运行1000组仿真的平均时耗。

表5 气动参数辨识效率对比

可以看到，虽然利用神经网络的智能方法需要较长的训练时间，但其在线运算速度耗时很少。建模时采用ARMA模型的现代时间序列分析能够稍微提高传统辨识的速度，但相对于不需要在线训练或采用简化在线调整的智能辨识方法，辨识速度的提升很有限。

6 结论

本文研究了基于智能方法的飞行器气动参数在线快速辨识问题。首先给出了基于智能方法参数辨识的辨识流程，然后在此基础上，从简化模型、提升算法效率、设计合理辨识流程3方面出发设计了气动参数智能在线辨识方案。然后，本文给出了基于小波神经网络的气动参数辨识模型，并结合辨识流程和方案，将SVM方法引入智能气动参数辨识过程中。最后，在给定的假设条件和仿真工况下，进行了大量的仿真并对结果进行了统计。结果表明，本文提出的气动参数智能在线快速辨识方案辨识精度比传统方法提高了3%～10%，且对训练数据的拟合精度更高；同等条件下，智能在线快速辨识的时耗仅为传统方法的1/10左右,说明本文提出的智能气动参数在线快速辨识方案具有较高的应用价值。