基于ANFIS的智能导航自适应滤波算法研究

吴 鹏，穆荣军，邓雁鹏，孙绪尧

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

智能导航是飞行器信息化系统的信息基础，而具备智能化推理、决策等功能的自适应滤波算法是智能导航系统设计的核心环节。在传统的导航数据融合滤波器设计中，滤波器的各项参数往往是通过多次离线评估优化得到的，而对于诸如智能变形导弹等智能飞行器，一般具有复杂动力学特性，离线优化的参数往往不能满足智能导航滤波器精度的需求。采用人工神经网络技术辅助智能导航滤波器有两条途径：1)对状态估计滤波器的内部参数进行实时监测和调整，达到优化滤波的目的；2)直接对状态向量解算误差进行补偿。在实际应用中，由于使用场景不同、建模所需的必要条件无法准确获得等原因，状态向量解算误差无法直接测得和补偿，此时可以通过引入模糊推理、专家系统、人工神经网络等智能化方法对载体工况进行识别和评估，实时修改滤波器内部参数来修正偏差。

建立对象模型是控制系统设计的基础，以智能导弹的快速跨域飞行为例，由于其具有工作环境多变、机动特征复杂、飞行参数包线大等特点，传统的数学工具难以对其工作中产生的有色噪声和随机噪声进行精确的模型构建，而ANFIS自适应网络模糊推理技术可以对这些噪声进行实时预测并补偿[1]。

1 基于ANFIS改进的自适应滤波器设计

1.1 ANFIS构建

ANFIS是一种将模糊逻辑和人工神经网络结合起来的技术，它不需要系统或系统误差的精确模型，而是仿照人类推理和决策过程构建If-Then规则库，以此确定隶属度函数和模糊控制系统，同时采用误差反向传播和最小二乘法对修正模型中的前提参数和结论参数实现模糊推理功能，进而实时修改滤波器内部参数，补偿由于环境变化、工况改变等因素带来的误差，达到优化状态估计滤波器的目的。

常见的T-S型ANFIS系统通常使用如下规则：

ifxisAandyisB, thenz=f(x,y)

(1)

式中，A和B是前提的模糊数，z=f(x,y) 为结论中的精确数。

ANFIS系统结构常用的Sugeno模糊模型如图 1所示[2]，它为具有两个规则的1阶T-S性ANFIS结构模型，规则如下：

ifxisA1andyisB1, thenf1=p1x+q1y+r1

ifxisA2andyisB2, thenf2=p2x+q2y+r2

(2)

图1 ANFIS结构图
Fig.1 ANFIS structure diagram

模型各层的具体定义和功能如下：

第1层：本层为前提参数,负责摄入信号的模糊化。该层的每一个节点i都是一个具有节点函数的自适应节点，假设节点i的输入量为x(或y)，与该节点有关的语言标识为A(或B)。该节点函数同时也是模糊集A(或B)的隶属函数，其决定了所给定的x(或y)满足A(或B)的程度。节点i具有输出函数：

(3)

(4)

式中，ai、bi、ci为前提参数，隶属度函数的形状随着这些参数的改变而改变。

第2层：该层为固定节点，输出所有输入信号的积，每个节点的输出表示某一条规则的可信度：

wi=μAi(x)×μBi(y)

(5)

第3层：该层计算每条规则的归一化可信度为：

(6)

第4层：该层为结论参数层，该层节点为具有节点函数的自适应节点，用来计算每条规则输出对最终结果的影响，输出为：

(7)

式中，pi、qi、ri为结论参数。

第5层：该层为所有节点总输出：

(8)

给定前提参数后，ANFIS输出可以表示成结论参数的线性组合：

(9)

1.2 基于ANFIS优化的自适应滤波算法设计

应用ANFIS进行改良Kalman滤波时，需要使用大量先验数据对神经网络进行训练，先根据数据特性对数据进行模糊分类，然后让ANFIS对分类规则进行学习[3]。T-S型ANFIS模糊结构比常规模糊模型有更强的表达能力。但是T-S型模糊结构对输入变量进行的是线性分类，当输入变量维数很大或为非线性变换时，为保证输入变量彼此独立，输入空间通常会被分割得很细，使If-Then规则库中模糊规则数目迅速增加，模糊推理系统变得复杂，计算量增大，计算效率降低。为使ANFIS系统对输入空间进行非线性划分，减小系统复杂度，可以引入减法聚类(Subtractive-Clustering)解决此问题。对于智能变形导弹快速跨域飞行等工作情况，由于难以对导航数据类别进行初始划分，减法聚类算法可以根据输入数据的密度特征自动形成一个具有最少规则数目的模糊推理规则库。首先计算输入空间内每个点影响半径内数据点的密度，将具有最高数据点密度的中心点作为第一个聚类中心，同时把其影响半径内的其他点从数据空间中删除，在剩余点中按照这种选取规则再次筛选聚类中心点，直到影响半径内点密度低于预先设置的阈值[4]。

在Kalman滤波工作时，随着工作时间增加，测量传感器的可靠性会发生变化，在大多数情况下，量测数据可靠性会下降，但是在个别情况下，量测可靠性会增加，体现在Kalman滤波模型中就是量测噪声误差方差会随着滤波发生变化。因此，在以惯性导航INS为核心的组合导航系统中，利用ANFIS自适应神经网络结构推理系统可以对当前使用场景进行推理，以滤波器中的新息为观测对象，将新息序列方差与理论方差进行对比，实时判别由于环境等因素对滤波系统带来的影响，以此为依据实时修正量测噪声误差方差，优化Kalman滤波系统。

新息序列方差计算公式和理论方差计算公式分别为：

(10)

(11)

由式(11)可以看出，Rk和Sk成正比关系，据此可以定义模糊调整规则为：

if dmk(i,i)=0，thenRk(i,i) 不变；

if dmk(i,i)>0，thenRk(i,i) 减小；

if dmk(i,i)<0，thenRk(i,i) 增大。

定义失配度(degree of missmatching)变量dm：

(12)

ANFIS神经网络辅助组合导航滤波器设计结构如图2所示。

图2 ANFIS优化滤波算法结构Fig.2 Improved Kalman Filter structure diagram based on ANFIS

Rk的维数为N，采用对应N个ANFIS网络对Rk对角线上每一维的数值进行调整。

定义失配度增量Δdm：

Δdmk=dmk-dmk-1

(13)

每个ANFIS网络的输入均为dmk(i,i)和Δdmk(i,i)。采用ANFIS网络的输出ΔRk(i,i)对Rk进行调节：

Rk=Rk-1+ΔRk

(14)

通过上述算法对Kalman滤波进行优化，可得到更准确的结果。

2 基于ANFIS优化的自适应滤波算法仿真

在实际导航应用中，随着工作时间变长，载体量测传感器的可靠性会发生变化，如采用视觉传感器时，随着使用时长增加，传感器噪点会变多，测量精度会降低。基于这种假设，可以使用ANFIS控制器对使用场景进行学习，根据学习结果对Kalman滤波进行补偿，进而改善滤波结果。

基于ANFIS学习的滤波修正算法仿真由以下步骤组成：

1)ANFIS训练数据获取；

2)训练自适应网络模糊推理模块；

3)利用训练好的自适应网络模糊推理模块修正Kalman滤波。

考虑到本仿真实验目的是为了验证ANFIS对Kalman滤波具有修正作用，旨在抑制变形导弹运动过程中的非Gauss噪声。仿真中主要对量测噪声方差R进行调整，验证方法对非Gauss噪声的抑制作用。在这个层面上，优化是否有效与系统复杂度没有关系，只与失配量dm是否被抑制有关。对受影响的特定通道进行分析即可说明问题，且加入ANFIS模块后，运算量较大，故选取一个简化后的空间运动7维模型进行Kalman滤波设计，7维状态向量为：

X=[φxφyφzδVxδVyxy]

(15)

P0= diag [(1°)2(1°)2(1°)2(0.1m/s)2

(0.1m/s)2(1000) (1000)]

Q=diag [(0.01°/h)2(0.01°/h)2(0.01°/h)2

(10μg)2(10μg)2(0)(0)]

Ri=diag [(ri)2(ri)2(ri)2(10-4)2(10-4)2(10-2) (10-2)]

其中，Ri为预设的量测误差方差，设置成一个变化规律为N(1-e-t,0.0015×t)的变量，形成非Gauss噪声，只对系统姿态角产生影响。

未加入ANFIS模块时，滤波得来的数据作为ANFIS训练数据，姿态角滤波估计结果如图 3所示。图3(a)、(c)、(e)分别为未经修正的姿态角估计结果,图3(b)、(d)、(f)分别为对应姿态角误差，将以上数据作为ANFIS训练数据。

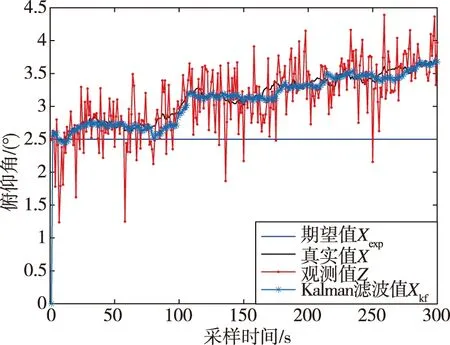
(a)未经修正的俯仰角估计结果

(b)未经修正的俯仰角滤波误差

(c)未经修正的偏航角估计结果

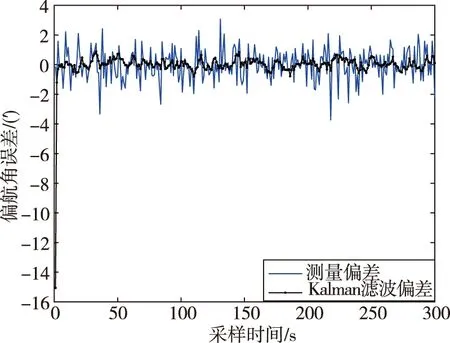
(d)未经修正的偏航角滤波误差

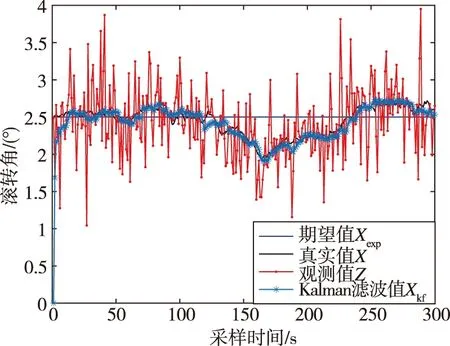
(e)未经修正的滚转角估计结果

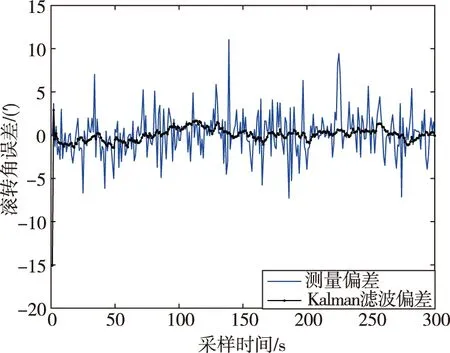
(f)未经修正的滚转角滤波误差

由于量测误差方差变化，引起的姿态角失配度如图 4所示。

(a)未经修正的俯仰角失配度

(b)未经修正的偏航角失配度

(c)未经修正的滚转角失配度图4 未经修正的失配度Fig.4 Degree of miss-matching without ANFIS

获得训练数据之后，利用训练数据解算失配度dm及失配度增量Δdmk，以失配度dm、失配度增量Δdmk为输入，量测误差方差变化量ΔR为输出，构建训练矩阵，首先使用subtractive聚类算法对300组数据进行分类，然后根据分类得到的分类规则，对ANFIS模块进行训练，形成模糊推理规则，对Rk进行调节。

经过修正的Kalman滤波结果如图5所示。图5(a)、(c)、(e)分别为经过修正的姿态角估计结果，图5(b)、(d)、(f)分别为对应姿态角误差。

由于量测误差方差变化引起的姿态角失配度如图 6所示。

(a)修正的俯仰角估计结果

(b)修正的俯仰角滤波误差

(c)修正的偏航角估计结果

(d)修正的偏航角滤波误差

(e)修正的滚转角估计结果

(f)修正的滚转角滤波误差

(a)修正的俯仰角失配度

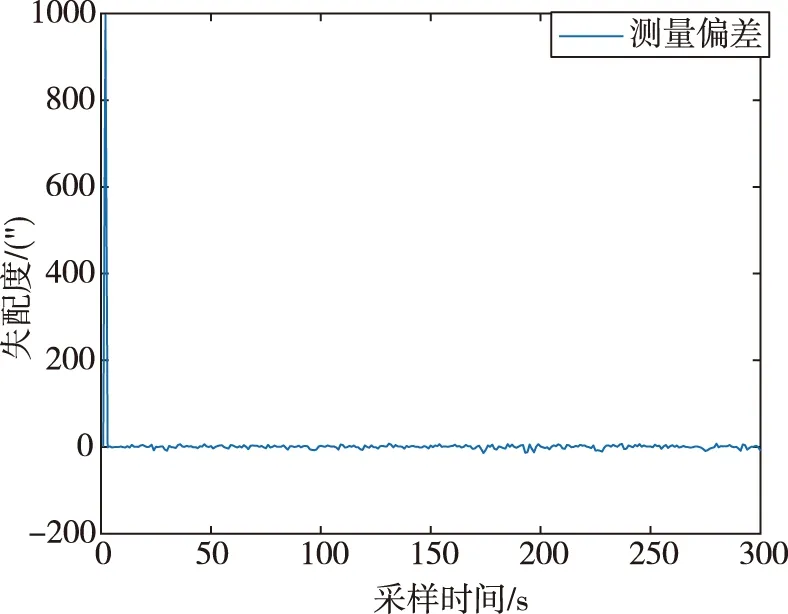
(b)修正的偏航角失配度

(c)修正的滚转角失配度图6 修正的失配度Fig.6 Degree of miss-matching with ANFIS

由以上仿真结果可知，在工作环境已知或在外部环境对导航传感器影响已知情况下，基于ANFIS修正的Kalman滤波对变化的环境具有较强的适应性作用，滤波性能有了较明显的提升。以俯仰通道为例，在ANFIS校正前，经过300步Kalman滤波，状态向量中滚转角估计均方误差约为10.382，后100步滤波的失配度均值约为5.8993；经过ANFIS修正后，估计均方误差下降至约为4.941，后100步滤波平均失配度下降到3.3173。由此可以看出，相对于标准Kalman滤波结果，ANFIS控制器对量测噪声起到了较好的抑制作用，降低了估计误差，提高了导航精度。

为使研究结论更加可信，在相同参数下对本模型进行1000次重新训练并进行Monte Carlo打靶，统计结果如图 7所示。仿真结果表明，基于ANFIS修正后的自适应非线性Kalman滤波方法适应性更好、精度更高。

3 结论

本文首先分析了ANFIS的结构和模型，对将ANFIS技术与传统Kalman滤波相结合的方法进行了研究；然后结合ANFIS减法(Subtractive)聚类方法，提出了一种基于ANFIS优化的智能导航自适应滤波算法；最后采用该算法对仿真工况进行组合导航滤波仿真验证，通过1000次Monte Carlo打靶试验进行数据统计学分析。仿真结果表明，ANFIS系统在具有可行的充分训练数据支持下，可有效实现对Kalman滤波器的改进，自适应补偿参数误差，获得更好的滤波结果；其模糊推理和聚类过程，体现了自主学习、智能决策等特点，对于构建智能导航系统作用明显；优化的滤波算法依赖环境模型或者环境对飞行器导航系统的影响模型，在不同工作环境下需要对ANFIS模型重新训练。

图7 ANFIS修正滤波结果分布统计直方图Fig.7 ANFIS corrected distribution histogram of Kalman Filter