几个关于极坐标的Bonnesen型不等式

郑高峰,周 阳

(华中师范大学数学与统计学学院,湖北武汉 430079)

1 引言

经典等周不等式:对平面内任一条简单闭曲线γ,设其周长为L,所围区域面积为A,有

等号成立当且仅当γ是一个圆周.

1882年,Edler第一个给出严格的数学证明,此后相继出现多种不同证明方法[3],而在这些证明中,用到极坐标的情况非常少,不等式中带有极坐标形式的基本没有.因此给出一些带有极坐标形式的等周型不等式是必要的.并且从文中定理2.4,定理2.5中带有极坐标的等周型不等式来看,当L2−4πA=0时,可以很直观的发现该曲线为圆周.

2 主要结果及其证明

引理2.1[4]对任意一条简单闭曲线γ,存在唯一一个包含γ的最小圆环.并且至少存在四点P1,P2,P3,P4,其中P1,P3在该圆环的内圆周上,P2,P4在该圆环的外圆周上,使得P1,P2,P3,P4依次排列在曲线γ上.

注 Chouikha[5]对Jordan多项式的情形作出了证明,在文献[4]中推广到一般简单闭曲线.

接下来,如无特别说明,我们一直假设γ是一条C2可求长的正定向闭凸曲线,设其周长为L,所围区域面积为A.由引理2.1,存在唯一一个包含γ的最小圆环,记其中心为O,其内外圆周的半径分别为rin(O),rout(O).以O为坐标原点,任选一方向为极轴方向,建立极坐标系 {O;ρ(θ)}.

引理2.2[2]如果O是包含闭凸曲线γ的最小圆环的中心,则γ的Bonnesen函数

注 Bonnesen[1]在1921年提出了Bonnesen不等式,由文献[2]中(1.7)式可以得到此引理.

定理2.3 若ρ(θ)是按上述定义在C2闭凸曲线γ上的极坐标,则有

并且两个不等式取等皆当且仅当γ为圆周.

证

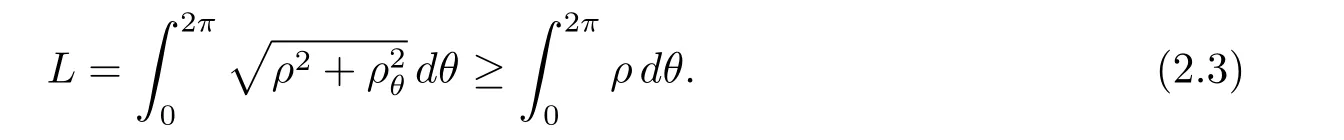
由于

再运用Cauchy不等式

定理2.4 若ρ(θ)是按上述定义在C2闭凸曲线γ上的极坐标,则有

并且该不等式取等当且仅当γ为圆周.

证 由于{O;ρ(θ)}是以包含γ的最小圆环的中心为原点,故

因此由引理2.2,

由此可得(2.6)式.

若γ为圆周,则ρ(θ)≡ 0,(2.6)式两边恒为0,故取等.反过来,若(2.6)式取等,则(2.9)式取等,由(2.8)式左边函数的连续性可知g(ρ)≡ 0,∀ρ∈[rin(O),rout(O)],因此rin(O)=rout(O),故γ为圆周.

定理2.5 若ρ(θ)是按上述定义在C2闭凸曲线γ上的极坐标,则有

若

由于{O;ρ(θ)}是以包含γ的最小圆环的中心为原点,故

由ε的任意性可得(2.10)式.

若γ为圆周,则ρ(θ)≡ 0,则(2.10)式两边恒为0,故取等.反过来,若(2.10)式取等,则由被积函数的连续性,因此rin(O)=rout(O),故γ为圆周.

推论2.6 若ρ(θ)是按上述定义在C2闭凸曲线γ上的极坐标,k为曲线γ的曲率,且则有

并且其中两个不等式取等皆当且仅当γ为圆周.

证 由于按照定理2.5的证明方法,可得(2.16)式左侧不等式,至于后面的不等式,可由Cauchy不等式

事实上,由椭圆极坐标形式