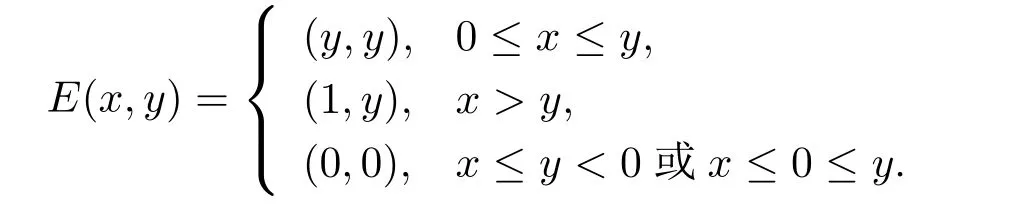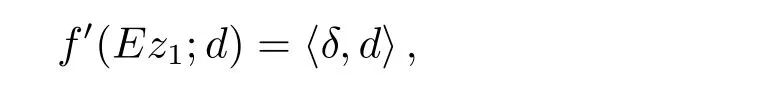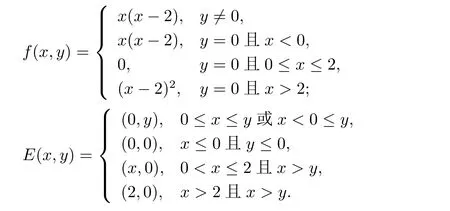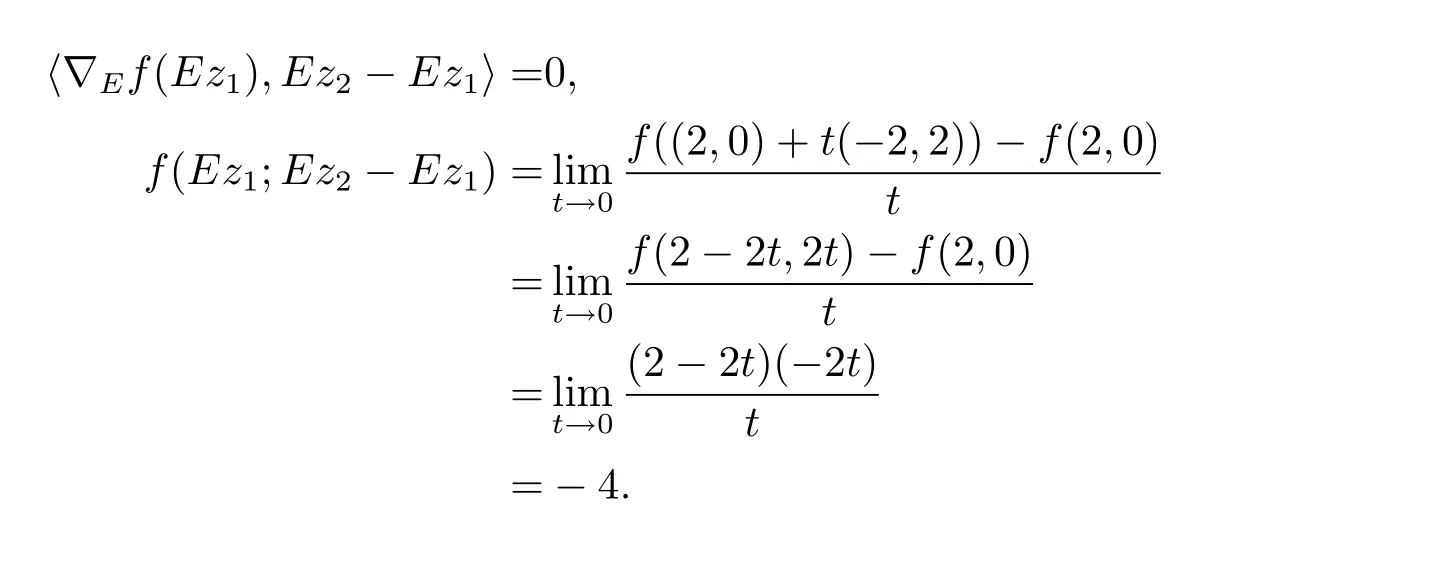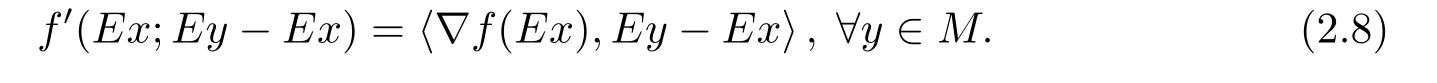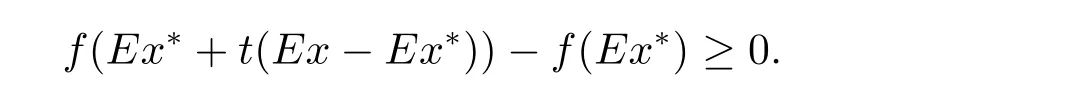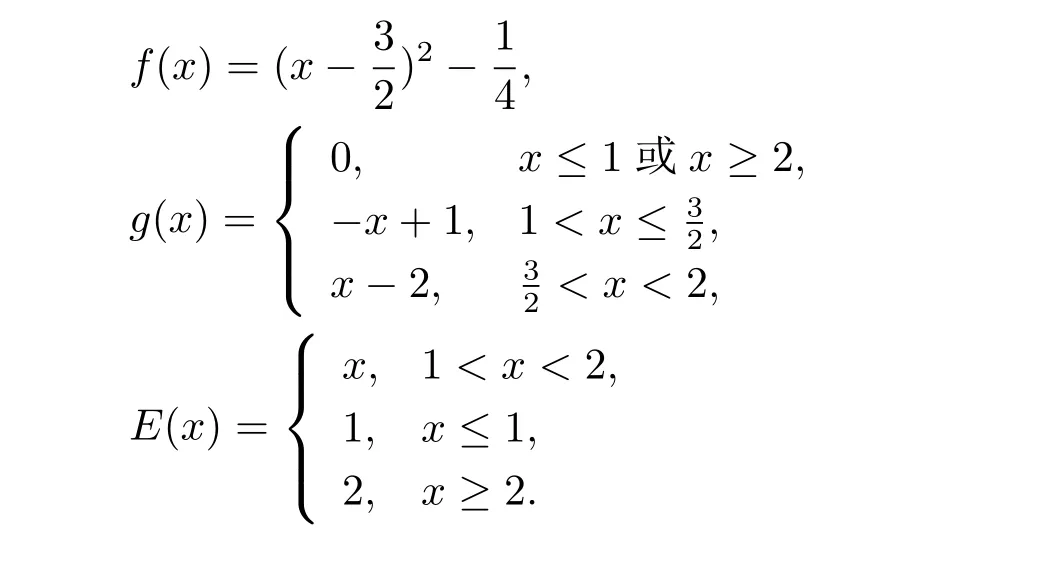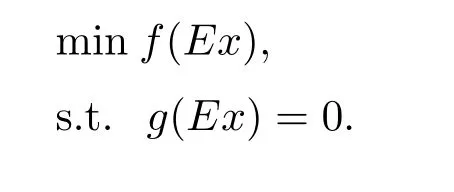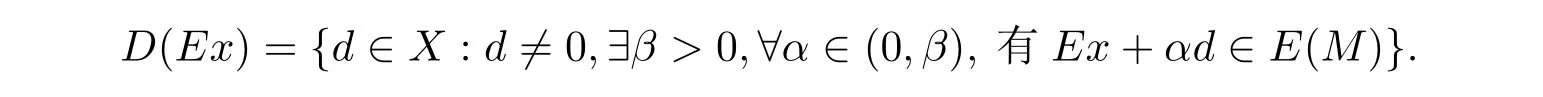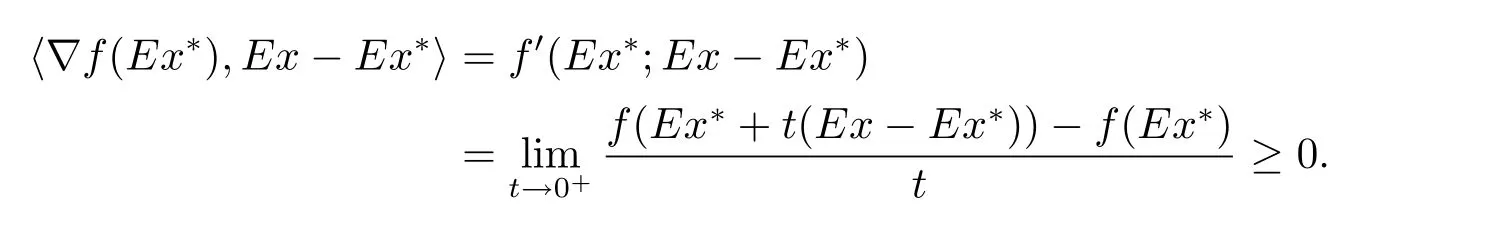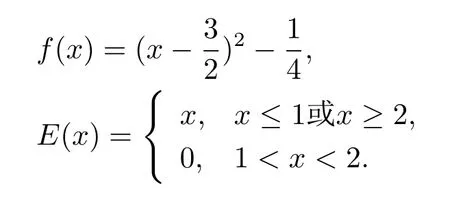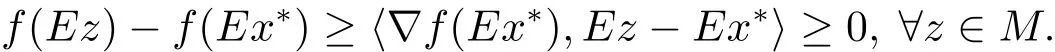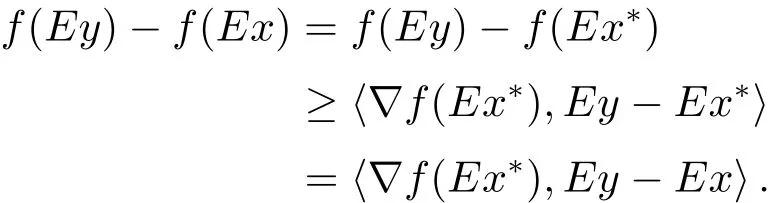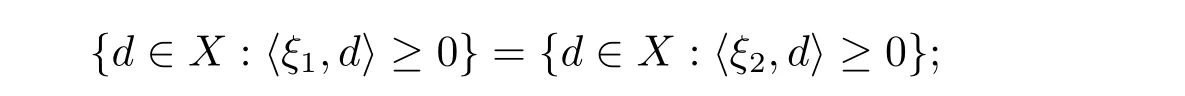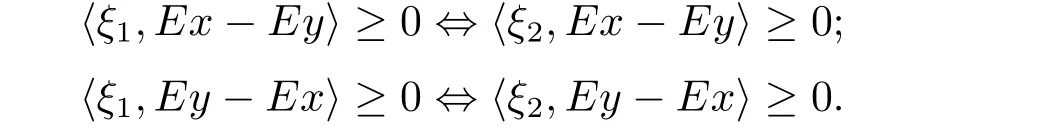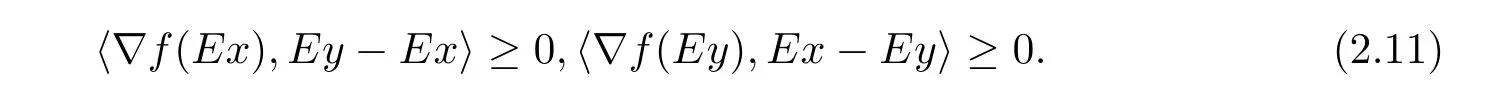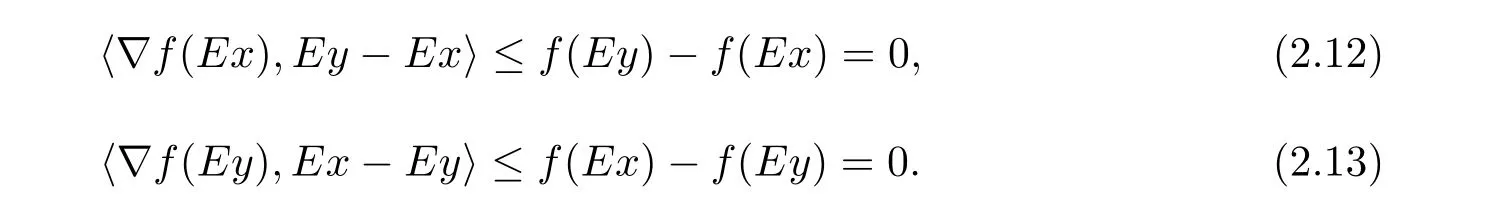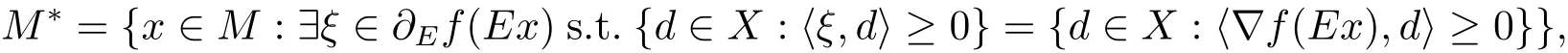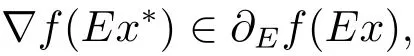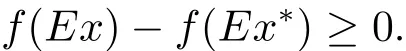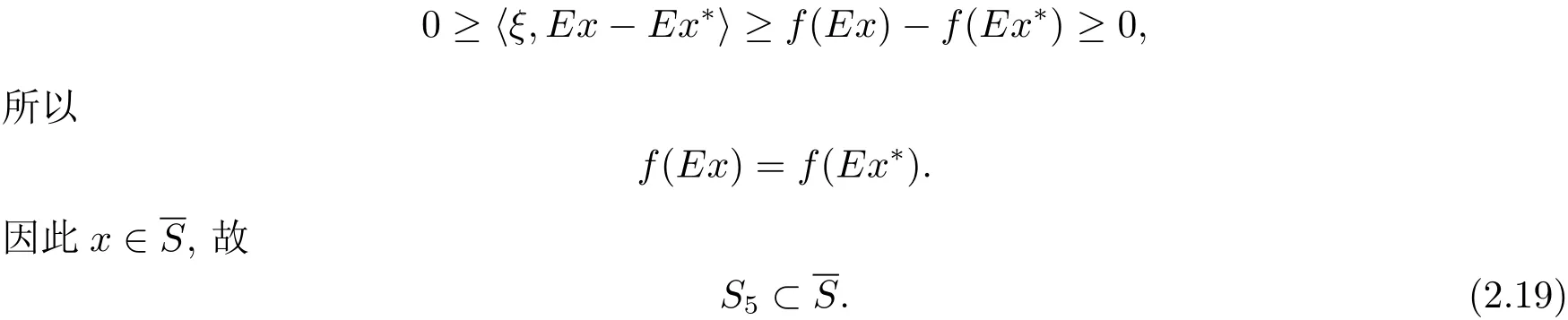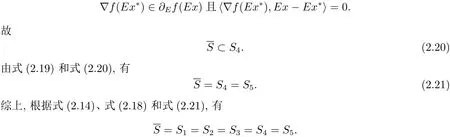Gateaux可微条件下E-凸规划问题的解集刻画

李 均,彭建文,刘学文

(重庆师范大学数学科学学院,重庆 401331)

1 引言

凸性条件无论是在数学还是经济、工程以及管理科学等领域,都起着至关重要的作用.然而现实生活中大部分的实际问题却难以满足凸性假设,因此广义凸性的研究就显得尤为必要.1999年,Youness在文献[1]中给出了如下的E-凸集、E-凸函数的概念.

定义1.1[1]称M ⊂X 为E-凸集,如果存在映射E:X →X,∀t∈[0,1]满足

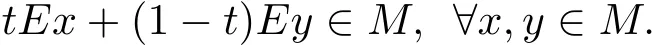
定义1.2[1]称f:X→R为集合M⊂X上的E-凸函数,如果存在映射E:X→X,使得M 为E-凸集,且∀t∈[0,1]有

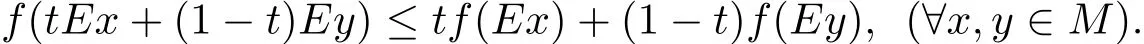
注1.1如果没有特别说明,本文假设X 代表赋范线性空间,X∗为其对偶空间,集合M ⊂X 均为开集.为了写作方便,本文中将E(x)都简写为Ex.当E=I(单位映射)时,定义1.1、定义1.2分别退化为文献[2]中凸集、凸函数的定义.

Youness在文献[1]中对E-凸函数性质进行了初步探索,Yang[3]和Chen[4]举例说明了文献[1]中定理4.2、定理4.3、定理4.6是错误的.最近,Youness在文献[5]中研究了如下带不等式约束的E-凸规划数学模型,简记为(COP)E:

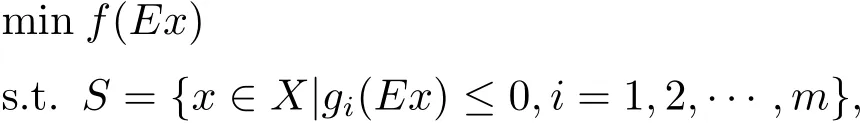
其中f,gi:X →R(i=1,2,···,m)都是X 上的E-凸函数.

在文献[5]中,Youness给出了多目标E-凸规划问题有效解的性质刻画.众所周知,在凸优化问题的研究中,次微分是一种重要的研究工具,Rockafellar在文献[6]中给出了凸函数次梯度的定义.

定义1.3[6]称ξ∈X∗为凸函数f:X→R在x∈X 处的次梯度,如果

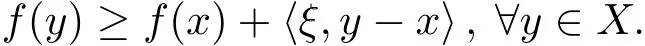
f在x处的次梯度的全体称为f在x处的次微分,记为∂f(x).

注1.2根据定义1.3,对任意y∈X,显然有

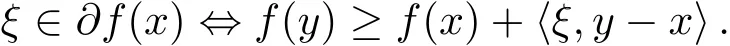
李成林等人在文献[7]中,利用Clarke的思想给出了E-凸函数E-次微分的定义及其等价刻画.

定义1.4[7]若M 是X中的E-凸集,f:M→R且x∈M∩dom(f),称ξ∈X∗是f在Ex处的E-次梯度,如果存在ε>0,η>0,使得∀Ey∈B(Ex,η)⊂M,有

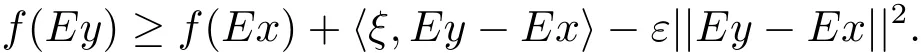
f在Ex处的E-次梯度的全体称为f在Ex处的E-次微分,记为∂Ef(Ex).

定理1.1[7]若f是E-凸集M ⊂X 上的E-凸函数,则∀x,y∈M,有

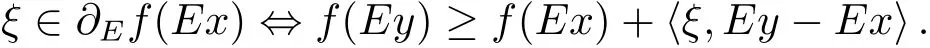
史树中在文献[2]中给出了函数的左、右方向导数及Gateaux可微的定义.

定义1.5[2]f:X→R是实值函数,x∈X,d∈X,

定义1.6[2]设f:X→R是实值函数,x∈X,若f0(x;d)对任意方向d都存在,且存在δ∈X∗使得f0(x;d)=hδ,di,∀d∈X.那么称f在x处Gateaux可微,并称δ为f在x处的Gateaux导数,记作δ=∇f(x).

注1.3文献[8]中给出了这样的结论:若凸函数f:X→R在x∈X处Gateaux可微,则有∂f(x)={∇f(x)}.

姜艮等人在文献[9]中给出了E-Gateaux可微的定义.

定义1.7[9]若M 是赋范线性空间X中的E-凸集,f:M →R是M 上的E-凸函数且x∈M ∩dom(f),称f在Ex处E-Gateaux可微,若有δ∈X∗,使得f0(Ex;d)=hδ,di,∀d∈E(X).若f在Ex处E-Gateaux可微,并称δ为f在Ex处的E-Gateaux导数,记作δ=∇Ef(Ex).

在文献[9]中,姜艮等人得到了如下的结论.

定理1.2[9]若X是赋范线性空间,M 是X上的E-凸集,f:M→R是M 上的E-凸函数且x∈M ∩dom(f),如果f在Ex处E-Gateaux可微,则∂Ef(Ex)={∇Ef(Ex)}.

定理1.3[9]若x∗是(COP)E的解,如果f在Ex∗处E-Gateaux可微,则∀x∈S,则有h∇Ef(Ex∗),Ex − Ex∗i≥ 0.

定理1.2和定理1.3是文献[9]的基础性定理,文献[9]中的其他结论都是基于这两个结论建立的,本文将举例说明这两个结论都是不正确的,并进一步研究如下的E-凸规划问题

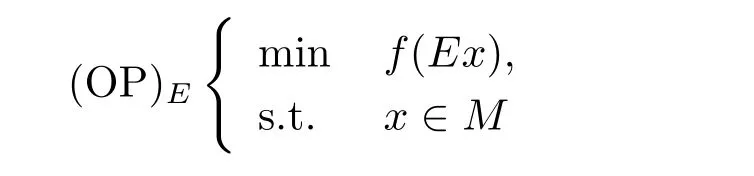
在Gateaux可微条件下最优解集的性质定理及最优解集等价刻画,其中f:M →R是E-凸函数.

2 主要内容

在定理1.2的证明中有

式(2.1)显然是错误的,因为Ez只能取遍E(M),不一定能取遍全空间X.下面例2.1说明式(2.1)是错误的.

例2.1令X=R2,M={(x,y):0

函数f:X→R定义为f(x,y)=c(常数).容易验证M 为E-凸集,f为M 上的E-凸函

情形1 当x≤ y时,则Ez=(y,y),设ξ=(ξ1,ξ2),由定理1.1,要使得ξ∈∂Ef(Ez1),ξ必须满足

情形2 当x>y时,则Ez=(1,y),设 ξ=(ξ1,ξ2),由定理1.1,要使得 ξ∈ ∂Ef(Ez1),ξ必须满足式(2.2),于是有

结合式(2.3)和式(2.4)可求得满足式(2.2)的ξ必须满足下面的条件:

又因为y∈(0,1),所以ξ∈∂Ef(Ez1)必须满足ξ2≥0且ξ1+ξ2=0.故

再计算∇Ef(Ez1).根据定义1.7,设δ=(δ1,δ2),要使δ=∇Ef(Ez1),必须满足下面的条件:

即 0= δ1+δ2λ, ∀λ ∈ R.所以 δ=(0,0),故

由式(2.5)和式(2.6)知{∇Ef(Ez1)}6=∂Ef(Ez1).

在定理1.2的证明中使用了如下语句

因为f在Ex处E-Gateaux可微=⇒f0(Ex;Ey−Ex)=h∇Ef(Ex),Ey−Exi. (2.7)并由式(2.7)证得∇Ef(Ex)∈∂Ef(Ex),但是式(2.7)是错误的,其原因在于Ey−Ex∈E(X)一般不成立.下面例2.2说明式(2.7)是不正确的.

例 2.2 令X=R2,M={(x,y):−1

容易验证M 为E凸集,f为M 上的E凸函数,d=(2,0)或d=(0,λ),(λ∈R+)为E(X)中的任意方向.这里特别取z1=(2,1),则Ez1=(2,0),显然可得f在Ez1处E-Gateaux可微且∇Ef(Ez1)=(0,0).令z2=(1,2),则Ez2=(0,2),此时Ez2−Ez1=(−2,2)/∈E(X),而显然f0(Ez1;Ez2−Ez1)6=h∇Ef(Ez1),Ez2−E1i.

定理1.2可以被纠正为如下的结论.

定理2.1 X是赋范线性空间,M 是X上的E-凸集,f:M→R是M 上的E-凸函数且x∈M∩dom(f),如果f在Ex处Gateaux可微,则∇f(Ex)∈∂Ef(Ex).

证 因为f在Ex处Gateaux可微,由定义1.6,则有

又因为f:M→R是M 上的E-凸函数,则有

在上式中取t→0+,则有

于是由式(2.8)和式(2.9)知

由定理1.1,故∇f(Ex)∈∂Ef(Ex).

注2.1 若f在Ex处Gateaux可微,∂Ef(Ex)={∇f(Ex)}不一定成立.在例2.1中,函数f在处Gateaux可微,且∇f(Ez1)=(0,0),但是f在Ez1处的E-次微分是

在定理1.3的证明中存在:x∗是(COP)E的解,则对t∈[0,1],有

该结论是不正确的,其原因是这里并未能保证Ex∗+t(Ex−Ex∗)∈E(S).下面的例2.2说明定理1.3是错误的.

例2.3 令X=R,函数f,g:X→R,映射E:X→X分别定义为

这里E-凸规划问题(COP)E为

容易验证函数f,g都是X 上的E-凸函数,E(X)中的方向只有d=1,且可求得(COP)E问题可行域S={x∈R:x≤1或x≥2}.经验证x=1或x=2为(COP)E问题的最优解.这里特别取x∗=2为(COP)E问题的一个最优解,根据定义1.7可以求得∇Ef(Ex∗)=1.但是存在点x=1,则Ex=1,使得h∇Ef(Ex∗),Ex−Ex∗i=1×(1−2)=−1<0.从而知定理1.3的结论不一定成立.

文献[10]中介绍了可行方向锥的概念,这里给出E-可行方向锥的概念.

定义2.1集合M ⊂X 为E-凸集,x∈M,记Ex处的E-可行方向锥为

将定理1.3纠正为如下的定理.

定理2.2若x∗是(OP)E的解,f在Ex∗处Gateaux可微,且对x∈M,有Ex−Ex∗∈D(Ex∗),则 h∇f(Ex∗),Ex −Ex∗i≥ 0.

证 因为x∗是(OP)E的解,Ex−Ex∗∈D(Ex∗),则存在β>0,使得∀t∈(0,β),有Ex∗+t(Ex−Ex∗)∈ E(M)且 f(Ex∗+t(Ex−Ex∗))−f(Ex∗)≥ 0.又因为 f 在 Ex∗处Gateaux可微,则有

即 h∇f(Ex∗),Ex−Ex∗i≥ 0.

用下面的例子来说明定理2.2的合理性.

例2.4 这里取M=R,函数f与映射E分别定义如下

易知x=1或者x=2为(OP)E的最优解,下面讨论x∗分别取1和2时的情况.

情形1 当x∗=1时,则Ex∗=1,f在Ex∗=1处Gateaux可微且∇f(Ex∗)=−1,此时可求得f在Ex∗处的可行方向锥为D(Ex∗)={d∈X:d<0}.当x<2且x 6=1时,有Ex−Ex∗∈ D(Ex∗),因此 h∇f(Ex∗),Ex−Ex∗i≥ 0.

情形 2 当x∗=2时,则Ex∗=2,f在Ex∗=2处Gateaux可微且∇f(Ex∗)=1,此时可求得f在Ex∗处的可行方向锥为D(Ex∗)={d∈X:d>0}.当x>2时,有Ex−Ex∗∈ D(Ex∗),因此 h∇f(Ex∗),Ex−Ex∗i≥ 0.

下面给出E-凸规划问题(OP)E的一个性质定理.

定理2.3若f:M→R上E-凸函数,S为(OP)E规划的最优解集,x∗∈且满足f在Ex∗处Gateaux可微且∀z∈M都有Ez−Ex∗∈D(Ex∗),则∇f(Ex∗)

证 因为f在Ex∗处Gateaux可微,由定理2.1可得∇f(Ex∗)∈∂Ef(Ex∗).又由定理2.2,有

取 z=x,则 h∇f(Ex∗),Ex−Ex∗i=0,由上式知,∀y ∈ M,有

由定理1.1可得∇f(Ex∗)∈ ∂Ef(Ex).因此∇f(Ex∗)

定理2.4若M是赋范线性空间X中的E-凸集,且f:M→R是M上的E-凸函数,则(1)⇒(2)⇒(3)⇒(4)⇒(5),其中(1),(2),(3),(4),(5)的定义分别为

(1) 存在 ξ1∈ ∂Ef(Ex),ξ2∈ ∂Ef(Ey),满足 hξ1,Ex−Eyi=0,hξ2,Ex−Eyi=0;

(2) 存在 ξ1∈ ∂Ef(Ex),ξ2∈ ∂Ef(Ey),满足 hξ1− ξ2,Ex−Eyi≤ 0;

(3) ∂Ef(Ex)∩ ∂Ef(Ey)6= φ;

(4) 存在 ξ1∈ ∂Ef(Ex),ξ2∈ ∂Ef(Ey),满足

(5) 存在 ξ1∈ ∂Ef(Ex),ξ2∈ ∂Ef(Ey),满足

进一步,若x,y是(OP)E的解,f在点Ex,Ey处Gateaux可微且Ex−Ey∈D(Ey),Ey−Ex∈D(Ex),则(5)⇒(1).

证 (1)⇒ (2)⇒ (3)⇒ (4)可以参见文献[9]的定理2.3,这里(4)⇒ (5)直接取d=Ex−Ey即可.下证(5)⇒(1).

因为f在Ex,Ey处Gateaux可微且Ex−Ey∈D(Ey),Ey−Ex∈D(Ex),根据定理2.2有

又因为x,y是(OP)E的解,再由定理1.1和定理2.1,则

由式(2.11)–(2.13)可知,这里取ξ1=∇f(Ex),ξ2=∇f(Ey)即满足(1).

最后给出E-凸规划问题(OP)E最优解集的几种等价刻画.

证 首先证明S3=S4=S5.根据定义,S3⇒S4⇒S5显然成立.

下证S5⊂ S3,若x∈S5,存在ξ∈∂Ef(Ex)使得hξ,Ex−Ex∗i≤ 0由定理1.1,定理2.1和定理2.2,有

对任意的y∈M,由定理1.1及定理2.1可得

再根据定理1.1有

故

由式 (2.15)–(2.17),有

再证S5⊂S⊂S4.

设x∈S5,因为x∗∈S,所以

又因为存在ξ∈∂Ef(Ex)使得hξ,Ex−Ex∗i≤0,由定理1.1有

设x∈S,由定理2.3的证明可知