求一类p(t)-Laplace中立型微分泛函方程解的存在性

于 美,马国祯

(西北工业大学理学院,陕西西安 710072)

1 引言

近年来,随着自然科学和工程技术中许多非线性问题的不断出现,Sobolev空间表现出了其应用范围的局限性.例如,对一类有变指数增长条件的非线性问题的研究.具有变指数增长性条件的非线性问题是一个新兴的研究课题.在对这类非线性问题进行研究时,变指数Lebesgue空间及Sobolev空间发挥着重要的作用[1−4].

在本文中,我们主要研究一类p(t)-Laplace中立型微分泛函方程

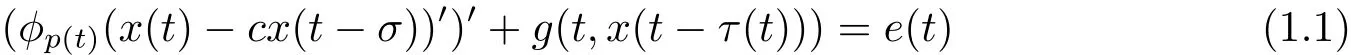
周期解的存在性,其中 φp(t):R → R,φp(t)(u)=|u|p(t)−2u,g∈C(R2,R),1

由于指数p(t)为函数,p(t)-Laplace算子较之p-Laplace具有更复杂的非线性性,许多对于p-Laplace问题成立的方法和结果不再适用于p(t)-Laplace问题.本文结合了Mawhin连续定理与不等式技巧的应用,克服了变指数p(t)产生的困难,得到了新的研究成果.关于常指数增长条件下的周期解存在性的问题,可参考文献[5–6].

2 预备知识

首先回忆一些关于变指数Lebesgue空间Lp(t)(Ω)的定理[7].

定义2.1设P是所有Lebesgue可测函数集,且p:Ω→(1,∞).对于p(t)∈P(Ω),设

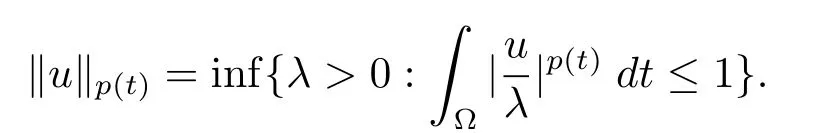
变指数Lebesgue空间Lp(t)(Ω)是由一类满足的函数u组成,且Lp(t)(Ω)是由上述范数诱导的Banach空间.定义p(t)∈P(Ω)的共轭函数q(t)为q(t)=

定理2.2令p∈P(Ω),那么

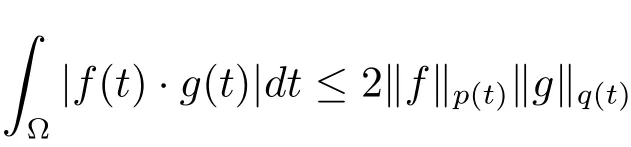
对于每个f∈Lp(t)(Ω)和g∈Lp0(t)(Ω)都成立.

定理2.3设u,uk∈Lp(t)(Ω),则

对于Mawhin连续性定理[8].令X,Y是实Banach空间,L:D(L)⊂X→Y是一个Fredholm算子并且指数为0,D(L)是L的值域,这意味着ImL在Y上是一个闭域并且有

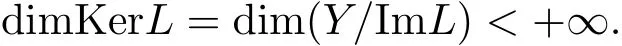
考虑补充子空间X1,Y1,其中X=KerL⊕X1,Y=ImL⊕Y1.令P:X→KerL,Q:Y→Y1是自然投影.显然有KerL∩(D(L)∩X1)={0}.因此限制条件LP:=L|D(L)∩X1是可逆的,由K表示LP的逆.

令Ω是X的一个开的有界子集并且D(L)∩Ω 6=φ.如果QN(¯Ω)是有界的,算子K(I−Q)N:¯Ω→X是致密的,则在¯Ω中N:¯Ω→Y是L-紧致的.

引理2.4假设X,Y是两个Banach空间,L:D(L)⊂X→Y是一个Fredholm算子并且指数为0.此外Ω⊂X是一个开的有界集合,在¯Ω上N:¯Ω→Y是L-紧致的.如果有

(1)Lx 6= λNx,∀x∈ ∂Ω ∩D(L),λ ∈ (0,1).

(2)Nx/∈ImL,∀x∈∂Ω∩KerL.

(3)deg{JQN,Ω∩KerL,0}6=0,其中J:ImQ→ KerL是同构的.则Lx=Nx在¯Ω∩D(L)上有一个解.

引理2.5如果|c|6=1,且A在CT上有连续有界映射,那么

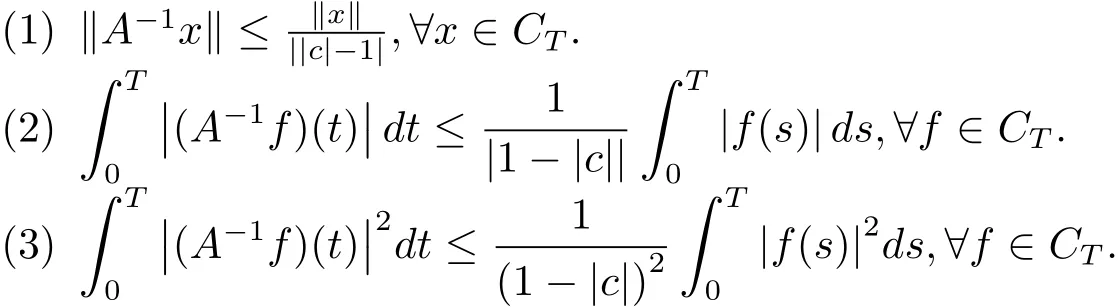
3 周期解的存在性

首先把方程(1.1)写成如下形式

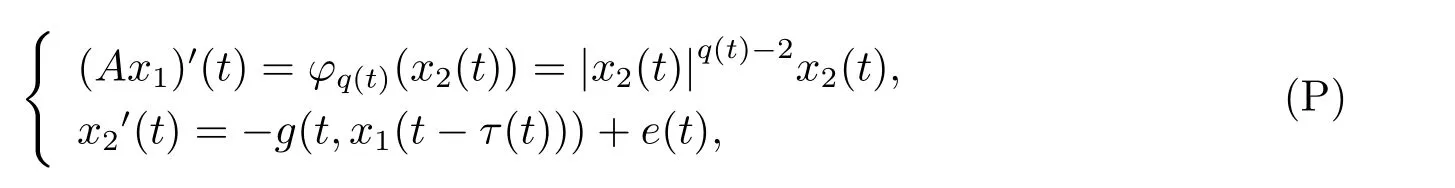
假设T是一个大于0的常数CT={ϕ:ϕ∈C(R,R),ϕ(t+T)≡ϕ(t)}且具有范数|ϕ|0=|ϕ(t)|,X=Y ={x=(x1(t),x2(t))∈ C(R,R2):x(t+T)≡ x(t)} 具范数kxk=max{|x1|0,|x2|0},显然X 和Y是Banach空间.令

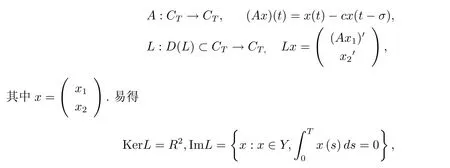
所以L是一个指标为零的Fredholm算子.

令投影P:X→KerL与Q:Y→ImQ定义如下

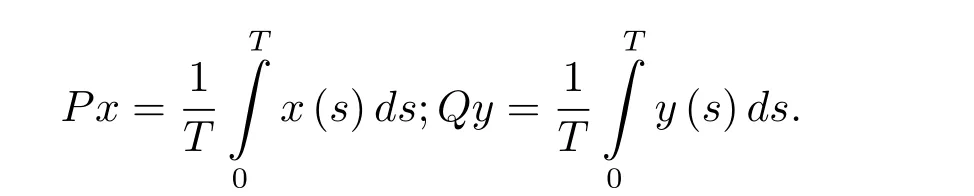
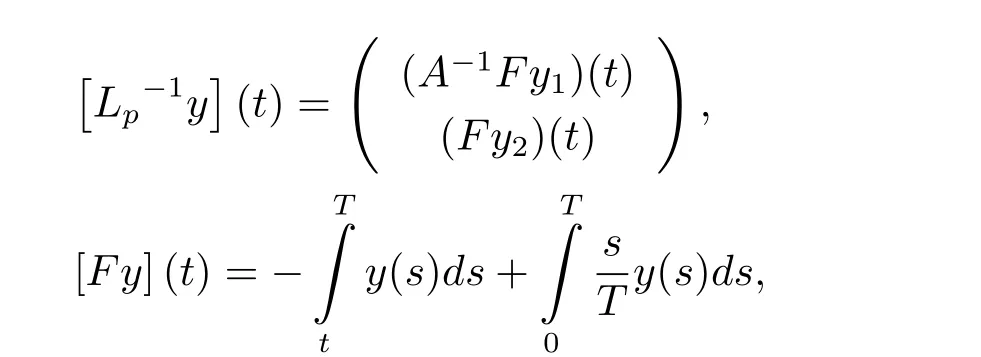
3.1 假设条件

给出以下假设条件

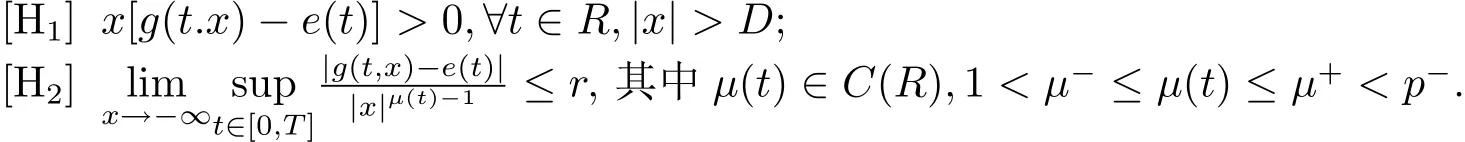
3.2 主要结论及证明

引理3.1如果p(t)>2且存在正常数D,r≥0满足[H1]–[H2],则(1.1)至少有一个T型周期解.

证 显然当且仅当Lx=Nx成立时,方程(P)有T型周期解,其中N:CT→CT,

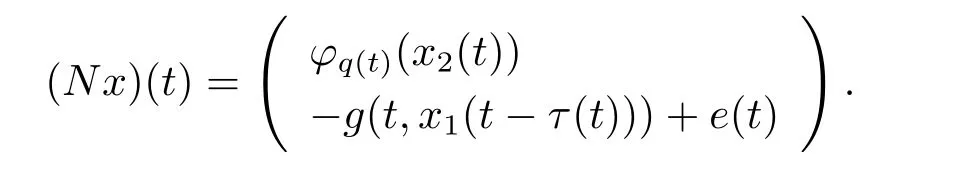
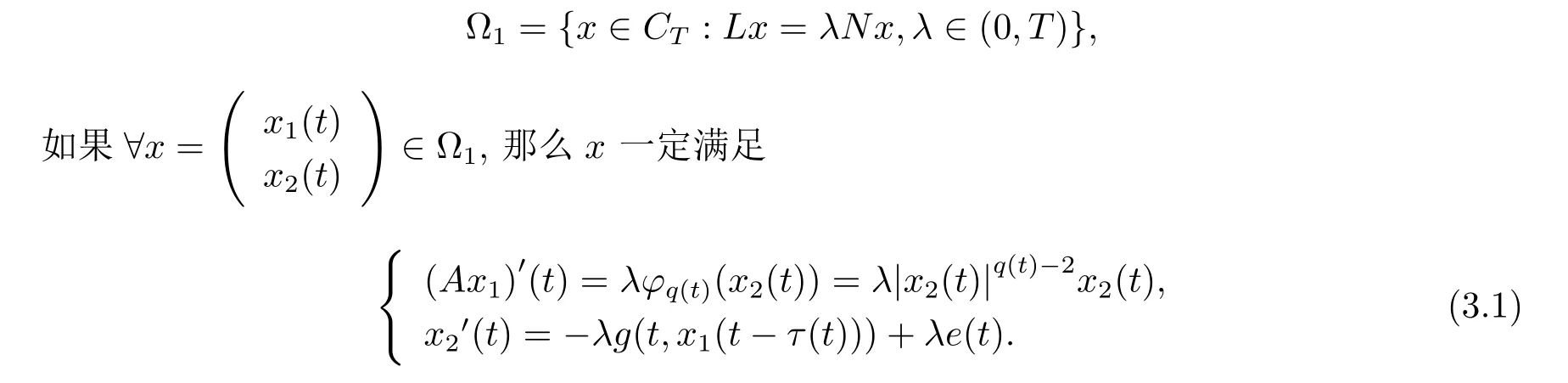
由(3.1)式的第一个等式可得x2(t)=Ax1)0(t)),将其代入(3.1)式的第二个等式,可得

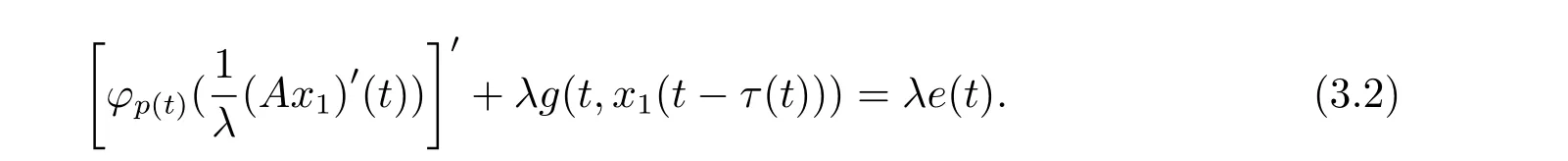
在区间[0,T]上积分(3.2)式的两边,由牛顿-莱布尼兹定理,可得

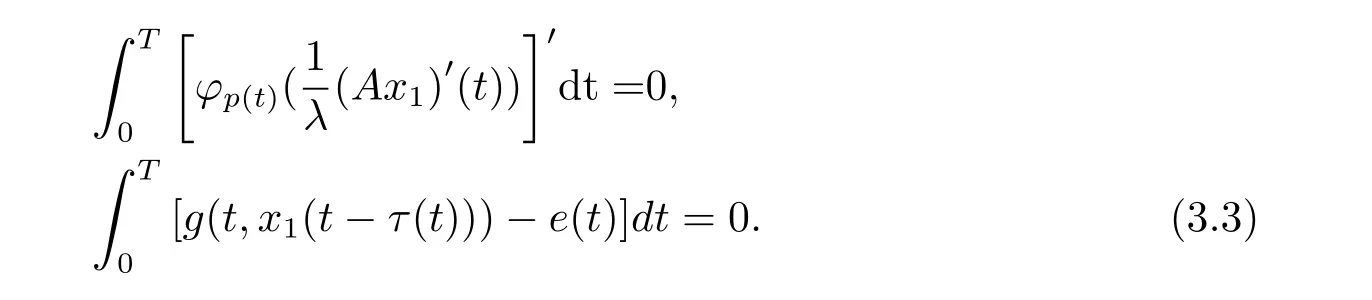
由积分中值定理,存在常数ξ∈[0,T]满足g(ξ,x1(ξ−τ(ξ)))−e(t)=0.由假设[H1]可得|x1(ξ− τ(ξ))|≤ D.令 ξ− τ(ξ)=kT+t0,其中 k ∈ Z,t0∈ [0,T),因此

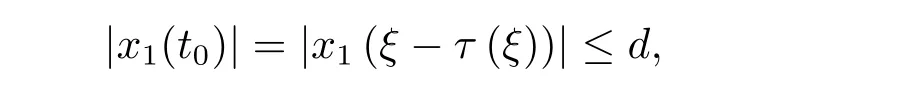
这意味着

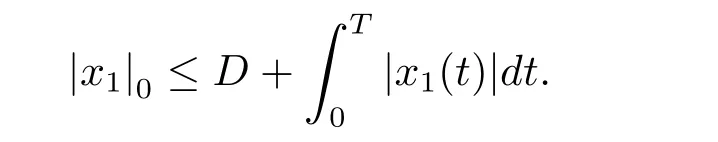
另一方面,将(3.2)式两端同时乘(Ax1)(t),可得

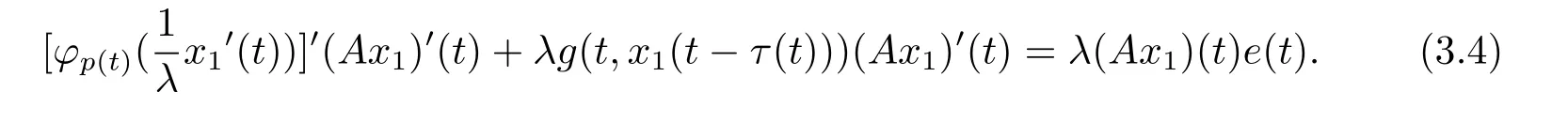
在区间[0,T]上积分(3.4)式的两边,由于

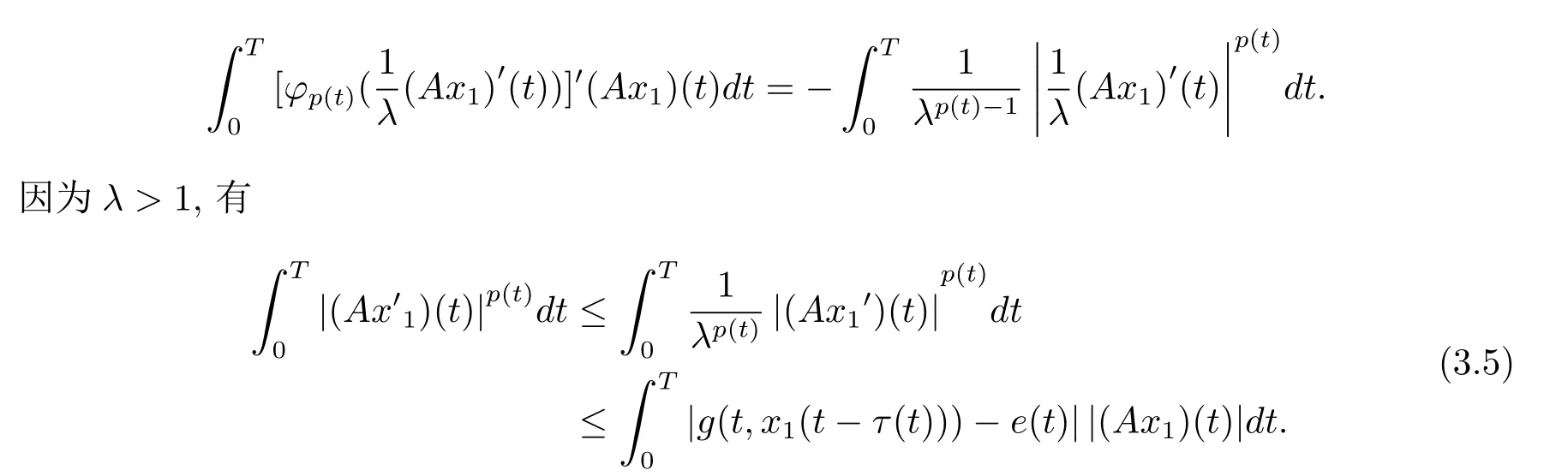
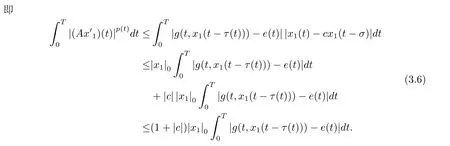
由假设[H2]可知,∃ρ>0满足

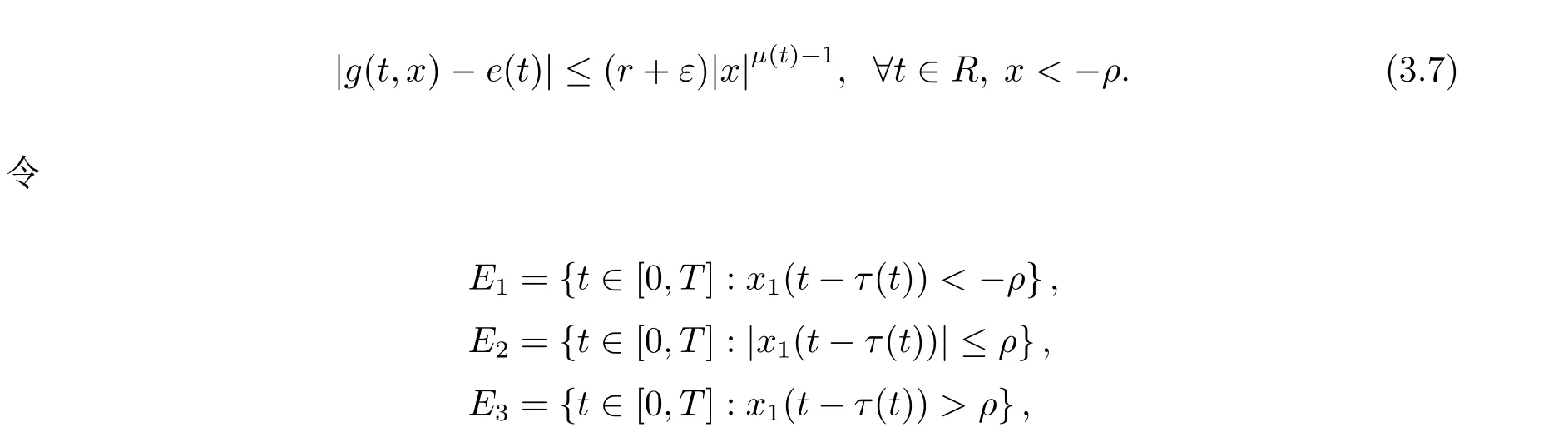
由(3.3)式可得

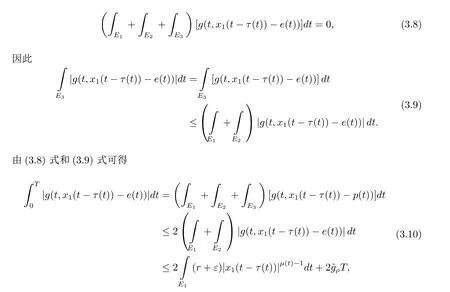
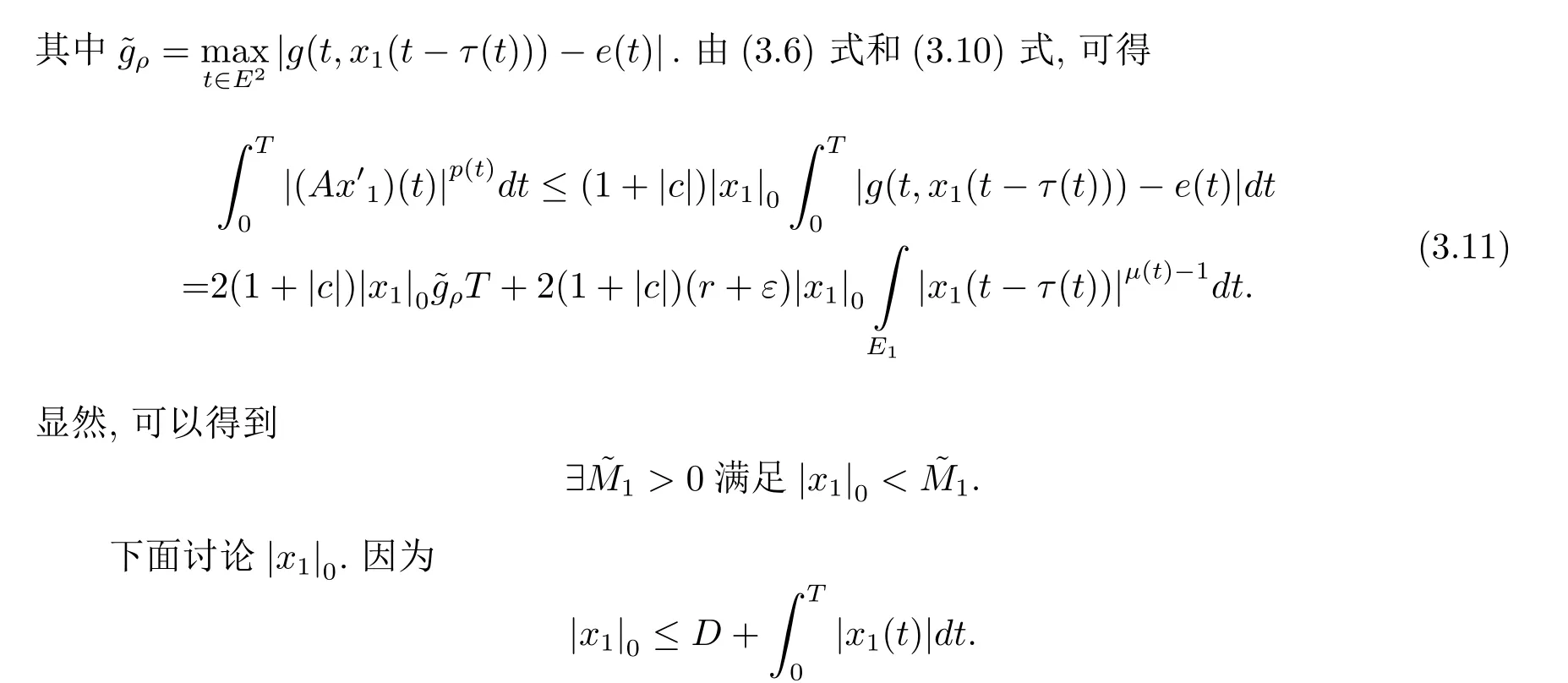
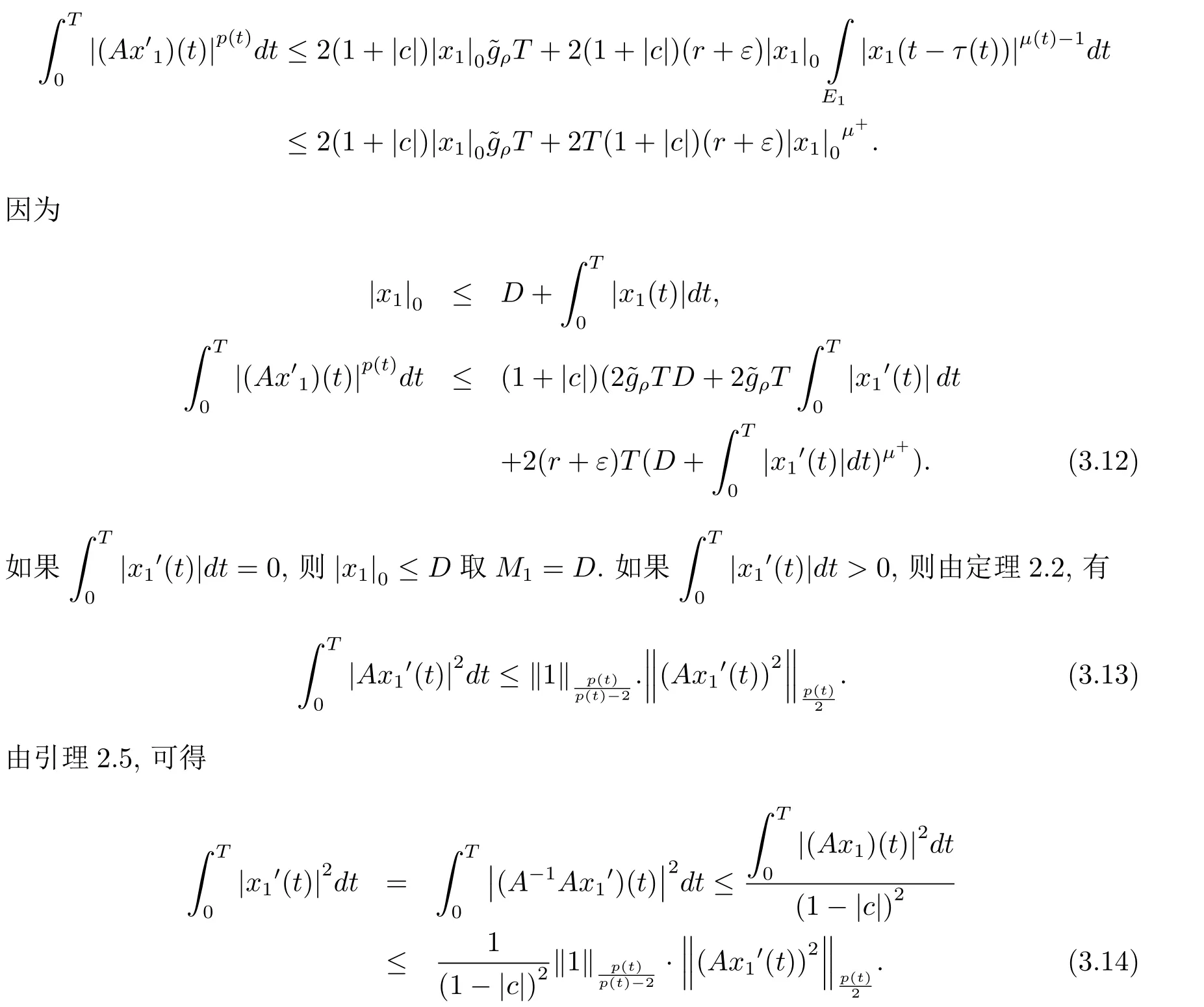
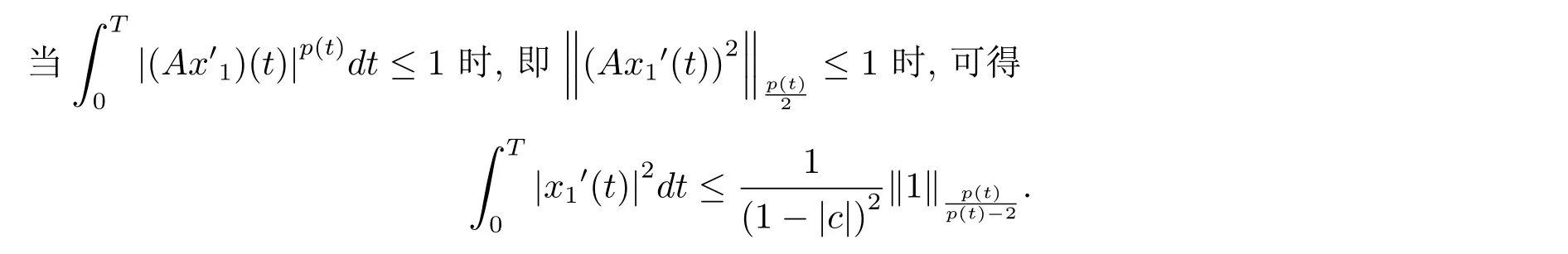
由于µ+<2可得,存在C>0,使得因此|x1|0≤ D+C+T=M1.综上所述,∃M1>0,使得|x1|0

下面讨论|x2|0的边界.由(3.1)式的第一个等式,可知这意味∃t1∈[0,T]着满足x2(t1)=0,因此dt.由(3.2)式的第二个等式可得

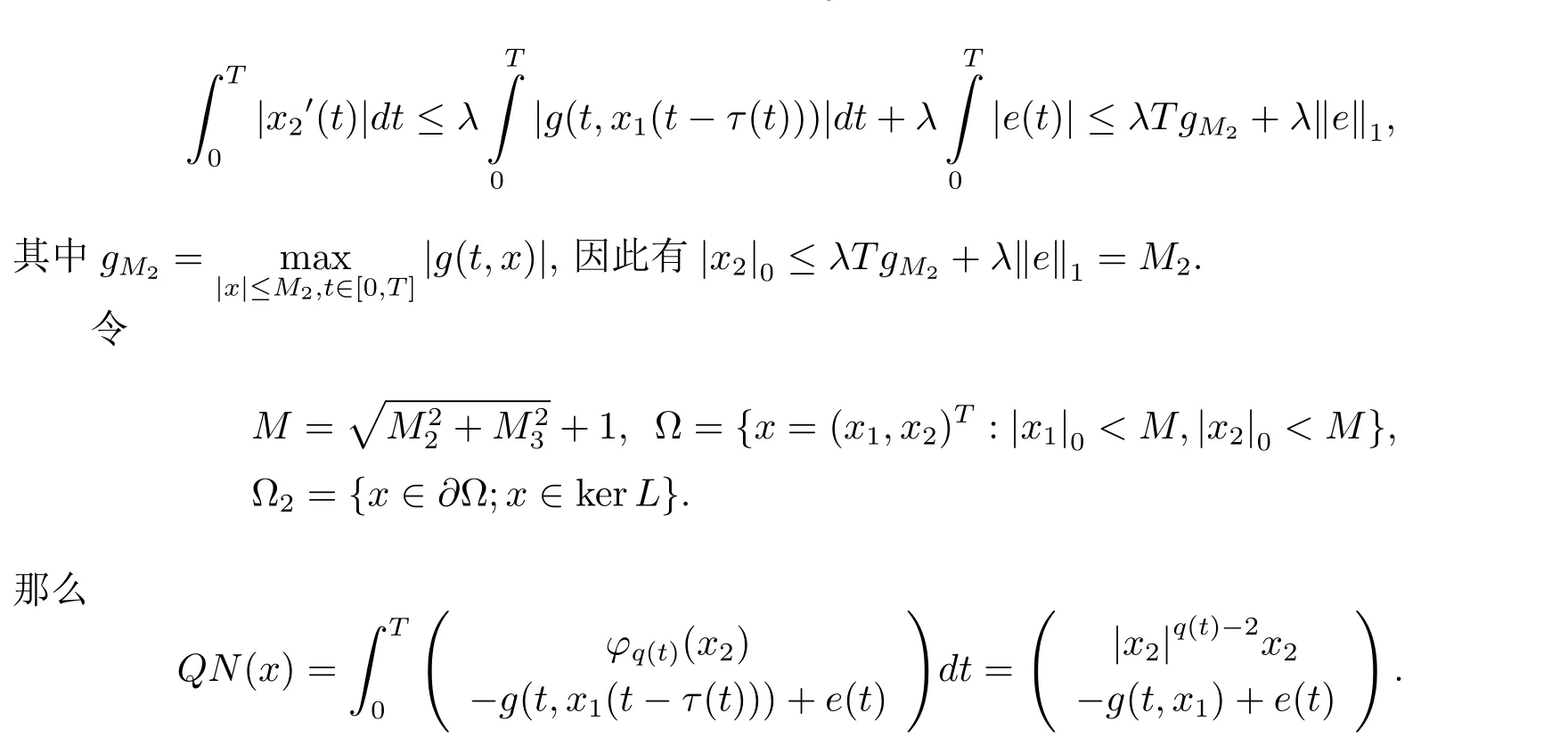
若QNx=0,那么x2=0,x1=M,或=M.但是当x1=M 时,显然−g(t,x1)+e(t)<0矛盾.当x1=−M时,显然QNx 6=0,∀x∈Ω,x/∈ImL,因此引理2.4中(1)和(2)均得到满足.

下面证明引理2.4(3)同样成立.定义同构:J:ImQ→kerL:J(x1,x2)T=(x2,x1)T.

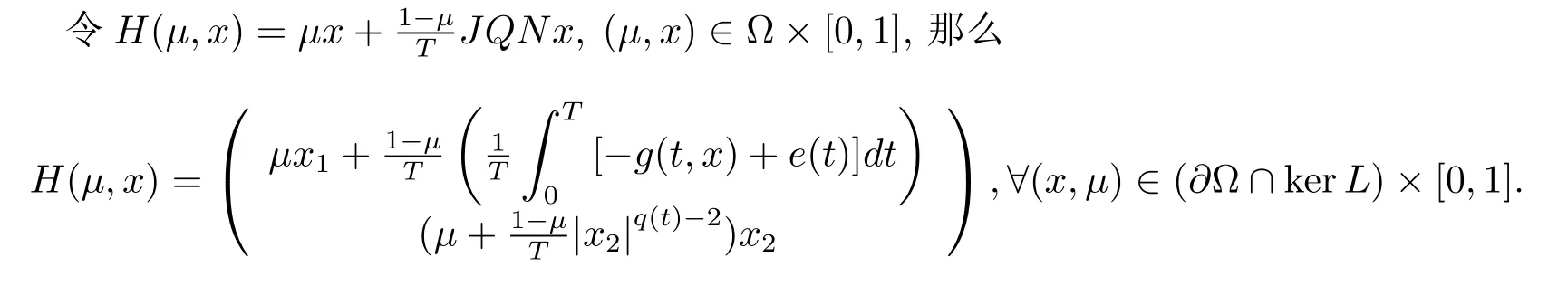
如果H(µ,x)=0,那么x2=M或−M.与上面的证明类似,也可证明H(µ,x)6=0.因此

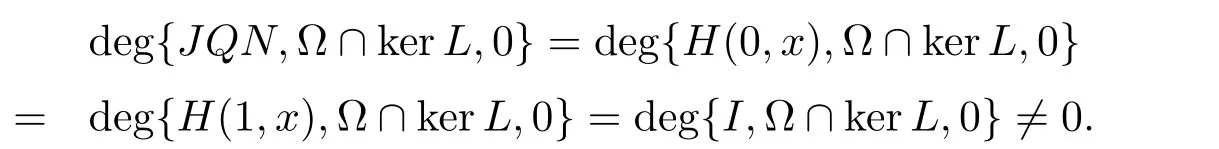
因此引理2.4的以三个条件同样成立.应用引理2.4,可得Lx=Nx在上有一个解几乎处处成立,方程(1.1)存在一个周期解.