基于改进遗传算法的机器人时间最优轨迹规划

秦 律，汪木兰，朱晓春，王保升

(南京工程学院江苏省先进数控技术重点实验室，江苏 南京 211167)

随着智能制造的深入发展，具备焊接、码垛、搬运等功能的串联机器人因其结构简单、制造成本低廉、控制便捷等优点，被广泛应用于工业自动化生产线[1-2]。轨迹规划作为机器人运动控制的基础，对研究机器人的运行效率、作业精度和工作平稳性具有重要意义。为寻求轨迹最优解，可分别对能量、时间、冲击等机器人工作指标进行局部优化，或者综合考虑上述指标以获取全局最优[3]。

对机器人运行时间的最优化求解为当前的研究热点，其中较为成熟的时间优化算法有人工神经网络算法、遗传算法、粒子群算法和蚁群算法[4]。文献[5]提出了一种改进型免疫克隆优化方法，以拥挤距离确定克隆规模大小来保留最优解，采用亲和度较高的个体代替消亡个体，加速种群的收敛速度。文献[6]采用序列二次规划方法求解在非线性约束条件下的最短时间，在目标函数进行迭代时，以牛顿法得到的拉格朗日函数构成的Hessian矩阵来实现收敛，但该方法判断收敛的条件复杂，降低了寻优效率，并且不能保证局部轨迹的精度。文献[7]采用自适应遗传算法进行时间优化，通过调整后期变异概率，增加种群的多样性。但利用罚函数处理运动学约束时，不满足约束的个体所受惩罚量较大，易出现适应度值较大的特殊个体引导种群发展，导致寻优过程陷入局部最优并过早收敛。

本文在用三次样条函数对机器人轨迹进行插值的基础上，采用聚类方法改进的遗传算子对个体适应度值大小进行分类，制定不同选择方法，保留优良个体并兼顾种群多样性。以新的变异操作对后期的最优个体进行调整，提高搜索效率，求出机器人的最短工作时间。

1 三次样条插值规划

三次样条插值函数的剖分子区间均为三次多项式，通过给定边界条件对各型值点进行插值拟合。将其运用于机器人轨迹规划中，既保证了机器人关节位移和速度的连续性，又能防止关节角加速度的突变，使机器人运行平稳且避免震动。

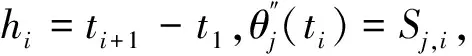
(1)

(2)

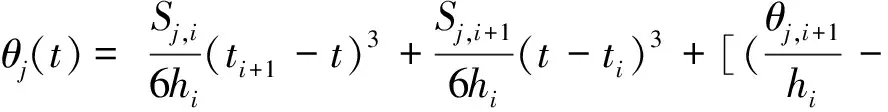
(3)

对式(1)进行微分，求出相应时间段的关节角加加速度，即：

(4)

(5)

(6)

依此类推，将式(5)写成矩阵形式得：

(7)

式中：方程组的系数矩阵为三对角矩阵，由于|λi|+|μi|=1，则|λi|+|μi|，|λi|,|μi|三者均小于主对角元素2，所以系数矩阵为严格对角占优矩阵。通过追赶法求得Sj,1,Sj,2,…,Sj,n的数值，代入式(3)，得到完整的关节角位移表达式。

2 多目标优化函数

通过三次样条函数，使机器人能对关节的角位移、角速度与角加速度进行实时控制。考虑到提高机器人的运行效率，还需要对各关节的运行时间进行优化，使机器人能够高效地完成工作任务。

将机器人运动的整段轨迹曲线按选取的型值点进行剖分，通过对各分段轨迹的时间优化来达到总时间的最优，即：

(8)

式中:Tmin为机器人完成整段轨迹曲线所需最短时间。机器人关节在进行轨迹规划运动时还会受速度、加速度、加加速度的约束，即：

(9)

3 时间最优轨迹规划

遗传算法是在进化论和自然遗传机制上衍生的搜索方法，相对于传统优化算法，具有全局性、并行性、灵活性等特点。本文利用基于聚类方法的遗传算法[8-9]，对进行三次样条插值后的关节轨迹进行时间优化，在保证种群多样性的同时，加强了局部搜索能力。其具体算法流程如图1所示。

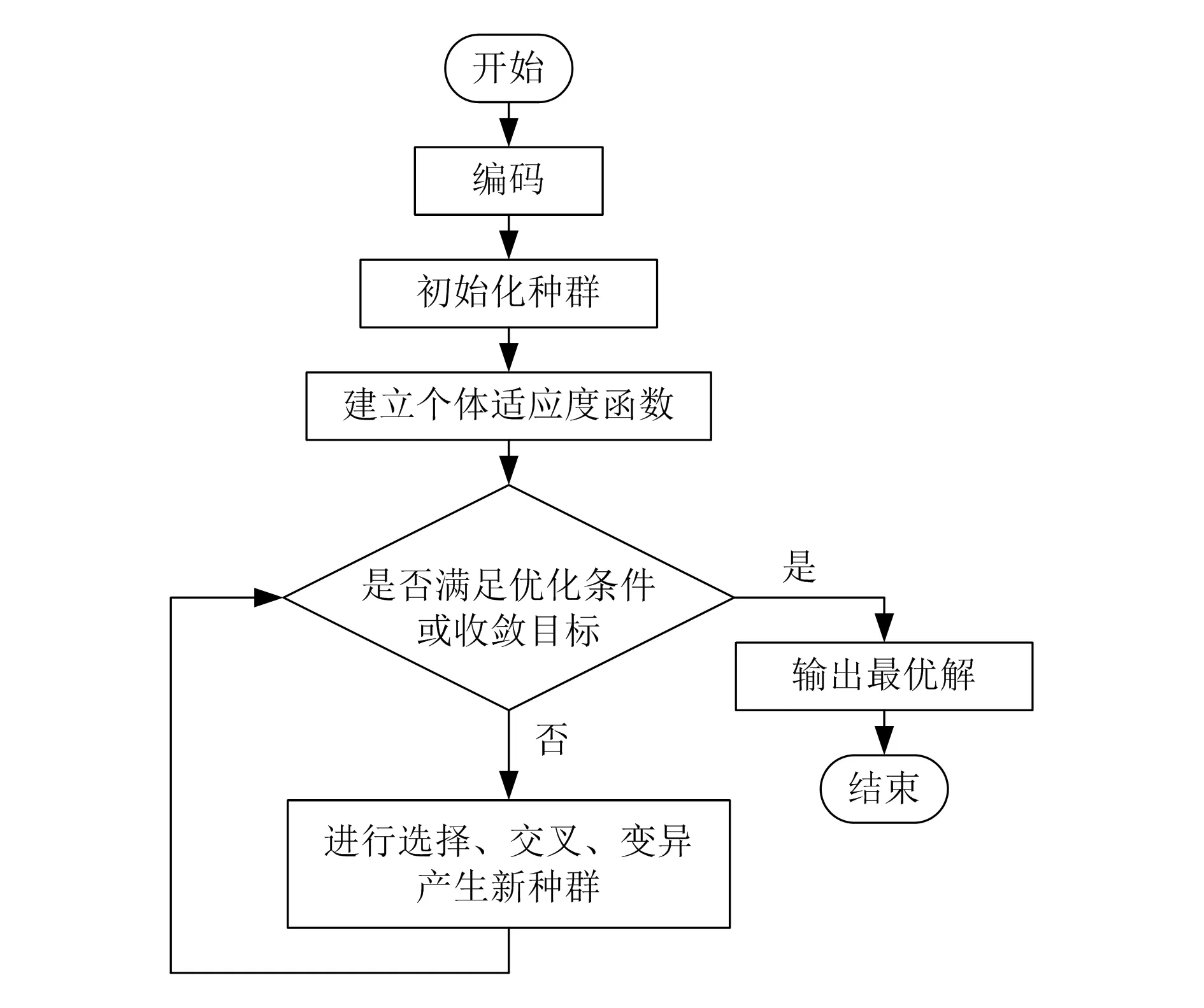
图1 基于聚类方法的遗传算法流程图

1)编码。

对各分段轨迹曲线的运动时间进行二进制编码，设定编码长度，使可行解的精度为0.001。该操作简单易行，使交叉、变异等遗传操作便于实现。

2)种群初始化。

在满足约束条件的情况下，对种群进行初始化，在hi的值域内，随机生成多个新个体，并设置种群的规模为m。为保持种群的多样性，并方便后续的适应度值分类，m选取20～100之间的奇数。

3)适应度函数建立与标定。

用外罚函数法处理式(9)中的不等式约束条件，通过对不满足约束条件的个体施加惩罚项，并随着种群的发展，增大惩罚量，迫使迭代点逐步向可行域靠近。其表达式如下：

(10)

(11)

(12)

当算法逐渐收敛时，由于群体中个体的适应度值比较接近，造成寻优停留在最优解附近，为提高选择能力，此时应增大个体适应度值。因此针对式(11)的适应度函数进行重新标定，即：

(13)

式中：F(t)为标定后的适应度值；Fit(t)min为原适应度函数值的下界；Fit(t)max为原适应度函数值的上界；δ为开区间(0，1)内的一个正实数。

4)选择与交叉。

(14)

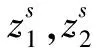
5)变异。

在寻优过程进入后期时，由于采用的标准遗传算法其变异概率保持不变，使得算法在后期迭代时停滞不前，降低了收敛速度。为加强局部搜索能力，在后期引入新的变异算子。具体定义如下：

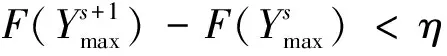
4 仿真实验

4.1 构建机器人模型

首先对PUMA560机器人进行运动学分析，采用D-H法建模，构建机器人各关节坐标系，并求出对应参数，即关节角θi、相邻两关节轴扭角αi-1、连杆长度ai-1、相邻两连杆间偏置di，再将参数导出，具体见表1。

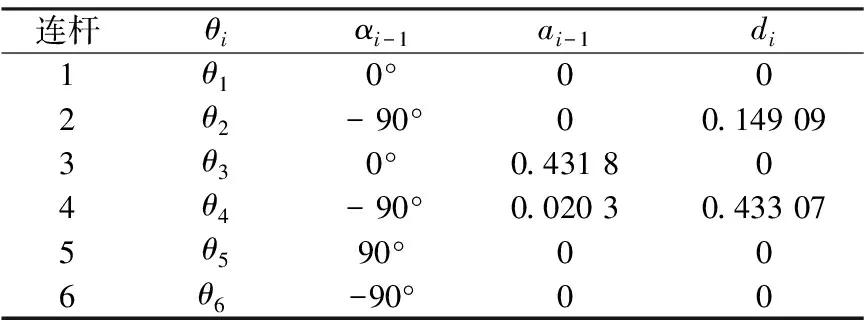
表1 PUMA560的D-H参数表

在MATLAB的Robotics Toolbox中创建PUMA560机器人，将D-H参数表中各数值导入Link函数LINK([alpha A theta D sigma offset],‘Standard’)中来定义连杆属性，再用SerialLink函数SerialLink([L1,L2,L3,L4,L5,L6])定义6个关节属性，建立的机器人模型如图2所示。

图2 PUMA560机器人模型

4.2 时间优化

本文引用文献[10]、[11]中的型值点参数和各关节运动学约束条件，其参数见表2和表3。对PUMA560的前3个关节(腰部、肩部、大臂)进行时间优化，对比上述文献中的结果，验证改进的遗传算法的可行性。

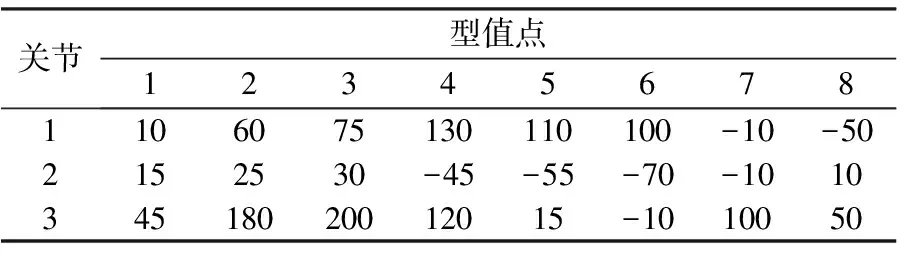
表2 型值点关节位置序列 (°)

总共选取8个型值点，并且3个关节运动轨迹的起点与终点角速度都为0。

表3 运动学约束条件

将型值点的关节位置序列代入改进后的遗传算法进行优化仿真，在满足关节的角速度、角加速度、角加加速度的约束条件下，求解的前3个关节的最优轨迹规划时间为[14.015,14.317,13.952]s，比文献[10]中的优化结果[20.680,20.772,19.920]s减少了[6.665,6.455,5.968]s,比文献[11]中的优化结果[16.018,16.444,17.416]s减少了[2.003,2.127,3.464]s,达到了对机器人轨迹规划运行时间优化的目的。将优化后的时间迭代图与文献[7]、[11]中的AGA(自适应遗算法)、SGA(标准遗传算法)的迭代图进行比较，其对比结果如图3所示。

图3 算法迭代收敛对比图

由图可知，采用SGA算法在第180代时开始收敛，采用AGA算法在第90代时开始收敛，而基于聚类方法的遗传算法在第75代时就开始收敛，收敛速度得到较大提升，说明该算法在后期的搜索效率得到提高，缩短了算法迭代收敛的时间。进行时间优化后的关节角位移、角速度、角加速度与角加加速度的曲线如图4所示。由图可知，优化后的角位移、角速度、角加速度的运行轨迹连续且光滑，同时满足表3中的运动学约束条件，完成了机器人时间最优轨迹规划的任务。

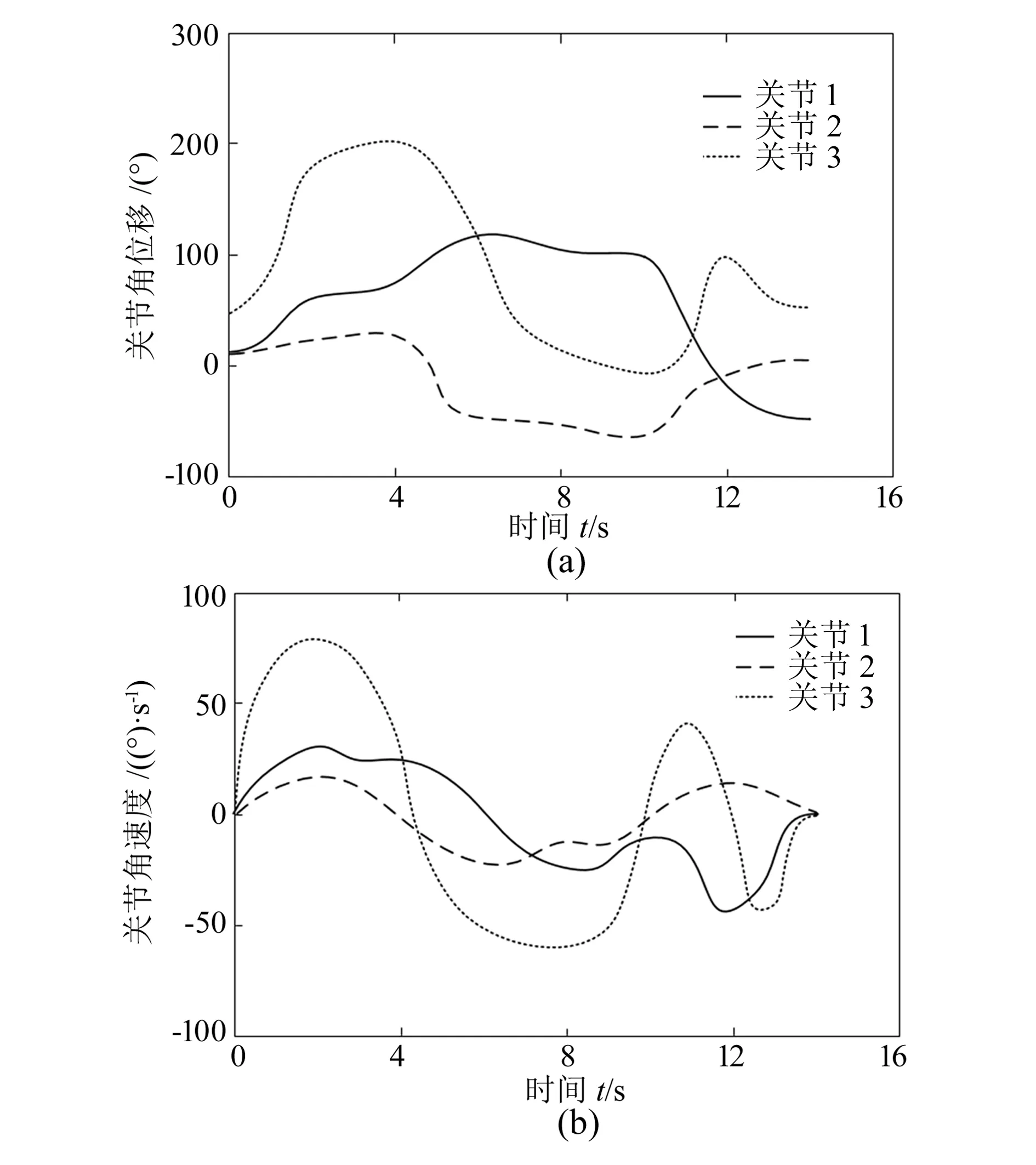
图4 关节时间最优轨迹曲线

5 结束语

本文利用三次样条函数拟合机器人运动轨迹，保证各关节角位移、角速度、角加速度的连续性。在满足运动学约束条件的情况下，利用基于聚类方法的遗传算法对插值时间进行优化。从对比实验的结果来看，该算法在后期的迭代收敛速度得到提升，机器人各关节的运行时间也明显缩短。在后期的研究中，将对能量、冲击等目标进行综合优化，以进一步提高机器人运行效率。