改进的SURF特征提取与匹配算法

张晓宇，何文思，段红燕，魏松涛

(兰州理工大学机电工程学院，甘肃 兰州 730050)

在机器视觉研究领域，图像匹配一直是其中重要的组成部分。匹配算法根据其思想可以分为两大类：基于区域匹配方法和基于特征匹配方法，其中基于特征的匹配方法有计算速度快、鲁棒性好和对图像变形不敏感等优点，是常用的匹配方法。

SIFT(scale-invariant feature transform)[1]是最常用的特征点检测算法，对图片的平移、缩放、旋转等具有不变特性，然而SIFT算法在计算特征点描述子的时候对每个特征点都需要构建128维特征向量，这样就降低了运算速度。Wang和Bay等[2-3]提出的SURF(speeded up robust features)算法，继承了SIFT的不变性，并在提取图像的特征点运算速度上比SIFT快3倍左右[4]。然而SURF算法在求取特征点主方向时受到局部区域像素梯度方向的影响，在匹配过程中仅使用欧氏距离作为评判标准，使得匹配产生较大误差。本文提出一种改进SURF算法，先利用余弦相似度进行二次匹配来去除伪特征点，再使用随机抽样一致算法(random sample consensus，RANSAC)进一步降低误匹配率。

1 SURF算法原理

SURF是一种具有高效性和高鲁棒性的局部特征描述算法，其不仅对图像旋转、缩放具有极强的适应性，而且图像环境在光照变化、视角变化、仿射变换和噪声的情况下也能保持一定程度的稳定性[5]。SURF特征匹配算法可以分为3个步骤：特征点检测、构建特征描述子和特征点匹配[6]。

1.1 特征点检测

特征点检测可分为3步：尺度空间极值点检测、精确定位极值点、选取特征点主方向。

1.1.1 尺度空间极值点检测

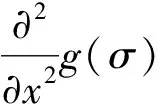
(1)

由于图像中的特征点需要具备尺度无关性，所以先对特征点进行高斯滤波消除特征点的相关性，再进行Hessian的计算。L(x，t)代表不同解析度下的图像，计算公式如式(2)、(3)所示。

L(x,t)=G(t)·I(x,t)

(2)

(3)

式中：I(x,t)为图像函数。

Herbert Bay提出用近似值代替L(x,t)以达到简化计算的目的，同时引入权值带消除误差，权值大小会随尺度变化而发生改变，则Hessian矩阵行列式为：

det(Happrox)=LxxLyy-(0.9Lxy)2

(4)

式中：det(Happrox)为像素点的Hessian矩阵行列式；Lxx,Lyy,Lxy为高斯滤波后图像在各个方向的二阶导数。

匹配图像具有不同的空间尺度，图像金字塔可以将模板图像求解出多种尺度空间以适应匹配要求。传统的金字塔结构各层待检测图片尺寸大小发生了变化，各子层在运算过程中都需要用高斯函数进行平滑处理，降低了运算效率，如图1所示。但在SURF算法中，各个octave层之间的待检测图片尺寸大小是相同的，只改变了滤波器大小。采用这种方法缩短了采样过程所消耗的时间，处理速度得到较大提高。

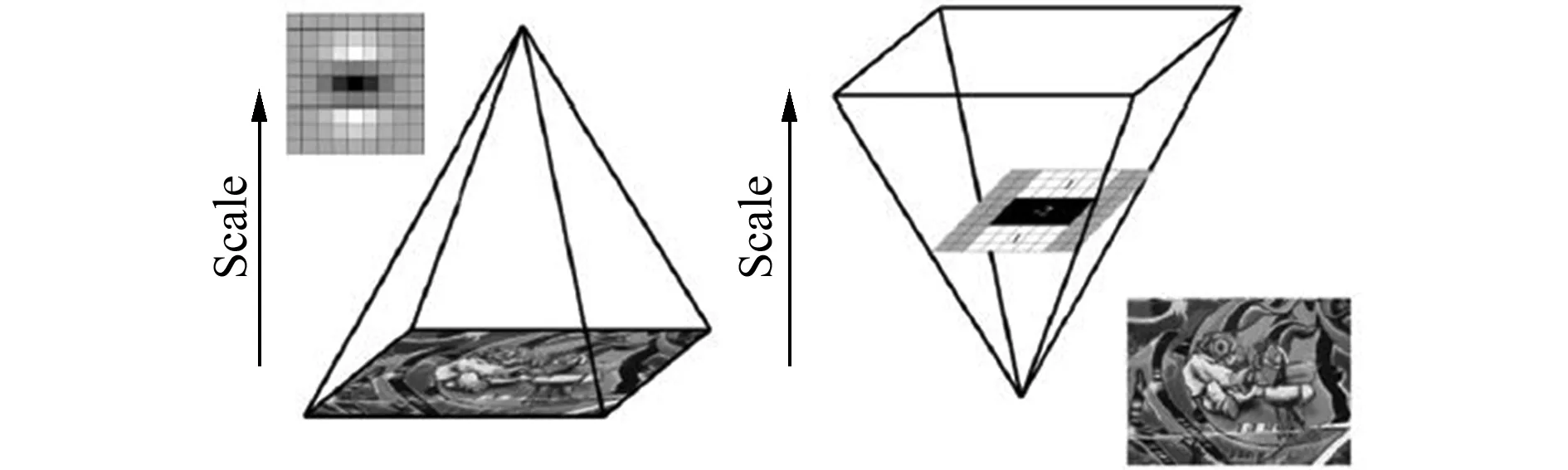
图1 金字塔结构

1.1.2 精确定位极值点

将Hessian矩阵处理过的每个像素点与其三维领域的26个点进行对比，如果是极值点则保留，反之剔除，再通过三维线性差值法获得亚像素级的特征点，并删除检测特征点中小于一定阈值的点。

1.1.3 选取特征点主方向

在特征点区域内统计其haar小波特征，以60°扇形为单位，统计扇形区域内所有特征点的水平和垂直haar小波特征总和，然后60°扇形以一定间隔进行旋转，旋转一周后以小波特征最大的扇形方向作为该特征点的主方向，过程示意图如图2所示。

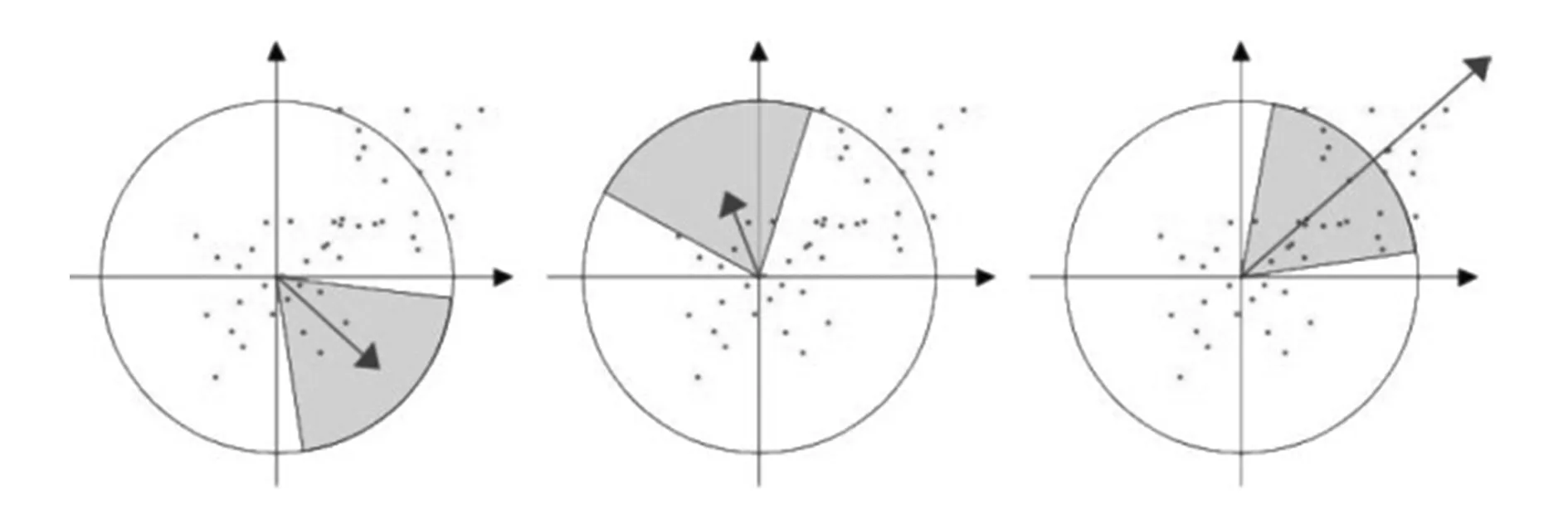
图2 特征点主方向求取过程

1.2 生成特征描述子

在特征点周围选取一个正方形框，边长为20s(s为该特征点的尺度)，方向为特征点的主方向，然后把该框分成16个子区域，每个子区域统计25个像素的水平和垂直方向的haar小波特征，从而形成四维向量V=[∑dx∑|dx| ∑dy∑|dy|]，归一化后形成16×4共64维SURF描述算子[8]。其中dx为水平方向haar小波特征；dy为垂直方向haar小波特征；|dx|为水平方向haar小波特征的绝对值；|dy|为垂直方向haar小波特征的绝对值。

1.3 特征点匹配

特征点匹配就是把两幅图像中特征点一一对应，然后计算第一幅图像的每一个特征描述子向量与第二幅图像的特征描述子向量的欧氏距离，计算所得的最小值即认为是那个特征的最佳匹配。

2 匹配算法的改进

SURF算法匹配过程中，如果匹配图像局部点领域信息相近和图像视角不同，会引起两个不同特征点描述符的匹配程度超过同一点的特征描述符匹配程度。因此在匹配的两幅图像中如果出现形状相似区域，就会产生大量误匹配。由于欧氏距离没有考虑各特征描述子向量之间的相关性，本文进行二次匹配，对误匹配对进行消除。

2.1 向量空间余弦相似度匹配

判断两个向量相似程度的准则一般有两种：距离测度法和相似性函数法。距离测度法是根据向量空间上存在的距离来判断向量间的差异程度。相似性函数是用函数值的大小来表明两向量间的差异程度。本文在欧式距离测度的基础上再用余弦相似度作为约束，通过设定相似性函数的阈值来去除多余的匹配点对。

余弦相似度测度，即计算特征点间的相似程度，将向量根据坐标值绘制到向量空间中，求得它们的夹角，并计算出夹角所对应的余弦值，此余弦值就可以用来表征两个特征点向量的相似性。余弦值越大，说明两特征点向量之间的夹角越小，匹配相似度越大。

具体方法：先使用欧氏距离选取初步特征点对，然后再使用余弦相似度函数进一步筛选，如果两个向量的余弦值大于阈值K则保留，反之删除。K可以根据实验得到，对于2个向量a和b，余弦相似度S(a,b)表达式为:

(5)

使用余弦相似度对产生缩放和旋转、亮度对比度改变、模糊、视角变化的4类图像进行测试，选择平均阈值K=0.975，测试结果见表1。

表1 测试结果

2.2 改进的RANSAC算法

RANSAC算法设立一个阈值把测量数据分为内点和外点，其中内点数据比较准确，因此利用内点数据进行参数估计，以便删除不准确的数据。此算法需要事先确定3个量[9]：随机采样次数、误差容忍度(内外点距离阈值)和一致集的大小(内点总数)。

在经典的RANSAC算法中，计算最佳模型参数是遍历所有可能的组合，并以误差最小的一组作为最佳参数，往往导致计算量大、运行时间长。本文采用PROSAC(the progressive sample consensus)将余弦相似度匹配的结果作为排序的依据，在采样时根据匹配结果由高到低进行排序，如此最有可能导致最佳参数的采样会较早出现，从而减少随机采样次数、提高运算效率。

3 实验结果与分析

用于实验的硬件为联想ThinkPad E420，其CPU主频为2.2GHz，内存4GB；程序在Visual Studio 2010开发环境下编写。测试用图为经典测试图像，以正确匹配率作为评价标准[11]。

(6)

式中：precision为正确率；falsematches为错误匹配；correctmatches为正确匹配。

使用原SURF算法和改进SURF算法分别处理测试图像，如图3～6所示，其中(a)为使用SURF算法匹配效果图，(b)为改进SURF匹配效果图。图3为旋转45°、尺度增加2倍，图4为经过模糊变化，图5为亮度有较大改变，图6为相机视角发生变化的。表2是实验数据。

图3 匹配旋转和缩小图像

图4 匹配模糊变化图像

图5 匹配亮度变化图片

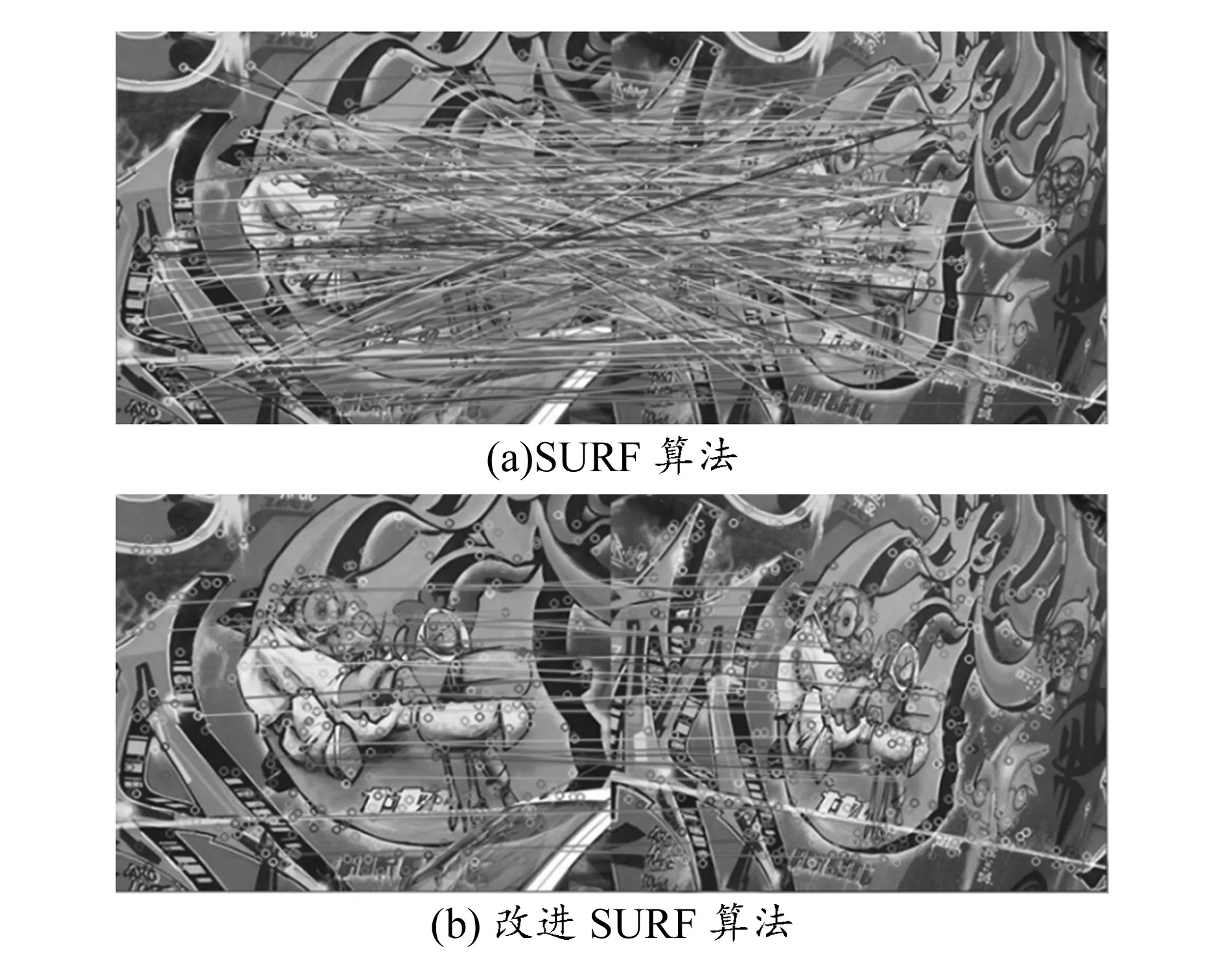
图6 匹配视角变化的图片

图像处理方式算法左图特征点数量右图特征点数量匹配点数量正确匹配点数量正确率/%时间/s旋转和缩放SURF61441061437360.751.13改进SURF448224313096.771.31模糊SURF1681011689657.141.02改进SURF131621919100.001.24亮度SURF127881277861.411.14改进SURF105664242100.001.36视角SURF32732232720863.611.21改进SURF225230171694.111.32

从表2可知，改进SURF算法与原SURF算法相比，改进算法在不同条件下的图像匹配正确率都有显著提高，误匹配率平均降低37%，匹配时间比SURF算法增加0.1～0.2s。使用余弦相似度进行二次匹配，需要选取的特征点平均减少20%～30%，说明本文算法稳定可靠，对图像产生旋转、缩放、模糊、亮度和视角变化等情况都有较强的适应性。

使用SURF和本文算法对随机拍摄的一幅照片进行匹配，余弦相似度阈值K=0.975，人工对匹配结果进行校验，发现误匹配对为0对，匹配正确率为100.00%，所用时间比SURF多0.12s，在可接受的范围之内，如图7所示。

图7 匹配实验图片

4 结束语

本文在用SURF算法提取特征点的基础上结合余弦相似度进行进一步提取，很好地解决了SURF算法匹配中没有考虑特征点空间位置关系从而导致误匹配率高的问题。本文提出的方法可以在保证正确率的基础上对图像的旋转、缩放、模糊、亮度变化和视角变化具有较强的鲁棒性，匹配正确率较高。但是由于旋转和视角变化易使相近特征点方向一致，导致余弦相似度进行二次匹配对误匹配点去除不完全，还需要做进一步的研究。