数控机床主轴振动信号监测及提取方法优化研究

苏 健，汪木兰，朱晓春，丁文政

(南京工程学院江苏省先进数控技术重点实验室，江苏 南京 211167)

数控机床在我国已实现量的普及，随着中国制造2025时代来临，机床已经向高、精、尖方向发展。为充分收集机床各方面运行数据，了解运行状态，急需提升监控数据的精度，这也体现了当前时代的迅速发展和急切的社会需求。预测和健康管理(prognostic and health management)是美国军方基于视情维修提出的新的设备维护策略，保证了军方具有设备故障诊断和健康管理的能力[1]。在众多故障源中，振动引起的零部件损坏是机床故障的主要原因之一。因此本文以机床运行振动信号监测及数据优化研究为背景，构建机床主轴监测优化系统。采集运行过程中的数据信号，通过理论模态时频域分析，计算出最优参数，以提升整个机床的监控数据精度，及时预测机床故障情况，将机床的生产率和生产成本控制在最优。

在测量主轴振幅电信号的实际工程环境中，传感器采集的振动信号不仅含有大量噪声，还包括直流分量和各种异频成分。因此如何从混合信号中准确提取基频振动信号幅值一直是该领域的研究热点[2]。快速傅立叶变换(fast Fourier transform，FFT)不但能减少频谱外漏，而且可以提升异步采样测量值的精度。但在截取信号过程中，会存在栅栏效应，即采样频率不等于基波频率的整数倍[3]。为此很多学者提出了不同的处理方法,王刘旺等[4]采用加汉宁窗差值法；蔡晓峰等[5]运用加窗三谱线插值FFT算法的原理，提出一种改进三谱线插值修正算法；曾博等[6]提出基于Nuttall自卷积窗的改进 FFT 谱分析方法。为提升信号处理过程中幅值的准确性，本文提出了基于FFT算法的三次样条函数的改进算法，并结合递推平均滤波法优化提取时域和相位。实验硬件部分由压电传感器、多功能调理电路放大器、动态信号分析仪、计算机组成。软件部分利用设置模块对采集数据形成有效的优化分析，输出时频域并储存在处理器。

1 采集系统算法基本原理

1.1 基于三次样条函数的FFT算法

FFT算法是DFT(discrete Fourier transform)算法中的一种高速算法[7]。在算法上进行改进，得出按时间和频率抽取的两种算法。

设x(m)为G点的有限长序列，即在0≤m≤G-1内有值，则定义x(m)的N点离散傅立叶变换变化为：

(1)

(2)

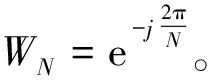
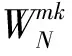
常见的数值逼近拟合方式有线性插值、埃尔米特插值、最小二乘插值、样条插值等[8]。三次样条插值函数中包含了由三次多项数表达的分段函数，且此分段函数是光滑、连续、可导的，保证了多阶导数的可导性和连续性。分段函数中包括了由于数据泄漏而没有采集到的分段点，在提高采样精度的同时也保证了数据的稳定性和可靠性。

在实验过程中分别采集了x个时间分段点(ti,pi),i=0,1,…,n。其中ti为采样时间，pi为采样值。设二阶导数φ″(ti)=Mi，其满足[ti,ti+1]区间内的三项函数关系，故φ″(ti)可设为线性函数：

(3)

式中：∂i=ti+1-ti,为插值基函数。

对φ″(t)进行两次积分变换，利用插值条件φ(ti)=pi，φ(ti+1)=pi+1可以得到：

(4)

式中：i=0,1,…,n-1。

通过对φ(t)求导得到Mi，结合式(2)、(3)得：

(5)

(6)

同理可得：

(7)

根据φ′(ti+0)=φ′(ti-0)得：

μiMi-1+2Mi+λiMi+1=di,i=1,2,…,n-1

(8)

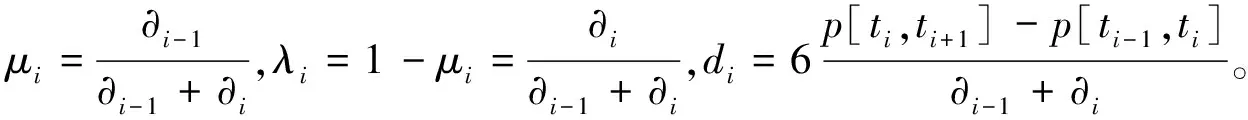
将式(8)写成矩阵形式为：

(9)

(10)

因方程组(9)的系数矩阵是严格对角占优矩阵，结合式(10)容易求得函数Mi。

1.2 振动信号的均值处理

在机床所处环境和生产过程中，包含着大量噪声信号，需要滤去无用的高频段，保留所需低频段，即对原本杂乱无章的随机信号进行抑噪处理，一般可以通过均值函数时域平均算法实现。简单来说，均值函数是指离散傅立叶函数的周期均值，离散傅立叶函数是时域和频域的双域函数，即只需求出时域上的值，对应的频域的值是相同的。以时域平均算法选取拟合后的N段频率周期，将这N段周期依次叠加，求出最大幅值，在一定的时间范围内，就能体现出优良的去噪效果和良好的信噪比。离散傅立叶函数的均值函数定义式为：

(11)

各段信号频率在区间[0,ε-1]进行叠加可得：

(12)

再通过式(11)得到均值函数：

(13)

式中：Yi(τ)为周期信号中需保留的真实信号；Ni(τ)为信号中的噪声信号。

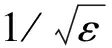
(14)

式中:y(s)为滤波器输出；f(γ)为滤波器输入；s0为滑动滤波长度。

1.3 振动信号的提取

一般情况下振动信号s(t)的提取公式为：

(15)

式中:α0为直流分流；α1为基频信号幅值；φ1为基频信号相位；αi为异频信号幅值；ωi为各信号频率；φi为异频信号相位；n(t)为各种干扰信号。

设振动信号的基频为ω1，则参考信号为：

(16)

首先将s(t)与y(t)相乘得：

(17)

然后将s(t)与z(t)相乘得：

(18)

式(17)、(18)计算结果中包含直流分量中所需的有效信息，需设置低通滤波器的低频波段，将其他干扰信号滤去，然后再次与参考信号相乘，通过加法器求出基频不平衡信号，得：

s(t)=α1sin(ω1t)cosφ1+α1cos(ω1t)sinφ1=α1sin(ω1t+φ1)

(19)

最后结合三次样条函数的FFT算法，提取出基频振动信号的频谱特性。

2 仿真系统

2.1 测试系统组成

根据机床振动测试系统原理和现有实验室器材，利用数字信号传输技术、PC虚拟仿真技术构建振动测试仿真实验平台。平台包括压电传感器、信号调理放大器、Agilent35670A动态信号分析仪和计算机。振动信号采集测试流程如图1所示。

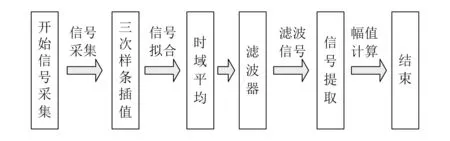
图1 振动信号采集测试流程

利用LabVIEW软件强大的动态数据处理能力，模拟现场硬件处理模块，一定程度上弥补了硬件的不足，此功能满足了实验的基本要求并保证实验的正常进行。振动测试系统整体框图如图2所示。

图2 振动测试系统整体框图

该系统的程序是基于 LabVIEW软件编写的，从信号采集程序和信号分析两方面入手，将多路信号同时输入该 LabVIEW 程序中，保证了数据的及时性和准确性，满足了同时采集多组振动信号的要求，是准确提取基频振动信号幅值的重要保证。信号采集程序显示模块为主轴测试系统设计的主要软件模块，其数据采集、分析、处理同时进行，体现出了软件强大的处理能力。

通过采集模块和分析模块，用LabVIEW程序中DAQ助手实现数据的连续采集。采集的数据通过不同的通道和配置参数补充信号密度并减小信号采集过程中的误差。再用单频测量方法实现主轴转速测量，以采集不同转速情况下主轴振动的情况。通过编写基频提取程序处理采集信号，将位移值和转频测量结果输入到两个Basic模块中，得到时域、频域分析中关键的幅值和相位值。通过正、余弦定理构造基频信号，频域图中满足要求的幅值能直观清晰地显示在图表中，且更为简捷、方便和高效。转速测量程序如图3所示。

提取基频信号幅值程序如图 4所示。

2.2 仿真计算及分析

通过LabVIEW的虚拟仿真功能可使设计程序正常运行，将采集到的原始振动信号以正、余弦信号形式表达出来。在采集过程中会有各种环境噪声，其波形差异巨大。主轴振动信号会受到多种随机噪声的干扰，其中高斯白噪声是随机噪声中最主要的成分[10-11]。

图3 转速测量程序

在采集过程中根据采样定理设定采样频率，采样频率过高或过低都会对采样信号造成影响。过高会使计算机计算量增加，负载过高，造成响应延迟；过低会增大原始信号恢复过程中的误差值，影响精度。因此，设置程序中采样率和采样点数均为2 048。

图4 提取基频信号幅值程序

为了保证不同情况、不同转速下采样信号的稳定性，设置了不同转速以及不同频率下的参数值，见表1。

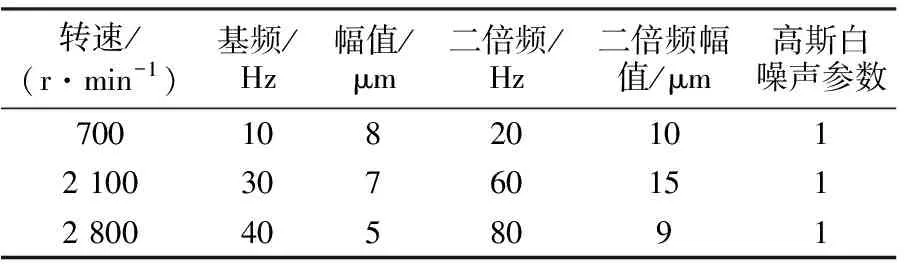
表1 参数设置

图5和图6显示的是采集到的原始振动信号。其波形无规律可循，幅值虽能控制在一定范围内，但在特定时间段内无法形成稳定的周期波形，进行傅立叶变换前的频谱含有多个频率峰值，此外所需振动信号没有有效地体现，存在不同程度失真，无法求得相应幅值和相位。故对信号进行提取处理后，图7和图8中信号波便能以正弦形式有效显示，且具有良好的平滑度和规律性。幅值有良好的平滑度，符合基频振动信号的特征并保证求出高效基频频率。

本文所用改进三次样条函数算法与分析仪运用的相关算法得出的数据见表2。由表可知，本文算法的幅值误差精确度明显较高，达到32%以上，且在一定程度上能保持较好的稳定性和实时性，在保证数据正确性的前提下满足了幅值提取精度的基本要求。

图5 振动信号波形图

图6 振动信号频谱图

图7 处理信号波形

图8 处理信号频谱图

表2 运算结果对比

3 结束语

数控机床主轴振动幅值算法精度的提升是机床健康状态监测数据准确性的重要保障。对机床信息状态进行反馈、汇总并分析，能及时预测机床可能出现的状况，将问题准确地显示在人机交互界面并报警，帮助操控人员面对不同情况采取不同的处理方式。这种高效预测、处理机床问题的技术方法对于企业实际运营成本的降低具有重要作用，从细节方面减少了机床诊断、维修的时间，延长了使用寿命，保证了机床的生产效率，提升了整个企业的利润率，体现了所具有的应用价值与潜力，拥有巨大的行业前景。