高精度机械零件外观三维设计

崔 畅，刘 萍

(西安工业大学艺术与传媒学院，陕西 西安 710032)

机械零件是构成机械的基本元件。随着机械制造业的飞速发展，如何才能制造出高精度的机械零件已成为人们研究的重点，其中机械零件的外观设计是体现零件精度高低的一个重要因素[1-2]。但在实际生产过程中，厂商往往容易忽略对高精度机械零件的外观进行精心设计，导致许多机械零件在外观设计方面无法满足客户的需求。三维设计技术广泛应用于多个领域，可实现多专业的协同设计理念，已成为一种常用的机械零件设计技术。相关专家学者以机械零件外观为对象进行了深入研究，已取得了一些成果[3]。文献[4]首先对零件图像的边界信息进行提取，并给出了零件尺寸计算方法，然后通过构建零件外观图像，对复杂机械零件的外观设计尺寸进行检测，实验结果表明，复杂机械零件的外观尺寸检测性能较好，但零件外观的尺寸比例控制效果较差，需要不断调整，从而导致设计周期较长；文献[5]主要研究采用AutoCAD软件设计的机械零件三维图，具体研究过程中，选取方形体和旋转体机械零件为研究主体，分别对两种零件的几何结构特征进行分析，根据各自特点选取最优的外观设计方法，该方法存在零件轮廓点位置计算不准确的问题；文献[6]以Visual Basic为编程语言，依据零部件结构参数表对各参数进行匹配、调节，完成主要零件的三维参数设计，该方法存在设计周期较长的问题。针对上述存在的问题，笔者提出一种新型高精度机械零件外观三维设计方法，通过构建机械零件外观结构的三维模型，实现零件外观设计。

1 高精度机械零件外观结构面动力学分析

在机械零件最初设计前准备阶段，需要收集并处理相关材料，正确预计机械零件在设计过程中将要利用到的性能因素。高精度机械零件多用于精密仪器设备，因此必须具备较高的动刚度。动刚度是机械零件设计成功与否的一个重要影响因素，对于研究与解决机械零件动态设计问题是极为重要的[7]。正确的动力性能分析是进行机械零件外观设计的关键，可有效提高机械零件外观结构优化程度并缩短设计周期。本节主要针对高精度机械零件外观结构的动力学特性进行分析，即首先在分析机械零件外观结构特点的基础上，构建外观结构面动力学模型，完成动力学分析。

将机械零件外观结构看作是一个多自由度系统，对这个多自由度系统进行研究的过程中会产生一种固有振动，需要明确的是，这种状态下的振动不是真实意义上的振动，其表示的是系统在无外力干扰的情况下，可能产生的一种静态的振动集合。当系统处于某一固有振动状态时，在任何时刻各自由度的位移之比是保持不变的[8-9]。通常情况下多自由度系统应该满足无阻尼自由度振动方程：

(A-λB)ω=0

(1)

式中：A为动力变量；B为外观结构变量；λ为外观结构特征值；ω为外观结构特征系数。使式(1)获得非零解的充分必要条件是非系数行列式的值为零，即：

|A-λB|=0

(2)

根据式(2)可获得机械零件外观结构特征值λ。在获取特征值的基础上，即可对机械零件外观结构的动力学特性进行分析。

对高精度机械零件进行动力学特性分析时，通常会用到有限元分析技术，即将一个无穷多自由度的系统进行离散化，转化成为类似于多自由度的系统，以便于研究[10-11]。机械零件的外观结构有限元分析模型如图1所示。

图1 零件外观结构有限元分析模型

根据图1所示的零件外观结构有限元分析模型，建立机械零件外观结构面的动力学模型，具体步骤如下：首先选用合适的单元类型与机械零件外观结构各组成面进行匹配，依据各自匹配得到的单元类型，建立其单元的动力变量、外观结构变量矩阵，然后将所有单元矩阵组合起来得到零件的动力变量、外观结构变量矩阵，从而构建该零件外观结构的动力学模型[12-13]。

假设u为零件外观结构面的节点位移量集合，u={u1,u2,u3,…,un}，其中n为零件上的节点总数；u1，u2，…，u6分别为节点在坐标系X，Y，Z以及θx，θy，θz6个方向上的位移。由此可以得到节点所受的外载荷向量f(t)：

f(t)=λ{f(t1)T,f(t2)T,f(t3)T,…,f(tn)T}

(3)

若节点处无外力作用，则f(t)=0。

假设动力变量矩阵A和外观结构变量矩阵B均为n×n阶对称矩阵，则：

f(t)=AB(θx+θy+θz)

(4)

根据式(4)可得出高精度机械零件外观结构的动力学模型W：

W=f(t)+u(A+B)

(5)

2 高精度机械零件外观三维结构设计模型

以前文中的零件外观结构动力学分析为基础，对零件结构的内外轮廓点进行计算，即可完成零件外观三维模型的设计。

在从中性面模型转换成实体模型的过程中，最重要的步骤是要确定外观结构面轮廓点的位置，通常情况下，会首先确定法向量位置，以此完成各个轮廓点的位置计算，图2所示即为实体图中的法向量。

图2 机械零件实体图法向量

现有的利用法向量确定轮廓点的方法得到的结果虽然是正确的，但当高精度机械零件外观为“Z字形”、“凸字形”等不规则结构的情况下，就无法利用法向量来确定整块板的轮廓点[14-15]。

本文在现有法向量确定方法的基础上进行改进，采用浮动法向量确定轮廓点。实际设计中，每一块板上面的法向量都是不一样的，且同一块板上面拥有无数个点，针对每一个点的法向量也是不同的，即板的基准向量不是固定不变的。机械零件外观结构轮廓点确定的具体步骤：首先选取板上第一个点的法向量作为基准向量，然后以基准向量为依据，对其他点的法向量进行调整，同时内外轮廓点也会随之变化，最终确定轮廓点位置。如图3所示，选取点1作为基准向量，从图中可以看出，点2,3,4的法向量与基准向量不一致，需要进行调整，相对应的内外轮廓点也会随之调整，从而生成两个侧面的轮廓。

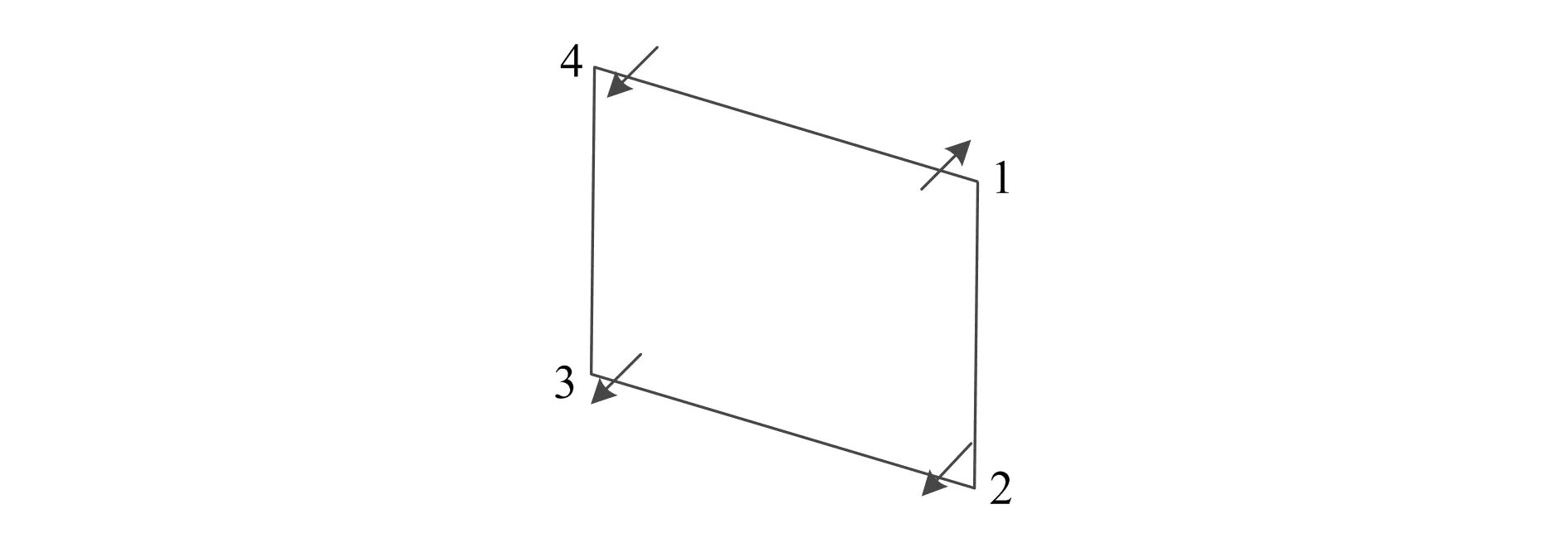
图3 机械零件外观结构点向量

计算出所有的轮廓点后，即可得到零件外观结构三维模型，从而实现了高精度机械零件外观的三维设计。具体流程图如图4所示。

3 实验测试与分析

为验证本文高精度机械零件外观三维设计模型的有效性，进行了仿真实验。首先在OMNet ++平台上建立高精度机械零件外观三维设计模型，然后利用仿真工具MATLAB 7对高精度机械零件外观三维设计模型进行测试。实验参数见表1。

图4 机械零件外观结构三维模型设计流程

表1 实验参数设置

在上述实验环境和参数设置条件下，利用本文模型模拟得到的高精度机械零件三维结构如图5所示。

图5 高精度机械零件三维结构

以图5中的机械零件为参照对象，选取设计周期为指标，对本文机械零件外观三维设计方法、文献[5]设计方法以及文献[6]设计方法进行对比，结果如图6所示。

根据图6可知，随着零件数量的增加，本文方法的设计周期延长速度较慢，且整体设计周期较短。而文献[5]和文献[6]的设计周期上升速度较快，整体设计周期较长。由此可知，本文方法设计效率较高，能够快速完成高精度机械零件的设计。

图6 不同方法零件设计周期对比图

为进一步验证本文提出的高精度机械零件三维设计方法的可靠性，以机械零件内外轮廓点位置计算值与实际值拟合程度为依据，对本文方法与文献[5]方法进行对比，结果如图7所示。

图7 不同方法轮廓点位置计算值与实际值的拟合程度

根据图7可知，用本文方法计算得到的轮廓点位置与实际值的拟合程度更高，表明本文设计得到的机械零件外观结构更加符合实际机械制造的需求。造成该结果的主要原因：本文在现有法向量确定方法的基础上进行改进，采用浮动法向量，选取板上第一个点的法向量作为基准向量，以基准向量为依据，不断对法向量进行调整，轮廓点位置也随之发生调整，最终得到的位置更加接近实际位置。

4 结束语

本文通过对现有方法进行改进，完成机械零件外观的三维设计，设计周期较短，设计效率高。但不同种类的机械零件具备不同特征，导致研究结果存在一定的局限性，因而后续工作将尽可能考虑不同种类机械零件的特征，以进一步完善零件设计方法。