舰机多设备组合搜潜方案决策方法研究

张雨杭,鞠建波,范赵鹏

(海军航空大学,山东烟台 264001)

随着潜艇在低噪高速技术方面的快速发展,常规的单设备搜潜作战已无法胜任复杂多变的战场环境,多设备组合协同搜潜成为当下海军发展建设的一个重要研究方向。对于多种设备组合使用的选择问题,执行搜潜任务中,若要保证搜潜的成功率,不能单凭指挥员个人进行方案决策,因此针对其建立有效的决策方法势在必行。

多属性决策问题广泛存在并适用于诸多领域[1],多属性决策往往只含有有限个预先指定的方案,决策的目的是要从含有多个指标的一组方案中,综合考虑各个指标,选出相比之下能最大限度满足实际要求的方案,经过半个世纪以来的发展,已产生贝叶斯理论、三角模糊数、云理论等较为常见这些方法,但单一使用其中一种进行决策,往往偏向主观或客观,影响决策效率与可信度。鉴于单一赋权法的缺点,兼并主客观的组合赋权方法正逐步应用各个领域[2],目前已产生如最大熵原理、区间估计、云模型等组合赋权方法,然而目前的方法大多只针对不同权重值之间的差异程度进行优化,使权重值趋向于均一化,弱化了各因素之间的差异,并不符合某些实际情况。本文提出了利用离差最大化法决策和理想点法组合赋权的相关知识,对水面舰艇和反潜直升机的多种搜潜设备间组合与选择问题进行决策,并通过实例来分析验证该方法的合理性与有效性。

1 搜潜方案决策模型建立

在进行设备选取决策前,首先要确立合适的搜潜设备方案集,并结合方案集确立评价其性能优劣的指标集。

1.1 确定设备组合方案集

水面舰艇与舰载反潜直升机通常配备多种搜潜装备,针对不同的战场战况条件及搜潜要求,通常可使用以下的一种或多种进行对潜搜索:各类声呐浮标(S)、吊放声呐(D)、拖曳声呐(T)中的,根据装备使用的实际情况,可以得到搜潜设备组合方案集:

U={u1,u2,u3,u4,u5}

其中,各方案的使用特点如下:

u1={S},声呐浮标单独搜潜,多采用被动浮标对位置分布较大的水下航行潜艇进行大面积隐蔽搜索;

u2={D},吊放声呐单独搜潜,一般对已知在搜索前某时刻大概位置或运动参数的水下航行潜艇按路径逐探点搜索;

u3={S,D},吊放声呐和声呐浮标联合执行搜潜任务,主要对水下航行状态的潜艇进行较高精度搜索;

u4={S,T},拖曳声呐和声呐浮标协同执行搜潜任务,一般用于对位置分布较大的水下航行潜艇进行大面积搜索;

u5={D,T},拖曳声呐和吊放声呐协同执行搜潜任务,一般对已知概率航向的水下航行潜艇进行大面积搜索。

1.2 确立评价因素指标集

将搜潜设备组合方案集确定后,结合考虑潜艇运动特点与航空反潜作战的需求,可从四个方面对设备组合方案进行评判,建立评价因素指标集如下:

P=(p1,p2,p3,p4)=

(搜索能力,隐蔽能力,可操作性,经济性)

在方案集U与指标集P的基础上,构建方案ui对指标pj的指标值记为rij,(i=1,2,…m;j=1,2,…,n),m与n为方案集元素与指标集元素的个数。

根据方案集U与指标集P的建立,可得对潜搜索效能方案评价指标结构如图1所示[3]。

2 基于理想点法的组合赋权法确定权重

2.1 利用权的最小平方法求取主观权重

权的最小平方法排序原理即权的最小平方法(WLSM)早由A.T.W.Chu等人与1979年提出,经华中理工大学陈珽教授在《决策分析》一书中首次对该方法进行介绍而引入我国[4]。该方法概念清晰,便于理解,对后来最优化排序理论和方法的发展起到了极大地引领和推进作用。在运用时一般将权的最小平方理论结合层次分析法归纳为以下步骤[5]:

1)确定因素指标权值的标度

引入1～9标度,将各指标进行比较,并构造量化判断矩阵。具体标度见表1。

表1 层次分析法指标权重标度

2)构造权重判断矩阵

根据表1各指标间相对重要程度与指标权重标度,可得权重判断矩阵

(1)

式中,aij表示指标i相对于j的相对权重。

3)计算指标权重

基于权的最小平方法的求最优问题可表示为:

(2)

其约束条件为:

(3)

则排序权向量即主观权重可表示为:

(4)

其中，

(5)

E=(1,1,…,1)T

(6)

2.2 利用改进的CRITIC法求取客观权重

CRITIC(Criteria Importance Though Intercrieria Correlation)法是由Diakoulaki于1995年提出的一种客观赋权方法,它是以特征的对比强度和特征的冲突性两方面来综合确定特征的客观权重[6]。该方法通常以标准差σj作为对比强度的表现形式,即σj越大,指标j下各方案所对应取值的差距越大,对比强度就越强。指标间的冲突性则与指标相关性相对立,若以rjk代表指标j与指标k之间的相关性,则特征的冲突性可表示为:

(7)

设指标j所包含的信息量为Ij,则有

Ij=σjCj

(8)

Ij越大表示指标j相对其他指标重要程度越高,根据Ij可得指标j的权重为:

(9)

在指标体系中,各指标的重要程度各有不同。通过给指标附加权重,能够提高指标间的差异程度,突出主次便于决策。传统CRITIC法考虑了指标的独立性与变化程度,优越性较显著,但仍存有不足之处,目前常用的改进方法有如下两点[7]:

1)标准差σj仅能反映单个指标的绝对变化程度,缺乏指标间的对比性,因此用差异系数代替标准差;

2)计算冲突性时,指标j与指标k间的相关系数rjk可能会出现负值,而复相关系数能综合反映一个变量与其他多个变量间的相关程度,且值分布在0到1之间,因此用复相关系数表示指标j与其他多个指标间的相关性更加妥当。

则由以上提出的两个问题,归纳改进的CRITIC法如下:

求取指标j的差异程度:

(10)

指标j与其他指标间的不相关性表示为:

Cj=1-Rj

(11)

其中,Rj为指标j与其他指标间的复相关系数,即n-1元线性回归模型pjk=β0+β1pj1+β2pj2+…+βkpj,k+…+βnpin+μj的决定系数R2的平方根。

指标j包含的信息量:

Ij=djCj

(12)

由此可得指标j的客观权重值为:

(13)

即得客观权重μ(μ1,μ2,…μn)。

2.3 利用理想点法求取组合权重

(14)

Di越小,则方案i与理想方案越接近。

为计算方便,对向量进行单位化,令

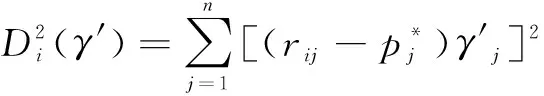
(15)

(16)

为兼顾主、客观权重,构造如式(17)的非线性模型求权重偏差的最小值

(17)

(18)

(19)

(20)

其中，T=(t1,t2,…tn)。

为求函数的极值,可构造式(21)的拉格朗日函数进行求解:

(21)

对上式求导,得

(22)

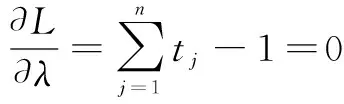
(23)

(24)

2KT+λ=KC

(25)

2KTE+λE=KCE
⟹2K+γE=2K
⟹λE=0
⟹2T=C

(26)

即得到

(27)

归一化处理可求得指标j的组合权重值:

(28)

即得组合权重ω(ω1,ω2,…ωn)。

3 利用离差最大化法决策与排序

3.1 评价指标分类与无量纲化处理

一般的多属性决策方法在处理评价问题时往往会出现评价结果相近、评价值之间差异较小、结果区分度不高等问题,不便于方案的排序和择优,而利用离差最大化的方法能够放大评价值之间的差异程度,以便于更好地区分各方案的优劣[9]。

在决策中,一般将各指标按指标要求分为以下四种类型,即效益型、成本型、固定型与区间型。效益型指标要求指标值越大越好,成本型指标要求指标值越大越好,固定型指标要求指标值取某固定值时为最佳,而区间型指标要求指标值在某区间内取值时为最佳[9]。在决策前往往要将各型指标无量纲化处理,不同的类型的评价指标有着各自的处理方法。设由原始数据rij无量纲化处理后得到zij,则对于效益型指标,有[9]

(29)

对于成本型指标,有:

(30)

对于固定型指标,有

(31)

对于区间型变量,有

(32)

式中，(a,b)是rij的理想变化区间。

3.2 确定评价值

易知0≤zij≤1,zij的赋值越大,说明该指标越接近最优水平。根据简单加权法(SAW),各决策方案ui的多指标综合评价值可表示为[10]:

(33)

qi(ω)越大表示决策方案ui越优,即可对方案进行排序或优选。

4 实例分析

4.1 获取各方案指标值

在四种评价因素中,搜索能力可根据各方案下组合设备的搜潜效能求得,其他指标可由专家给出的评判结果而得,由此可得各方案因素指标如表2所示。

表2 各方案下因素指标

4.2 获取权重

1)求取主观权重

首先根据表1的对比关系,得到权重判断矩阵,再由式(4)求得主观权重如表3所示。

即求得主观权重γ=(0.5174,0.2011,0.2011,0.0804)。

2)求取客观权重

为便于进行数学计算,将表1中的评判语言变量转化为评判标度,即对其进行数字化转换,二者对应关系如表4所示。

表3 权的最小平方法求取主观权重

表4 评判变量与评判标度对应关系

由表4对应关系可得转换后因素指标如表5所示。

表5 转换结果

根据式(10)、(11)、(12)、(13)可得客观权重及相关参数如表6。

表6 客观权重及相关参数

即求得客观权重μ=(0.6081,0.2051,0.1142,0.0726)。

3)求取组合权重

根据求得的主客观权重与式(27)、(28)求得组合权重及相关参数表7所示。

表7 组合权重及相关参数

即求得组合权重ω=(0.5560,0.2014,0.1662,0.0764)。

4.3 决策与分析

因素指标集中的四个指标均为效益型指标。则根据式(29)可得

再将z与求得的组合权重ω代入式(33),求得综合评价值:

q=(q1,q2,q3,q4,q5)=

(0.3676,0.6596,0.7149,0.6318,0.5183)

将上述值进行大小排序可得:

q3>q2>q4>q5>q1

由排序结果可直观体现:当对处于水下航行状态的潜艇执行搜潜任务时,方案u3最佳,方案u1则最差,即此时应优先选择方案u3中的设备组合进行对潜搜索。

在实际搜潜中,吊放声呐与声呐浮标协同搜潜,可有效提高搜潜概率,而声呐浮标单独搜潜概率较低,搜潜能力不佳。对于舰机协同下的两种搜潜方式,搜潜概率较高但经济性相对较差,且可行性受初始距潜距离限制。方案u3能兼顾搜潜能力与经济性,而方案u1多以被动方式工作,搜潜能力有限,搜潜概率最低。根据以上实际搜潜情况进行分析比对,验证了该决策方法的可行性。

5 结束语

本文在提出基于理想点法的组合赋权法与离差最大化决策理论的基础上,引入权的最小平方法与改进的CRITIC法求取主客观权重,来解决常规决策方法缺乏主观性、准确率不高的问题,并能够有效提高因素指标的区分度。一方面利用离差最大化法决策可快速直观体现方案的差距,另一方面利用组合赋权兼并主客观权重使结果更加综合准确,并通过实例分析进行了验证。该方法能直观快速地反应方案的优劣程度来加以决策,适用于舰机协同搜潜多设备组合决策问题,对于反潜作战具有一定的军事意义。