教学“解决问题的策略”之策略
2018-11-30王梦青
王梦青

【摘要】数学教学活动是一个复杂的知识与思维的交融过程。教师在这一活动中应着力于科学的知识呈现与相应的思维引领,要精选数学素材、强化基础训练、拓展问题情境,让学生在学习过程中自主生长,积极思考、细心分析、善于思维、主动建构、灵活运用策略解决相关问题。学会站在自己的角度独立分析、思考问题,逐步积累对数学问题分析的经验,形成终身的数学学习能力。
【关键词】教学活动 策略 思维
数学教学活动是一个复杂的知识与思维的交融过程。教师在这一活动中应着力于科学的知识呈现与相应的思维引领,学生的参与应凸显两个特点:一是发展与建构知识,二是在知识的建构活动中萌生思维序列、数学方法及解决相应问题的策略。而让教师为难的就是知识如何呈现、思维如何引导,由此派生出了教学研究、教学策略。教学策略科学与否,直接影响到学生的学习心理和参与程度。知识链接、思维选择、策略的合理建构,简单概括为课堂教学的质量与效率。只有教师教的策略与学生学的策略科学合理地融合,才能有效实现教学目标。
下面一道试题引发了我对“解决问题策略”教学的一些思考。
四年级数学期末测试卷中有这样一道解决实际问题的试题:
学生的解答不急于呈现。急于想要探讨的是学生的不同解答,警示教师的教学思想与课堂教学。“策略”怎样教学,该选择什么样的教学策略?笔者的实践感悟是:
一、精选数学素材,让学生感悟策略
学生对策略的感悟、理解与生成需要合适的素材情境,他们是在对相关素材的思考探究过程中发展思维,总结、归纳形成相应的策略,这是学生参与数学活动正向的学习过程,如果为了掌握策略而简单地揭示策略,视学生的模仿套用为掌握,则是教学的失误。不难看出,学生在数学学习活动中能否得到自主成长,取决于教师能否为学生提供自主成长的土壤。
以苏教版四年级下册教科书第48页例1为例:
观察线段图,大部分学生最容易想到的一种解法是把小春比小宁多的12枚去掉,这时小春就和小宁的邮票同样多,总数也跟着减少12枚,学生自然会想到数量关系是72-12=小宁邮票的2倍。这种解法是直观的,显性的。这道题,学生应该有三种不同的思维方式,教学中不能只满足于学生会解就可以了。另一种是隐形的,把小宁比小春少的12枚补上,这时小宁就和小春的邮票同样多,总数也跟着增加12枚,不难想到数量关系是72+12=小春邮票的2倍。第三种,用转化思想,将条件转化,把多的12枚的一半给小宁,这时两人变得同样多,数量关系是72÷2=小宁邮票枚数+6或72÷2=小春邮票枚数-6。
在教学活动中教师要优选相应的数学素材着力于学生思维发生、发展、形成过程的训练,将解决问题策略的教学过程,理解为启迪智慧、发展思维、自主建构策略的活动过程,将知识发生、发展的过程与学生学习活动科学地统一起来。
数学教学不是为了教会学生解决某些数学题,它应该是让学生在学习过程中自主生长,学会站在自己的角度独立地分析、思考问题,逐步积累自己对数学问题分析的经验,形成终身的数学学习能力。
二、强化基础训练,让学生理解策略
解决问题策略的教学是教学的重点,也是难点,教学时教师要根据学生的实际情况采用合理而可行的教学策略。应根据学生的思维特点,让他们的思维发展有一个循序渐进的过程。教师应为其做好相应的基础训练,让他们在解决相关的序列问题中发展思维、生成策略。
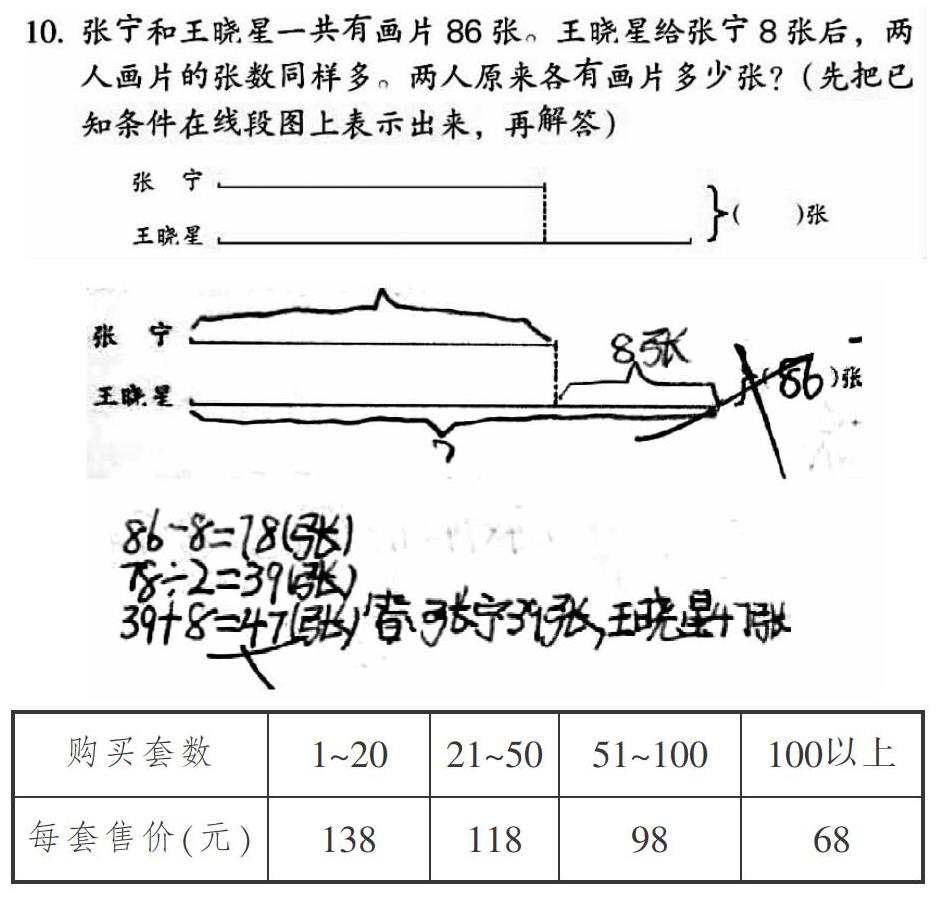
以苏教版四年级下册教科书第53页第10题为例:
这道题有多个思维层级,可以生成不同的解决问题策略,既可以直接给差数一半,实现同样多,也可以利用原有思维策略,去差、补差。
学生最喜欢选择他们认为熟悉的解题策略解答:
学生之所以会出现这样的错误,是因为这一习题与例题“差数”的呈现方式发生了变化,由显性变为隐性,需要学生经过思考分析,才能知道实际“差数”。教学时教师应作必要的思维铺垫。
教师可先引导学生正向认识差是多少,可设计这样两个题目:
1.小明和小华都有20本书,小明借给小华2本后,小华比小明多几本?
2.小明和小华共有20本书,小明给小华5本后,两人书的本数一样多,小明原来比小华多几本?
有关“差”的问题,不仅要正向把握,还应能灵活地反向理解。教师可设计这样两道训练题:
3.小红与小莉原来各有一些邮票,小红给小莉8张后,两人的张数一样多,小红原来比小莉多多少张?
4.小红与小莉原来各有一些邮票,小红给小莉4张后,小红还比小莉多1张,小红原来比小莉多多少张?
经过序列的思维训练,学生在数学“一一对应”的基础上理解了“差”的形成与变化,同时建立了找“差”的策略。无须多想,学生有了这些基础性思维能力后,他们在遇到新問题时就可能产生新的相应的解决新问题的策略。
由此,教师要将“认识”转化为“行动”。改“记忆数学”为“思维数学”,促进学生从浅表性学习到深层次学习,还数学学习的本真。
三、拓展问题情境,让学生自选策略
解决问题策略的教学不能仅仅着眼于学生会解题,而应重点关注学生是否能灵活地规划策略,选择相应的策略解决问题。这些能力的提升与发展都依赖教师的教学策略,课堂教学中是否提供科学合理又适合学生探究的素材与问题情境,相关的问题情境是否在不断地适合学生的思维发展的变化,教学活动中是否关注学生在解决问题时所选择策略的灵活性与合理性等众多的教学因素。正是这些隐性的因素推动了学生思维的发展和能力的提升。
现在我们再来看学生是如何解答本文开头呈现的四年级数学期末测试题。这道题不仅可以考查学生利用已有知识解决相关问题的能力,而且可以检测学生运用相关策略的实践能力,具有合理的区分度。
阅卷信息:关于试题的第二问,学生有如下几种不同的解答。
A:12+10=22(套),22×100=2200(元)。
B:12×120=1440(元),10×130=1300(元),1440+1300=2740(元)。12+10=22(套),22×100=2200(元),2740-2200=540(元)。
C:130×10=1300(元),100×10=1000(元),1300-1000=300(元)。
D:(120-100)×12=240,(130-100)×10=300,240十300=540(元)。
閱卷后对试卷评析,并与相关学生进行交流。
A:这道题和教材中第16题差不多。平时的练习,也都是合起来购买。
B:老师在讲解教材第37页第16题时,补充过这样的问题,如果合起来购买,可以节省多少元?
C:细读这道题,可以节省多少元,是省略了“四(2)班”,其实就是问“四(2)班可以节省多少钱”。
D:既然两班合起来达到优惠条件,就可按优惠条件分别计算,然后再合起来。
同样是类似的知识点,另一个学校的阶段检测卷中有这样一题:
新华书店进行《十万个为什么》新书发售推介活动,价格规定如下:
已知四(1)班有18名学生购买,四(2)班有54名学生购买,四(3)班有32人购买。
(1)每个班分别购买,共需要多少元?
(2)三个班合起来购买,共需要多少元?
据统计这道题的正确率高达98%。
对比这两道题的解答情况:后一题的得分率远远高于前一题。主要原因在于:后一题与例题相似,一看就知道怎样解答。只需要学生“识别—提取模型—重复应用已有的解题策略”。而前一题,问题发生了细微的变化,与平时训练的题型不完全吻合,需要学生“创造性运用已有的知识经验—重组新的认知结构、形成新的策略。同时我们也应看到,在同一个知识点上,部分学生只有模仿,没有策略。为此,教学中教师应依据学生实际采用合理的教学策略。
由此可见,拓展问题情境,有利于学生自选解决问题的策略。问题是引起思维的起因,不同的问题可能引发多维的思考策略,对学生的思维发展也具有不同的教学价值。学生用不同的策略解决问题,反映了他们的思维能力的不同层次,而他们选用的策略是否科学合理,又映射出他们思维的深刻性与逻辑性。因而教师提供的问题情境要多变,教学策略要多维。
综上所述,解决问题策略的教学要有合理的教学策略,要精选教学素材,在教学活动中引导学生积极思考、细心分析、善于思维、主动建构、灵活运用策略解决相关问题。让学生在积极参与学习活动的过程中充满自信、增强数学素养,提升数学教学活动的育人价值。
