面内变刚度功能梯度圆形薄板的轴对称弯曲

朱竑祯，王纬波，高存法，殷学文

（1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016；2.中国船舶科学研究中心 船舶振动噪声重点实验室，江苏 无锡214082）

0 引 言

船舶的振动噪声影响船舶结构的安全性、设备的灵敏性、船员的舒适性以及舰艇的隐声性能等。开展船舶板类结构的振动与噪声控制是一项十分重要的工作。随着舰艇低频噪声问题的日益突出，智能结构在船舶结构物中的应用与智能结构的主动控制研究，受到了各国的重视。美国最新型的海浪级核潜艇中装备了振动噪声主动控制系统与其全舰噪声监控系统配合使用，取得了良好的声隐身性能。波兰JERZY WICIAK对承受流体载荷力的水下结构的声辐射进行研究，对粘贴有压电作动器和传感器的圆形板的主动噪声控制进行了试验验证。美国麻省理工学院正在研制一种增强型主动降噪潜艇壳体模型，壳体周围粘贴有压电陶瓷。

功能梯度材料（Functionally graded material,FGM）作为一种材料特性随空间位置连续梯度变化的新型多相材料，可使水下航行器壳体两侧呈现截然不同的性能与功能，使结构能够更好地适应超高温、大温度梯度等特殊极限环境。虽然国内外针对采用压电传感器、驱动器的智能结构主动控制进行了广泛研究，但是将压电材料用于FGM结构的主动控制研究相对较少，针对水下功能梯度材料板壳的主动控制文献则更少。代峰等[1]建立了一种用于温度梯度作用下功能梯度材料板壳力学性能分析的固体壳单元，针对压电传感器、驱动器的功能梯度材料板壳的热变形及振动的主动控制进行了数值仿真，探讨了组份材料体积分数幂指数分布、控制增益对功能梯度材料力学性能和控制效果的影响。Liew等[2-4]首先推导了含有压电传感器与作动器的FGM板的振动控制方程，针对温度变化和随厚度变化的功能梯度材料，采用位移—速度反馈算法从动态与静态两方面进行压电功能梯度材料的主动控制，并进行了试验验证。为了深入研究FGM材料应用于水下结构的主动控制，其力学行为是目前重要研究方向。

功能梯度梁、板和壳结构均有相应的解析解、半解析解和数值解的研究[5]。例如，于天崇等[6]研究了功能梯度材料面内变刚度矩形板的弯曲问题，该研究假定弯曲刚度沿板宽方向呈幂指数变化，设挠度为Levy解的形式求解基本方程。Zhang等[7]研究了含圆孔的功能梯度材料板的热应力问题，以圆孔中心为原点，假设杨氏模量、泊松比以及热膨胀系数关于原点的距离呈级数展开形式，以弹性力学中极坐标下的平衡方程、物理方程和本构关系为基本方程，求解出应力值。Yang和Gao[8]利用复变函数法和分层均匀化的思想，将平板在面内分为若干个均匀层，相邻层间位移与应力连续，求得了无限大含圆孔功能梯度板的应力解。杨正光[9]由压电动力学平衡方程导出以位移、电势及其一阶导数为状态变量的状态方程，由边界条件求得功能梯度压电圆板轴对称自由振动问题的精确解。Horgan与Chan[10]由平衡方程出发，假设弹性模量沿径向幂律变化，研究了功能梯度旋转圆盘及内外壁受压圆筒的轴对称变形问题。

可是，对于面内变刚度和小挠度功能梯度板弯曲问题的研究工作较少，这个问题的有限元解法也很少见。一般功能梯度材料的有限元解法多是将材料属性也构造为单元内的插值函数形式[11-12]的梯度有限元法，或将其分层均匀化计算[13]，或者直接用商业有限元软件进行计算[14-15]。分层方法与有限元软件方法类似，都是划分为很多个均匀单元，但是各单元内的材料参数不同，有一定的渐变关系，只有单元数量大才能不断接近准确结果。

本文尝试从经典薄板小挠度理论直接求解面内变刚度的功能梯度圆板的薄板弯曲问题，即利用经典薄板小挠度理论，首先推导出极坐标下的控制方程，然后针对无孔圆板和含圆孔圆板两种情况分别求解。而在有限元求解上，不使用梯度有限元法，而将材料参数的变化函数代替原来的常数，直接代入刚度矩阵计算，并提出了轴对称圆板问题的简易解法。通过将理论求解与有限元方法进行对比，发现两者吻合得非常好，表明本文的理论解具有一定的理论意义与应用价值。

1 基于薄板小挠度理论的FGM圆板理论求解

1.1 基本方程

如图1所示，以圆形薄板的中面为xy平面，圆板中心为原点，建立直角坐标系。

假设板厚一定，半径为a，上表面受均布力，不计体力，其杨氏模量沿圆板的半径方向变化，泊松比的数值量级小，与其他参数相比波动较小，因此其变化可以忽略不计，视为常数，则薄板的弯曲刚度可以写为如下形式：

由于考虑圆板问题，采用极坐标系更便于计算。极坐标系下坐标与直角坐标系下坐标（x，y）的关系为：

在本文研究的问题中，材料的杨氏模量仅沿半径方向变化，泊松比视为常数 μ，则应变 ερ、εφ、τρφ由应力 σρ、σφ、τρφ表示为

由经典板壳理论中的薄板小挠度弯曲理论假设[16]，可得ρ和φ方向的位移uρ、uφ：

其中：z为沿厚度方向的坐标，w（ ρ， ）φ 为z方向的位移，即挠度。

本文考虑轴对称圆板受轴对称载荷的情况，显然挠度函数也应为轴对称，仅与半径有关，与角度无关：

因此，uφ=0。由几何方程可得应变与位移的关系为

由本构方程（3）和（6）式得到应力的表达式：

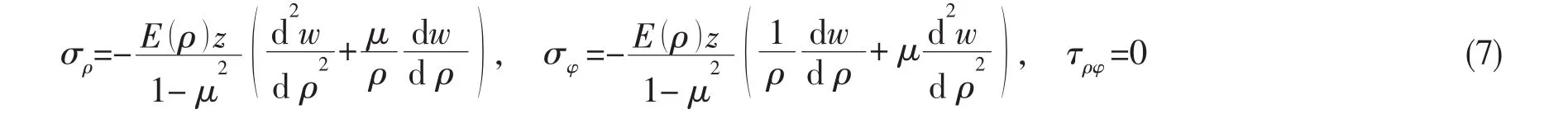
在薄板的每单位厚度上，将应力分量σρ、σφ沿厚度方向积分合成为弯矩Mρ、Mφ，应力分量τρφ合成为扭矩Mρφ，注意到积分过程中E（）ρ是面内的函数，与z方向的积分无关，于是得到：

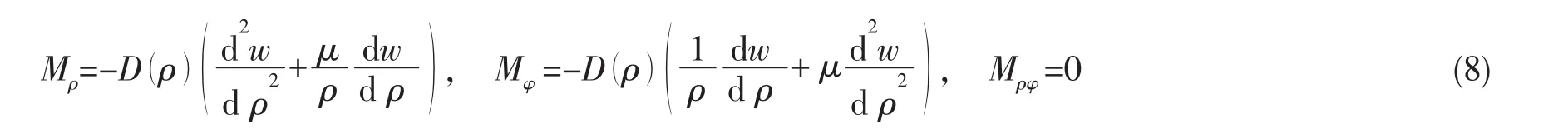
接下来由内力推导平衡方程，取出薄板的一个微分块的中面，如图2所示，以微分块中心的切向线为矩轴，可列出力矩平衡方程：

其中：Fsρ为横向剪力，将内力公式（8）代入（9）式得到：

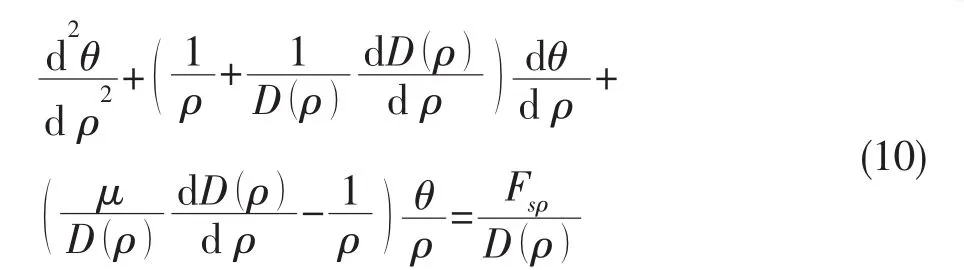
1.2 无孔圆板求解

假设无孔圆形薄板上表面受均布压力q0，取出半径为ρ的中间部分的薄板，由平衡条件可得：

将D（ρ）代入薄板控制方程（10）中得到：

将（13）式进行无量纲化，令 r=ρ/a得

注意到上述方程（14）是一个二阶变系数常微分方程，系数项与r的级数项有关，因此考虑用级数展开法求解，右端项采用泰勒级数展开：

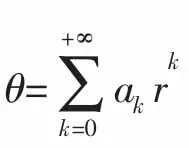
经过整理，（14）式按级数形式可以写成

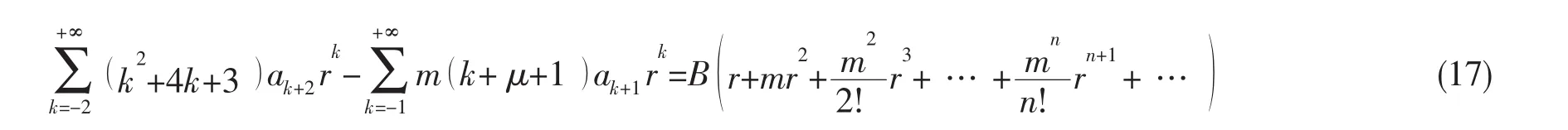
对于0≤r≤1均成立，所以r的各次项前的系数应相等，即可求出各项系数的关系。接下来从数学上证明此级数具有收敛性。

根据方程（17）可以求得如下结果：

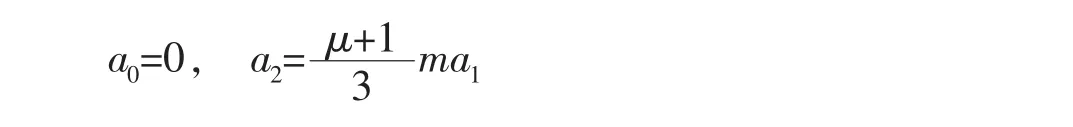
综上，该项级数是绝对收敛的。

而关于各个系数的求解，需要考虑边界条件，圆板周边设为固支边，应该满足边界位移和转角为零：

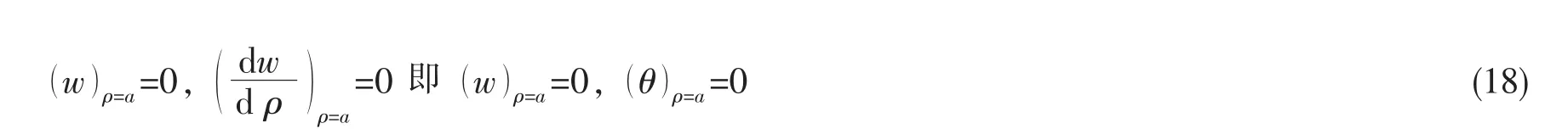
选取各项参数如下：

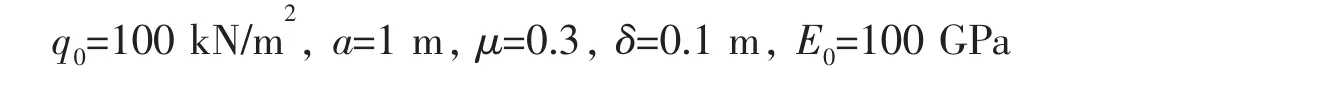
将上述参数代入方程，求解级数项中的系数。

当m=0，杨氏模量为常数，E=E0，即退化到了普通的圆形薄板，在经典弹性力学中有精确解：

代入数值求解得到

利用本文的方法求解出的结果与之完全一致。

1.3 中心含圆孔圆板求解

假设在该圆板的中心位置有一个与圆板同心的圆孔，内径为b，圆板半径仍为a，厚度为δ，上表面受横向均布载荷q0，圆板仍会发生轴对称弯曲。控制方程与之前的一致：

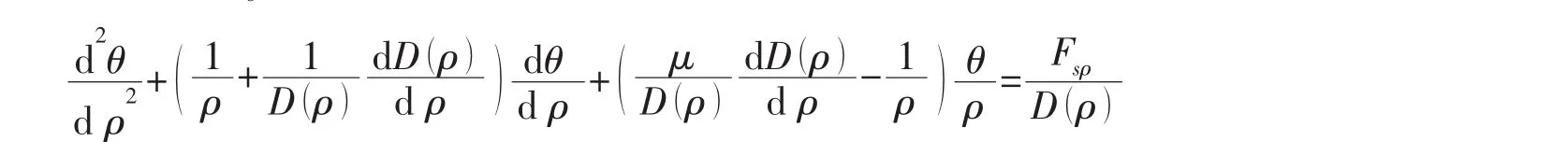
考虑与无孔圆板相同的边界条件，外边界固支，内边界自由。内外两个边界，四个边界条件为：

取出半径为ρ的中心部分，内边界自由，无剪力作用，根据z方向的力平衡方程有

（23）式右边项展开为如下形式：

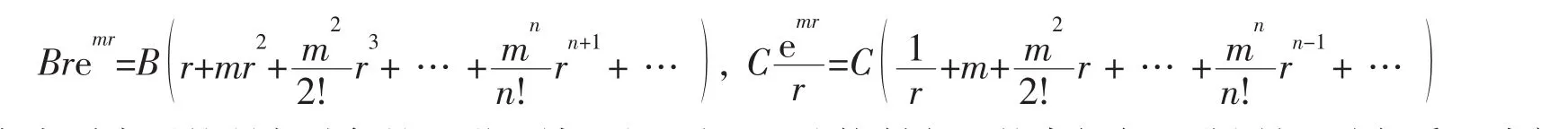
考虑到当下的研究对象是环形区域，因此对于上述控制方程的求解与无孔圆板不同，采用洛朗级数求解，不仅包括正次项系数，也包括负次项系数。将转角函数设为如下形式：

将（24）式代入方程（23）得：

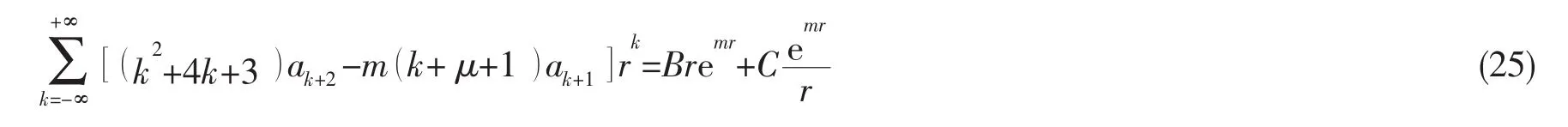
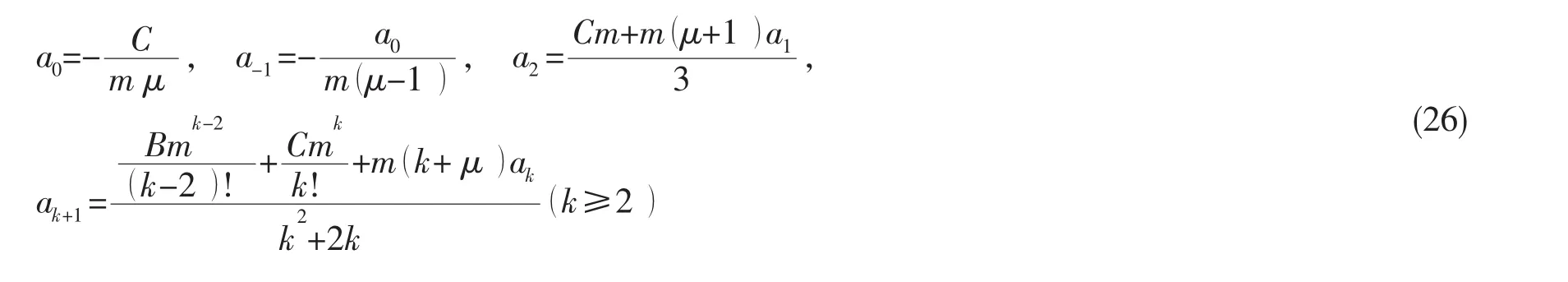
略去零系数项，转角函数（24）可以重新写为

则挠度函数为

注意到其中需要求解的未知系数仅为a1，c0两项，而条件中含有四个边界条件（20）-（21）式，分别为：

显然方程数大于未知数个数，需要对解进行优化，本文采用最小二乘法进行优化。若仅将a1，c0代入上述边界条件求解，显然很难完全满足边界条件，大大降低了求解精度，因此结合（26）式对所有系数进行优化。假设未知系数为a-1～an，c0。首先由（29b-29d）式求得：

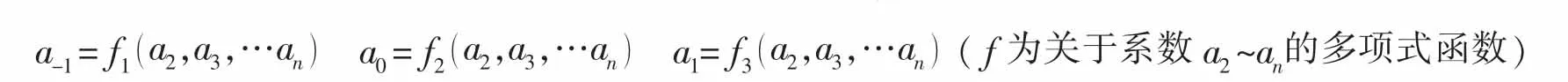
代入（26）式即可得到关于系数a2～an的n+1个方程，通过数学软件Maple的帮助使用最小二乘法求得系数 a2～an，然后由（29a-29d）求得 a-1、a0、a1和 c0。 代入数值求解：

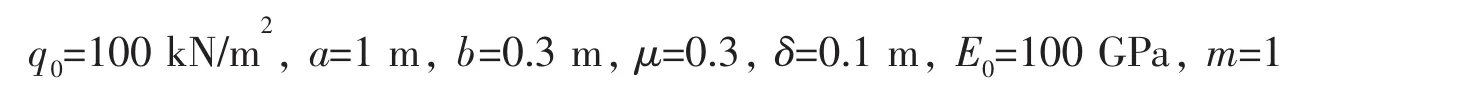
用上一节的方法同样可以验证级数收敛，由图3（b）可见，取级数展开的前十项系数即可。

2 有限元求解

本文研究的是面内变刚度的FGM轴对称圆形薄板受轴对称载荷的情况，因此本节用轴对称单元进行有限元编程计算。在实际求解过程中，只需要沿着半径方向划分单元，求得半径上各节点的挠度和转角值即可代表整个圆板的变形。在经典薄板小挠度弯曲理论中，忽略剪切变形，所以采用的单元为平面三节点环形单元。为与第一节结果对比，材料参数的变化函数一致，如第一节（11）式所示。

采用圆柱坐标系，半径方向为ρ坐标，轴向为z坐标，由于轴对称无需考虑角度坐标φ。

设w为z方向的位移 （挠度），a为圆板半径，圆板受均布载荷q0。将各参数无量纲化，令：

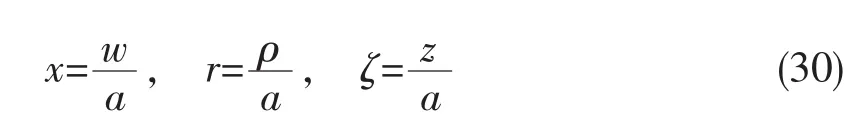
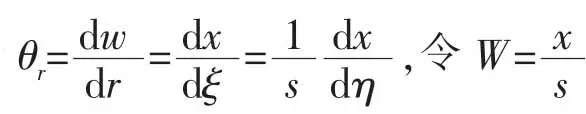
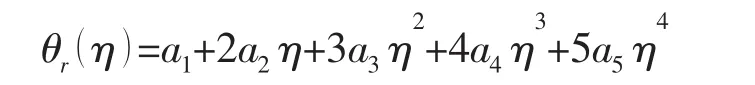
现在来考察位移模式的收敛性：

（1）完备性：薄板的位移由中面位移决定，位移W中含有的常数项代表了中面沿z轴的刚体位移，一次项代表了绕半径方向的刚体转动，由于轴对称，不考虑与角度相关的转动项。

（2）协调性：板壳问题的泛函包含挠度的二阶导数，因此插值函数应具有C1连续性，即位移W及其一阶导数在单元交界处连续。这里的环形单元，两个单元交界为前一单元的终点和后一单元的起点，径向坐标一致，显然求得的位移W和一阶导数均为常数，完全满足位移连续条件。综上可知，该位移模式能够满足有限元收敛条件。

将单元的三节点分别代入计算：

由于小挠度弯曲理论中所有变量都是挠度的函数，所以只需要得到W的形式即可求出所有变量。由上三式将W重新表示为：

按照基尔霍夫薄板小挠度弯曲假设，在轴对称圆柱坐标系下，εz、ερz、εzφ、ερφ均为零，应变为

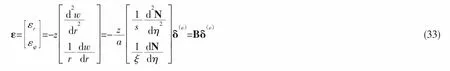
由本构方程可得应力为：

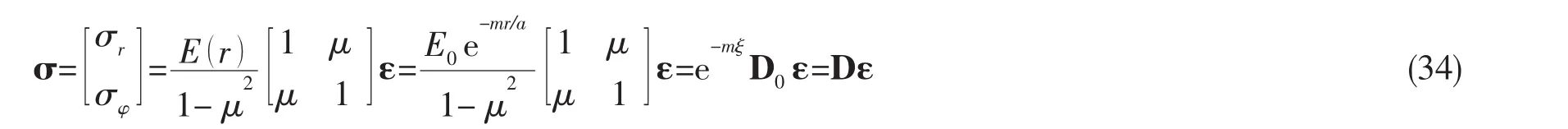
单元刚度矩阵为：

单元载荷矩阵为：

将单元刚度矩阵和单元载荷矩阵组装为总刚度矩阵和总载荷矩阵后，还需要设置边界条件。实心圆板外边界固支，因此设置最后一个单元的终点挠度、转角为零，并考虑到对称性，设置圆心处的转角为零。按照这个条件，采用置大数法，将总刚度矩阵中对应的对角线项设为大数，如1e30，从而在求解时使对应的自由度值为零。空心圆板外边界固支，内边界自由，只需设置最后一个单元的终点挠度、转角为零，对应总刚度矩阵对角项置大数，内边界无需外加条件。

对于以上各式的积分，采用六点高斯积分求解以保证准确性，然后采用高斯消去法求解线性方程组。解得各节点的位移值W、θr后，为与第一节结果对比，取挠度w=as·W，θ=-θr。

为了验证本文所提出的有限元法的准确性，在（34）式中设m=0，则FGM板退化为均质圆板，该种情况已有经典解，求解后对比挠度曲线如图5所示，实线为经典解，“■”代表有限元解，显然结果完全吻合，证明了本文有限元方法的可信性。

3 讨 论

3.1 有限元结果与理论计算结果比较

当m=1时，为FGM材料圆板，图6和图7分别为实心圆板和含圆孔圆板的结果对比。实线为第一节理论求解的结果，实心方块代表第二节有限元的计算结果。

由图6可见，利用两种方法求解的实心圆板的挠度曲线和转角曲线完全吻合。图7中，圆板中心含圆孔时，从内边界至外边界划分单元，内边界自由，不加另外的边界条件，孔洞半径和圆板尺寸均与第一节相同。两种方法求得的曲线趋势一致，在内边界处的误差最大，随着半径的增大，误差逐渐减小。在内边界r=0.3 m处，有限元的计算结果为挠度值3.03E-4m，转角值为5.55E-4，而利用前文的理论求解得挠度值为3.113E-4m，转角值为5.92E-4，挠度误差约为2.73%，转角误差约为6.6%。李尧臣的论文[15]中计算了面内变刚度矩形板，并利用商业有限元软件计算，误差约为10%，本文的有限元方法更加准确，理论解与之的误差可能源于1.3节中因超定方程采用了解的优化，无法完全保证所有方程精确满足。

3.2 含孔圆板与不含孔圆板比较

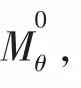
3.3 杨氏模量变化对薄板变形的影响

显然孔周的弯矩变化与圆板杨氏模量的变化函数有关。上例中设定E=E0e-ρ/a，从圆心开始沿半径向外杨氏模量递减。改变杨氏模量的变化规律，可以有效减小薄板的变形和孔边的弯矩。

图9和图10分别为在m取不同的值，从1变到-1时挠度和弯矩变化。由图线可以明显看到当m从1开始不断减小，挠度逐渐减小，薄板的弯曲变形程度变小，孔边的弯矩逐渐减小，整板的弯矩都有明显的减小。m=0时为均质板的特殊情况，而m变为负数，杨氏模量沿半径方向增大，挠度和弯矩比均质板的情况更进一步减小。由此可见，适当改变功能梯度材料的结构变化规律，可有效改善孔边及整个结构的受力情况。

4 结 论

本文讨论了杨氏模量随半径呈指数函数形式变化时，圆形薄板和中心含圆孔的圆形薄板受均布载荷发生轴对称弯曲的级数解和有限元解。与前人的方法对比，本文所用的方法更具有普适性，对于任意杨氏模量的变化均可求解，且不只局限于面内变参数的功能梯度材料，对于连续变厚度的平板亦能适用，求解过程更直接可行，计算结果的精确度也有一定保证。