一种能准确模拟波浪复杂演化过程的非静力学数值模型
2018-11-30陈善群汤润超
陈善群,吴 昊,汤润超
(安徽工程大学 建筑工程学院,安徽 芜湖241000)
0 引 言
众所周知,波浪由深水区向沿岸浅水区传播过程中会出现波浪折射、波浪衍射、波浪浅化及波浪破碎等复杂现象。如何准确模拟这些复杂现象一直是港口、海岸及近海工程等相关研究领域的热点问题。
目前比较成熟的波浪模拟数值模型有两大类别。一类是基于Boussinesq方程的波浪数值模型,该类模型具有非线性和色散特性,能准确有效地模拟波浪的演化过程,尤其在浅水区的波浪演化过程的模拟上已体现出较大优势[1-2]。目前该类模型的研究拓展主要集中于色散精度的提高[3-4]、湍流模型的加入[5]、自由面溶质的影响及输运[6]等几个方面。这些研究拓展的实现需在原数值模型内加入大量的附加控制方程,使得控制方程组的求解难度明显增加,一定程度上阻碍了该类波浪数值模型的持续性发展。另一类是直接求解Navier-Stokes方程组结合自由面追踪技术来模拟波浪的演化过程。该类模型具有适用性强,精度较高等优点,已在工程实际中得到大量使用[7-9]。但研究者们发现该类模型同样存在明显缺陷,主要体现在:(1)消耗大量计算机时,难以拓展到大尺度计算域;(2)自由面压力边界的准确求解难度较大,直接影响自由面速度场的准确性;(3)计算网格一般采用笛卡尔坐标系,难以准确贴合自由面和不规则区域,直接影响求解准确性等几个方面。
综合上述两类波浪数值模型的优点与不足,研究者们另行发展了一类非静力学波浪数值模型[10-15]。该类模型的主要特点有:(1)建立自由面竖直方向水位与横向坐标的函数关系,减少自由面追踪消耗的大量计算机时;(2)控制方程采用非静力学方程,方程中的压力被分解成静力学压力和非静力学压力两部分,可结合有限体积或有限差分方法对控制方程进行离散求解。研究表明,该类模型非常适用于自由面压力边界的准确求解,并在浅水区波浪演化过程、自由面湍流运动以及溶质输运等方面的数值计算中都取得了较好的效果。
另外,针对早期非静力学数值模型中存在的竖直方向网格数较少使得波浪的色散特性难以被准确评估的难点问题,研究者们普遍认为竖直方向顶层计算单元压力的准确求解是解决问题的关键。为此,Stelling和Zijlema[16]提出了一种Keller-box网格划分方法替代常用的交错网格,使得压力处于计算单元界面位置而不再处于计算单元中心位置。这样做无需近似,自由面的压力可精确设置为零。Yuan和Wu[17]提出了一种交错网格框架下的积分方法,直接避免了竖直方向顶层计算单元的静力学压力设定问题。Young和Wu[18]对类Boussinesq型方程进行解析近似求解,结合参考速度,得到了竖直方向顶层计算单元非静力学压力分布。以上研究成果已在一定程度上妥善解决了竖直方向网格数较少使得波浪的色散特性难以被准确评估的难点问题。然而,早期非静力学数值模型在模拟碎波带波浪演化及破碎波浪沿斜坡爬高等波浪复杂演化过程时遇到的难以准确模拟的问题仍没有得到妥善解决。Zijlema和Stelling[19]则认为需在非静力学模型中结合适当的激波捕捉算法来实现对波浪复杂演化过程的准确模拟。与此同时,Godunov型格式[20-23]作为一类成熟的激波捕捉算法已在含有间断流动的计算流体力学问题中得到广泛使用。大量算例证明,Godunov型格式无需添加任何判据,就具有直接判定并准确捕捉波浪破碎位置的能力,被认为是准确模拟波浪复杂演化过程的理想数值算法。
本文拟在早期非静力学波浪模拟数值模型的基础之上,结合研究者们对数值模型的改进方法,并在数值模型中附加Godunov型格式以实现激波捕捉,发展一种能准确模拟波浪复杂演化过程的非静力学数值模型。该数值模型控制方程采用笛卡尔坐标系下的不可压缩Navier-Stokes方程组。为准确模拟计算域不规则底部与自由面之间水体的运动,使用σ坐标系对笛卡尔坐标系进行坐标变换,后续采用有限体积和有限差分混合方法结合Godunov型格式对控制方程进行离散求解。为便于结合Godunov型格式,数值模型中速度变量定义在计算单元的中心位置,同时将非静力学压力定义在计算单元竖直方向界面位置。为进一步提高数值模型的时空分辨率,计算单元界面的通量计算采用HLL黎曼求解器,时间步迭代采用二阶非线性强稳定性保持龙格库塔(SSP Runge-Kutta)格式。后续拟将非静力学数值模型用于经典波浪复杂演化问题的数值模拟,并与解析解或实验结果进行对比,验证该数值模型的准确性与适用性。
1 控制方程
本文选取三维笛卡尔坐标系下的不可压缩Navier-Stokes方程组作为非静力学数值模型的控制方程,表达式如下:

为准确贴合计算域不规则底部及自由面,本文采用Lin和Li[24]提出的σ坐标系对笛卡尔坐标系进行坐标变换,变换的表达式为:


将变换式(3)代入笛卡尔坐标系下的控制方程((1)式)后推导得到σ坐标系(x,y,σ)下的控制方程,表达式为:

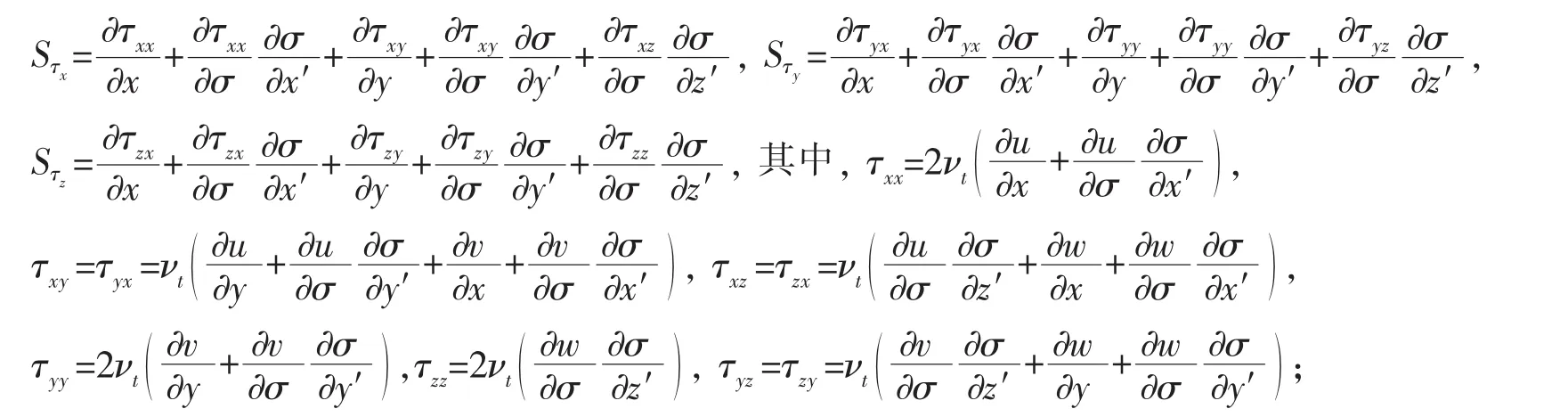
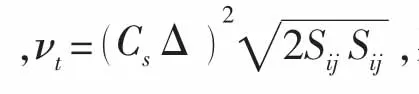
连续性方程((5)式)通过积分结合竖直方向速度ω需满足的边界条件,可得σ坐标系下自由面运动控制方程,表达式如下:

2 控制方程的离散求解
本文采用有限体积和有限差分混合方法结合Godunov型格式对控制方程((6)式)进行离散求解。为便于结合Godunov型格式,选用一种另类的交错网格框架来划分计算域,其中速度变量定义在计算单元的中心位置,非静力学压力定义在计算单元竖直方向界面位置,具体如图2所示。以下章节为具体阐述控制方程的离散求解过程。
2.1 时间步迭代
为获得二阶时间精度,本文的时间步迭代选取Gottlieb等[25]提出的两段式SSP Runge-Kutta格式,具体过程如下:
第一阶段,采用一种常见的一阶精度两步投影法对(6)式进行时间离散,获取中间量U()1:
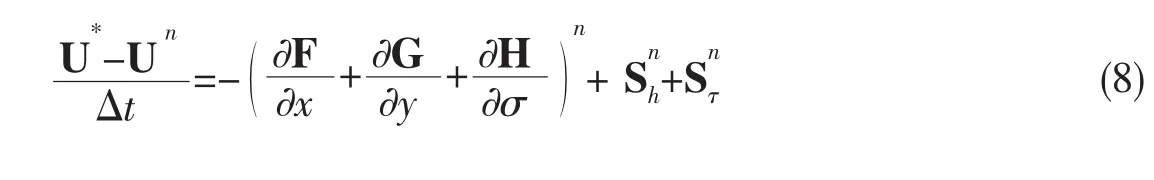

式中:Un代表时间步n时U的取值;U*为两步投影法计算格式中的中间量;U()1为经过第一阶段迭代计算后得到的中间量。
第二阶段,利用上阶段采用的投影法对(8)式再次进行迭代计算(两段式的两步投影法构成二阶非线性强稳定性保持龙格库塔(SSP Runge-Kutta)格式),获取时间步n+1时U的取值Un+1:
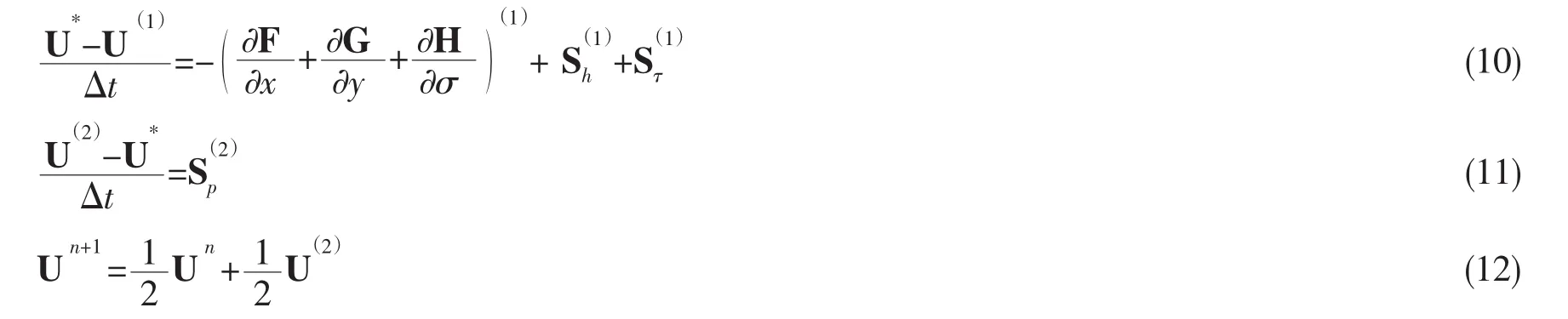
(9)式与(11)式中的Sp为非静力学压力源项,非静力学压力p需通过求解Poisson方程得到,Poisson方程的推导与求解将在后续章节中阐述。
(8)式与(10)式中的 Δt为自适应时间步长,满足 Courant-Friedrichs-Lewy (CFL)条件,Δt的表达式为:
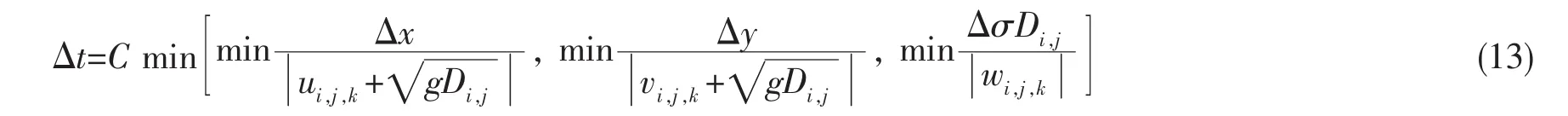
式中:C为Courant常数,为保证数值模型计算的精度和稳定性,C取值0.5。
2.2 空间离散
本文选取Liang和Marche[26]提出的二阶Godunov型有限体积方法对(8)式与(10)式进行空间离散求解,具体过程如下:
首先对通量F和G以及源项Sh进行修正,将D=h+η代入源项Sh的表达式,对Sh进行简单分解:

将通量F和G分别与(14)式和(15)式等式右边的第一项相减后,可得修正后的通量F和G以及源项Sh的表达式:
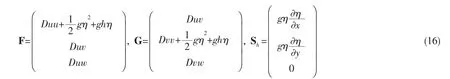
接下来对计算单元i中的守恒变量U进行分段线性空间重构,以x方向为例:

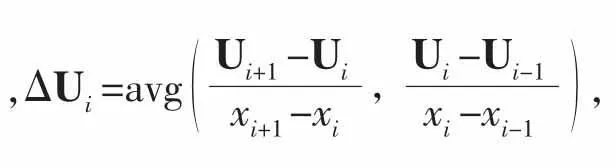
守恒变量U在计算单元界面i+1/2左侧和右侧的估值分别为:
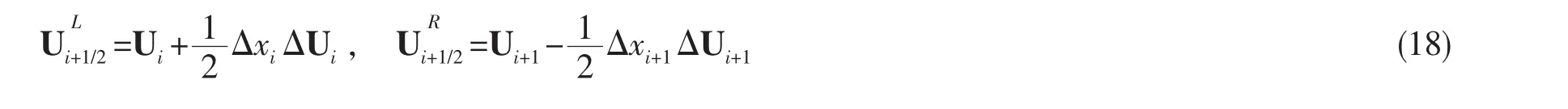
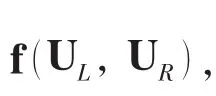

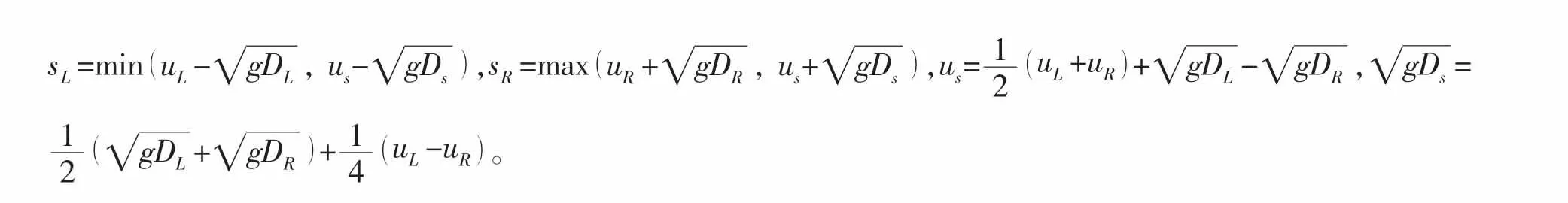
从(9)式与(11)式中可以看出,非静力学压力p是求解非静力学速度场(u,v, )w 的前提,两者之间存在明显的依赖关系,表达式为:

式中:m=1,2代表两段式SSP Runge-Kutta格式中的阶段数。
求解非静力学压力p所需的Poisson方程由连续性方程((5)式)演化得来,先将(3)式和(4)式代入(5)式,得出连续性方程((5)式)的坐标变换形式:

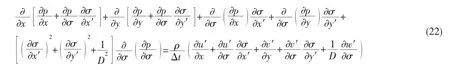
采用二阶中心有限差分方法对(22)式进行空间离散,得到对应的线性方程:
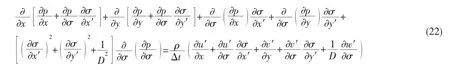
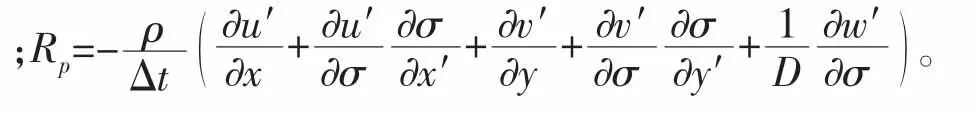
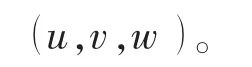
2.3 边界条件
(1)自由面边界条件
不考虑附加风效应,自由面切向应力应等于零,同时自由面竖直方向速度w满足运动学边界条件,以及自由面的非静力学压力p在求解Poisson方程时应设置为零,即:


(2)计算域底部边界条件
计算域底部法向速度w满足运动学边界条件,同时水平方向速度满足滑移边界条件,以及计算域底部剪切应力满足粗糙固壁边界条件,即:

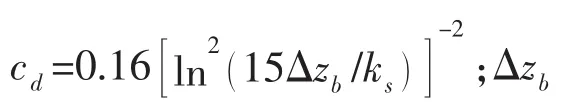
计算域底部非静力学压力p满足Neumann边界条件,即:

(3)其余边界条件
竖直方向边界是固壁时,满足滑移边界条件,即法向速度和切向应力设置为零,法向压力梯度设置为零;竖直方向边界为波浪入口边界时,自由面高程和速度大小通过解析解来施加;侧向边界满足滑移边界条件。
3 算例验证
3.1 淹没式堤坝上波浪传播
为验证非静力学数值模型对波浪浅化等复杂演化过程模拟的精确性与适用性,选取Beji和Battjes[28]关于淹没式堤坝上周期性波浪传播过程的水槽实验作为研究对象。根据Beji和Battjes的实验装置,建立相应的计算域,如图3所示。其中,计算域分为波浪水槽和消波区两部分。波浪水槽长25.0 m,高0.6 m,水槽中静水高度初始为0.4 m,淹没式堤坝外形为梯形,高度为0.3 m,堤坝向波坡面坡度1:20,背波坡面坡度1:10。波浪水槽中初始水位距堤坝顶部0.1 m。消波区位于波浪水槽右部,长10.0 m,采用Larsen和Dancy[29]提出的海绵层消波技术。数值水槽左边壁为周期性波浪入口边界,选取周期T=2.02 s,振幅A=1.0 cm和周期T=1.25 s,振幅A=1.2 cm两种规则波形条件。数值水槽内共设置a-f六个水位监测点,距离水槽左边壁的距离xa-xf分别为10.5 m、12.5 m、13.5 m、14.5 m、15.7 m和17.3 m。计算域水平方向网格数为1750,竖直方向网格数为3,计算单元总数为5250。
图4和图5分别给出了周期T=2.02 s,振幅A=1.0 cm和周期T=1.25 s,振幅A=1.2 cm两种波形条件下a-f六个水位监测点自由面高程数值计算与实验结果的对比。从图中可以看出,两种波形条件下,非静力学数值模型对六个监测点的自由面高程预测结果与Beji和Battjes的实验结果整体吻合较好。另外,从图4(c)-(f)中可以看出,对于淹没式堤坝上波浪传播过程中出现非线性浅水波这一复杂演化现象,非静力学数值模型同样能较准确地模拟。
3.2 孤立波沿斜坡爬高
3.3 海底滑坡诱发海啸
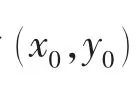

滑坡体轮廓曲线为截断双曲正割函数,满足关系式:

式中:ut=1.17 m/s,为滑坡体的自由沉降速度;a0=1.12 m/s2,为滑坡体初始加速度。
图9给出了海底滑坡诱发海啸过程中四个水位监测点 (x0,y0)自由面高程数值计算与实验结果的对比。图中tC=0.900+7.07d,为文献[31]给出的经验参考时间。从图中可以看出,非静力学数值模型对四个监测点的自由面高程预测结果与Enet和Grilli的实验结果整体吻合较好。对于海底滑坡诱发海啸过程,非静力学数值模型能较准确地数值模拟。
据由Enet和Grilli的实验数据可拟合得出滑坡体的运动方程,关系式为:
4 结 论
针对早期非静力学波浪模拟数值模型的不足之处,结合研究者们对数值模型的改进方法,并在数值模型中附加激波捕捉Godunov型格式,本文发展了一种能准确模拟波浪复杂演化过程的非静力学数值模型。该数值模型选取σ坐标系下的不可压缩Navier-Stokes方程组作为控制方程,利用σ坐标系贴合不规则底部与自由面之间的计算域;为便于结合Godunov型格式,将速度变量定义在计算单元的中心位置,同时将非静力学压力定义在计算单元竖直方向界面位置;采用有限体积和有限差分混合方法结合Godunov型格式对控制方程进行空间离散;为进一步提高时空分辨率,利用HLL黎曼求解器求解计算单元之间的通量以实现激波捕捉,并采用二阶非线性强稳定性保持龙格库塔(SSP Runge-Kutta格式)进行时间步迭代。将非静力学数值模型用于数值模拟淹没式堤坝上波浪传播、孤立波沿斜坡爬高和海底滑坡诱发海啸三个波浪复杂演化过程,数值计算结果与相应的实验结果较为吻合,说明该非静力学模型对波浪浅化、波浪破碎、滑坡诱发海啸等复杂现象的数值模拟具有较高的精确性和适用性,可望为波浪复杂演化过程的数值模拟提供一种较为准确有效的研究手段。
