基于幂次平均的离散归一化总梯度法

王彦国 吴姿颖 邓居智 杨亚新 黄 松 罗 潇

(东华理工大学放射性地质与勘探技术国防重点学科实验室，江西南昌 330013)

1 引言

位场数据处理是重磁资料进行地质—地球物理综合解释的基础，而反演是数据处理的重要环节。常用的位场反演方法包括基于网格剖分的物性反演法和快速自动反演方法。

基于网格剖分的物性反演方法是基于反演理论、在最小二乘意义下使目标函数达到极小的(非)线性反演。这类方法需要引入先验约束条件，需大量的计算机内存和较长的计算时间，制约着这类反演方法的应用，尤其在地质勘探程度较低的地区或无地质约束区域，难以获得良好的反演结果[1]。近年来，Li等[2]、姚长利等[3,4]提出的改进措施在一定程度上提高了这类方法的计算效率，改善了反演效果。

常用的快速自动反演方法主要有欧拉反褶积法和归一化总梯度法，该类方法可以在无地质约束条件下快速计算场源参数信息。其中，欧拉反褶积是以位场和位的导数满足欧拉齐次方程为理论基础，由Peters[5]首先提出，Thompson[6]进一步完善，Reid等[7]推广至三维资料处理中的一种反演方法。该方法能自动或半自动地反演出场源质心、上顶或边界位置，还可以利用反演的构造指数推断场源的几何形状。由于该方法具有较强的灵活性和实用性，目前已成为了地球物理工作者常用的反演方法和重磁资料解释工具。但事实上，欧拉反褶积是一个灵敏度较高的方程式，导数计算结果或计算点位稍有偏差，便会使反演结果产生较大的偏离，从而影响反演精度[8]。近年来，国内外学者对欧拉方程进行了各种形式的改进：与解析信号相结合的An-EUL反演法[9]，与Tilt angle相结合的Tilt-Euler法[10],以及其他的改进措施[11-16]，这些改进方法在一定程度上提高了欧拉反褶积法的可靠性。归一化总梯度法是建立在导数换算和向下延拓基础之上的归一化形式，是由前苏联学者别列兹金提出，该方法对油气储集层有着较好的识别效果[17]； 肖一鸣等[18，19]将该方法引进到国内，并介绍了初步应用情况； 侯重初等[20]用傅氏变换代替傅氏级数计算归一化总梯度，并进行了详细的模型试算；张凤旭等[21]利用Hilbert变换计算了重力归一化总梯度，在理论上提高了异常分辨率；肖鹏飞等[22]利用积分迭代法进行归一化总梯度中向下延拓的稳定计算；张凤琴等[23]采用了DCT变换计算重力归一化总梯度；郭灿灿等[24]利用泰勒级数迭代法代替积分迭代法，进行归一化总梯度的向下延拓计算；苏超等[25]采用几何平均代替算术平均进行空间总梯度的归一化处理。这些改进措施在一定程度上提高了归一化总梯度法的计算稳定性和反演精度，然而，该方法仅能识别浅部地质体的位置信息，无法反映出深部地质体的深度信息，或计算的深度值与真实值偏差过大，也无法判断场源的几何形状。

针对常规归一化总梯度法的缺点，本文提出了基于幂次平均的离散归一化总梯度法，并通过模型试验和实际资料处理验证了方法的可行性、有效性和实用性。

2 基本原理

2.1 传统归一化总梯度法

传统归一化总梯度法是别列兹金提出的，其表达式为

(1)

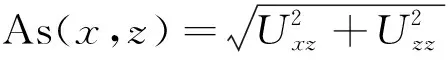
(2)

(3)

2.2 迭代滤波

由于导数换算和向下延拓都会不同程度地放大高频干扰成分，需要通过低通滤波增强计算结果的稳定性。传统的低通滤波算子是别列兹金提出的圆滑滤波因子

(4)

式中：N为谐波数；k=1,2,…,N。该滤波因子在压制高频成分时，低频成分在一定程度上也有所削弱。为此，本文选择如下迭代滤波因子提高延拓的计算精度和稳定性

(5)

式中：α为正则化因子，α越大，对高频成分压制越强，一般情况下α≥1(本文取α=1)；n为迭代次数。

将式(5)代入式(3)，有

(6)

2.3 幂次平均归一化总梯度

传统归一化函数MAs(z)为算术平均，本文采用幂次平均代替算术平均进行归一化处理，即

(7)

式中p为幂次数，当p=1时，EAs(z)便是算术平均MAs(z)。不同形状的地质体具有不同的最佳p值，p=1对应水平圆柱体，p=2对应岩脉，p=4则对应台阶(下文模型试验将予以证实)。基于幂次平均的归一化总梯度表达式为

(8)

2.4 归一化总梯度的离散化

由于式(1)和(8)只能识别最浅部的地质体信息，较深部的地质体则无法被同时检测出来，或计算结果与实际情况偏差过大。为了提高方法的实用性，下面对式(8)进行离散化处理。

设观测面上存在Q个明显的解析信号As的极大值，将测线离散成Q段，每段包含一个解析信号极大值，两个极大值之间的极小值点定义为离散点(图1)。

那么，离散化后第q段的归一化总梯度为

(9)

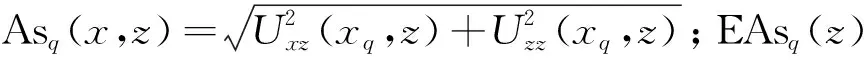
图1 离散化处理示意图

2.5 方法实现步骤

基于幂次平均的离散归一化总梯度计算流程如下：

(1)给定初值迭代次数n(可取1)，采用迭代滤波法计算地下空间的导数Uxz(x,z)、Uzz(x,z)及As(x,z)；

(2)根据As(x,0)的异常形态，利用极大值个数将测线离散成Q段；

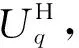
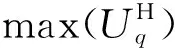
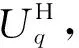
(6)改变区间段位置，重复上述步骤(3)～(5)，完成所有区间段的计算；

3 模型试验

3.1 幂次数与地质体几何形状关系

为了验证幂次数与地质体形状存在相关性，分别设计了台阶、岩脉和无限长水平圆柱体等三种常用二度体模型进行试验，并通过改变地质体参数进一步说明这种相关性。

3.1.1 水平圆柱体模型

建立两个单一水平圆柱体模型，模型1、模型2的质心埋深分别为1km、2km，磁化倾角分别为45°和90°，半径均为0.5km。图2给出了这两个水平圆柱体模型经磁异常转换得到的max(UH)及其对应的深度值与迭代次数n和幂次数p的关系曲线。从图2a、图2c可以看出，无论p取何值，max(UH)均随迭代次数n的增加而先增大后减小，存在一个极值点； 当幂次数p增大时， max(UH)逐渐减小。从图2b、图2d可以看出，max(UH)对应的深度值随迭代次数增加先缓慢递增，再迅速增大，存在一个明显的转折点，而该转折点对应的深度值与max(UH)曲线上极大值对应的深度值一致。由于p=1与p=2时max(UH)曲线上极大值对应的深度值相同，因此可认为圆柱体的最佳幂次数p为1，此时最佳迭代次数的max(UH)对应的深度值分别为0.9km和1.8km，均与模型深度1.0km和2.0km存在10%的相对误差。图3a、图3b分别是两个水平圆柱体模型磁异常归一化总梯度场，可以看出，UH场关于水平圆柱体质心埋深位置左右呈对称分布，极大值圈闭位置与圆柱体质心位置基本吻合。

3.1.2 岩脉模型

构建了两个岩脉模型(岩脉1、岩脉2)，岩脉的倾斜度分别为45°和90°，上顶埋深分别为1.0km、2.0km，磁化倾角分别为45°和90°。图4是两个岩脉模型经磁异常转换得到的max(UH)及其对应的深度值与迭代次数n和幂次数p的关系曲线。从图4a、图4c可以看出，max(UH)仍随迭代次数n的增加而先增大后减小，存在一个极值点；当幂次数p增大时， max(UH)同样逐渐减小。从图4b、图4d可以看出， max(UH)对应的深度值也随迭代次数增加而先缓慢递增，然后迅速增大，存在一个明显的转折点，而该转折点对应的深度值与max(UH)曲线上极大值对应的深度值基本一致。由于p=2与p=3时max(UH)曲线上极大值对应的深度值相同，因此岩脉的最佳幂次数p=2，此时最佳迭代次数下的max(UH)所对应的深度值分别为1.0km和1.9km，与模型深度1.0km和2.0km基本吻合。图5是两个岩脉模型的磁异常归一化总梯度场，可见UH场关于岩脉上顶埋深位置左右呈对称分布，极大值圈闭位置与模型上顶埋深位置基本重合。

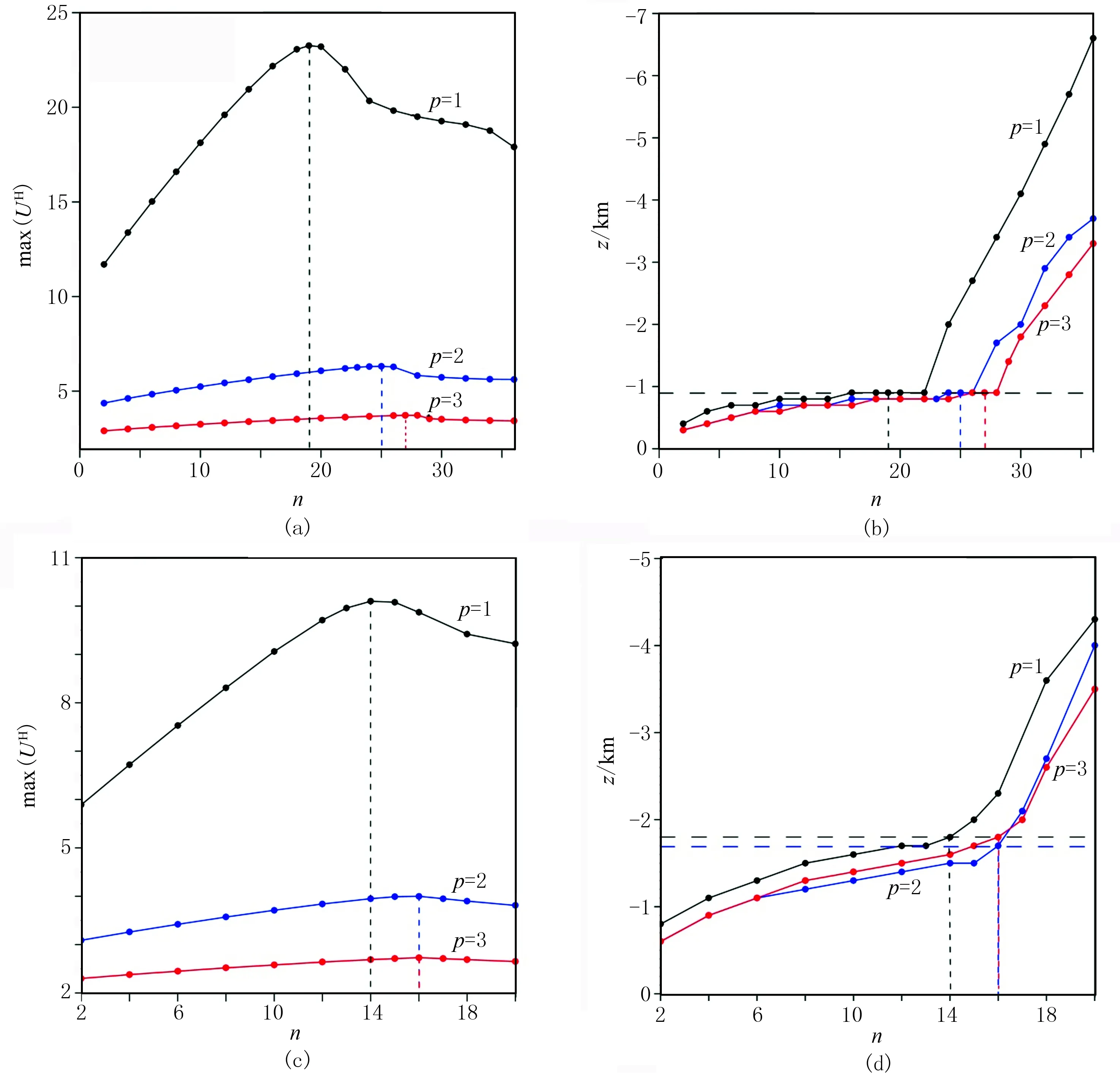
图2 两个水平圆柱体模型的max(UH)及其对应的深度随p和n的变化曲线(a)模型1 max(UH)随参数p和n的变化曲线； (b)模型1 max(UH)对应的深度值随参数p和n的变化曲线；(c)模型2 max(UH)随参数p和n的变化曲线； (d)模型2 max(UH)对应的深度值随参数p和n的变化曲线

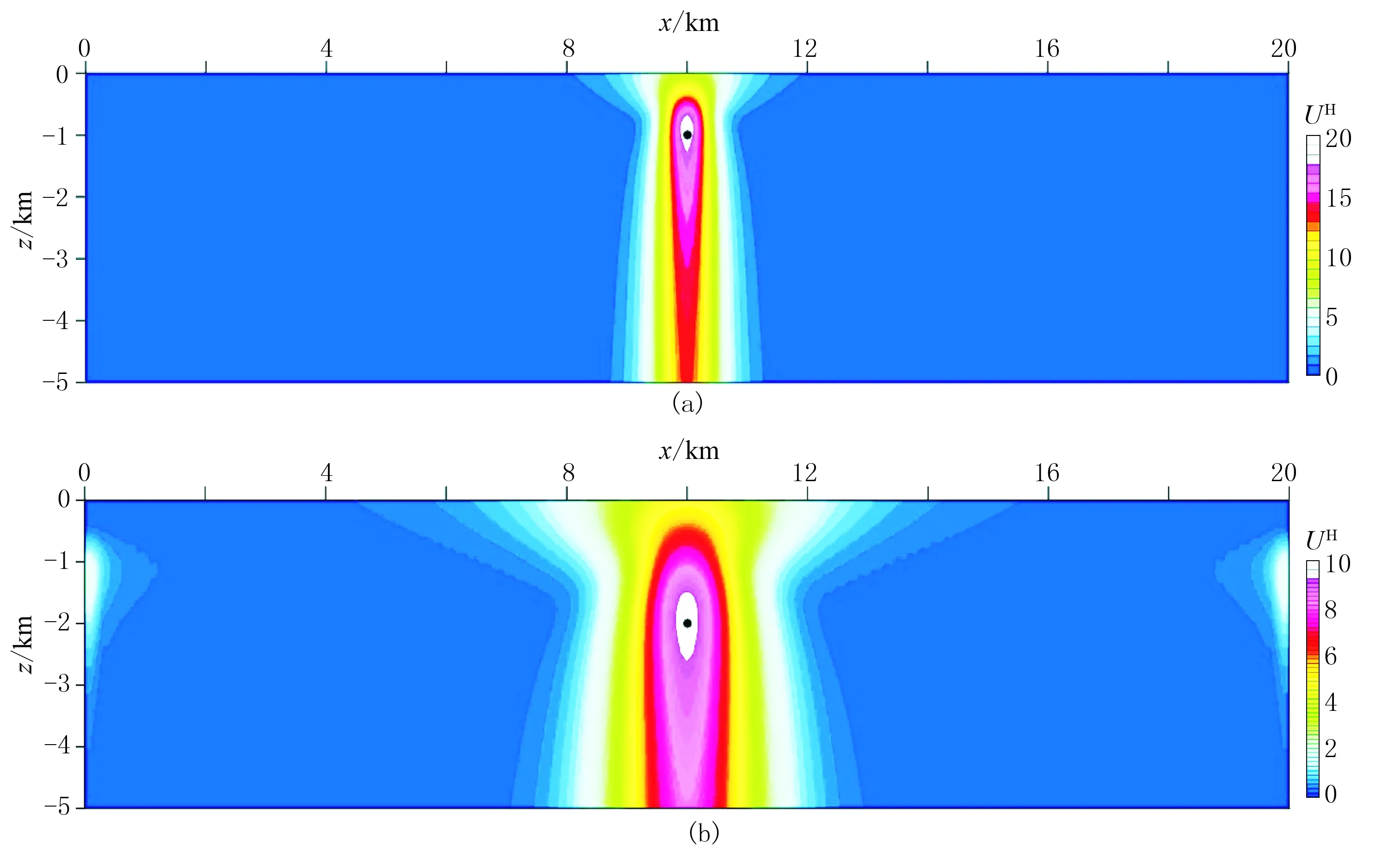
图3 水平圆柱体模型1(a)及模型2(b)磁异常幂次平均归一化总梯度场

图4 岩脉模型1 max(UH)随p和n的变化曲线(a)、 岩脉模型1 max(UH)所对应的深度随p和n的变化曲线(b)、 岩脉模型2 max(UH)随p和n的变化曲线(c)及岩脉模型2 max(UH)所对应的深度随p和n的变化曲线(d)

图5 岩脉模型1(a)、岩脉模型2(b)磁异常幂次平均归一化总梯度场

3.1.3 台阶模型

台阶模型1、模型2的倾斜度分别为45°和60°，上顶埋深分别为1.0km和2.0km，磁化倾角分别为30°和60°。图6为两个台阶模型的磁异常max(UH)及其对应的深度与迭代次数n和幂次数p的关系曲线。从图6a、图6c可以看出，max(UH)均随n的增加而先增大后减小，存在极值点； 当幂次数p增大时，max(UH)则逐渐减小。从图6b、图6d可以看出，除p=1外，在其他p值时，max(UH)所对应的深度随迭代次数的增加先逐渐增大，当达到最佳迭代次数后迅速增大，因此max(UH)所对应的深度曲线在最佳迭代次数时存在一个明显的拐点； 最佳迭代次数时max(UH)所对应的深度随p值的增加逐渐接近模型埋深，由于p=4与p=5时的最佳迭代次数下的max(UH)所对应的深度相同，因此认为p=4是台阶模型的最佳幂次数，此时max(UH)所对应的深度分别为1.1km和2.1km，均略大于模型深度1.0km和2.0km。图7是上述两个台阶模型磁异常归一化总梯度场等值线图，可以看出，UH关于台阶上顶埋深位置左右呈对称分布， max(UH)所对应的位置与台阶上顶埋深位置基本吻合。

上述三组模型试验结果表明，基于幂次平均的归一化总梯度法是可行的，可以有效地识别不同形状地质体的深度参数； 不同几何形状的地质体对应的最佳幂次数是不同的，可利用该特点估计地质体类型；归一化总梯度场的分辨率随着地质体埋深增加而有所降低。

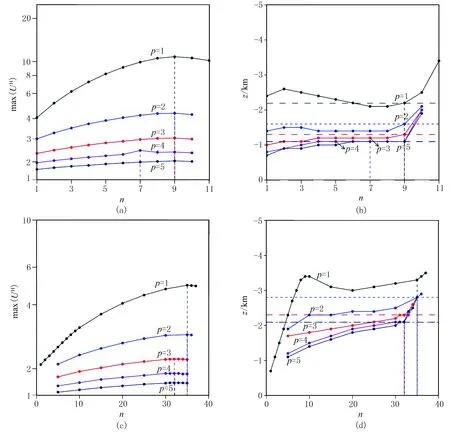
图6 台阶模型1 max(UH)随p和n的变化曲线(a)、 台阶模型1 max(UH)所对应的深度随p和n的变化曲线(b)、台阶模型2 max(UH)随p和n的变化曲线(c)及台阶模型2 max(UH)所对应的深度随p和n的变化曲线(d)

3.2 叠加模型试验

为了进一步验证新方法的有效性，设计了一个叠加组合模型，组合模型包含了三个不同类型的地质体。地质体1为台阶模型，上顶坐标为(10km，2km)，倾斜角度为60°，磁化倾角为30°，磁化强度为0.1A/m；地质体2为垂直岩脉模型，上顶坐标为(20km，0.5km)，磁化倾角为45°，磁化强度为1A/m；地质体3为水平圆柱体，质心坐标为(30km，1km)，磁化倾角为60°，磁化强度为1A/m。图8是该组合模型产生的磁异常及磁异常的解析信号，从解析信号可以看出地下存在三个明显的磁异常体。图9是整条剖面及离散化剖面的磁异常max(UH)及其对应深度与迭代次数n和幂次数p的关系曲线，从图9a和图9b中可以看出，幂次数p=2与p=3时最佳迭代次数下的max(UH)对应的深度一致，即最佳幂次数p为2时，此时max(UH)对应的坐标为(20.0km，0.5km)，与岩脉上顶埋深位置完全一致。

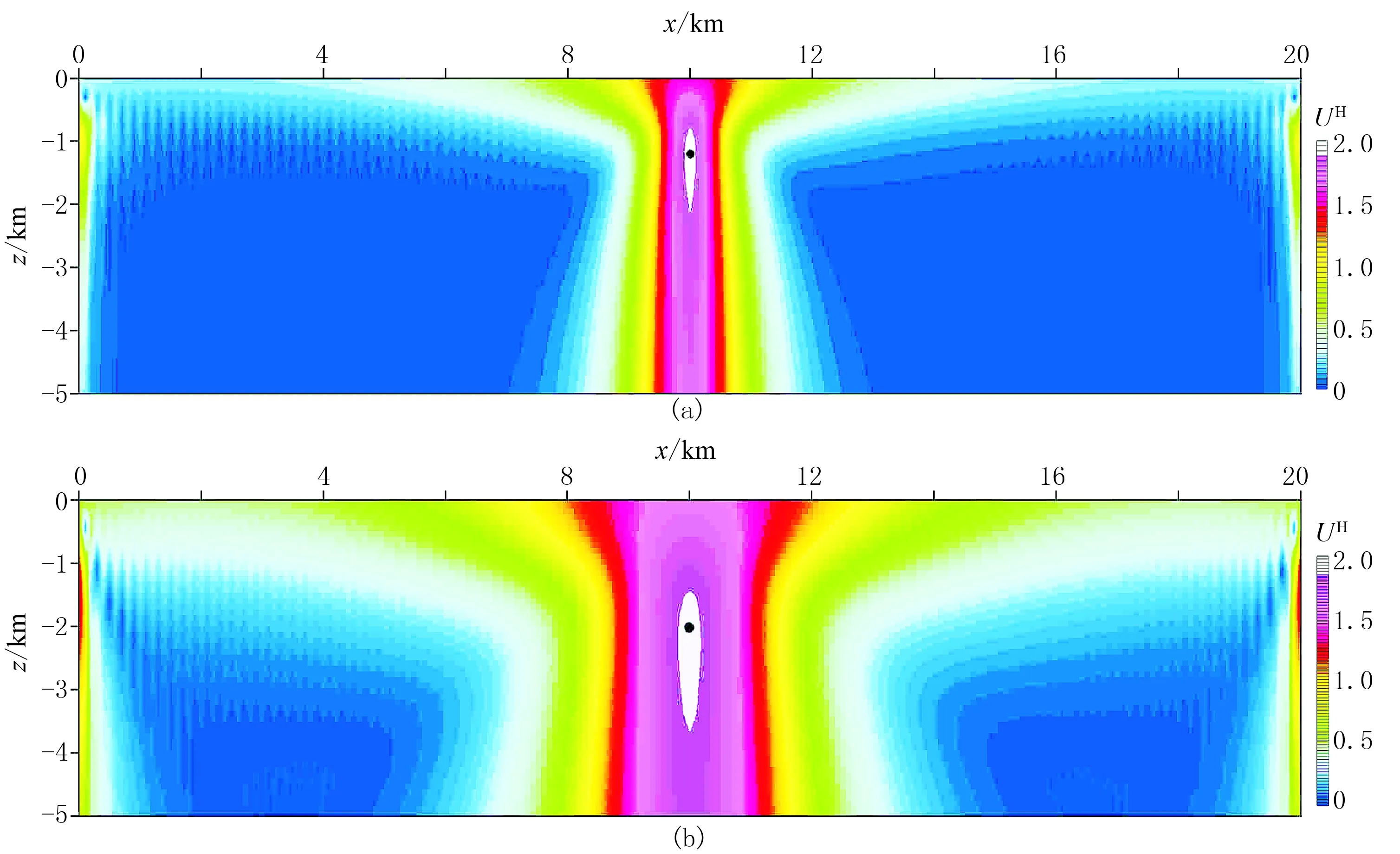
图7 台阶模型1(a)和模型2(b)磁异常幂次平均归一化总梯度场

图8 叠加模型磁异常及其解析信号(a)和模型示意图(b)

图10a是整条测线的最佳幂次数、最佳迭代次数时的磁异常归一化总梯度场，可以看出，总梯度场仅能反映岩脉的位置信息，无法有效识别台阶和水平圆柱体。依据地面磁异常解析信号(图8a)特征，将测线离散化为3段：0～16.0km、16.0～25.5km和25.5～40.0km。由于未离散化的磁异常归一化总梯度可以较好地识别出16.0～25.5km之间的磁异常体，因此该段无需再处理。图9c～图9f分别是第一段(0～16.0km)和第三段(25.5～40.0km)磁异常max(UH)及其深度值随迭代次数n和幂次数p的关系曲线。可以看出，第一段幂次数p=4与p=5时，最佳迭代次数下的max(UH) 对应的深度值一致，即该段最佳幂次数为4，与上述台阶模型试验对应的最佳幂次数一致， 对应的坐标为(10.0km，2.1km)，与台阶上顶埋深位置基本一致；第三段最佳幂次数p=1，为水平圆柱体对应的幂次数，最佳幂次数时最佳迭代次数的max(UH)对应的坐标为(30.0km，0.9km)，与理论质心坐标(30.0km，1.0km)较为接近。图10b是离散归一化总梯度场，由图可见，可以根据极值圈闭识别三个地质体的位置，有效提高了归一化总梯度法的实用性。

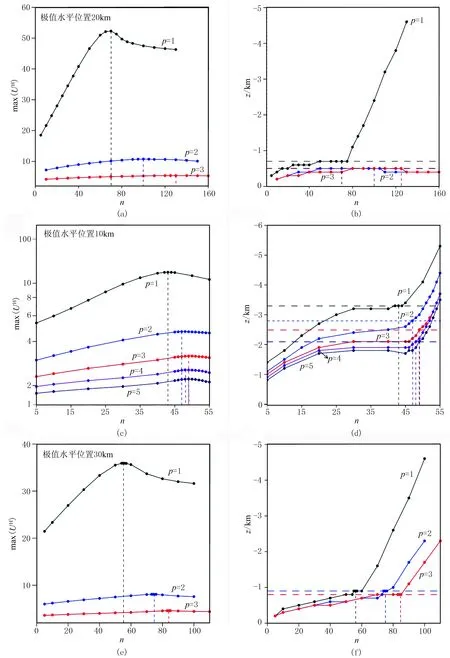
图9 叠加模型整条剖面max(UH)随p和n的变化曲线(a)、 叠加模型整条剖面max(UH)对应的深度随p和n的变化曲线(b)、 叠加模型0～16.0km的max(UH)随p和n的变化曲线(c)、 叠加模型0～16.0km的max(UH)对应的深度随p和n的变化曲线(d)、 叠加模型25.5～40.0km的max(UH)随p和n的变化曲线(e)及叠加模型25.5～40.0km的max(UH)对应的深度随p和n的变化曲线(f)

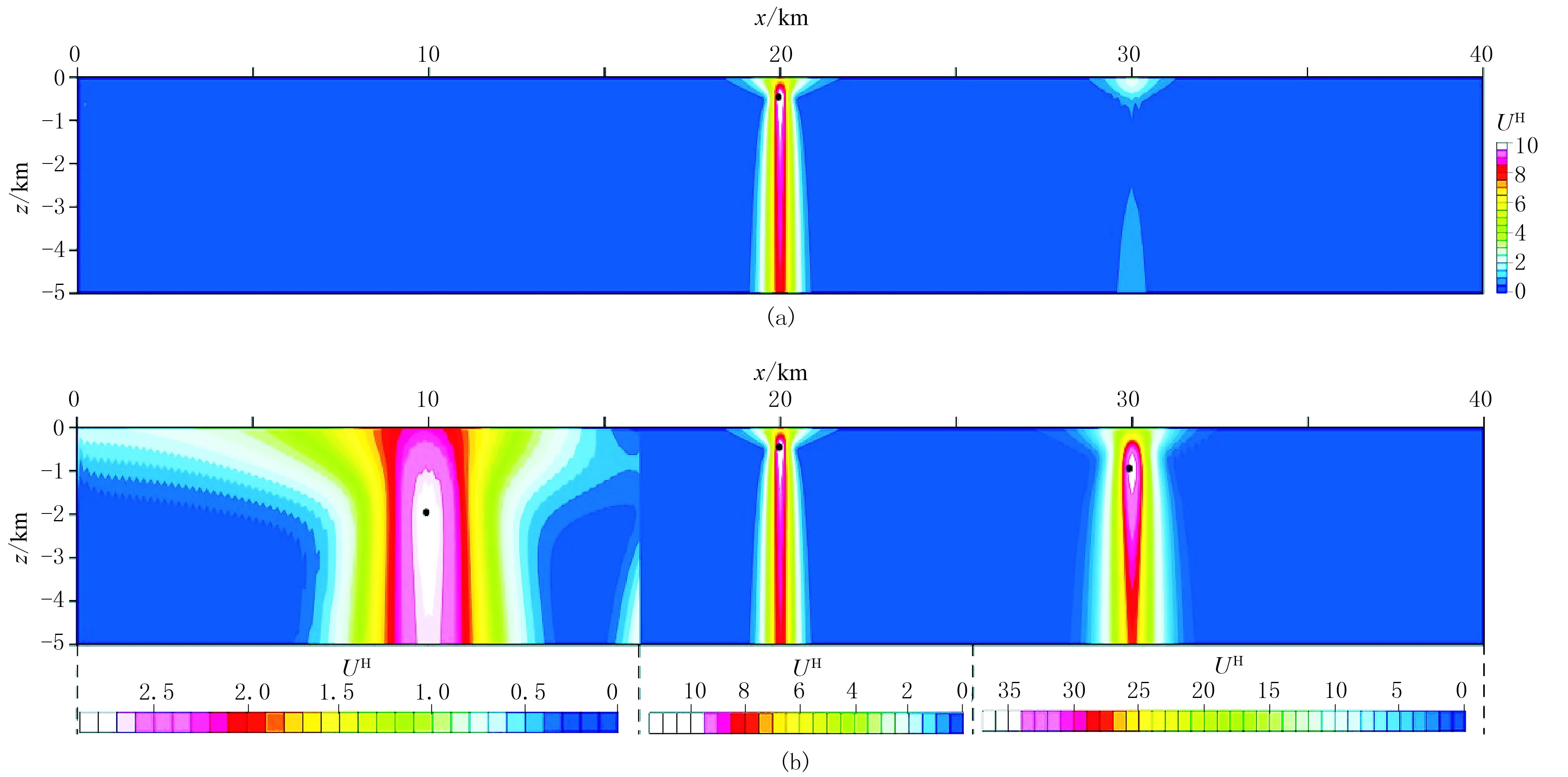
图10 叠加模型整条剖面(a)及离散剖面拼贴(b)的磁异常幂次平均归一化总梯度场

4 实例应用

为了验证基于幂次平均的离散归一化总梯度法的实用性，选取中国内蒙古某地区的地面磁异常场进行试验，研究区地表全部被沉积层所覆盖。图11是网格化为250m×50m后的磁异常图，可以看出，研究区南侧存在一条近东西走向的条带状磁异常，在西北侧还存在一个长轴近东西走向的椭圆状磁异常。为了查明这两个磁异常对应的磁源参数信息，在磁异常图中选取了两条南北走向的试验剖面AA′和BB′，对应的磁异常及解析信号曲线见图12。可以看出，AA′剖面上有两个明显的解析信号极值，推断沿这条剖面存在两个磁性体；BB′剖面上只有一个明显的解析信号极值，认为地下主要存在一个磁源体。

首先采用基于圆滑滤波因子qm(式(4))的常规归一化总梯度法对两条剖面进行处理。图13是常规归一化总梯度场极值及其深度值随谐波数N的变化曲线。可以看出，在AA′、BB′剖面上，最佳谐波数N时归一化总梯度场极值对应的深度分别为100m和400m。图14是最佳谐波数时AA′和BB'剖面磁异常的常规归一化总梯度断面图，可以看出，AA′剖面常规归一化总梯度在坐标(4000m，100m)处存在明显的极大值，分别在坐标(1800m，100m)、(3450m，100m)和(3650m，100m)处也存在极值，但极值圈闭范围较小，可能是磁性体引起的，但也可能是噪声压制不彻底导致的；BB′剖面的常规归一化总梯度在坐标(1450m，400m)处存在最大值，还在坐标(2200m，400m)、(4250m，1800m)两处存在明显的极值圈闭。

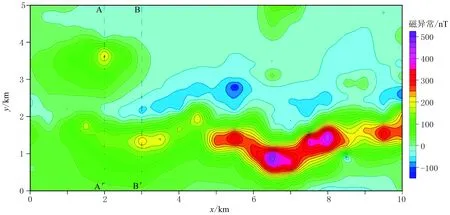
图11 中国内蒙古某地区磁异常等值线图

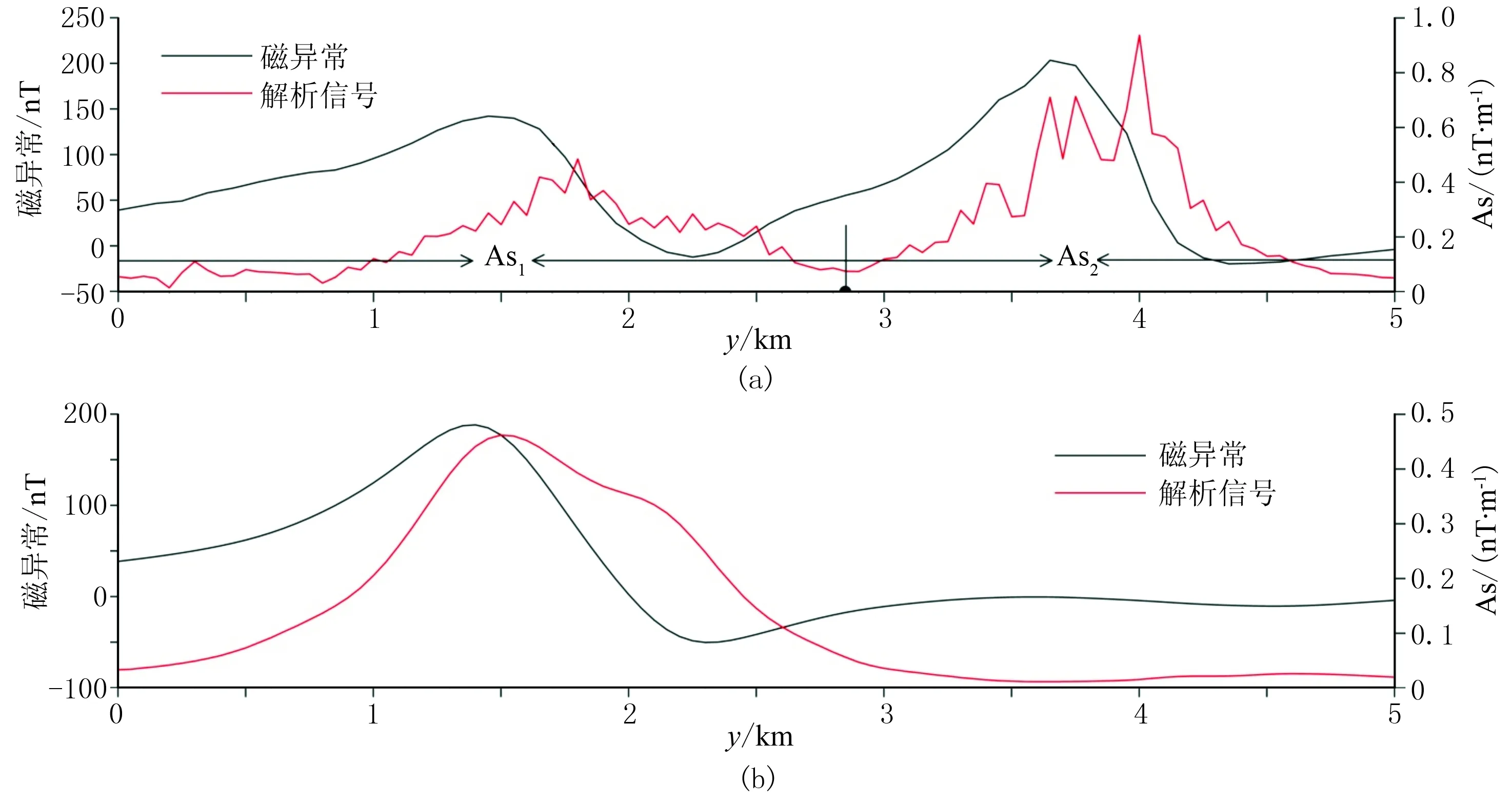
图12 图11中AA′剖面(a)和BB′剖面 (b)的磁异常及其解析信号

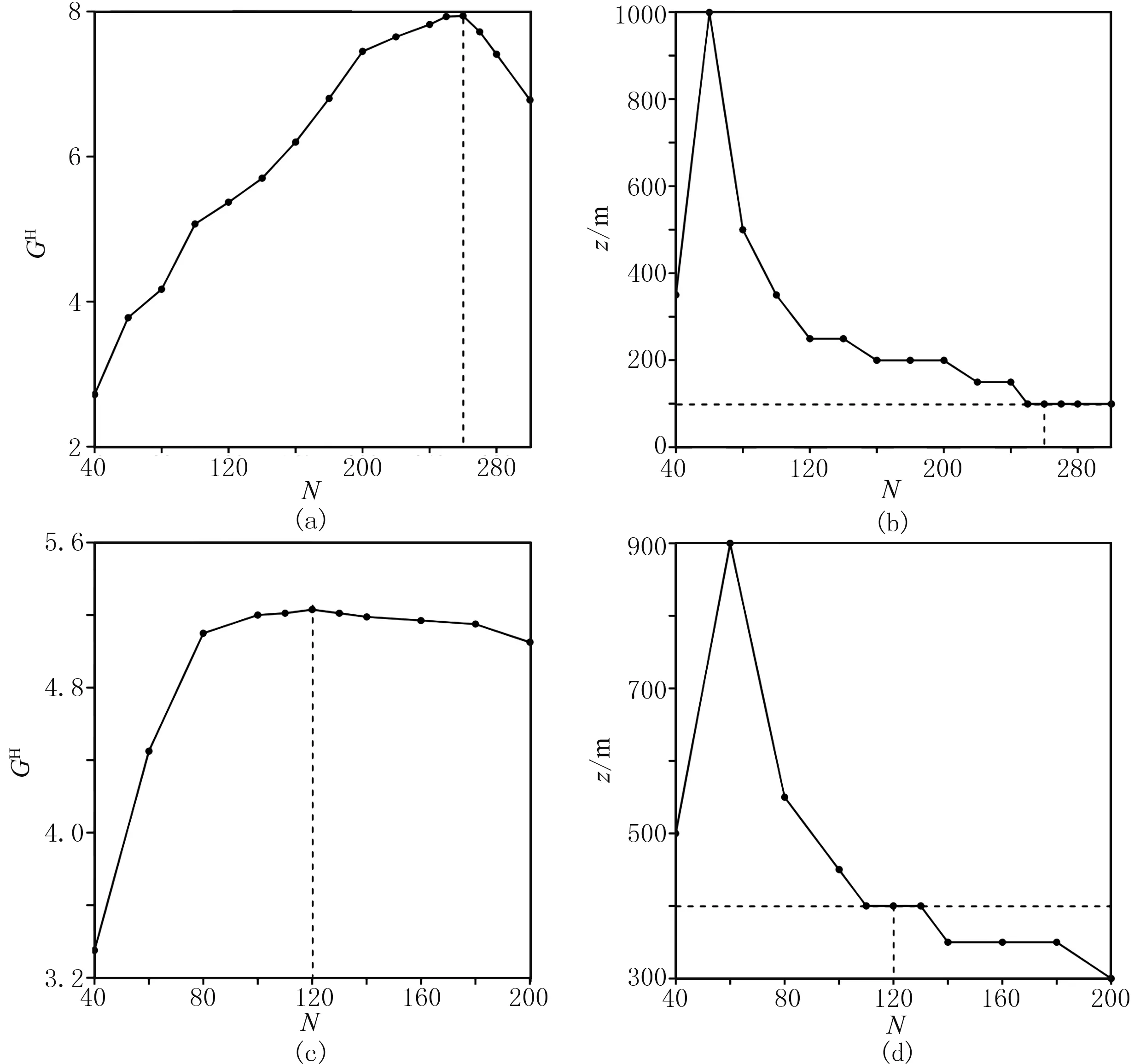
图13 常规归一化总梯度场极值及其对应的深度随谐波数N的变化曲线

(a)AA′剖面常规归一化总梯度场极大值与谐波数N的关系曲线； (b)AA′剖面常规归一化总梯度场极大值对应的深度与谐波数N的关系曲线； (c)BB′剖面常规归一化总梯度场极大值与谐波数N的关系曲线； (d)BB′剖面常规归一化总梯度场极大值对应的深度与谐波数N的关系曲线

再采用基于幂次平均的离散归一化总梯度法对两条剖面磁异常进行处理。根据AA′剖面的解析信号(图12a)，可把水平位置2850m作为离散点将测线分为两段。图15a、图15b分别是AA′剖面磁异常max(UH)及其对应的深度与幂次数和迭代次数的关系曲线；图15c、图15d分别是该剖面离散化后0～2850m的磁异常max(UH)及其对应的深度与幂次数和迭代次数的关系曲线。可以看出，水平位置4000m处的磁性体最佳幂次数p=1，推断地质体类似为水平圆柱体，该最佳幂次数下最佳迭代次数时的max(UH)对应的深度为350m；在水平位置为1800m处的磁性体最佳幂次数p=2，即可认为磁性体近似于岩脉，最佳幂次数下最佳迭代次数时的max(UH)对应的深度为550m。从BB′剖面的解析信号图(图12b)可以看出，该剖面解析信号异常主要有一个极值点，因此该剖面无需离散化。图16a、图16b分别为BB′剖面磁异常max(UH)及其对应的深度随参数p和n的变化曲线，从中可知，在水平位置1400m处地下存在一个磁性体，该磁性体的最佳幂次数p=2，即磁源接近于岩脉形状，最佳幂次数下最佳迭代次数时的max(UH)对应的深度为450m。图17a、图17b分别是AA′、BB′剖面的幂次平均离散归一化总梯度断面图，可以看出，AA′剖面的磁异常幂次平均离散归一化总梯度场在坐标(1800m，550m)和(4000m，350m)处清晰地展示出两个明显的极值圈闭，虽然常规归一化总梯度(图14a)也在水平位置1800m和4000m处存在两个极值，但极值对应的深度(均为100m)与改进方法获得的深度存在较大偏差。BB′剖面的磁异常幂次平均归一化总梯度场在坐标(1400m，450m)处存在一个明显的极值圈闭，在坐标(2200m，400m)也存在一个极值圈闭，可能在该处也存在一个磁性体，只是地表磁异常解析信号分辨率不够高导致未被识别；常规归一化总梯度(图14b)在水平位置1400m和2200m处识别的磁性体埋深均为400m，与改进方法计算结果基本一致。

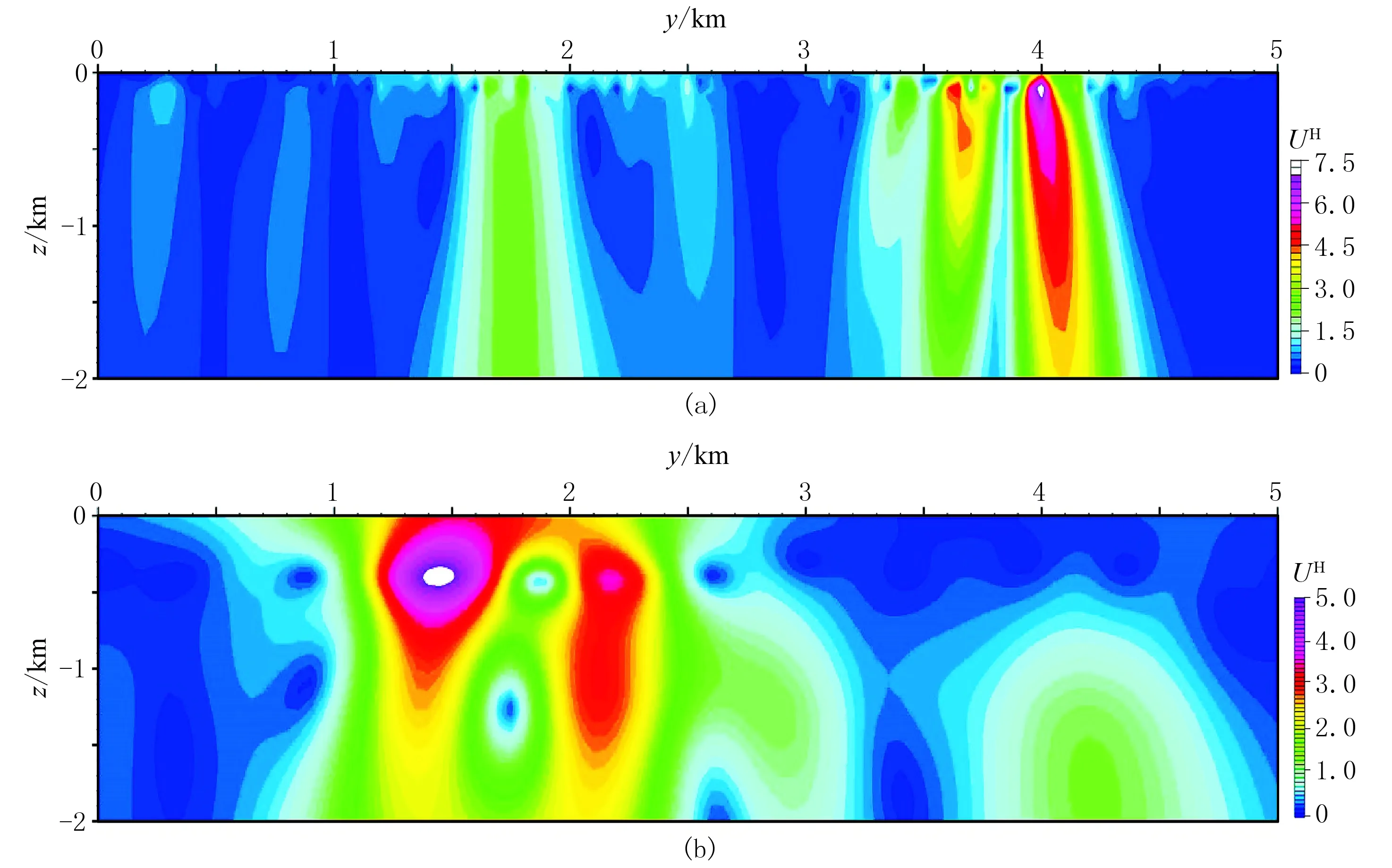
图14 AA′(a)、BB′(b)剖面磁异常常规归一化总梯度场

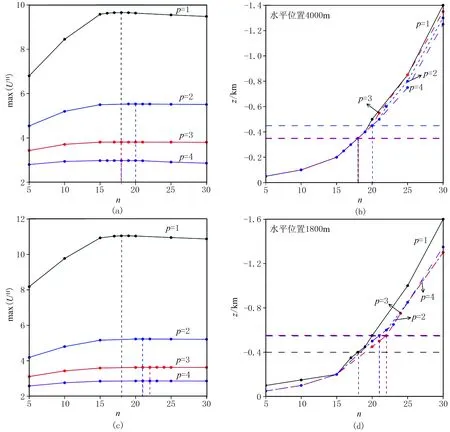
图15 AA′剖面max(UH)随p和n的变化曲线(a)、 AA′剖面max(UH)对应的深度随p和n的变化曲线(b)、 AA′剖面0～2850m磁异常max(UH)随p和n的变化曲线(c)及AA′剖面0～2850m磁异常max(UH)对应的深度随p和n的变化曲线(d)

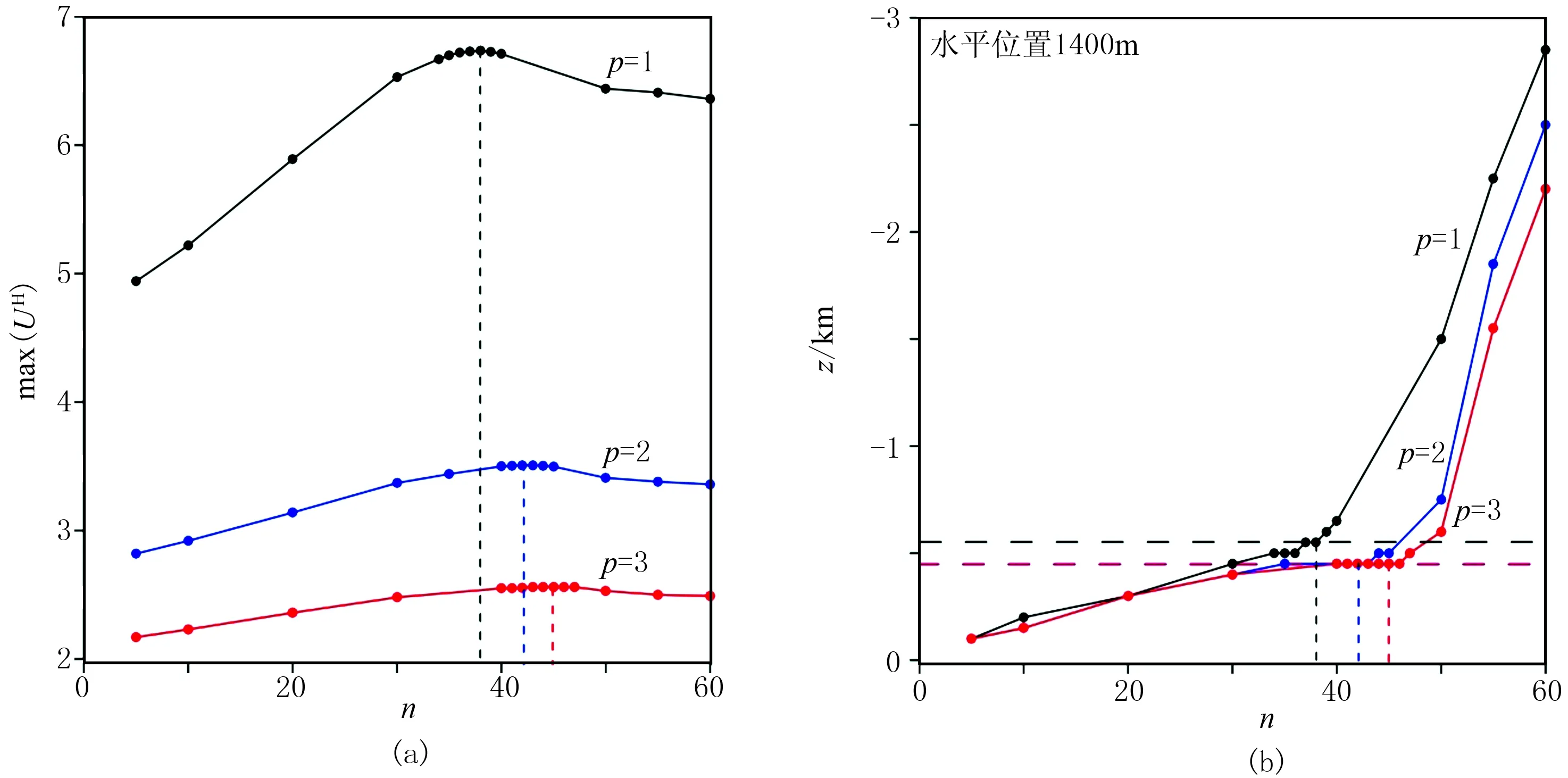
图16 BB′剖面max(UH) 随参数p和n的变化曲线(a)及max(UH)对应的深度随参数p和n的变化曲线(b)

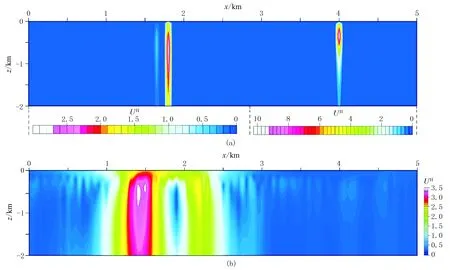
图17 AA′(a)、BB′(b)剖面基于幂次平均的磁异常离散归一化总梯度

由于没有其他地质、钻孔等已知资料验证上述结果，这里采用了磁法数据处理中常用的AN-EUL反褶积法对AA′、BB′两条剖面进行相应处理，结果分别见图18和图19。从图18可以看出，利用AN-EUL反褶积反演AA′剖面磁数据得到了两个磁性体，坐标分别为(1727.1m，543.8m)、(3839.2m，350.1m)，与幂次平均离散归一化总梯度法反演的位置基本一致；AN-EUL反褶积在上述两处反演得到的构造指数分别为1.1和1.7，即两处的磁性体分别接近于岩脉(理论构造指数为1)和水平圆柱体(理论构造指数为2)，同样与幂次平均离散归一化总梯度法估计的地质体类型相一致。从图19中可以看出，利用AN-EUL反褶积反演BB′剖面，在坐标(1524.6m，480.3m)处反演得到一个类似岩脉的磁性体(反演的构造指数为1.1)，反演结果与幂次平均归一化总梯度得到的磁性体参数同样吻合较好，这进一步证实了幂次平均离散归一化总梯度法的有效性和实用性。

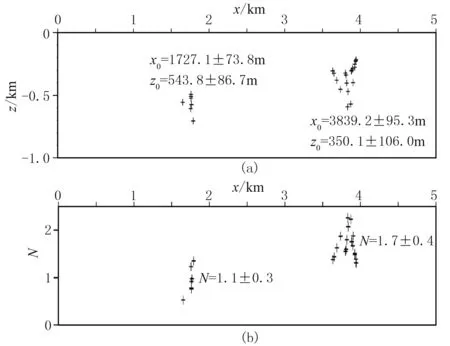
图18 AA′剖面磁异常AN-EUL反演结果(a)位置解; (b)构造指数解

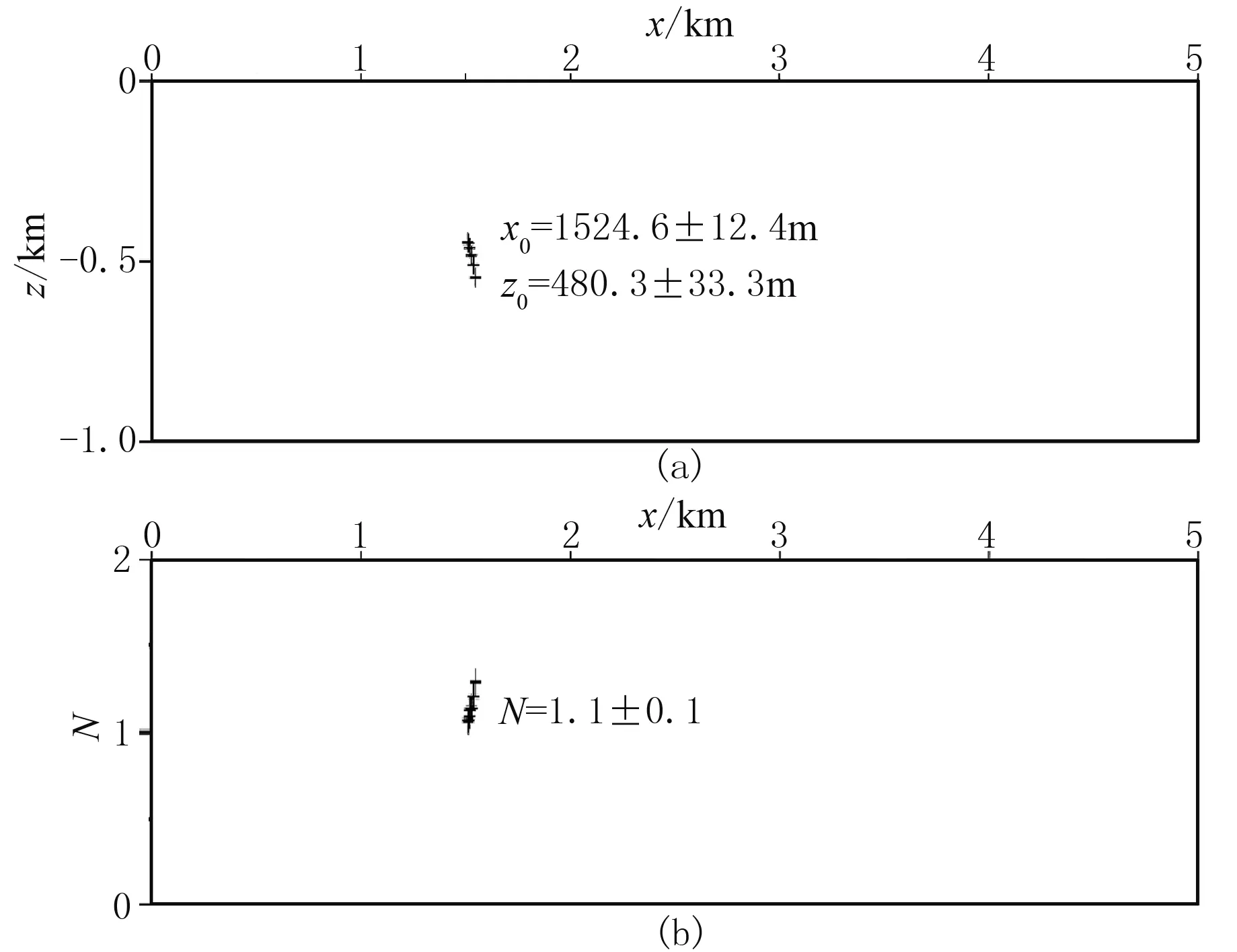
图19 BB′剖面磁异常AN-EUL反演结果(a)位置解; (b)构造指数解

5 结论

本文在分析常规归一化总梯度法的优缺点基础上，利用迭代滤波法代替圆滑滤波实现稳定向下延拓，采用幂次平均替换算术平均进行归一化计算，并对归一化总梯度场进行离散化处理，由此推导出了基于幂次平均的离散归一化总梯度法。模型试验证实，基于幂次平均的离散归一化总梯度法可以用于处理叠加异常场，能够有效地识别地质体的位置及几何形状参数。实例应用表明，相对于常规归一化总梯度法，新方法不仅可以有效地反映叠加异常的场源分布，获得更高的反演精度，还可以推断地质体的几何形状特征，有效提高归一化总梯度法的地质解释能力。