地震射线追踪的线性走时扰动插值法

李同宇 张建中

(①海底科学与探测技术教育部重点实验室，山东青岛 266100； ②青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266061； ③中国海洋大学海洋地球科学学院，山东青岛 266100)

1 引言

地震射线追踪及走时计算是地震学的基本问题之一，被应用于层析成像、地震定位、偏移以及地震数据采集设计等领域[1，2]。传统的射线追踪方法主要针对两点射线追踪问题，可分为试射法[3]和弯曲法[4]。这两种方法都存在一定局限性： 前者需不断试验射线入射角，计算效率较低； 后者易于陷入局部最优解。20世纪80年代后期，出现了基于地震波前走时的射线追踪方法，如程函方程的有限差分法[5-8]、最短路径法[9-13]和线性插值算法[14-24]等。与传统方法相比，该类方法具有较高计算精度和效率，得到广泛研究和应用。

Asakawa等[14]提出基于线性插值的二维走时计算和射线追踪方法(LTI)，指出由于可通过对LTI求导得到程函方程有限差分[5]公式，因而LTI方法可被视作程函方程有限差分法的更高版本，并对比说明了LTI方法具有更高的计算精度和效率。但是，LTI算法从震源开始逐步向外围推进的过程中，考虑的波传播方向有限，计算的节点处走时不一定是最小走时，也不能正确追踪逆向传播的射线。为了克服这些问题，该方法被不断的修正和改进。张建中等[15，16]结合LTI与最短路径算法，提出了动态网络射线追踪方法。黄月琴等[17]将二维LTI算法推广至三维情形。Zhang等[18]结合双线性走时插值和波前扩展法，提出了基于规则单元的三维射线追踪方法，随后Huang等[19]将该方法推广至适用于不规则六面体单元。李培明等[20]提出了一种改进的双线性插值射线追踪方法，并结合动态变密度网格剖分，提高了旅行时的计算精度和效率。黄翼坚等[21]通过对传统初至波LTI算法的射线方向进行约束，得到了一种直达波旅行时LTI迭代算法。张东等[22]通过使用LTI计算向前过程的离散旅行时场，并用B样条插值梯度反向追踪射线路径，提出了初至波走时梯度射线追踪算法(MTG)，较大程度消除了计算网格离散化带来的误差。在此基础上，张婷婷等[23]结合逐次网格剖分技术及MTG方法，实现了三维层状介质中的多波走时计算及射线追踪，随后针对在速度突变区域用B样条插值计算旅行时梯度会带来误差的问题，张婷婷等[24]在三维MTG射线追踪算法基础上提出了一种改进的B样条/线性联合插值的三维射线追踪(MMTG)算法。

LTI方法假设地震走时沿单元边界线性变化，单元边界上任意一点的走时可由该边界上已知点走时的线性插值函数表示。但实际上，单元边界上的走时呈非线性变化，因而当离散单元较大时，LTI方法的线性假设会导致较大的走时计算和射线追踪误差。针对这一问题，Zhang等[25]提出了基于规则单元的线性走时扰动插值(LTPI)方法，提高了波前走时的计算精度。为了更好模拟地形和地层界面的起伏及各地层速度的变化，本文将复杂介质模型离散成不规则单元，推导了二维情况下适用于不规则单元的LTPI方程，并结合波前扩展算法，提出了一种基于线性走时扰动插值的射线追踪方法，数值实验证明该方法具有较高的计算精度、效率以及很强的对复杂介质的适应性。

2 方法原理

基于LTPI的射线追踪算法包括两步：波前走时计算和射线追踪。在波前走时计算过程中，根据惠更斯原理，结合群波前扩展算法(GMM)和LTPI方法，从震源开始逐步向外计算离散模型中各网格节点的波前走时；追踪射线时，根据费马原理，从接收点开始反向逐步确定射线与相关单元边界的交点，直至追踪至炮点，将炮点、各个交点和接收点顺次连接，则得到从炮点到接收点的射线路径。

2.1 模型离散

为模拟地形与地层界面的起伏，复杂模型被离散成如图1所示的一系列不规则四边形单元[19]。具体离散过程如下。

首先，在x方向等间距剖分模型。记模型在x方向的起始坐标为xc，剖分间距为Δx，剖分网格数目为n。离散模型的横坐标可表示为

x(i)=xc+iΔxi=0，1,2,…，n

(1)

然后，由浅至深分别将每个地层划分成多个薄层。在同一地层中，薄层数目相等，并且在同一x坐标处，各薄层在z方向上的厚度相等。不同地层的薄层数目可以不同。假设第k个地层中划分的薄层数目为dk，则第k个地层中的第m个薄层在x=x(i)处的底面深度值可表示为

(2)

式中lk(i)和lk+1(i)分别表示第k个地层的顶面和底面在x=x(i)处的深度值。

这种离散方式可很好地拟合起伏地形和地层界面，不仅考虑了每个地层内速度的纵向和横向变化以及地层速度与界面的耦合问题，且易于自动实现。

2.2 基于走时扰动插值的走时计算

在波前走时计算过程中，需计算与各级震源点相邻的网格节点处的波传播时间，即在一个单元内由已知节点走时计算未知节点走时。在单元较大时，LTI方法的线性走时假设会导致较大的计算误差，因此本文引入线性走时扰动插值(LTPI)方法[25]，并将它扩展到适于不规则单元的情况。

在图2中，假设射线穿过不规则单元的上顶边界。S点表示震源点，P1和P2为单元上顶边界两个走时已知节点，坐标分别为(xi，zi)(i=1，2)，其波前走时分别为t1和t2。需计算射线从震源点S穿过单元上顶边界传至该单元边界节点E的走时。

设从震源传至E点的射线与单元上顶边界的交点为P点，设上顶边界的中点为P0(x0，z0)，P点坐标可表示为

(3)

式中：r为P点与P0点横坐标之差，当P点在P0点右侧时r大于零，否则r小于零；a0为常数，有

(4)

若P点走时为tP，则E点走时tE可表示为

tE=tP+slPE

(5)

式中：lPE表示P点至E点的射线长度；s表示该单元内的平均慢度。

现在采用LTPI方法[25]计算P点走时和坐标。将图2中震源点S至单元上顶边界之间的介质等效成匀速介质。在等效匀速介质中，从S点至单元上顶边界的射线路径为直线。若S点至P1、P2点的直线长度分别为l1、l2，则等效匀速介质的平均慢度seq可表示为

(6)

由此可求得等效匀速介质中从震源点S至点Pi(i=1，2)的射线走时为

(7)

Δti=ti-seqlii=1,2

(8)

对于均匀模型，等效介质射线与实际射线重合，走时扰动为零。对于非均匀模型，等效匀速介质中的直射线与实际射线不同，走时扰动一般为非零值，且远小于参考走时。

据式(6)～式(8)，P点处走时扰动可表示为

ΔtP=tP-seqlSP

(9)

式中lSP为等效匀速介质中S点至P点的射线长度。将式(9)代入式(5)，S点至E点的走时可表示为

tE=ΔtP+seqlSP+slPE

(10)

式中P点处的波前走时被分解为参考走时seqlSP和走时扰动ΔtP。其中参考走时由定义求得，而ΔtP可由单元边界上已知点的走时扰动表示。

假定走时扰动沿单元边界线性变化，P点的走时扰动ΔtP可用线性方程表示为

ΔtP=ar+b

(11)

式中a和b为常系数，可由P1和P2点处的已知走时扰动Δt1和Δt2表示

(12)

设炮点S坐标为(xS，zS)，E点坐标为(xE，zE)，据式(3)有

(13)

为简化计算， 将lSP=f1(r)和lPE=f2(r)在r=0处分别进行泰勒级数展开，保留至二次方项，并把f1(0)和f2(0)分别简化记为f1和f2，则有

(14)

其中

将式(6)、式(11)和式(14)代入式(10)中，由费马原理可知，E点的波前走时满足公式

(15)

求解式(15)可得

(16)

其中

由式(16)求得r值后，根据式(3)可知射线与单元上顶边界的交点P的坐标，将r代入式(10)即可求得射线经过单元上顶边界到达E点的走时。射线穿过单元其他边界时的走时计算方法与此类似。

若不规则单元的其他边界节点的走时也已知，同样也可用上述方法求出射线穿过其他边界到达E点的走时，然后将各个走时中的最小者作为所求E点处的波前走时。

2.3 波前扩展

本文采用群波前扩展算法(GMM)扩展波前。复杂介质离散后，每一个单元都被认为是均匀的，射线在单元内沿直线传播。波前扩展的二维情形如图1 所示。从震源点开始，利用LTPI计算出与其相邻的各个网格节点上的波传播时间，这些节点组成波前窄带。在波前窄带中需要按照一定规则找出次级震源点，再从次级震源点处开始计算与其相邻的网格节点处的波传播时间，这些网格节点便组成了新的波前窄带[19]。波前窄带需要不断向外推进直至获得介质中全部网格节点处的波前走时。

记当前波前窄带为N，令

(17)

式中：sN，min表示波前窄带各个网格节点中波传播的最小慢度，即最大波传播速度； Δx和Δz为波前窄带各网格在x和z方向上的离散网格距。

由GMM算法可知若波前窄带中两个相邻网格节点的波传播时间之差小于δtN，则这两点处的波传播能量不会互相影响。次级震源集合G的选择需遵循如下规则

G={(i,j)∈N,ti,j≤tN,min+δtN}

(18)

式中tN,min表示波前窄带N中的最小波传播时间。

波前走时计算步骤如下：

(1)将震源点的波前走时记为0，并且记M=2，表示该处已获得波前走时； 其余网格节点的波前时间均记为无穷大，并令其M=0，表示该网格节点未计算波前走时；

(2)计算与震源相邻的网格节点处的波的传播时间后，将时间保存到波前窄带N中，并令M=1，表示该处网格节点已计算出波传播时间，但还未确定波前时间；

(3)波前窄带中满足式(18)的网格节点处的波传播能量不会相互干扰，因此将其作为次级震源，将满足条件的网格节点从波前窄带N中移至次级震源集合G中，并令M=2；

(4)对次级震源集合G中的网格节点，更新与其相邻的网格节点处波传播时间，要注意相邻网格节点需满足M≠2，若节点处M=0，则将该节点移至波前窄带N中并令M=1；

(5)若集合N非空，则跳转至步骤(3)；若集合N为空，则波前扩展结束。

2.4 射线追踪

在计算出复杂介质全部网格节点处的波前走时后，根据费马原理和互换原理，可从接收点出发反向逐步确定出射线与相应单元边界的交点，直至追踪至炮点； 然后顺次连接该对炮点和接收点之间确定的所有交点，便得到具有最小走时的直达波射线路径。具体射线追踪步骤如下。

(1)在接收点R所在单元内，利用LTPI方法计算射线路径与该单元各边界的交点P(图3)。若接收点位于单元节点或单元边界上，则需要在接收点所在的所有单元中进行计算。

(2)将具有最小走时的交点P作为新的接收点，判断接收点是否位于炮点所在单元，若是，执行步骤(3)； 否则返回步骤(1)。

(3)顺次连接炮点、射线与相应单元边界的各个交点和接收点，就得到了该对炮点和接收点对应的直达波射线路径。

图3 一个单元内射线路径追踪示意图

3 数值实验

为测试本文方法，设计了四种模型：均匀介质速度模型(模型1)、垂向渐变速度模型(模型2)、倾斜层状速度模型(模型3)和含异常体速度模型(模型4)。前两种模型的波前走时和射线路径有解析解，可使用均方根误差

(19)

3.1 均匀介质速度模型

模型1是尺寸为2000m×2000m的均匀介质速度模型，离散为一系列80m×80m的规则单元。模型速度为4000m/s，震源坐标为(0，1000m)。图4a和图4b分别为用LTI和LTPI方法计算得到的波前走时(红色虚线)与理论值(灰色实线)的对比图，用相应方法计算的波前走时与理论值之间的绝对误差分布分别如图4c和图4d所示。可见LTPI方法计算的波前走时更接近理论值，绝对误差更小。

图4 模型1波前走时等值线(单位：ms)及绝对误差(a)LTI方法走时； (b)LTPI方法走时； (c)LTI方法误差； (d)LTPI方法误差

为说明计算误差和计算时间随离散单元大小的变化，对模型1分别以10、20、40、50、80、100和200m的网格尺寸进行离散，然后计算了LTI和LTPI方法的波前走时均方根误差，并记录了CPU时间(图5)。可见在相同离散网格距下，LTI和LTPI方法所用CPU时间相近，而LTPI方法的均方根误差值要远小于LTI方法。随着网格距的增大，LTI方法的均方根误差值增长迅速，而LTPI方法的均方根误差值则变化较为平缓。因此在一定误差要求下，LTPI方法可以使用比LTI方法更少的单元数目，从而提高计算效率。

将模型1以80m的网格尺寸进行离散，分别使用LTI和LTPI方法计算射线路径，与理论路径的对比如图6a和图6b所示。使用相应方法计算的各个接收点对应的射线走时及其相对误差对比分别如图6c和图6d所示。相比LTI方法，LTPI方法计算的射线路径和射线走时更接近理论值。在不同接收点处使用LTPI方法得到的走时相对误差稳定在1.0×10-3附近，小于LTI方法对应的误差值。可见，LTPI方法具有更高的计算精度。

图5 LTI和LTPI方法在不同离散网格距下的均方根误差和CPU时间

3.2 垂向渐变速度模型

速度随深度线性变化介质的波前走时和射线路径具有解析解[26]。为将本文方法结果与变速介质的理论值进行对比，建立了速度随深度线性增加的模型2，其尺寸为2000m×2000m，离散网格尺寸为40m×40m，速度随深度线性变化函数为v=1500+2z(深度单位为m，速度单位为m/s)。炮点位于(1000m，0)。图7a和图7b分别为用LTI和LTPI方法计算出的波前走时(红虚线)与理论值(灰实线)的对比图，图7c和图7d分别是用相应方法计算的波前走时绝对误差分布图。可见LTPI方法比LTI方法计算的波前走时更贴近理论值，计算精度更高。

图6 模型1的射线路径及走时对比图(a)LTI方法射线； (b)LTPI方法射线； (c)计算走时与理论走时； (d)计算走时相对误差

图7 模型2波前走时等值线(单位：ms)和绝对误差分布图(a)LTI方法走时； (b)LTPI方法走时； (c)LTI方法误差； (d)LTPI方法误差

为说明本文方法对离散单元大小的响应，将模型2分别以10、20、40、50、80、100和200m网格尺寸做离散，分别用LTI和LTPI方法计算波前走时均方根误差并记录了CPU时间(图8)。可见在同一网格距下，LTI与LTPI方法所用的CPU时间相近，但LTI方法的均方根误差比LTPI方法大一倍以上。随着网格距的增大，LTI方法的均方根误差值快速增大，而LTPI方法的均方根误差值变化相对平缓。因此在一定误差要求下，LTPI方法可使用比LTI方法更少的单元数目以提高计算效率。

将模型2以40m的网格尺寸离散，炮点坐标为(1000m，2000m)，图9a和图9b分别为使用LTI和LTPI方法计算的射线路径与理论路径的对比图，不同接收点处分别使用这两种方法得到的射线走时及其相对误差分别如图9c和图9d所示。可见在速度随深度线性增加的模型中，使用LTPI方法得到的射线路径和射线走时更加贴近理论值，并且对应的走时相对误差要小于LTI方法。

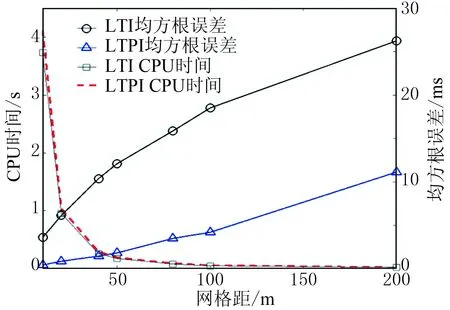
图8 不同网格距下LTI和LTPI方法计算的均方根误差和CPU时间

图9 模型2中射线路径及走时对比图(a)LTI方法射线； (b)LTPI方法射线； (c)计算走时与理论走时； (d)计算走时相对误差

3.3 倾斜层状速度模型

模型3由三层倾斜层状介质组成，各层速度从上到下分别为2000、3000和4000m/s。模型尺寸为2000m×2000m，震源位于(1000m，0)。分别使用LTI和LTPI方法计算离散网格距为20m(灰色实线)和80m(红色虚线)时的波前走时(图10)。可见离散网格尺寸变化时，使用LTPI方法得到的波前走时更加一致，与LTI方法相比，LTPI方法具有良好的稳定性，能更好地适应大网格距离散模型。

用网格距为40m的网格离散模型3。为获取倾斜层状介质中的理论射线路径，先设定炮点位置为(1000m，1800m)，再从炮点处以一定的出射角出射射线，根据Snell定律确定射线路径，将射线在地表的出射点作为接收点。然后分别使用LTI和LTPI方法计算了这些炮检点所对应的射线路径(图11a和图11b所示)。可见用LTPI方法计算的射线路径更接近理论射线路径。不同接收点处对应的射线走时及其相对误差分别如图11c和图11d所示，使用LTPI方法计算得到的走时相对误差稳定在1.0×10-3以下，小于LTI方法的相对误差。实验结果说明LTPI方法比LTI方法具有更高的计算精度。

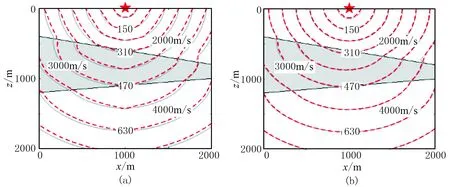
图10 离散网格距分别为20m和80m时，模型3波前走时等值线图(单位ms)(a)LTI方法； (b)LTPI方法

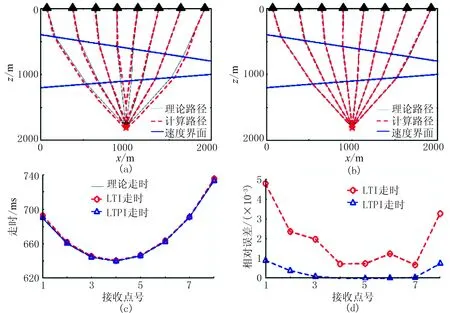
图11 模型3中射线路径与走时对比图(a)LTI方法射线； (b)LTPI方法射线； (c)计算走时与理论走时； (d)计算走时相对误差

3.4 含异常体速度模型

模型4尺寸为2000m×2000m，由三层起伏层状介质组成，从上到下速度分别为1700、2800和1800m/s。在上层介质中存在速度为2100m/s的高速体，中间层介质含一速度为2300m/s的低速体。震源位于(1000m，2000m)。分别用LTI和LTPI方法计算了离散网格距为20m(灰色实线)和80m(红色虚线)时波前走时(图12)。可见两种方法计算的波前走时趋势基本一致，反映出遇到低速体、高速体和地层界面时的波前变化特征。相比LTI方法，LTPI方法在网格距增大时走时变化更小，稳定性更高。

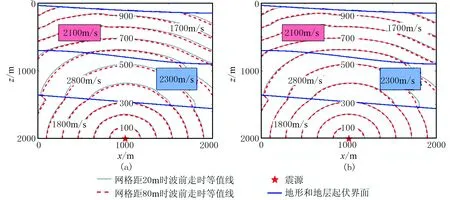
图12 离散网格距分别为20m和80m时模型4波前走时等值线(单位ms)图(a)LTI方法波前走时； (b)LTPI方法波前走时

将模型4分别用20m和80m的网格距离散，并分别使用LTI和LTPI方法计算射线路径(图13)。可见LTI和LTPI两种方法计算的射线路径都表现出尽量避开低速体和趋向高速体的特征。但是，当模型离散网格距发生变化时，LTI方法计算的射线路径变化较大，而LTPI方法计算得到的射线路径更为合理且变化更小，反映出LTPI方法更具优势。

图13 模型4射线路径图(a)LTI方法； (b)LTPI方法

4 结论

线性走时扰动插值(LTPI)方法将实际波前走时分解为等效匀速介质中的参考走时与走时扰动。参考走时沿单元边界非线性变化，虽然假设走时扰动在单元边界上线性变化，但与参考走时相比，走时扰动很小。因此，参考走时与走时扰动之和仍保持着沿单元边界非线性变化的特征，从而克服了常用的线性走时插值(LTI)方法在离散单元较大时计算走时误差大的问题，提高了波前走时的计算精度。

采用不规则单元离散复杂介质模型，能够更好地模拟地形和地层界面的起伏形态以及各地层内速度的纵横向变化。针对不规则单元，建立了基于LTPI的走时计算方程，并结合GMM波前扩展算法，提出了一种基于线性走时扰动插值的射线追踪方法，对复杂介质模型具有很强的适应性。

不同模型的测试结果表明， 相比LTI方法，LTPI方法在波前走时和射线路径方面具有更高的计算精度，并且随着离散模型单元尺寸的增加，LTPI方法的计算误差增加更为缓慢。在离散单元数目相同的情况下，LTPI与LTI方法的计算效率相当，但LTPI的计算精度比LTI方法高出一倍以上；在一定精度要求下，LTPI方法可使用离散单元数目更少的模型，从而提高计算效率。