多先验信息约束的三维电阻率反演方法

郭来功 戴广龙 杨本才 薛俊华 陈本良

(①安徽理工大学电信学院，安徽淮南 232001； ②安徽理工大学能源学院，安徽淮南 232001；③深部煤炭开采与环境保护国家重点实验室，安徽淮南 232001)

1 引言

直流电法是一种重要的地球物理勘探方法，在矿井突水、地质滑坡、隧道施工等岩土工程领域，地下水勘探、环境地质监测等环境工程领域，以及矿产资源调查等资源勘探领域均有广泛应用[1-3]。直流电法三维成像存在固有的多解性问题，会出现异常体定位不准确的现象。另外，反演数据量大、求解效率不高，其在时效性要求较高的应用中易受到限制，因此提高反演精度和计算效率是直流电三维勘探需要解决的主要问题[4,5]。

在三维反演中引入更多的先验信息进行约束，是提高成像效果的主要手段之一。刘征宇等[6]提出几种有效方法，一是引入距离加权约束，构建距离加权因子分布模型，对于不同的电源点距离，施加指数规律的权重因子，对不同单元赋予差异权重，反演的异常体形态得到有效改善；二是引入不等式约束，将介质电阻率的取值范围作为先验约束条件，提高反演精度[7]；三是引入参考模型约束，将已经获取的异常体结构信息作为先验信息施加到约束条件中，有效去除反演成像中的假异常[8]。刘鑫明等[9]采用光滑约束构造三维反演函数中的粗糙度矩阵，采用合理的网格剖分，在注浆检测中取得良好的效果。吴小平等[10]采用不完全Gauss-Newton法，应用非结构网格实现任意偶极—偶极视电阻率的三维反演，较好地展现了地下真实电阻率结构。Johnson等[11]在正演建模时通过埋设导电件，建立精准模型，提高反演成像效果。Johnson 等[12]还采用并行分布式计算方法，提高了反演效率。Farquharson[13]针对最小构造反演，提出一种分段常数的地质模型构造方法，采用L1范数准则下的迭代重加权最小二乘方法，成像结果与实际地质结构高度接近。在反演方法上，基于全局优化的模拟退火方法、人工神经网络方法等受到计算机计算能力的限制，目前还无法全面应用到实践，当前的工程应用以基于最小二乘准则的线性反演为主[14-18]。

实际应用中，仍有诸多问题需要解决。关于反演算法，当目标函数确定后，先验信息无法灵活地施加到约束中，例如引入距离加权约束后，无法再施加不等式约束信息；另外，反演耗时过长，普通计算机无法实现快速反演。本文采用分布式并行计算方法[19]，在最小二乘准则的基础上，在重加权函数中增加结构度量、权重均值和标准偏差等参数，对模型的目标区域施加不同约束，并通过合成数据进行直流电三维反演算例分析。

2 目标函数的建立

三维有限元模型空间中，模型参数用向量m表示，模型响应为f，测量数据用列向量d表示。反演过程中，网格固定不变，其目的是确定模型参数。反演通过构造一个包含模型参数和测量数据的目标函数，使其最小化。根据Farquharson[13]提出的一般准则，目标函数Φ可表示为

Φ=Φd(ud)+βΦm(um)

(1)

式中：下标“m”和“d”分别代表模型和数据；Φd(ud)是度量模型响应数据与测量数据d之间拟合差的函数；Φm(um)是度量模型参数变化的函数；β是正则化参数，控制拟合数据和模型向量变化对目标函数的影响。其中ud的表达式为

ud=Wd(d-f)

(2)

式中Wd是数据加权对角矩阵，其元素是测量数据中误差(噪声)的标准偏差σi的倒数，即1/σi。如果测量时没有考虑误差，则需对误差做合理的估计[20]。假设误差由测量电压误差ΔU和一个固定百分比误差(q%)构成，则第i个数据的标准偏差为

(3)

式中：Ui为第i个测量电压； ΔUi为第i个数据的测量电压误差。目标函数Φ中模型参数向量um可写作

um=Wm(m-mref)

(4)

式中：Wm是模型参数权重矩阵；mref表示参考模型。在一种简单的情况下，考虑三维空间的各向异性，有

(5)

式中：Cx、Cy和Cz分别是x、y、z方向的平滑矩阵；αx、αy和αz分别是x、y、z方向的相对权重。平滑矩阵C的一般形式是一阶差分矩阵[21]。

3 基于迭代重加权最小二乘法的三维反演

采用最小二乘法时，反演方程的求解采用将非线性问题线性化的方法，经过多次迭代修正模型参数，使估计解不断逼近真实解。迭代重加权的核心思想是通过计算一系列权系数并不断更新，得到目标函数的最优解。假设在第n次迭代时，得到最佳参数模型m(n)，使目标函数最小化。由式(1)，第n次迭代的目标函数可以表示为

(6)

设模型参数向量的变化量为Δm=m(n)-m(n-1)，则第n次迭代时，得到模型m(n-1)的正演结果

f(n)≈f(n-1)+JΔm

(7)

式中J为偏导数的灵敏度雅克比矩阵，其元素为

(8)

表示第j个模型参数的变化导致的第i个模型响应的变化，因此，由式(2)和式(4)可得

ud=Wd[d-f(n-1)-JΔm]

(9)

um=Wm[m(n-1)+Δm-mref]

(10)

式(6)是关于Δm的函数，最小化式(6)，令其偏导为零，结合式(9)、式(10)，应用Gauss-Newton法求解，可得

(11)

式中：R是对角矩阵。Rd的元素为

Rd,i,i=

(12)

式中：p表示所使用范数的阶次；ε是一个极小的数，用以保证di-fi-1-Ji,jΔmi→0； 矩阵Rd是非奇异的；Rm与Rd具有相似的形式，其元素为

Rm,i,i=

(13)

式(11)写成通用形式

(14)

在求解地球物理反演问题时，以Lp范数(p≥1)作为测度进行解的估计，根据观测数据和模型参数的统计特征，使用不同的范数。如果实际地下电阻率平滑地渐变，测量误差服从高斯分布，L2范数是最合适的方法，它对每一个元素进行平方，将向量的L2范数最小化，在数据拟合时，剔除相邻单元的异常值，空间区域之间无明显边界，排除了空间结构的突变。但在实际地质结构中，如煤层、金属矿山等的边界会出现明显的突变，此时，需要采用L1范数求解，它对模型电阻率值的绝对值变化最小化，对误差大的数据不敏感，保留了相邻元素之间的异常值。

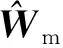
4 约束条件

对于迭代重加权最小二乘法，每次迭代的权函数均不相同，为了在重加权函数中施加先验约束信息，定义结构度量方程[19]

X=|mi-mt|

(15)

式中，与L1范数不同，mt在不同约束信息下代表不同的模型信息，例如相邻单元的电导率、常数电导率等。引入关于X的重加权函数Wf，根据不同的约束要求，Wf可以用不同的函数替代。本文选择互补误差函数Wf1或误差函数Wf2

(16)

(17)

式中：M是重加权的权重均值；S是权重标准偏差。重加权函数是一个基于正态的累积分布函数，其目的是在X变化时，施加不同的权重。Wf1、Wf2随X的变化如图1所示。

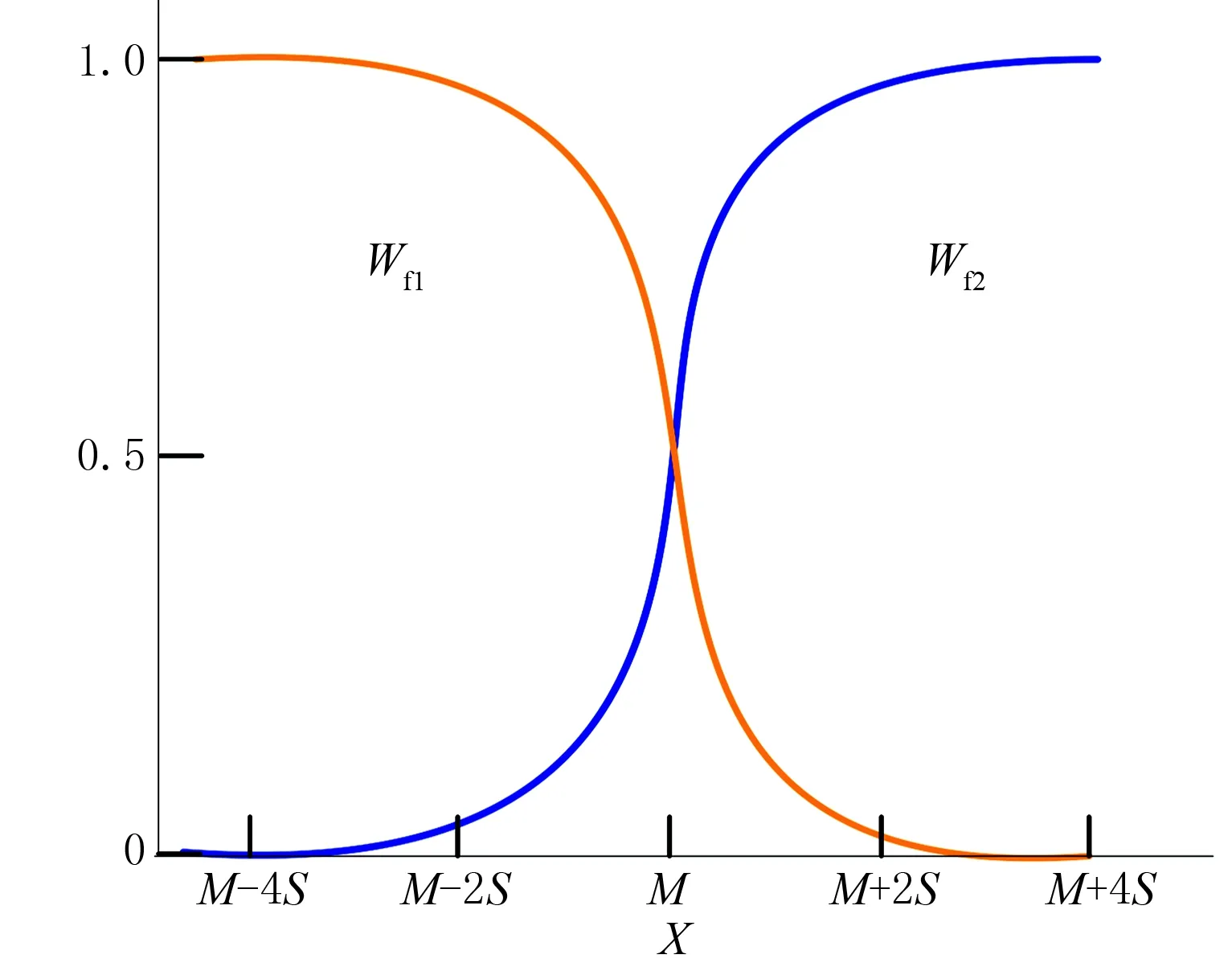
图1 权重函数曲线

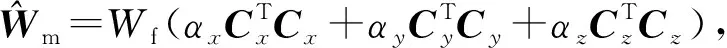
(1)L2范数平滑约束：mt代表相邻单元的电导率，选择Wf1，取一个较大的M值和较小的S值，当每个单元与相邻单元的电导率差异减小且小于M+2S时，则加权函数施加权重；当电导率差异小于M-2S时，则施加满权，使X最小化。此时的约束鼓励两个相邻单元的电导率接近，等效于L2范数施加在模型空间。

(2)L1范数块状约束：mt代表相邻单元的电导率，选择Wf1，取一个较小的M值和较大的S值，此时，当每个单元与相邻单元的电导率之差增加时，施加在相邻单元的电导率平滑约束值减少； 当二者的差异大于M+2S时，平滑约束被移除。这样，相邻单元的电导率差异被保留，两个单元的电导率值之间形成明显边界，等效于L1范数施加在模型空间。

(3)电导率极值约束：通过地质勘探等手段获取地下电导率最大值和最小值的合理范围时，反演可以施加电导率极值约束。mt代表电导率的极限值，选择Wf1，设定M=0和一个较小的S值。此时将每个单元的电导率与mt的差值作为约束，当X小于M-2S时，权重函数提供满权以最小化X；当X大于M+2S时，权重函数为0，移除约束，这使得反演结果中的元素电导率的最小值为mt。同样，如果选择Wf2，则反演结果中的元素电导率的最大值为mt。

在已知勘探区域的电阻率极大值和极小值、区域断面位置和地下空间结构等信息的条件下，可将反演区域分为若干子区域，通过修改重加权函数的参数，增加、减少或改变每个子区域的约束信息，提高反演精度。

5 反演方法

共轭梯度法是一种常用的地球物理反演优化算法，在求解式(14)时，采用并行共轭梯度最小二乘法(Parallel Conjugate-Gradient Least-Squares,PCGLS)[12]。该方法将处理器分为主处理器和多个从处理器，反演时由主处理器分配任务给不同的从处理器，自身也同时执行计算数据量较小的任务，待从处理器完成计算任务后，主处理器再分配下一次计算任务，主、从处理器协同工作，达到提高计算效率的目的，IRLS反演流程见图2。令式(14)的右侧为b，设PCGLS的内迭代次数为j=0，1，2，…，n，λ(j)为Δm的修正因子，γ(j)是b的修正因子，数据拟合的条件是测量数据与模拟数据之间的均方误差小于设定的容许值，算法收敛的条件是满足数据拟合，或者内部迭代次数j达到预设值。

图2 IRLS法迭代流程

6 合成数据反演实例

6.1 三维模型

为了评价最小二乘法三维电阻率反演效果，利用合成数据进行三维反演。应用有限元法，由TetGen软件建立四面体非结构网格三维模型，并采用局部加密的方式，减少网格数量，提高网格精度。三维模型如图3a所示，四面体模型由三角形网格构成，有限元空间定义为800m×800m×500m，监测区尺寸为16m×12m×10m，内部设有两个2m×2m×2m的低阻异常体，其中低阻块1的电导率为0.020S/m，低阻块2的电导率为0.200S/m，围岩电导率为0.002S/m，低阻块埋深均为1m。测区布置3条测线，共48个电极，电极距为1.0m，测线间距为5.5m，电极分布和剖面位置见图3b和图3c。生成的合成数据引入5%高斯噪声。

图3 合成模型(a)三维模型示意图； (b)模型水平截面图； (c)模型y=0切面图

为了对比混合约束条件下先验信息的效果，分别采用平滑约束、块状约束和混合约束对该模型进行反演，比较不同约束信息下的反演结果。计算机CPU为 Intel i5-3470，主频为3.2G，内存为16GB，模型网格信息见表1。

有限元正演过程采用预条件共轭梯度法计算刚度矩阵，求解空间的电场分布[7,23]。

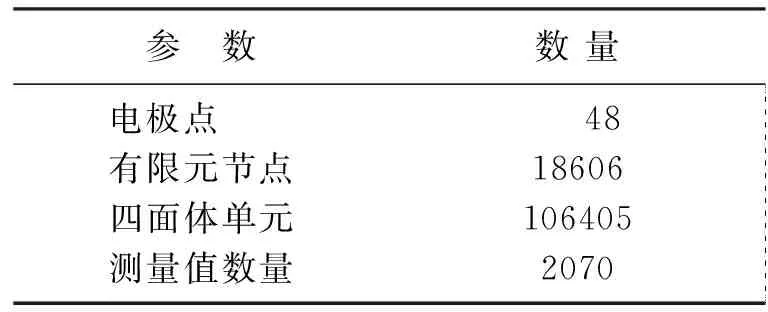
表1 模型参数信息表

6.2 不同先验信息约束的反演

6.2.1 平滑约束反演

对测区使用平滑约束反演。结构度量中，mt代表相邻单元的电导率，选择Wf1，设M=10，标准偏差S=0.1，测区及低阻块采用同样的约束规则。反演结果如图4所示，可见在平滑约束下，反演结果中低阻异常体的位置基本正确，但反演精度较低，电导率从低阻的中心位置向围岩逐渐降低，地质结构具有平滑过渡的特征；在低阻块2中，反演低阻区域形态与模型不完全一致，低阻区向测线位置延伸。

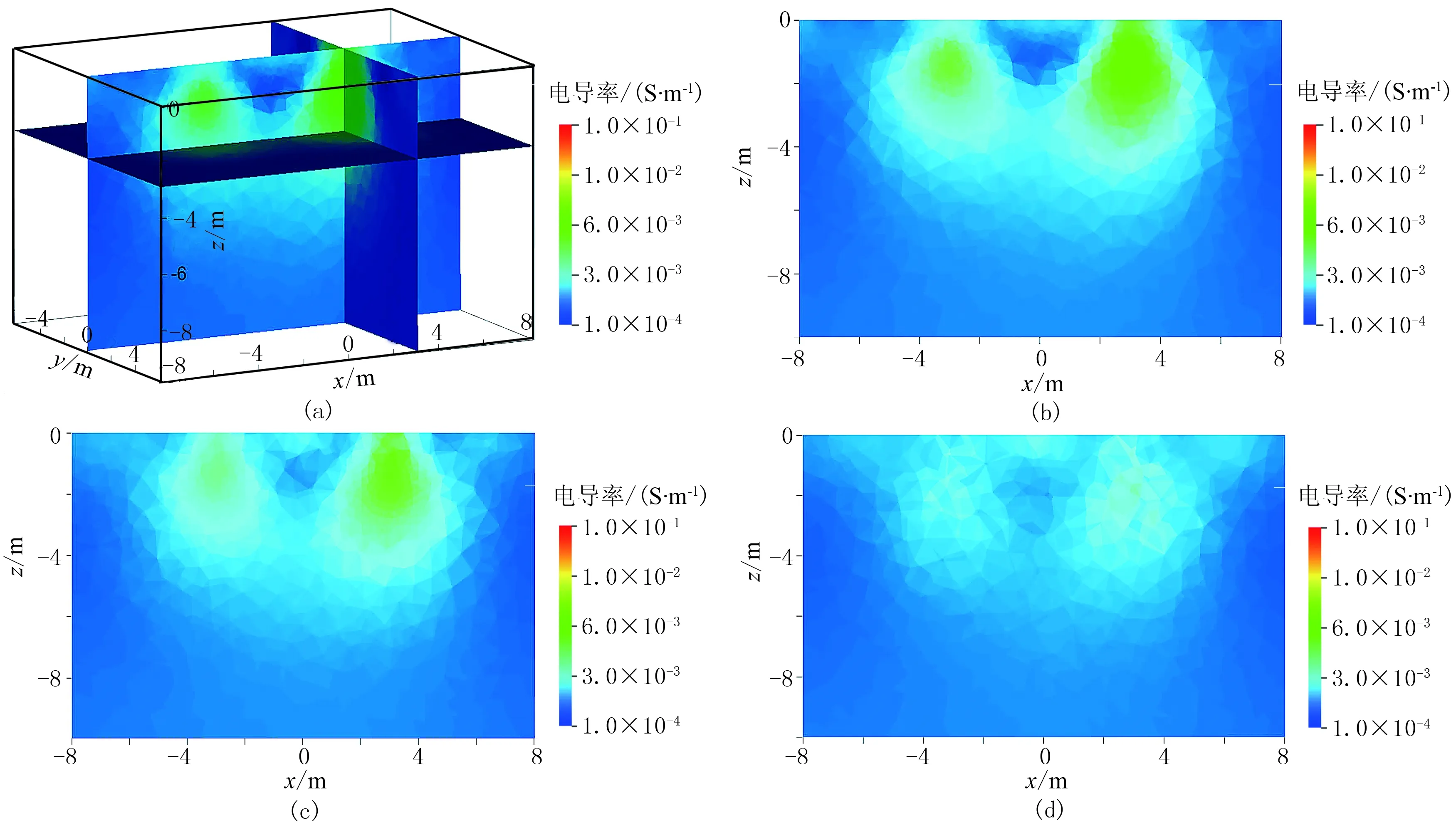
图4 平滑约束反演结果(a)三维切片； (b)y=0切片； (c)y=1m切片； (d)y=2m切片

6.2.2 块状约束反演

对测区及低阻块施加块状约束反演(非连续地质结构反演)，仍采用函数Wf1，结构度量中mt代表相邻单元的电导率，约束信息的施加通过减小权重函数的均值实现。取值M=0.1、S=0.01时的反演结果如图5所示，可以看出，M值减小后，反演时会移除更多的相似约束，导致相邻单元的电导率呈现较大差异，反演结果中低阻异常体位置基本准确，但精度不够。与地质原型相比，形态出现较大偏差，低阻块2表现得尤为明显，同时低阻块1和低阻块2向测线位置偏移。

从图4和图5的反演结果可以看出，单纯采用平滑约束(L2范数)或者块状约束(L1范数)的反演精度均不够理想。在工程实践中，由于测量误差和人工操作的影响，反演结果的精度会更低。

6.2.3 混合约束1反演

对测区和低阻块同时施加平滑约束、最大值约束、最小值约束进行反演(称为混合约束1)，对测区和低阻块分别施加约束值。考虑实际地质结构中，同一块地质单元电导率可能会有变化，甚至可能出现数倍的差异，因此设定某区域电导率最大值和最小值时，保留较大的余量。对每个区域同时施加三个约束条件，以测区为例，施加约束信息为：①对于平滑约束，mt代表相邻单元的电导率，选择Wf1，设定M=10，S=0.1； ②对于最大电导率值约束，设定mt=0.01S/m，选择Wf1，M=0，S=0.1；③对于最小电导率值约束，设定mt=0.0004S/m，选择Wf2，M=0，S=0.1。对低阻块1和低阻块2，同样施加平滑约束和电导率极值约束信息，其中低阻块1最大电导率值mt=0.1S/m，最小电导率值mt=0.004S/m；对于低阻块2，设定最大电导率值mt=1.0S/m，最小电导率值mt=0.04S/m。三种约束信息同时施加的反演结果如图6所示，可以看出，施加多个约束信息后，反演结果的精度有较大的提高，反演的测区电导率值较接近于理论模型，其中最大电导率σmax=0.03705S/m，最小电导率σmin=0.001209S/m，低阻块的位置形态与理论模型基本一致。需要说明的是，对低阻块2施加电导率极值约束(0.04S/m≤σ≤1.00S/m)后，实际上该区域电导率接近0.04S/m，在图例中接近红色区域，因此视觉上像是一个红色方块。

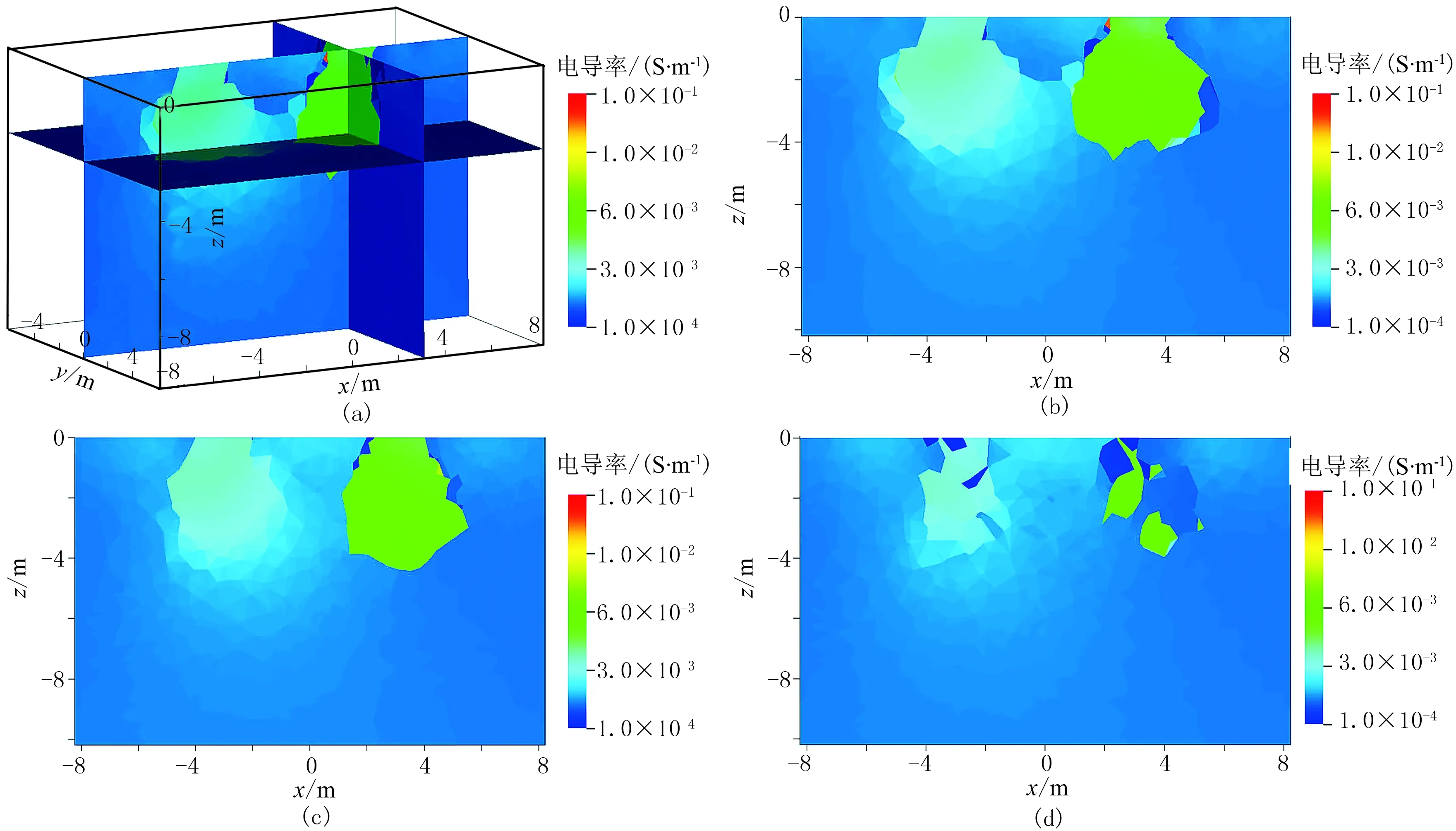
图5 非连续地质结构约束反演结果(a)三维切片； (b)y=0切片； (c)y=1m切片； (d)y=2m切片

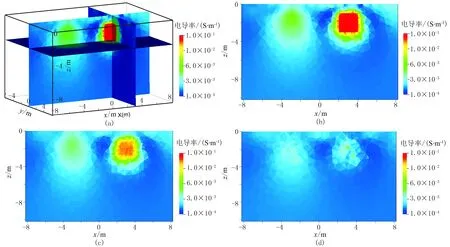
图6 混合约束1反演结果(a)三维切片； (b)y=0切片； (c)y=1m切片； (d)y=2m切片

6.2.4 混合约束2反演

对低阻块1施加平滑约束和电导率极值约束，对低阻块2施加块状约束和电导率极值约束(称为混合约束2)，方法同混合约束1，电导率极值不变。反演结果如图7所示，可以看出，对低阻块2的约束信息改为块状约束后，成像质量较好，低阻区域的位置和形态与模型高度一致。整个测区最大电导率σmax=0.04149S/m，最小电导率σmin=0.001688S/m。由于在低阻块2中施加了块状约束和电导率极值约束，反演结果中低阻块2边界处的电导率允许出现不连续。而在低阻块2内部，电导率极值的约束条件为0.04S/m≤σ≤1.0S/m，反演得到该区域电导率为0.04～0.04149S/m，因此低阻块2呈现单独的块状形态。与低阻块1所施加的平滑约束相比，在不连续地质结构中，块状约束可以更好地反映地质体的结构变化，这在矿产资源的勘探和开采监测中尤其重要。

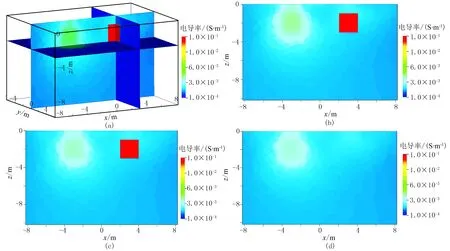
图7 混合约束2反演结果(a)三维切片； (b)y=0m切片； (c)y=0.99m切片； (d)y=1.1m切片

6.3 不同约束下PCGLS法计算效率

施加不同约束信息时，PCGLS法反演性能数据统计见表2。合成算例中PCGLS算法计算时间在数分钟至数十分钟以内，与文献[16](约160min)、文献[5](约86min)的方法相比，计算速度得到较大提高。不同约束信息对迭代次数和运行时间有较大的影响，从表2可见，混合约束2反演效果优于混合约束1，且迭代次数和运行时间更少，因此在施加反演约束信息时，应根据地质条件合理施加。图8给出了迭代过程中数据失配数量变化，迭代中第一个值为起始模型的数据失配数量。迭代过程中，最大数据失配数量为54个，不超过总数据量的2.6%。拟合均方根误差(RMSE)为最后一次迭代后的结果，平滑约束和混合约束1由于采用了平滑约束，地质结构更加光滑，反演结果中(自然对数)电导率数据与测量数据偏差较大，均方根误差大于1.5；而采用块状约束时，反演允许相邻单元的电导率出现较大差异，保留较多的原始数据，因此拟合均方根误差相对较小。

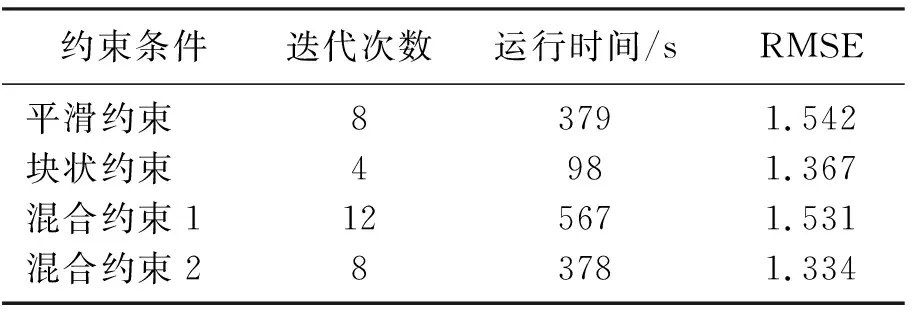
表2 不同约束信息的迭代次数和运行时间统计表

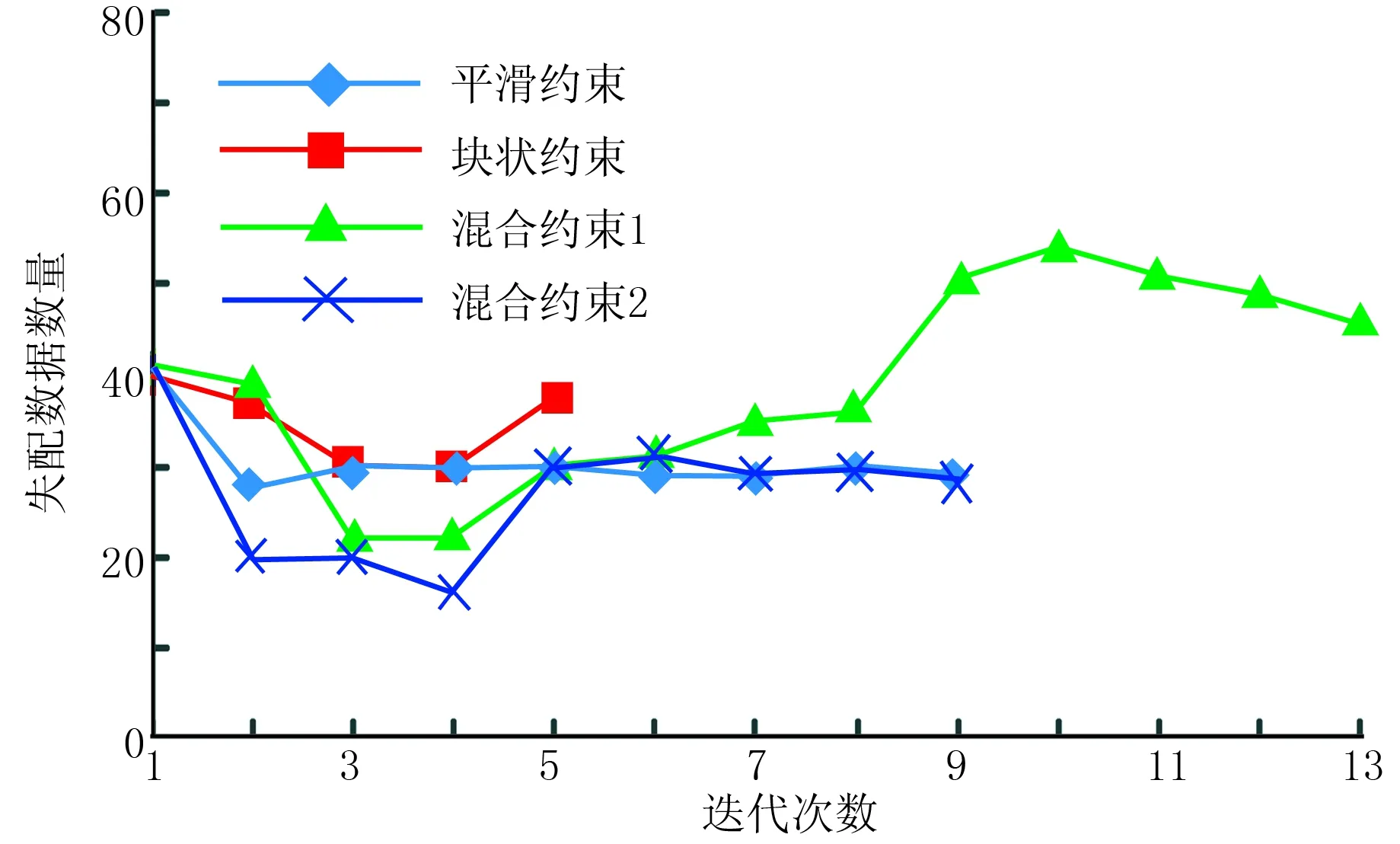
图8 迭代过程中的数据失配数量

7 结论

基于迭代重加权最小二乘法实现三维电阻率反演时，将数据加权矩阵中的重加权函数修改为误差函数和互补误差函数的形式，通过对重加权函数参数做简单改动，达到不同先验信息约束的效果；反演过程中，主、从处理器多线程协同工作，共同完成反演迭代流程。合成数据的成像结果证明该方法的有效性，与单一信息约束的反演对比说明，合理施加多信息约束可以提高成像结果中异常体位置和形态的准确性；与同类型算法相比，反演耗时较短，有助于提高三维电阻率层析成像的时效。

结合其他勘探手段，获得更多的地质结构信息，是提高直流电法三维成像效果的重要途径，对所述方法进行工程验证，并进一步挖掘测量数据的价值，是后续研究的重点。